Svar på opgave 1:

1. Hældningen til tangenten for grafen, når x = 1 er lig med f'(1). Man differentierer f(x) og får: f'(x) = -3x² + 8x - 3. f'(1) = -3(1)² + 8(1) - 3 = -3 + 8 - 3 = 2

Svar på opgave 2:

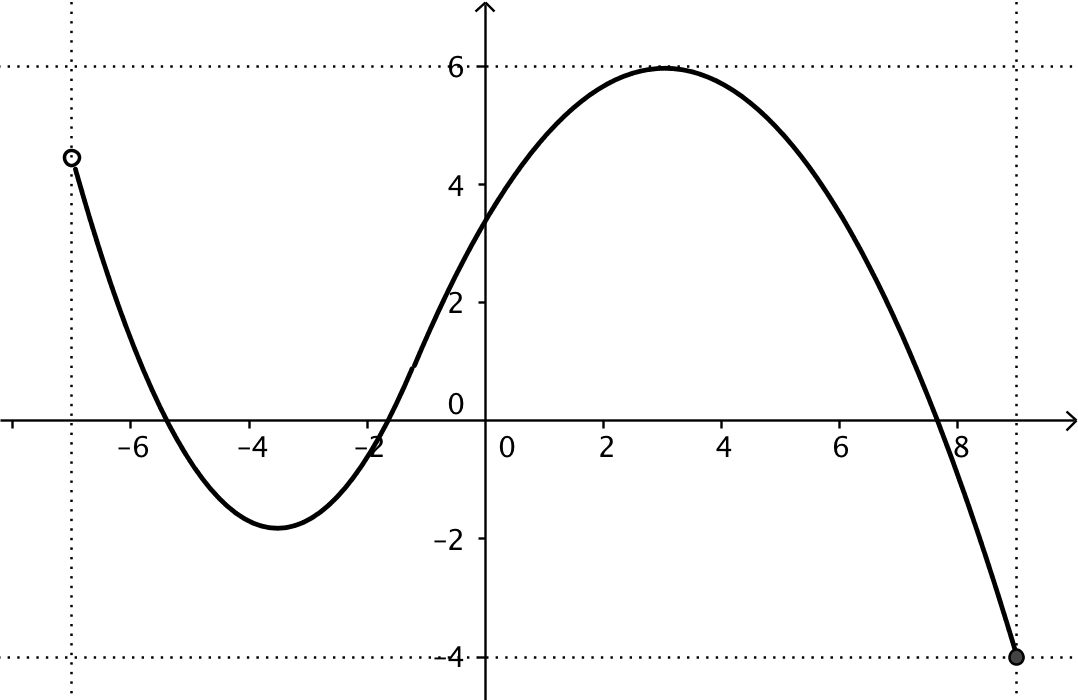
1. Tre nulpunkter betyder, at grafen skærer x-aksen tre steder. f'(3) = 0, betyder at der er vandret tanget for x = 3. Her er valgt, at der skal være maksimum.

   Dm(f) er definitionsmængden, dvs. det interval som x tilhører. Vm(f) er det interval, som f(x) ligger i. Disse intervaller er markeret med stiplede linjer.

   Den åbne cirkel for x = -7 betyder, at dette punkt ikke hører med til grafen, mens det lukkede punkt for x = 9 betyder, at punktet hører med.

   

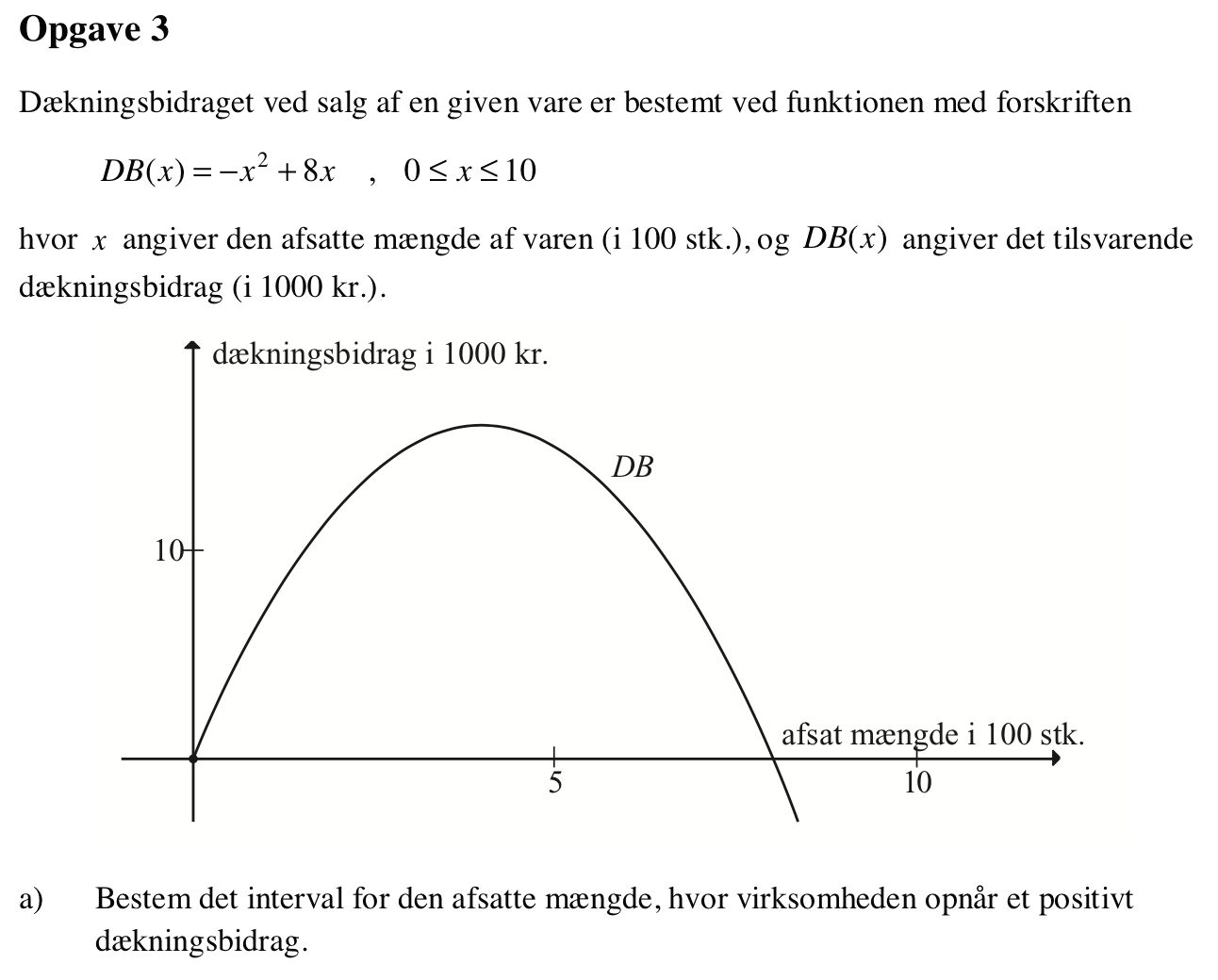
Svar på opgave 3:

1. Man skal løse ligningen DB(x) = 0, hvor 0 ≤ x ≤ 10. Man får

   DB(x) = 0 ⇒ -x² + 8x = 0 ⇔ x·(-x + 8) = 0 ⇔ x = 0 ∨ x = 8. Intervallet bliver derfor: x ∈ [0;8]

Svar på opgave 4:

1. Man skal finde integralet:

   

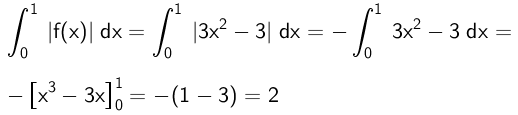
   Dvs. arealet er 2

   Man kan også bruge formlen for arealet af en parabel med grundlinjen 2 og højden 3: (2/3)·2·3 = 4. Af dette tager man det halve og får arealet 2.

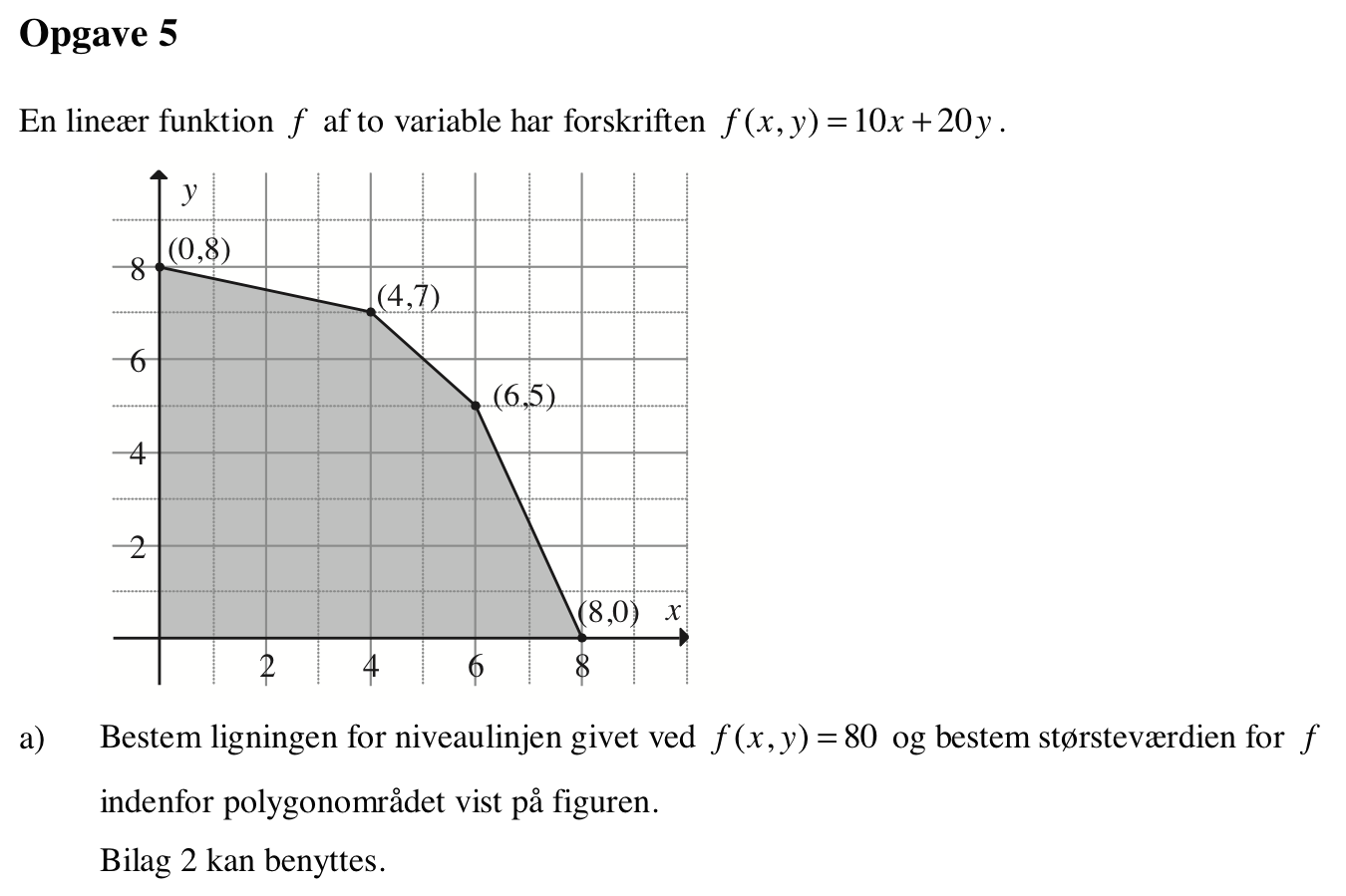
Svar på opgave 5:

1. f(x,y) = 80 = 10x + 20y ⇒ y = -0,5x + 4

   

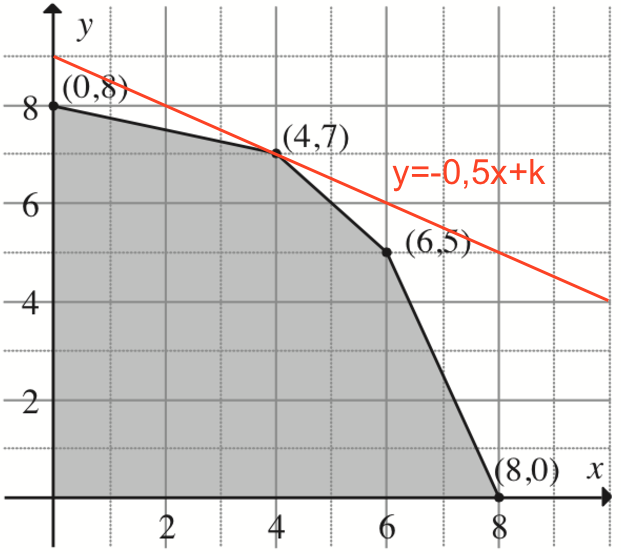
   Det ses af figuren, at maksimum antages i punktet (x,y) = (4,7). Man paralleforskyder en linje parallel med y=-0,5x+4, så den kommer så langt væk fra (0,0) som muligt samtidig med, at den har mindst et punkt tilfælles med polygonområdet.

   Maksimum er derfor f(4,7) = 10·4 + 20·7 = 40 + 140 = 180

Svar på opgave 6:

1. Isolering af Y:

   

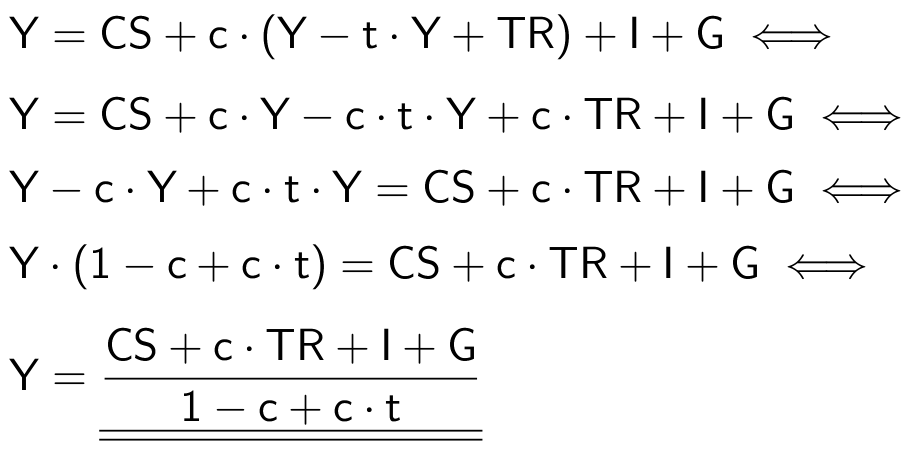
2. 2. Ligningen faktoriseres

   3. Man bruger nulreglen til at dele op i to under-ligninger

   4. I første ligning isoleres x. I anden ligning isoleres eksponentialfunktionen indeholdende x

   5. I anden ligning tager man ln() på begge sider af lighedstegnet

   6. I anden ligning isoleres x. Den samlede løsning er x = -3 eller x = 0.

Svar på opgave 7:

1. Man skal finde P(X < 490) og bruger Ti-Nspire kommandoen normCdf(−∞,490,500,10), der giver: P(X < 490) = 0.1587 = 15,9 %

2. Man starter med at dele datasættet op i grupper á 10 gram startende med 470 og afsluttende med 530. Man tæller antallet af rejer i hver gruppe, beregner de summerede frekvenser og får følgende diagram for vægtfordelingen:

   

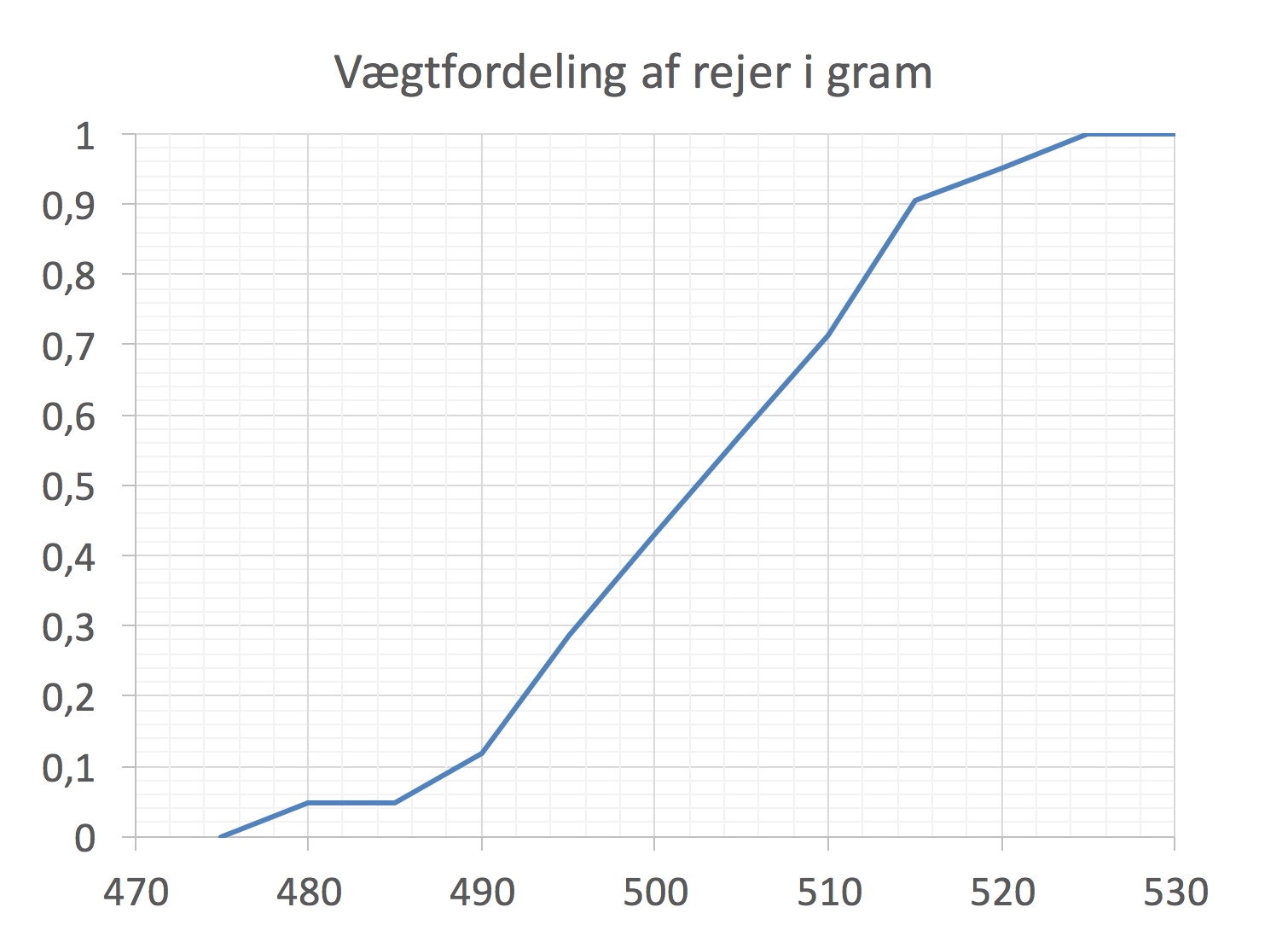
3. Man bruger Excel til at finde forskellige deskriptorer og kvartilsæt.

   

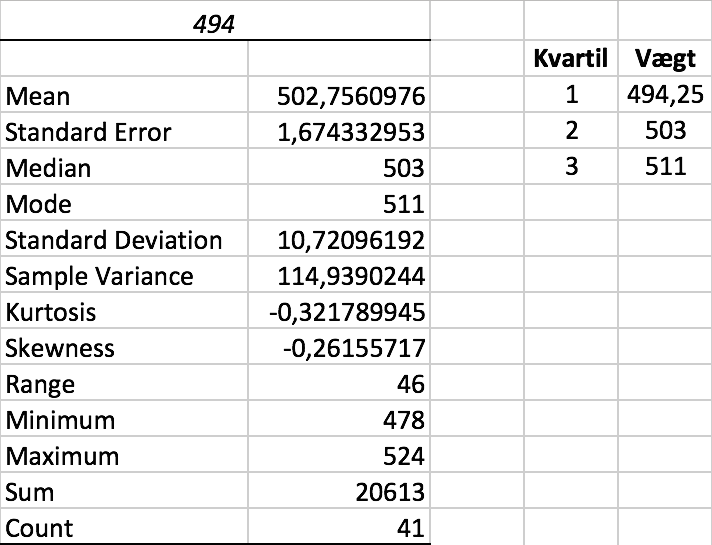
   Kvartilsættet: 1. kvartil: 495, median: 503, 3. kvartil: 512. Typetallet (mode) = 511. Middelværdien (mean) = 502 og variansen er 111.

   Man skal bruge programmet Dataanalyse. I Excel 2016 installeres programmet ved at gå ind i Funktioner > Excel tilføjelsesprogrammer... og sætte hak i Analysis ToolPak og trykke OK.

   Derefter går man ind under Data > Dataanalyse > Descriptive Statistics. Dette er vist nedenfor:

   Se Excel beregninger i filen Rejer

Svar på opgave 8:

1. Funktionen er analyseret med nedenstående kommandoer 1-7) i Ti-Nspire:

   

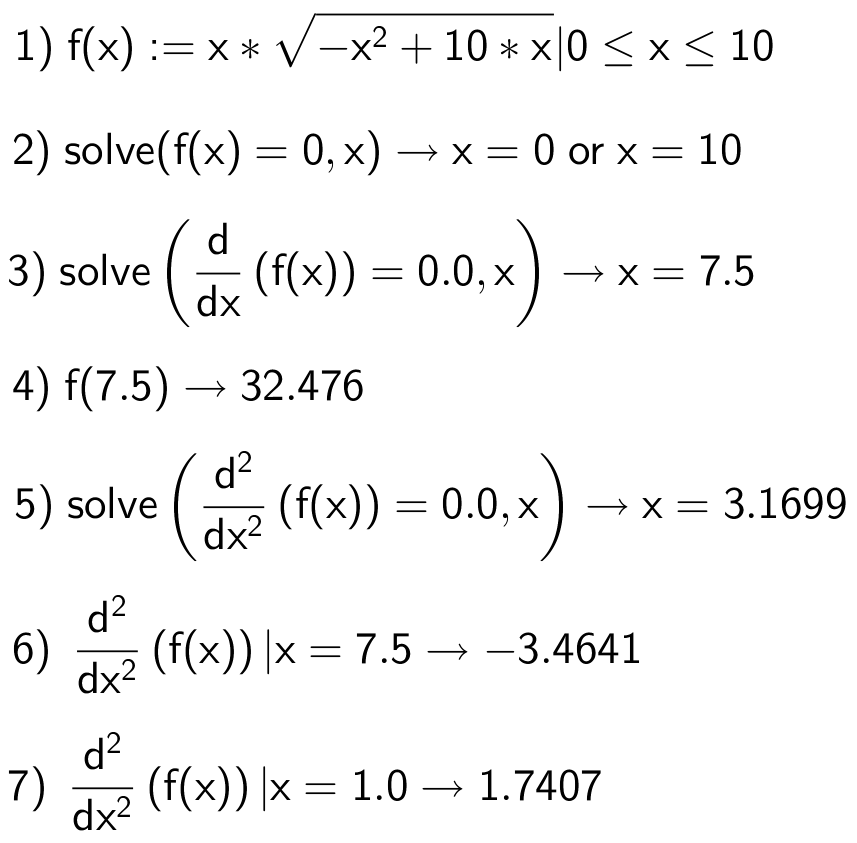
   1) funktionen defineres

   2) nulpunkterne findes for funktionen, der er: x = 0 og x = 10. Da x ≥ 0 og kvadratrodsdelen af funktionen ligeledes kun kan antage værdier ≥ 0 vil f(x) være ≥ 0 for alle x i definitionsmængden.

   3) Nulpunkterne for f'(x) findes. Dette giver, at f'(x) = 0 for x = 7,5. Da f(x) ≥ 0 og kun 0 i endepunkterne, er x = 7,5 et maksimum. Funktionen er dermed voksende for x < 7,5 og aftagende for x > 7,5.

   4) Maksimum af funktionen er 32,48

   5) Nulpunkterne for den anden-afledede af funktionen findes. Man får at f''(x) er 0 for x = 3,17. I dette punkt har funktionen vendetangent.

   6) - 7) Værdien af den andenafledede findes for to x-værdier; en på hver side af vendetangenten. Til venstre for vendetangenten er f''(x) > 0 og dermed opadhul (glad) eller konveks; omvendt er f''(x) < 0 til højre for vendetangenten og dermed nedadhul (sur) eller konkav.

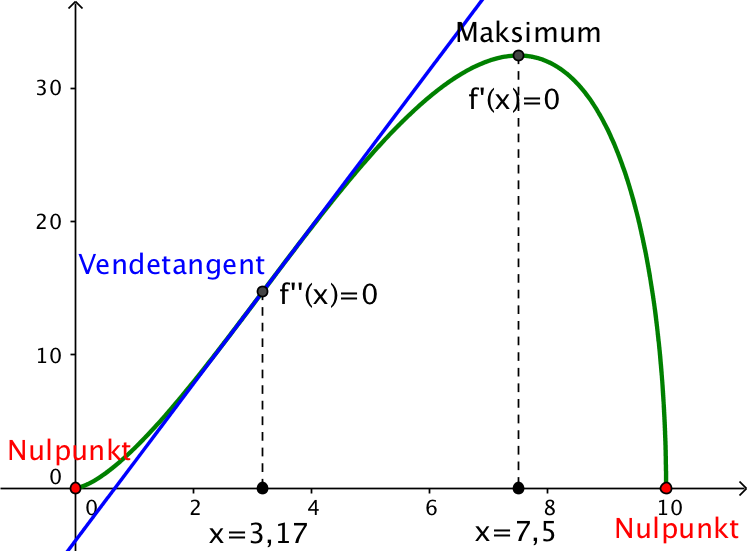
2. Grafen for f er grøn og lavet i Geogebra.

   

Svar på opgave 9:

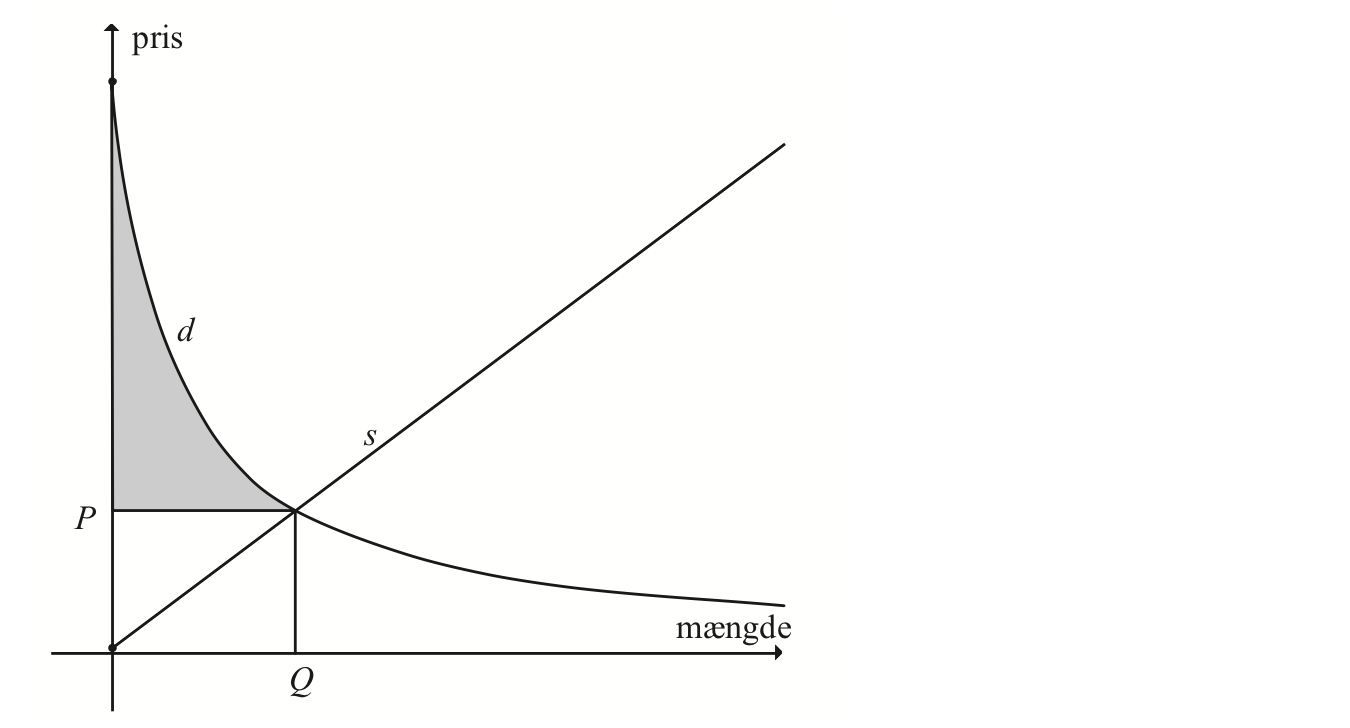
1. Man får:

   

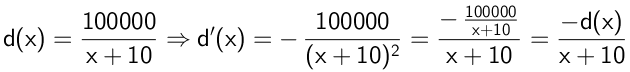
   der viser at d(x) er en løsning. Desuden opfylder d(x) startbetingelsen, idet d(0) = 100.000/10 = 10.000.

2. Man skal løse ligningen d(x) = s(x) og gør det med TiNspire kommandoen:

   

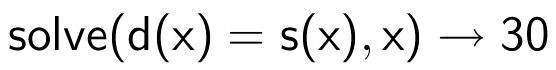
   Dernæst skal man finde d(30) = 2500. Dvs. svaret er: ligevægtsmængden er 30 og ligevægtsprisen er 2500 kr.

3. Arealet er integralet af d(x) - 2500 fra x = 0 til x = 30. Man får:

   

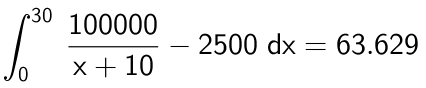
   Dvs. forbrugeroverskuddet er 63.629 kr.

Svar på opgave 10:

1. Den lineære regressionslinje er fundet i Excel og vist på figuren nedenunder.

   

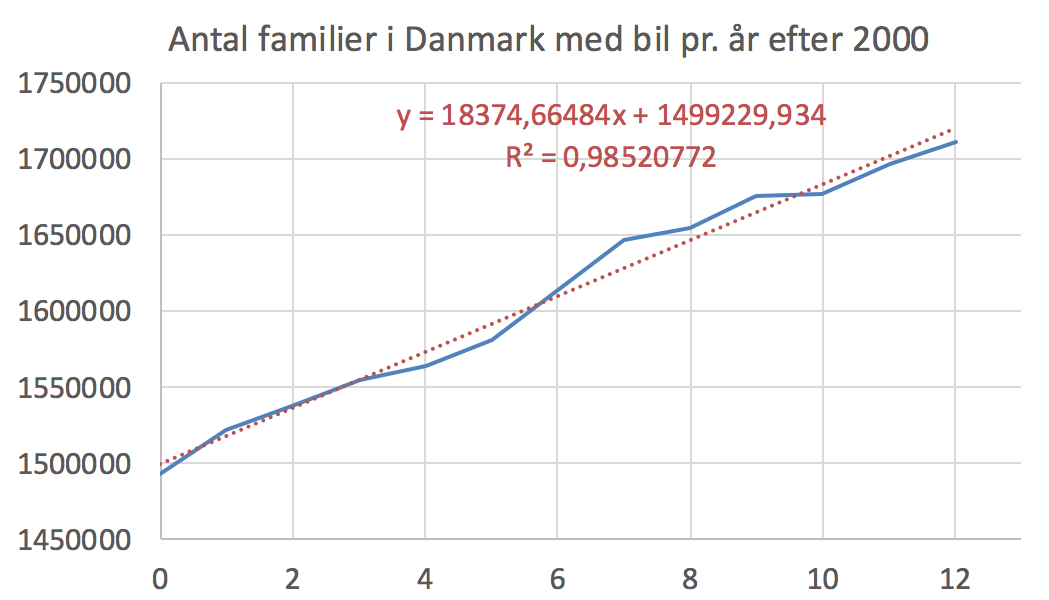
   B(x) = 18.375·x + 1.499.000

   (Se figuren nedenunder for mere præcise værdier af hældning og skæring med y-aksen under "Koefficienter").

2. Konfidens-intervallet for hældningen er beregnet i Excel og vist på figuren nedenunder.

   Man skal bruge programmet Dataanalyse. I Excel 2016 installeres programmet ved at gå ind i Funktioner > Excel tilføjelsesprogrammer... og sætte hak i Analysis ToolPak og trykke OK. Derefter går man ind under Data > Dataanalyse > Regression.)

   

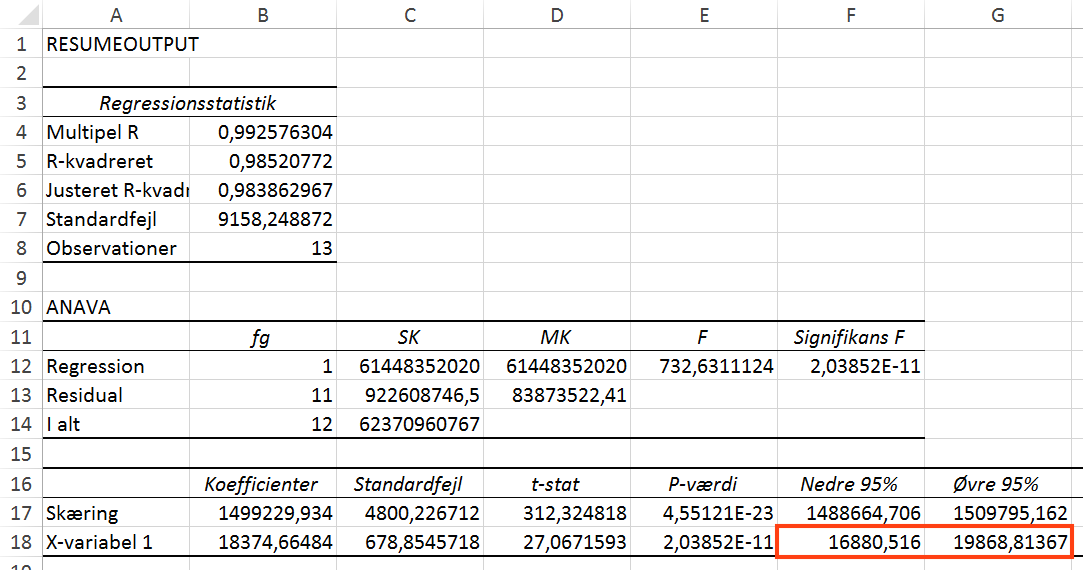
   Det fremgår at intervallet er [16.881;19.869]

3. Den årlige stigning på 17.000 er lavere end den fundne hældning på regressions-kurven, men den ligger i 95% konfidensintervallet. Oplysningen om, at antallet af biler samlet er steget med 220.000, passer med den observerede stigning på 218.397, når man runder af til nærmeste antal 10.000.

Se beregninger i Excelfilen Familier

Svar på opgave 11:

1. DB(x,y) = DB(x) + DB(y) = x·(p(x) - 100) + y·(q(y) - 100) = x·(-0,2x + 700 - 100) + y·(-0,25y + 900 - 100) = -0,2x² + 600x - 0,25y² + 800y.

2. DB(x,y) har formen ax² + bx + cy² + d. Da a og c har samme fortegn, er niveau-kurverne ellipser.

3. DB(x,y) = ax² + bx + cy² + d. Da a og c er negative, er optimumspunktet et maksimum for dækningsbidraget. Det optimale salg af ERGO kaldes x_o og det optimale salg af FLEX kaldes y_o. Der gælder at

   x_o = (-b/(2·a)) = (-600/(-2·0,2)) = 1.500 stk. og y_o = (-d/(2·c)) = (-800/(-2·0,25)) = 1.600 stk.

   Dvs. det maksimale dækningsbidrag er -a·(x_o)² -c·(y_o)² = -(-0,2)·1500² - (-0,25)·1600² = 1.090.000 kr., som fås ved produktion af 1.500 ERGO og 1.600 FLEX

Opgave b) løst med Excel Problemløser:

Problemløser installeres med: Funktioner > Excel-tilføjelsesprogrammer > Solver Add In.

Se beregninger i Excelfilen Optimering

Svar på opgave 12a:

1. Ud fra besøgsdata udregnes tallen observeret

   

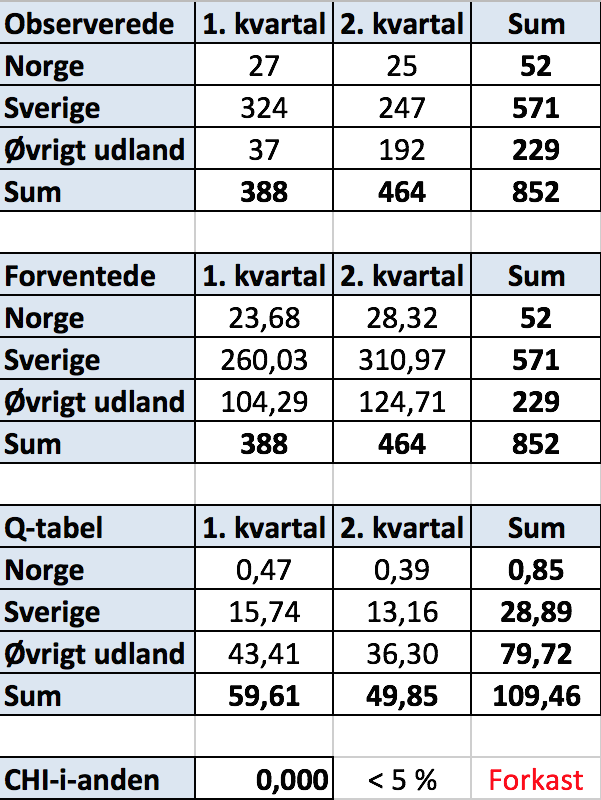
2. Nulhypotesen er, at det kvartal, som man kommer, ikke afhænger af, hvilket land man kommer fra. Tabellen "Forventede" er lavet ud fra "Observerede" ved at gange summen under et felt med summen til højre for feltet og dividere med den samlede sum 852. På grundlag af denne tabel er tabellen "Q-tabel" fremstillet. Den viser Q-værdien 109 i nederste højre felt.

   Sandsynlighden for at en Chi-i-anden fordelt stokastisk variabel (med 2 frihedsgrader) er større end eller lig med dette tal er 0,000 (med tre decimalers nøjagtighed), hvilket er mindre end 5%, og nulhypotesen forkastes dermed.

Se beregninger i Excelfilen Ekspeditioner

Svar på opgave 12b:

1. Hun låner 40%·840.000 kr. = 336.000 kr. Ydelsen (i forbindelse med gældsannuitet) bliver:

   

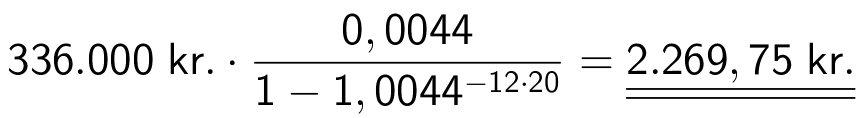
2. Restgælden efter 10 år (120 terminer) bliver:

   

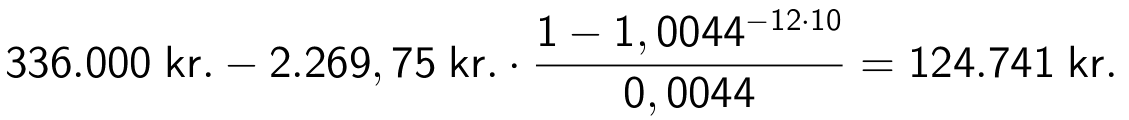
   Da dette beløb er mindre end 200.000 kr. gælder, at arven er stor nok til at betale restgælden.

Svar på opgave 12c:

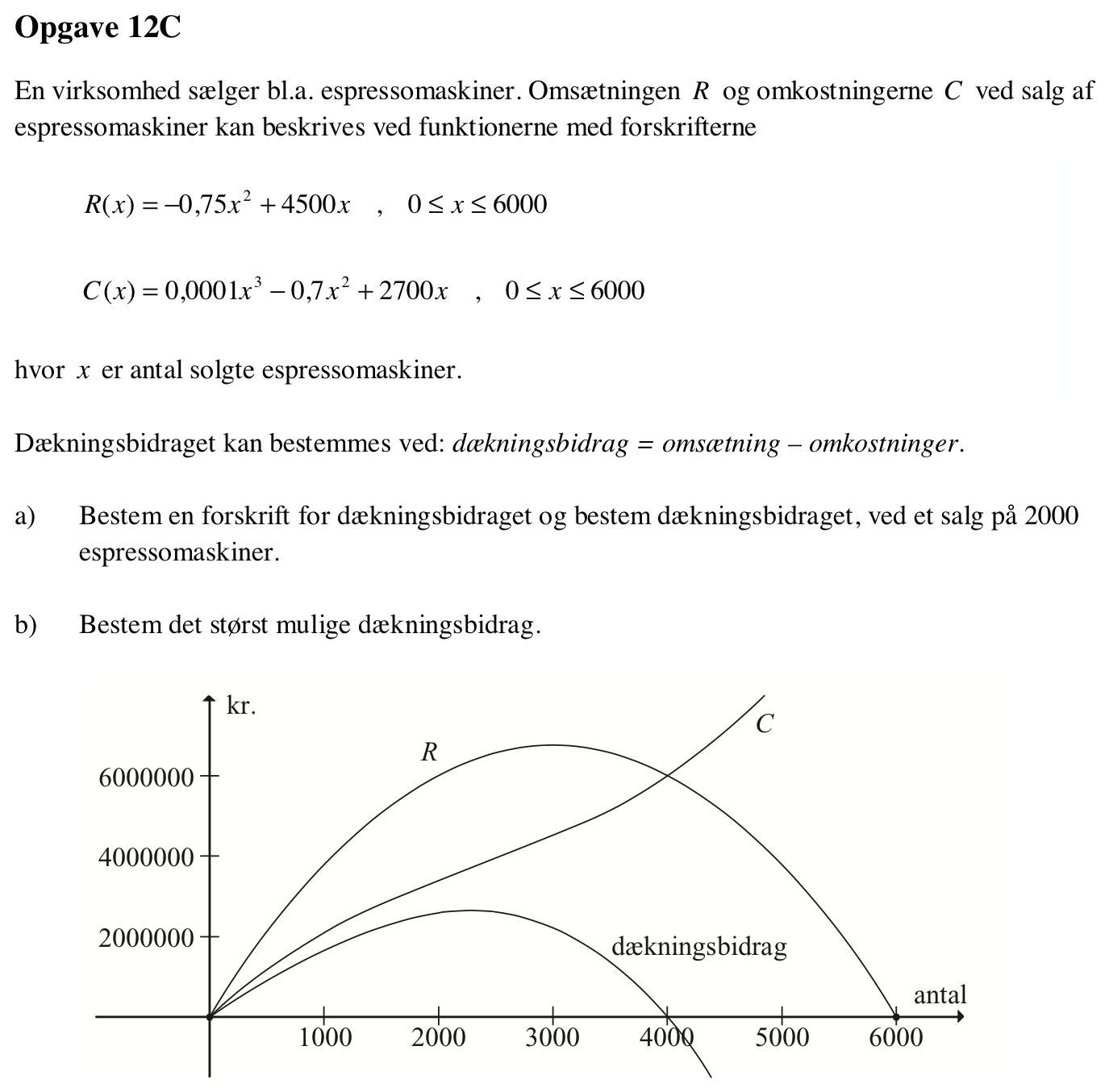
1. Dækningsbidrag kaldes D(x). D(x) = R(x) - C(x) = −0,0001x³ - 0,05x² + 1.800x

   D(2000) = −0,0001·2000³-0,05·2000²+1800·2000 kr. = 2.600.000 kr.

2. Man skal finde D'(x) = 0 for 0 ≤ x ≤ 6.000. Man bruger kommandoen i Ti-Nspire:

   

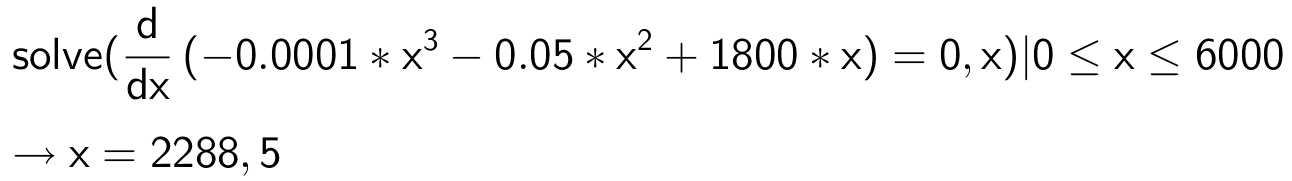
   At det er maksimum fremgår af figuren. Det giver det maksimale dækningsbidrag:

   D(2.288,5) = 2.659.000 kr.