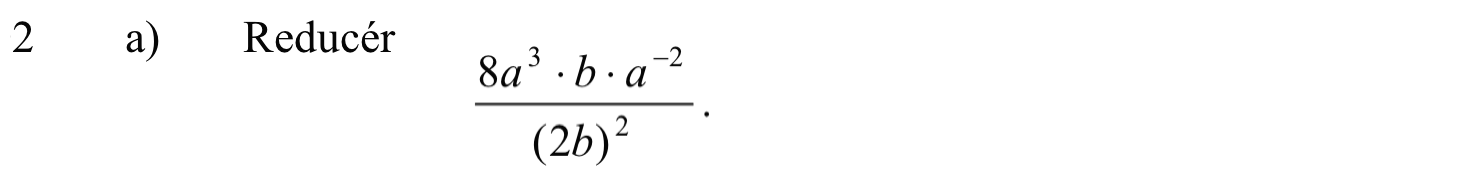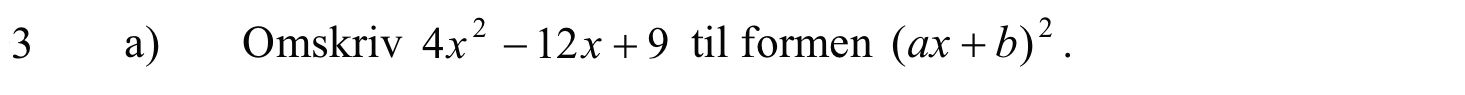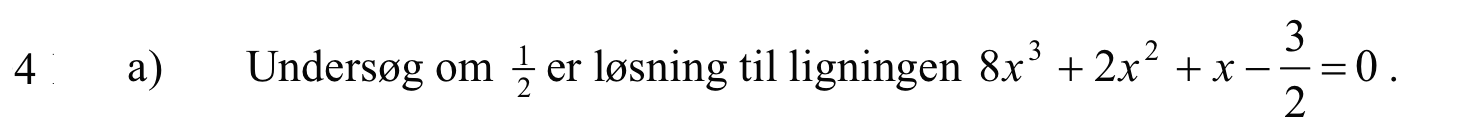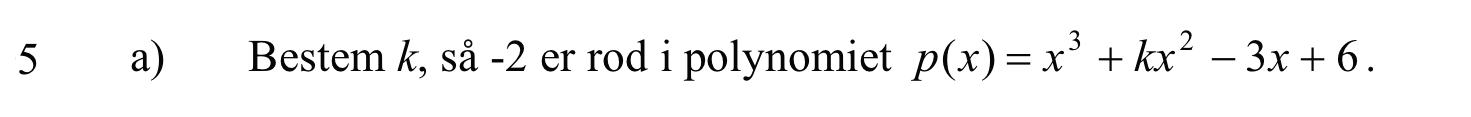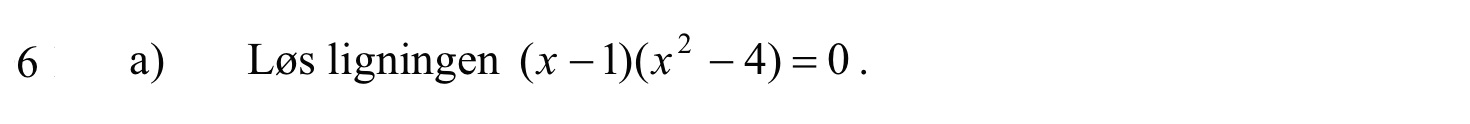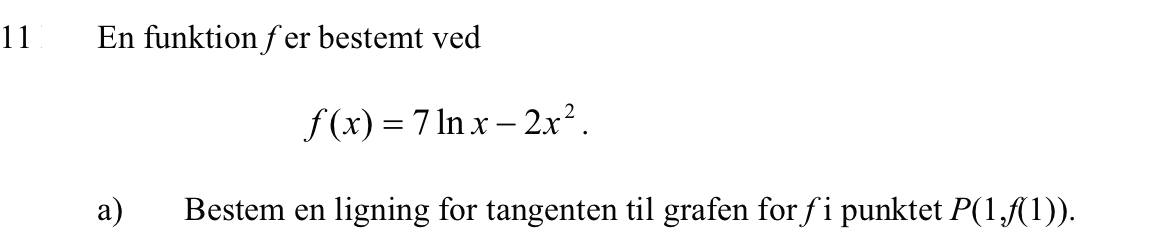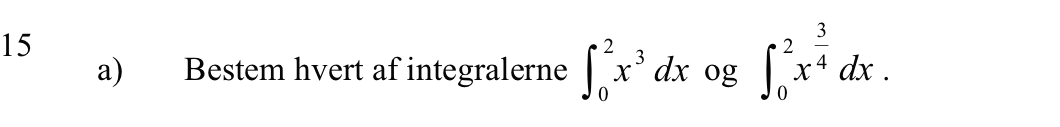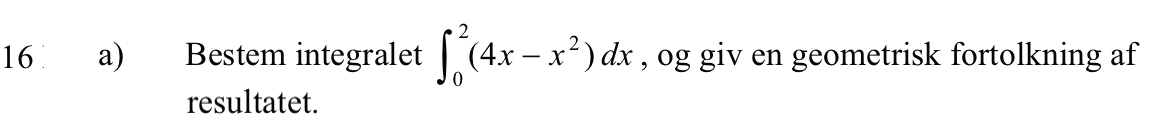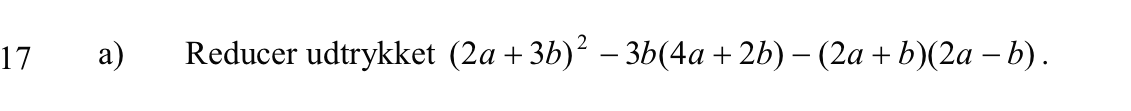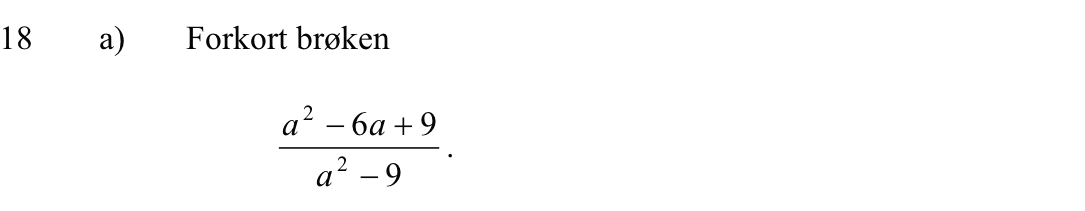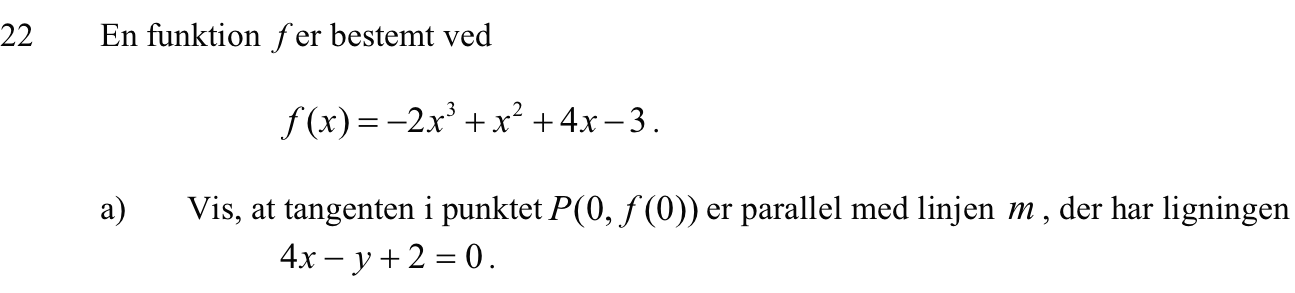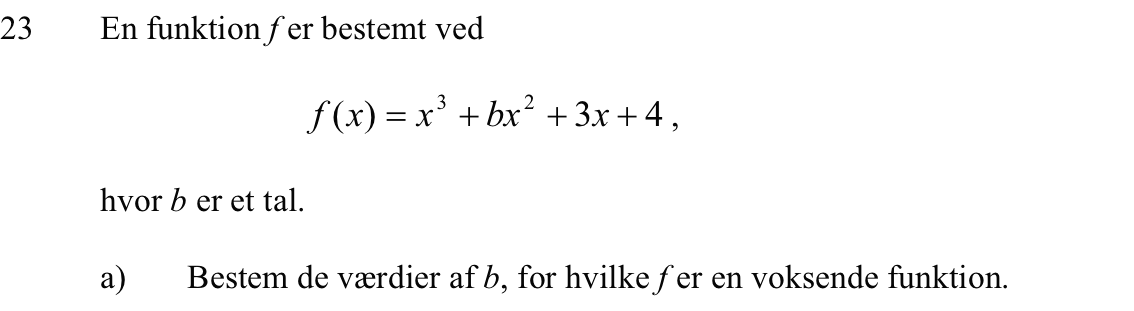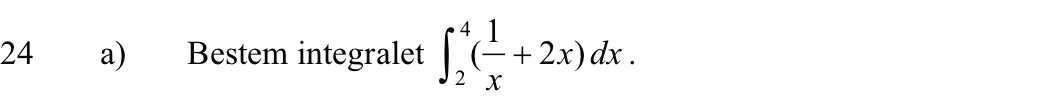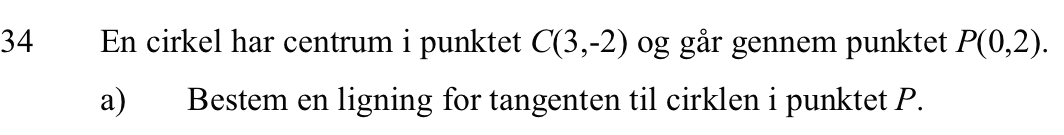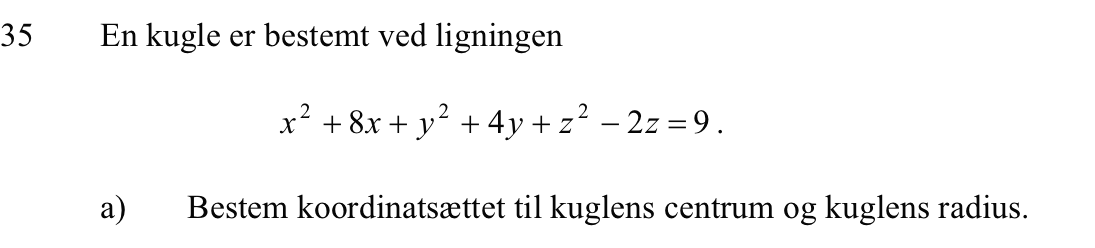De første opgaver er nye opgaver, mens de efterfølgende 40 er gamle. Klik på hver enkelt opgave for at se løsning.
Svar på opgave 1. Reducering.
-
a2 - 6·a·b + 3·(a + b)2 = 1·a2 - 6·a·b + 3·a2 + 6·a·b + 3·b2 = (1 + 3)·a2 + 3·b2 + 0·a·b = 4·a2 + 3·b2
-
(a + b)·(a - b) + 2·b2 = a2 - b2 + 2·b2 = a2 + (-1)·b2 + 2·b2 = a2 + (-1 + 2)·b2 = a2 + b2
-
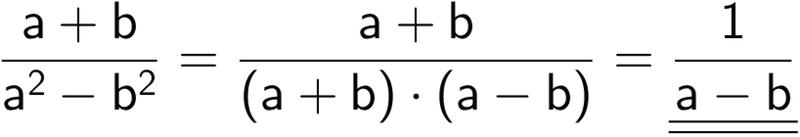
-
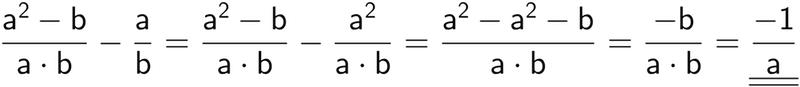
Løs følgende førstegradsligninger:
-
3·x + 6 = 4 + x
-
7 - x = 3·x + 2
-
11·x - 3 = x
Svar på opgave 2. Førstegradsligninger.
-
3·x + 6 = 4 + x ⇔
3·x - x = 4 - 6 ⇔
2·x = -2 ⇔
x = −1
-
7 - x = 3·x + 2 ⇔
-x - 3·x = 2 - 7 ⇔
-4·x = -5 ⇔
x = 5/4
-
11·x - 3 = x ⇔
11·x - x = -3 ⇔
10·x = -3 ⇔
x = -3/10
Løs følgende andengradsligninger:
-
3·x2 + 2·x = 1
-
2·x2 = -3·x
-
x2 - 4 = 0
Svar på opgave 3. Andengradsligninger.
-
Standardløsning:
3·x2 + 2·x = 1 ⇔
3·x2 + 2·x + (-1) = 0 ⇔
x = (-2 ± √[22 - 4·3·(-1)])/(2·3) ⇔
x = (-2 ± √[4 + 12])/6 ⇔
x = (-2 ± √16)/6 ⇔
x = -1/3 ± 2/3 ⇔
x = -1 ∨ x = 1/3
Prøve: x = -1
Venstre side Højre side 3·(-1)2 + 2·(-1) 1 3·1 - 2·1 1 1 1 Prøve: x = 1/3
Venstre side Højre side 3·(1/3)2 + 2·(1/3) 1 3·1/9 + 2·1/3 1 1/3 + 2/3 1 1 1 -
Standardløsning:
2·x2 = -3·x ⇔
2·x2 + 3·x + 0 = 0 ⇔
x = (-3 ± √[32 - 4·2·0])/(2·2) ⇔
x = (-3 ± √9)/4 ⇔
x = (-3 ± 3)/4 ⇔
x = -3/4 ± 3/4 ⇔
x = -3/2 ∨ x = 0
Løsning ved faktorisering og brug af nulregel:
2·x2 = -3·x ⇔
2·x2 + 3·x = 0 ⇔
x·(2·x + 3) = 0 ⇔ (x sættes udenfor parentes)
x = 0 ∨ 2·x + 3 = 0 ⇔ (nulregel)
x = -3/2 ∨ x = 0
-
Standardløsning:
x2 - 4 = 0 ⇔
1·x2 + 0·x + (-4) = 0 ⇔
x = (0 ± √[02 - 4·1·(-4)])/(2·1) ⇔
x = (±√16)/2 ⇔
x = ±4/2 ⇔
x = -2 ∨ x = 2
Løsning ved faktorisering og brug af nulregel:
x2 - 4 = 0 ⇔
(x + √4)·(x - √4) = 0 ⇔ (3. kvadratsætning)
(x + 2)·(x - 2) = 0 ⇔
x + 2 = 0 ∨ x - 2 = 0 ⇔ (nulregel)
x = -2 ∨ x = 2
Løsning ved isolering af x:
x2 - 4 = 0 ⇔
x2 = 4 ⇔
x = ±√4 ⇔
x = -2 ∨ x = 2
Løs følgende ligninger:
-
x·(x - 5) = 0
-
(x + 1)·(x - 4) = 0
-
(x + 1)·(x2 - 8·x + 12) = 0
Svar på opgave 4. Ligninger med parenteser.
Man bruger nul-reglen (a·b = 0 ⇔ a = 0 ∨ b = 0) i alle spørgsmål.
-
x·(x - 5) = 0 ⇔
x = 0 ∨ x - 5 = 0 ⇔
x = 0 ∨ x = 5
-
(x + 1)·(x - 4) = 0 ⇔
x + 1 = 0 ∨ x - 4 = 0 ⇔
x = -1 ∨ x = 4
-
(x + 1)·(x2 - 8·x + 12) = 0 ⇔
x + 1 = 0 ∨ x2 - 8·x + 12 = 0 ⇔
x = -1 ∨ x2 - 8·x + 12 = 0 ⇔
x = -1 ∨ x = 4 ± 0,5·√[64 - 4·12] ⇔
x = -1 ∨ x = 4 ± 0,5·√16 ⇔
x = -1 ∨ x = 4 ± 0,5·4 ⇔
x = -1 ∨ x = 4 ± 2 ⇔
x = -1 ∨ x = 4 ± 2 ⇔
x = -1 ∨ x = 2 ∨ x = 6
-
For hvilke værdier af k har polynomiet netop 1 rod?
-
For hvilke værdier af k har graferne for de to funktioner netop et skæringspunkt?
Givet andengradspolynomiet p(x) = x2 + k·x + 1.
Givet funktionerne:
f(x) = x2 - k·x og
g(x) = x - k
Svar på opgave 5. Rødder for andengradspolynomium.
-
Man skal undersøge løsningerne til andengradsligningen p(x) = 0, dvs. ligningen x2 + k·x + 1 = 0.
p(x) har netop en rod, når denne andengradsligning har netop en løsning.
Dette igen er tilfældet, når diskriminanten til andengradsligningen er 0, hvorved man får, at k skal opfylde betingelsen:
k2 - 4·1·1 = 0 ⇔ k2 = 4 ⇔ k = ± 2.
Dvs. andengradspolynomiet har netop en rod, når k = -2, eller når k = 2
-
De skærer hinanden for x2 - k·x = x - k ⇔ x2 + (1 + k)·x + k = 0.
Man skal finde det eller de k for hvilke, denne andengradsligning har netop en løsning.
Ligningen har diskriminanten: (1 + k)2 - 4·k = k2 - 2·k + 1. Denne skal lig med 0 for, at der er netop en løsning. Man får: k2 - 2·k + 1 = 0 ⇔ k = 1.
De grafer har derfor netop et skæringspunkt, når k = 1
-
Find monotoniforholdene for f.
-
Find monotoniforholdene for g .
Givet funktionen: f(x) = -(4/3)·x3 + x2 + 2x - 5, x∈R.
Givet funktionen: g(x) = (x + 5)·ex, x∈R
Svar på opgave 6. Monotoniforhold.
-
Man skal lave en fortegnsundersøgelse for den afledede funktion.
Den afledede funktion for f er: f '(x) = -4·x2 + 2·x + 2.
Man finder dennes nulpunkter:
f '(x) = 0 ⇔ -4·x2 + 2·x + 2 = 0 ⇔ x = −0,5 ∨ x = 1
Man undersøger fortegn for f ' omkring nulpunkterne:
f '(-1) = -4·(-1)2 + 2·(-1) + 2 = -4 (dvs. f ' er negativ for x mindre end -0,5)
f '(0) = -4·0 + 2·0 + 2 = 2 (dvs. f ' er positiv for x mellem -0,5 og 1)
f '(2) = -4·22 + 2·2 + 2 = -10 (dvs. f ' er negativ for x større end 1).
Dvs: f er aftagende for x < -0,5, voksende for -0,5 < x < 1 og aftagende for x > 1
-
Den afledede funktion for g er: g'(x) = (x + 6)·ex. Det bemærkes, at ex > 0 for alle x.
Man finder dennes nulpunkter:
g'(x) = 0 ⇔ x2 + 6 = 0 ∨ ex = 0 ⇔
g'(x) = 0 ⇔ x2 + 6 = 0 ∨ (falsk for alle x) ⇔
g'(x) = 0 ⇔ x + 6 = 0 ⇔ x = −6
Man laver en fortegnsundersøgelse for g' omkring nulpunkterne:
g'(-7) = (-7 + 6)·e-7 = -e-7 (dvs. g' er negativ for x mindre end -6, da e-7 > 0)
g'(-5) = (-5 + 6)·e-5 = e-5 (dvs. g' er positiv for x større end -6, da e-5 > 0)
Dvs. monotoniforholdene er: g er aftagende for x < -6 og voksende for x > -6
Opstil en matematisk model for følgende tilfælde:
-
I et land var der 50.000 biler i 2001. Siden er antallet vokset med 700 biler om året.
-
I en by var der 4.300 huse i 1999. Siden er antallet aftaget med 2 % om året.
-
På en skole var der 300 elever i 2004. Siden er antallet vokset med 1,5 % om året.
-
På en ø var der 2.200 kaniner i 2002. Siden er antallet aftaget med 60 kaniner om året.
Svar på opgave 7. Modeller for vækst.
-
Modellen er lineær og voksende. Grunden er, at antallet øges med et fast antal eller mængde om året.
Man sætter f(x) lig med antallet af biler og x lig med antal år efter 2001. Modellen bliver:
f(x) = 700·x + 50.000
-
Modellen er eksponentiel og aftagende. Grunden er, at antallet falder med en fast procentdel eller ændres med en fast negativ vækstrate om året.
Man sætter f(x) lig med antallet af huse og x lig med antal år efter 1999. Modellen bliver:
f(x) = 4.300·(1 – 2%)x = 4.300·(1 - 0,02)x = 4.300·0,98x
-
Modellen er eksponentiel og voksende. Grunden er, at antallet vokser med en fast procentdel eller ændres med en fast positiv vækstrate om året.
Man sætter f(x) lig med antallet af elever og x lig med antal år efter 2004. Modellen bliver:
f(x) = 300·(1 + 1,5%)x = 300·(1 + 0,015)x = 300·1,015x
-
Modellen er lineær og aftagende. Grunden er, at antallet falder med et fast antal eller mængde om året.
Man sætter f(x) lig med antallet af kaniner og x lig med antal år efter 2002. Modellen bliver:
f(x) = –60·x + 2.200
-
Hvilken kurve passer til hvilken funktion? (Begrund svar).
-
Hvad er skæringspunktet for deres grafer?
Nedenfor er vist graferne for tre førstegradspolynomier.
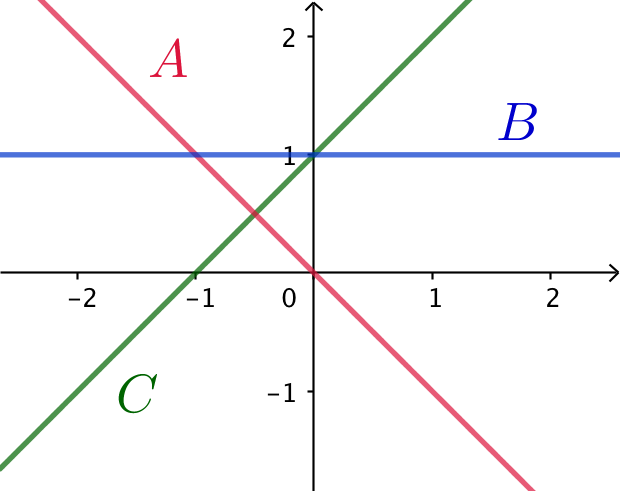
De har forskrifterne
f(x) = x + 1
g(x) = -x
h(x) = 1
To førstegradspolynomier har forskrifterne.
p(x) = 2x + 1
q(x) = -x + 4
Svar på opgave 8. Linjer og ligningssystem.
-
A er en ret linje med negativ hældning, der går igennem (0,0). Dette passer med g, der har koefficienten -1 for x og konstanten 0. Den negative koefficient svarer til et aftagende polynomium og konstanten 0 viser at grafen for polynomiet skærer y-aksen i y = 0.
B er en vandret ret linje, der går igennem (0,1). Dette passer med h, der har koefficienten 0 for x og konstanten 1. Koefficient 0 en vandret linje med hældningen 0. Konstanten 1 viser, at den skærer y-aksen i y = 1.
C er en ret linje, der går igennem (0,1) og har positiv hældning. Dette passer med f, der har koefficienten 1 for x og konstanten 1. Koefficient 1 giver et førstegradspolynomium med positiv hældning og konstanten 1 viser at dens graf skærer y-aksen i y = 1.
-
Man skal løse det sammenhørende lineære ligningssystem:
y = 2x + 1 ∧ y = −x + 4 ⇔
y = 2x + 1 ∧ 2x + 1 = −x + 4 ⇔
y = 2x + 1 ∧ 3x = 3 ⇔
y = 2·1 + 1 ∧ x = 1 ⇔
y = 3 ∧ x = 1
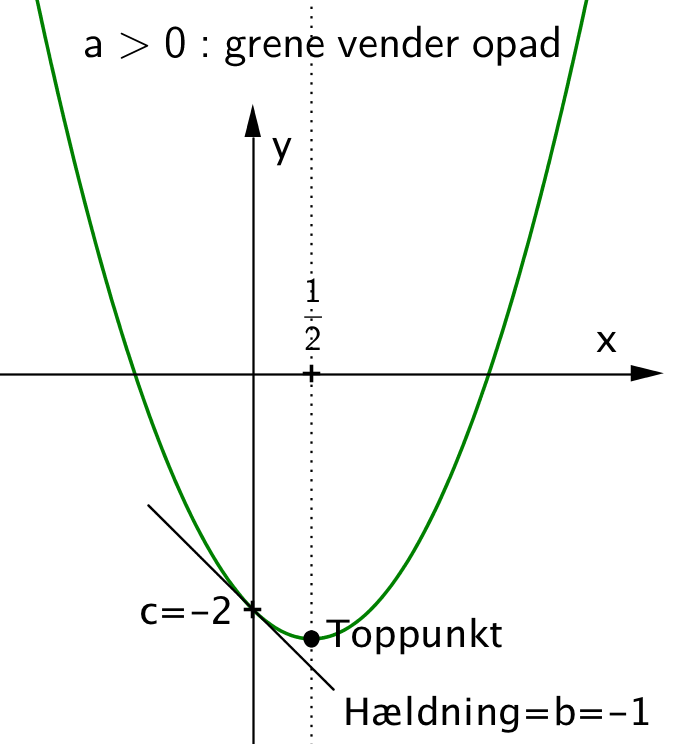
Givet andengradspolynomiet p(x) = -x2 + 4·x - 1.Dvs. skæringspunktet for polynomierne er (x,y) = (1,3)
-
Hvad er toppunktet for den tilhørende parabel?
-
Hvad er b og c?
-
Bestem om a og d er negative, nul eller positive i hvert af de tre tilfælde.
Givet andengradspolynomiet q(x) = x2 + b·x + c, der har rødderne x1 = -7 og x2 = 5.
Nedenfor er graferne for tre andengradspolynomier. Disse har koefficienter a, b og c samt diskriminanten d.
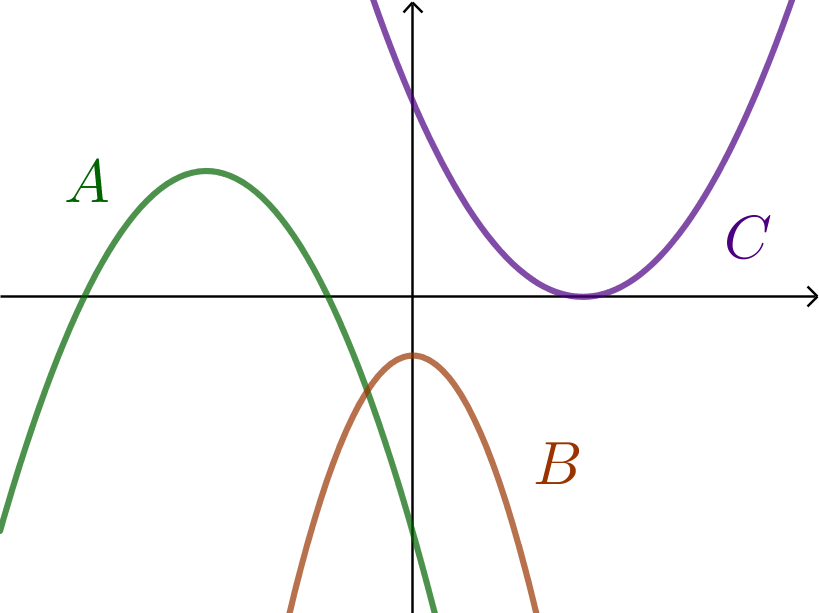
Svar på opgave 9. Parabel og andengradspolynomium.
-
Man skal finde (xT,yT), hvor xT er toppunktets x-koordinat og yT dets y-koordinat.
xT = -b/(2a). Her er a = -1 og b = 4. Man får -4/(2·(-1)) = 2.
yT = f(xT) = p(2) = -22 + 4·2 - 1 = -4 + 8 - 1 = 3.
Dvs. toppunktet er (2,3)
-
q(x) kan skrives a·x2 + b·x + c = a·(x - x1)·(x - x2) = (x + 7)·(x - 5) = x2 + 2·x + (-35).
Heraf ses, at b = 2 og c = -35
-
Hvis a er positiv vender parablens grene opad, og hvis a er negativ vender de nedad. (Det bemærkes, at a ikke kan være 0, da der i så tilfælde ikke er tale om et andengradspolynomium). Dette viser, at a er negativ for A og B, mens a er positiv for C
Hvis d er negativ, så har parablen ingen punkter tilfælles med x-aksen. Hvis d er nul har den eet punkt tilfælles, og hvis d er positiv har den to. Dette viser, at d er positiv for A, mens d er negativ for B, og d er nul for C
-
Hvilken graf passer til hvilken funktion? (Begrund svar)
-
Hvilken graf hører til hvilken funktion? (Begrund svar)
-
Hvilken graf hører til hvilken funktion? (Begrund svar)
Nedenfor er vist tre grafer, A, B og C.
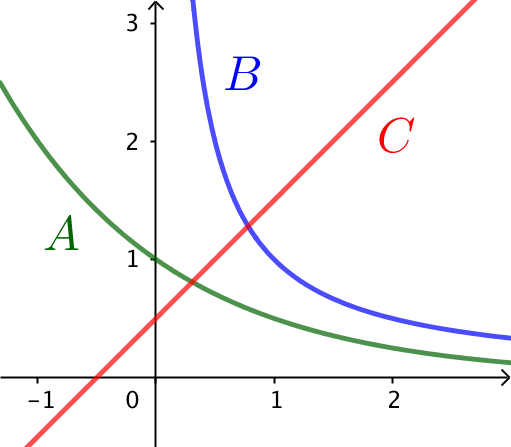
Funktionerne f, g og h, der har forskrifterne:
f(x) = x + 0,5
g(x) = 1/x
h(x) = 2-x
Nedenstående figur viser graferne A og B.
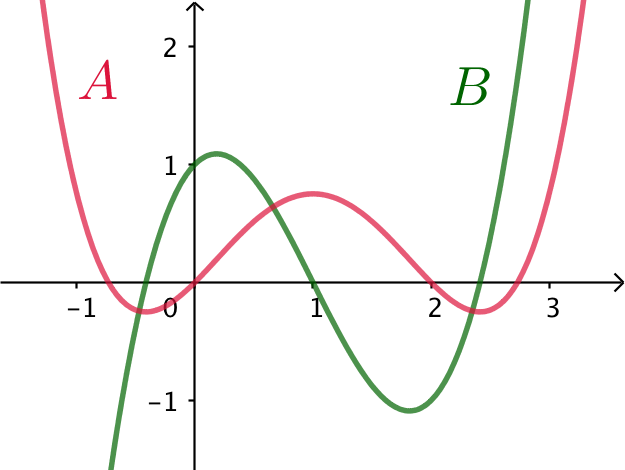
De hører til funktionerne f og g for hvilke der gælder, at f er en stamfunktion til g.
Nedenstående figur viser graferne A, B og C.
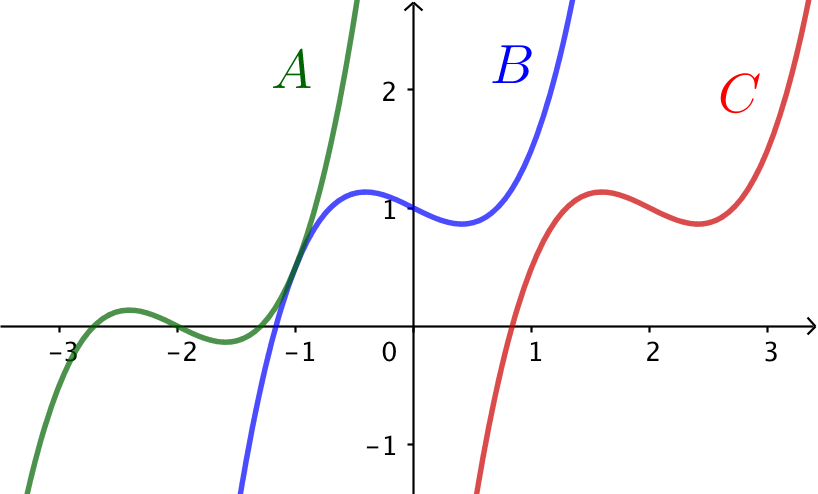
Den ene hører til funktionen f. For de to andre gælder:
g(x) = f(x - 2)
h(x) = f(x + 2) - 1.
Svar på opgave 10. Grafer: lineær/potens/eksponentiel, funktion/stamfunktion og parallelforskydning.
-
Det ses, at C er en ret linje og dermed grafen for en lineær funktion. Dvs. f svarer til C
Man omskriver forskrifterne for g og h:
g(x) = 1/x = x-1 og
h(x) = 2-x = (2-1)x = (1/2)x.
Dette viser at g er en potensfunktion med negativ eksponent, hvilket gør, at dens graf ligger i første kvadrant og er aftagende. Samtidig har man, at h er en eksponentiel funktion med en base, der er mellem 0 og 1, hvilket gør at den er defineret for alle x og aftagende.
Dette viser at g svarer til B og h svarer til A
-
Hvis f er stamfunktion til g, så er g den afledede af f. For en afledet funktion gælder, at den har nulpunkter, der hvor funktionen har ekstrema eller vandret vendetangent.
På figuren nedenunder viser de blå prikker nulpunkter for kurven B, og de vandrette streger markerer ekstrema for kurven A. Det ses, at disse passer sammen.
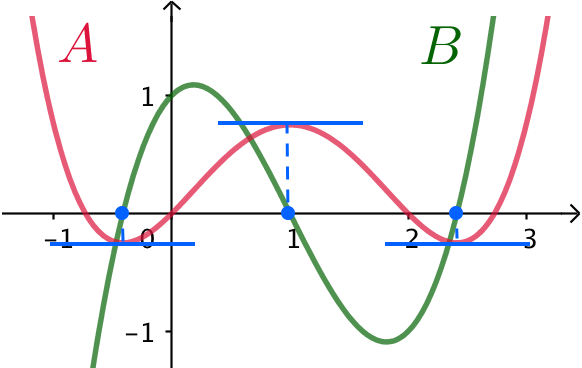
Da nulpunkt for B passer sammen med ekstremum for A, så er B er kurven for funktionen og A er kurven for stamfunktionen
-
Funktionen g med forskriften g(x) = f(x - 2) er parallelforskudt med 2 mod højre i koordinatsystemet i forhold til f. Dette betyder, at f svarer til grafen B, mens g svarer til grafen C.
Dermed svarer graf A til h ifølge udelukkelsesprincippet. Dette passer også med at h(x) = f(x + 2) - 1 svarer til en forskydning af f med 2 mod venstre og 1 ned.
Samlet fås: f svarer til B, g svarer til C og h svarer til A
-
Hvad er |EF|?
-
Hvad er |AE|?
Nedenfor er to retvinklede trekanter, ΔABC og ΔDEF, der har ens vinkler. |AB| = 5, |AC| = 4 og |DF| = 6.
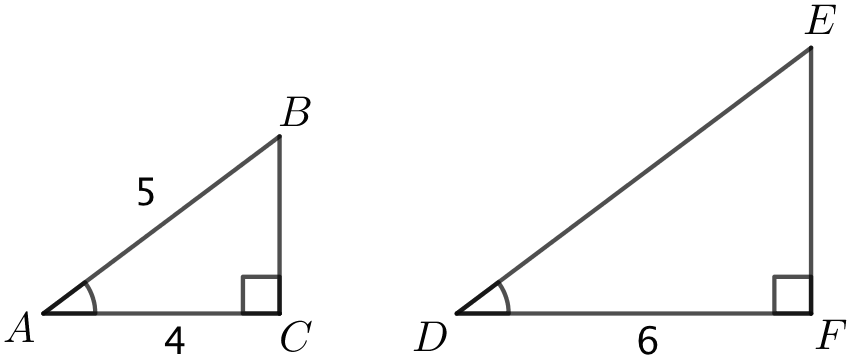
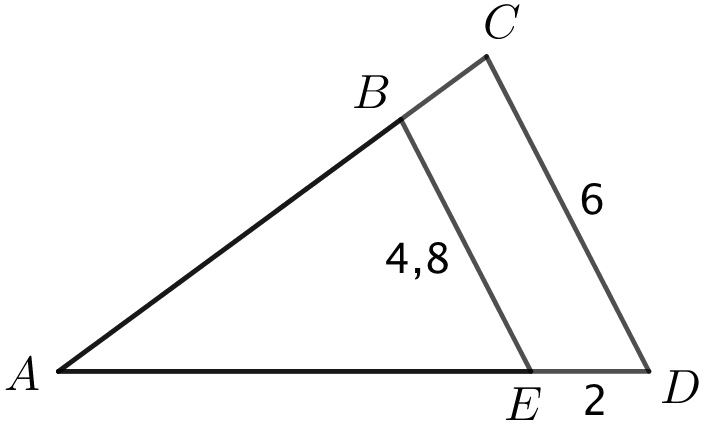
Nedenfor er to ensvinklede trekanter, ΔABE og ΔACD. |BE| = 4,8, |CD| = 6 og |DE| = 2.
Svar på opgave 11. Plangeometri: Ligedannede trekanter.
-
Da trekanterne ΔABC og ΔDEF er ensvinklede, så er ensliggende sider proportionale. Dermed gælder, at |EF|/|BC| = |DF|/|AC| ⇒
|EF| = |BC|·|DF|/|AC| ⇒
|EF| = |BC|·6/4 ⇒
|EF| = 1,5·|BC|.
|BC| kan findes ved hjælp af Pythagoras læresætning: |AB|2 = |BC|2 + |AC|2 ⇔
|BC|2 = |AB|2 - |AC|2 ⇒
|BC|2 = 52 - 42 ⇔
|BC|2 = 25 - 16 ⇔
|BC|2 = 9 ⇒
|BC| = 3
Dvs. |EF| = 1,5·3 = 4,5
-
Da trekanterne ΔABE og ΔACD er ensvinklede, så gælder, at |AE|/|AD| = |BE|/|CD| ⇔
|AE| = |AD|·|BE|/|CD| ⇔
|AE| = (|AE| + |DE|)·|BE|/|CD| ⇔
|AE| = |AE|·|BE|/|CD| + |DE|·|BE|/|CD| ⇔
|AE| - |AE|·|BE|/|CD| = |DE|·|BE|/|CD| ⇔
|AE|·(1 - |BE|/|CD|) = |DE|·|BE|/|CD| ⇔
|AE| = (|DE|·|BE|/|CD|)/(1 - |BE|/|CD|) ⇒
|AE| = (2·4,8/6)/(1 - 4,8/6) ⇔
|AE| = 1,6/0,2 ⇔
|AE| = 8
Dvs. |AE| = 8
-
Find centrum og radius for cirklen og vis, at punktet (-2,-1) ligger på ciklens periferi.
-
Find centrum og radius for cirklen.
Givet en cirkel med ligningen: (x + 4)2 + (y - 1)2 = 8
Givet en cirkel med ligningen: x2 + 4·x + y2 - 12·y + 24 = 0
Svar på opgave 12. Plangeometri: cirkler.
-
En cirkel med en ligning på standardform: (x - a)2 + (y - b)2 = r2 har centrum i (a,b) og radius r.
Ligningen: (x + 4)2 + (y - 1)2 = 8
kan omskrives til: (x - (-4))2 + (y - 1)2 = (√8)2
Dvs. cirklen har centrum i (-4,1) og radius = √8
For at vise at punktet (x,y) = (-2,-1) ligger på cirkelperiferien, så indsætter man x = -2 og y = -1 i cirklens ligning og gør prøve:
Venstre side: (-2 + 4)2 + (-1 - 1)2 = 22 + (-2)2 = 4 + 4 = 8
Højre side: 8
Da venstre og højre side giver det samme, så stemmer prøven og punktet (-2,-1) ligger på cirklen.
-
Man bruger kvadratkomplettering for at omskrive cirklens ligning til formen: (x - a)2 + (y - b)2 = r2.
x2 + 4·x + y2 - 12·y + 24 = 0 ⇔
x2 + 4·x + y2 + (-12)·y + 24 = 0 ⇔
x2 + 4·x + (4/2)2 - (4/2)2 + y2 + (-12)·y + ((-12)/2)2 - ((-12)/2)2 + 24 = 0 ⇔
x2 + 4·x + 22 - 22 + y2 - 12·y + (-6)2 - (-6)2 + 24 = 0 ⇔
(x2 + 4·x + 22) + (y2 - 12·y + (-6)2) + (-22 - (-6)2 + 24) = 0 ⇔
(x - (-2))2 + (y - 6)2 + (-4 + 36 - 24) = 0 ⇔
(x - (-2))2 + (y - 6)2 - 16 = 0 ⇔
(x - (-2))2 + (y - 6)2 = 42
Dvs. cirklen har centrum i (-2,6) og radius = 4
-
For hvilke værdier af t er a og b ortogonale?
-
For hvilke værdier af s er vektorerne u og v parallelle?
-
Hvad er arealet af det parallelogram, som vektorerne u og v udspænder, når s = 5.
Givet vektorerne a = (1,t) og b = (3,-1), hvor t∈R.
Givet vektorerne u = (s,2) og v = (-3,4), hvor s∈R.
Svar på opgave 13. Vektorer i planen.
-
a og b er egentlige. Hvis deres skalarprodukt er lig med nul er de ortogonale. Man skal finde det t, der opfylder dette:
a·b = 0 ⇒
(1,t)·(3,-1) = 0 ⇔
1·3 + t·(-1) = 0 ⇔
3 - t = 0 ⇔
t = 3
Dvs. a og b er ortogonale for t = 3
-
u og v er egentlige. De er parallelle, hvis skalarproduktet af u og tværvektoren til v er lig med nul.
v = (-3,4) og har dermed tværvektoren (-4,-3). Man skal dermed finde det s, der opfylder følgende ligning:
(s,2)·(-4,-3) = 0 ⇔
s·(-4) + 2·(-3) = 0 ⇔
-4·s - 6 = 0 ⇔
s = -3/2
Dvs. u og v er parallelle for s = -3/2
-
Når s = 5, så er u = (5,2). Arealet af det parallelogram som u og v udspænder er lig med den numeriske værdi af skalarproduktet af u og tværvektoren til v, der som før er (-4,-3). Man får:
|(5,2)·(-4,-3)| = |5·(-4) + 2·(-3)| = |-20 - 6| = |-26| = 26
Dvs. arealet af det udspændte parallelogram er 26
-
Find alle stamfunktioner til f.
-
Hvilken af disse stamfunktioner går gennem punktet (1,2)
Man har funktionen f(x) = x2 - 2·x + 2.
Svar på opgave 14. Stamfunktioner.
-
En tilfældig valgt stamfunktionen til f(x) kaldes F(x).
Der gælder, at samtlige stamfunktioner er F(x) + K, hvor K ∈R.
Man vælger F(x) = (1/3)·x3 - x2 + 2·x, hvorved samtlige stamfunktioner til f(x) bliver
F(x) + K = (1/3)·x3 - x2 + 2·x + K
(Der er brugt konstant-reglen, sum-reglen og potens-reglen i beregningen af F(x)).
-
Man skal bestemme K, så der gælder, at F(1) + K = 2. Man får:
F(1) + K = 2 ⇒
(1/3)·13 - 12 + 2·1 + K = 2 ⇔
1/3 - 1 + 2 + K = 2 ⇔
K = 2/3
Dvs. den stamfunktion til f(x), der går gennem punktet (1,2) er F(x) + 2/3 = (1/3)·x3 - x2 + 2·x + 2/3
Man har differentialligningen:
dy/dx = 2·y·x.
Nedenstående spørgsmål ønskes besvaret uden, at man løser differentialligningen:
-
Er funktionen: f(x) = ex2 en løsning til differentialligningen?
-
Hvad er ligningen for tangenten til denne graf i P?
Grafen til en af differentialligningens løsninger går gennem punktet P = (3,1).
Svar på opgave 15. Differentialligninger.
-
Man gør prøve for at se, om den formodede løsning stemmer med differentialligningen:
Venstre side: dy/dx = f '(x) = 2·x·ex2
Højre side: 2·y·x = 2·ex2·x = 2·x·ex2
Da prøven stemmer, så er f(x) en løsning til differentialligningen.
-
Lad g(x) være den søgte løsning til differentialligningen.
Tangenten til grafen for g(x) i punktet (a,b) har ligningen:
y = g'(a)·(x - a) + b ⇒ y = g'(3)·(x - 3) + 1, hvor man mangler at finde g'(3).
Fra differentialligningen ved man, at g'(x) = 2·g(x)·x og dermed har man, at g'(3) = 2·g(3)·3 = 2·1·3 = 6.
Dette indsættes i ligningen:
y = 6·(x - 3) + 1 ⇔ y = 6·x - 17
Dvs. tangenten i punktet (3,4) til den løsning, der går igennem dette punkt, er y = 6·x - 17
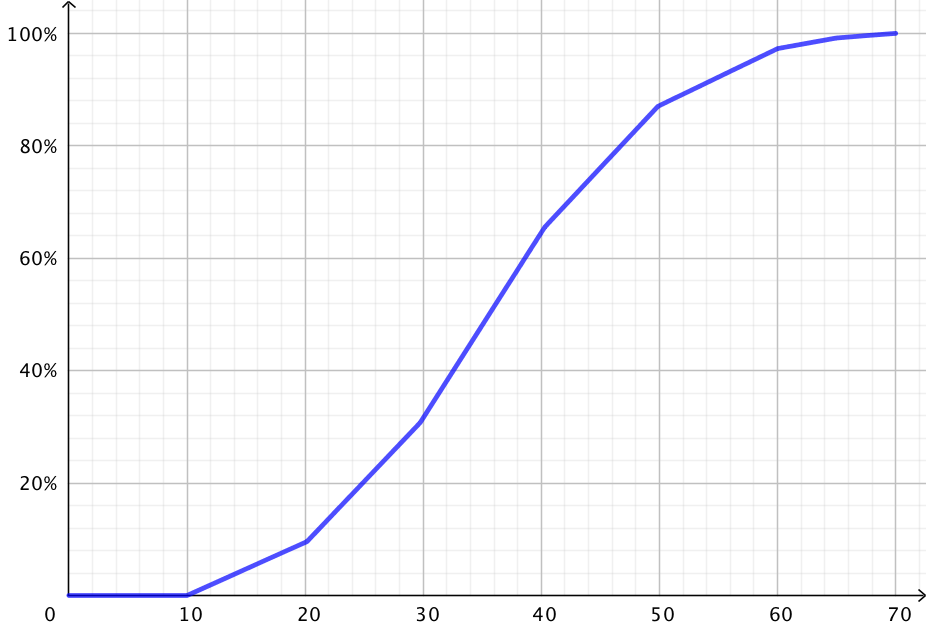
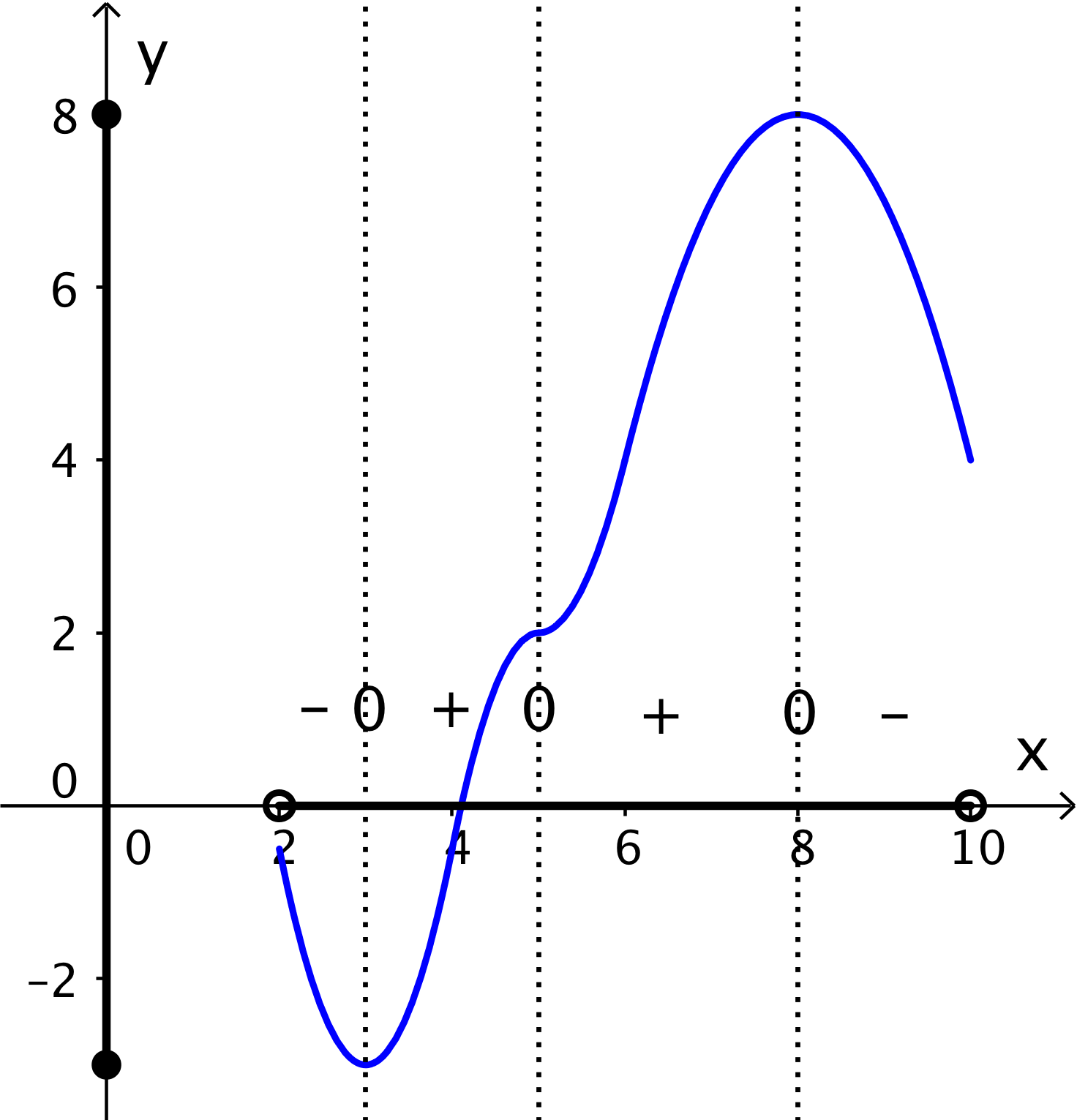
Aldersfordelingen for en gruppe på 90 personer er vist ved hjælp af sumkurven nedenfor
-
Hvor mange personer i gruppen er ældre end 30 år og yngre end eller lig med 40 år?
Svar på opgave 16. Sumkurve.
-
Som vist nedenunder, er ca. 32 % af personerne er mindre end eller lig med 30 år og ca. 65 % er mindre end eller lig med 40 år.
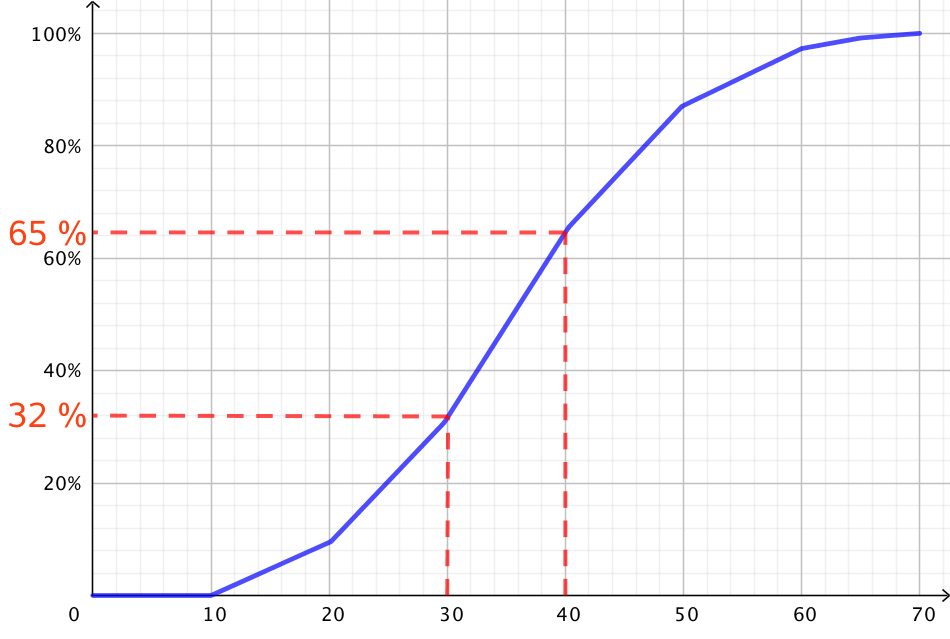
Trækkes det første tal fra det sidste, så får man procentdelen af personer, der er ældre end 30 år og yngre end eller lig med 40 år.
Denne procentdel er 65 % - 32 % = 33 %.
Da der er 90 personer i gruppen, svarer dette til (33 %)·90 personer = 29,7 personer = 30 personer
| Gamle opgaver. Indhold: | |
|
Første- og andengradspolynomier: 7, 9 og 10 |
Integraler: 15, 16, 24, 25, 26, 27, 28 og 29 Eksponentialfunktion: 20 og 21 |
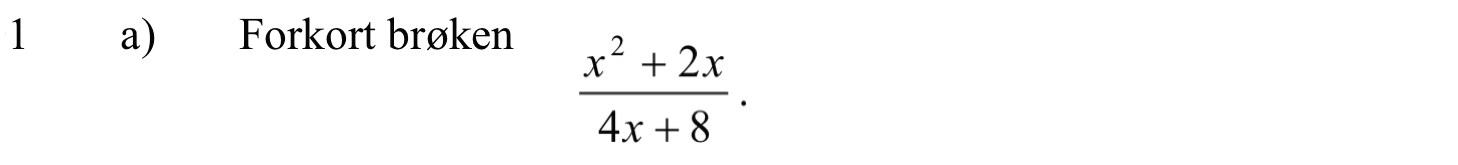
Svar på opgave 1:
Man faktoriserer tæller og nævner og forkorter ens led mellem tæller og nævner.
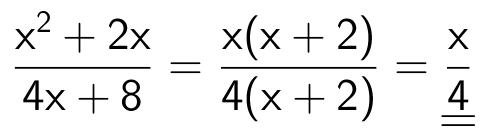
Svar på opgave 2:
Man ganger parenteser ud, samler faktorer og forkorter ens faktorer ud.
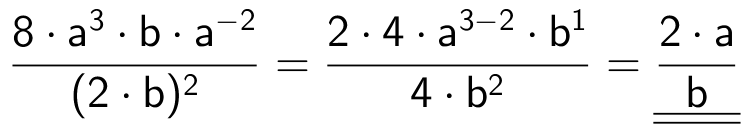
Svar på opgave 3:
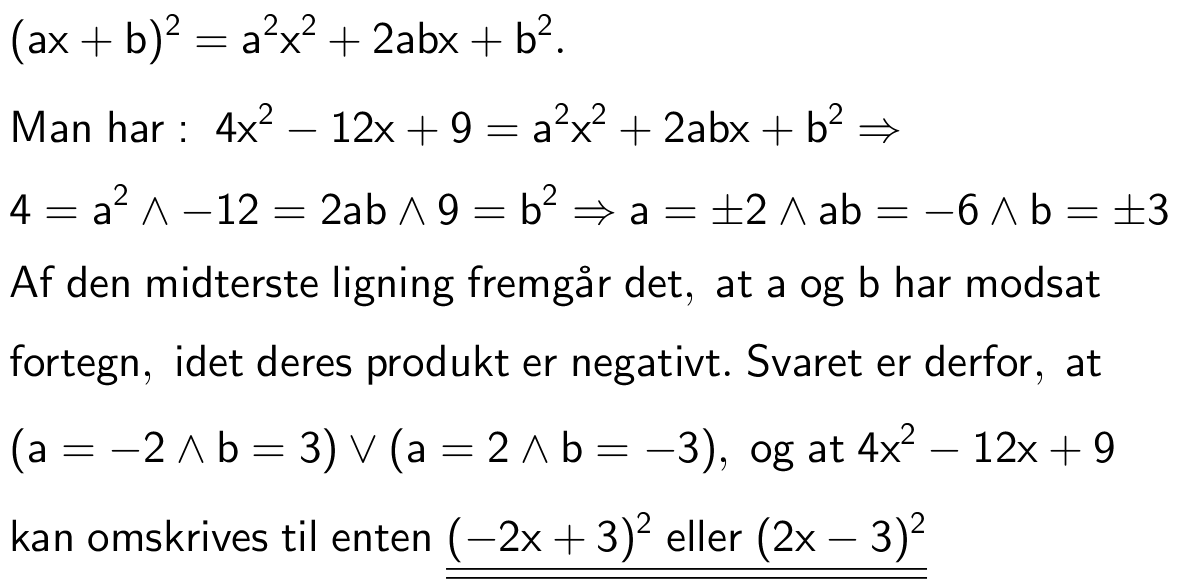
Svar på opgave 4:
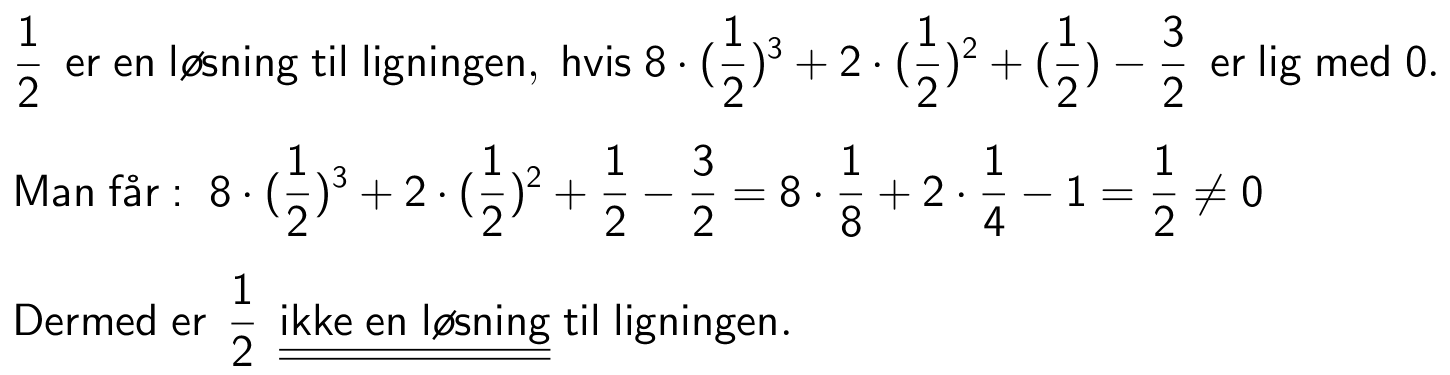
Svar på opgave 5:
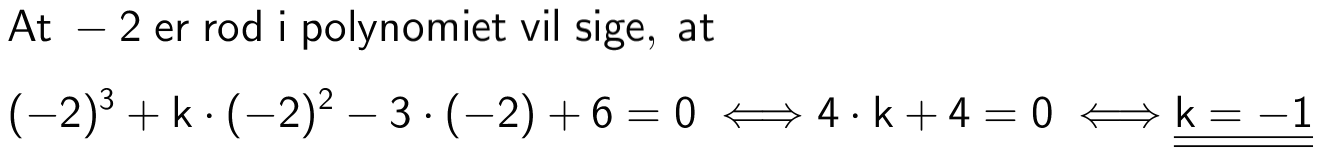
Svar på opgave 6:
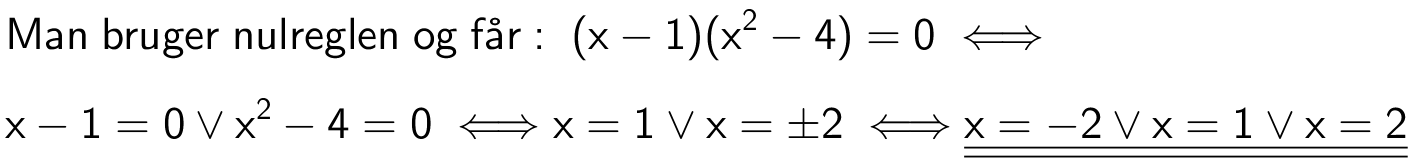
Svar på opgave 7:
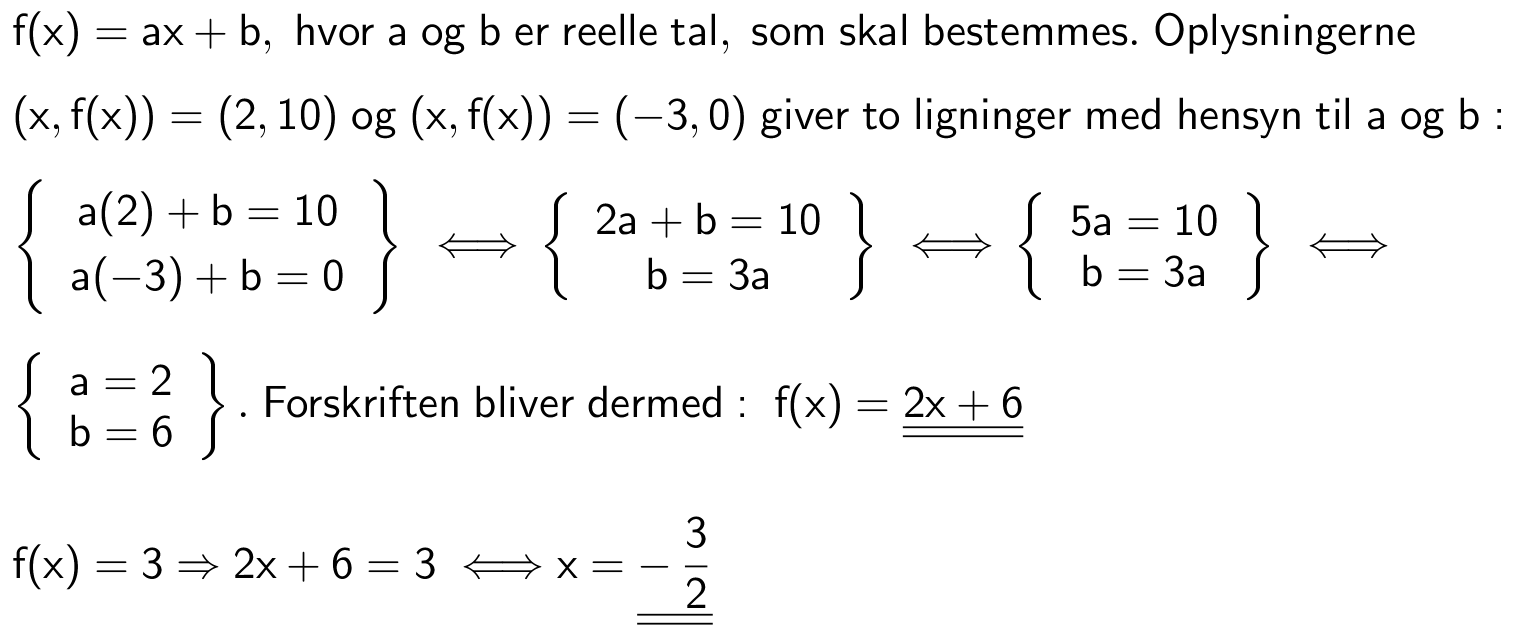
Svar på opgave 8:

Svar på opgave 9:
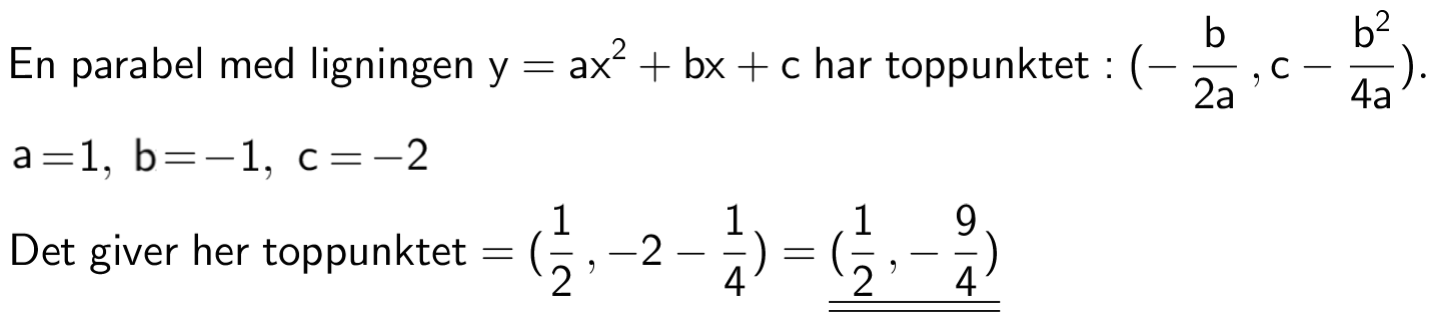
Svar på opgave 10:

Svar på opgave 11:
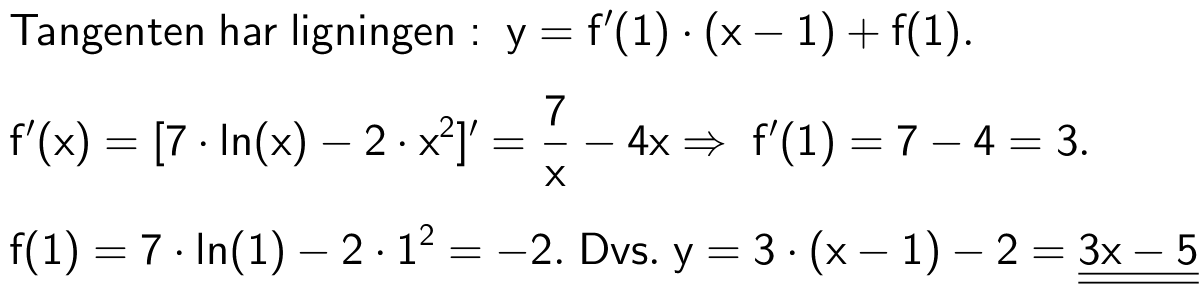
Svar på opgave 12:

Svar på opgave 13:
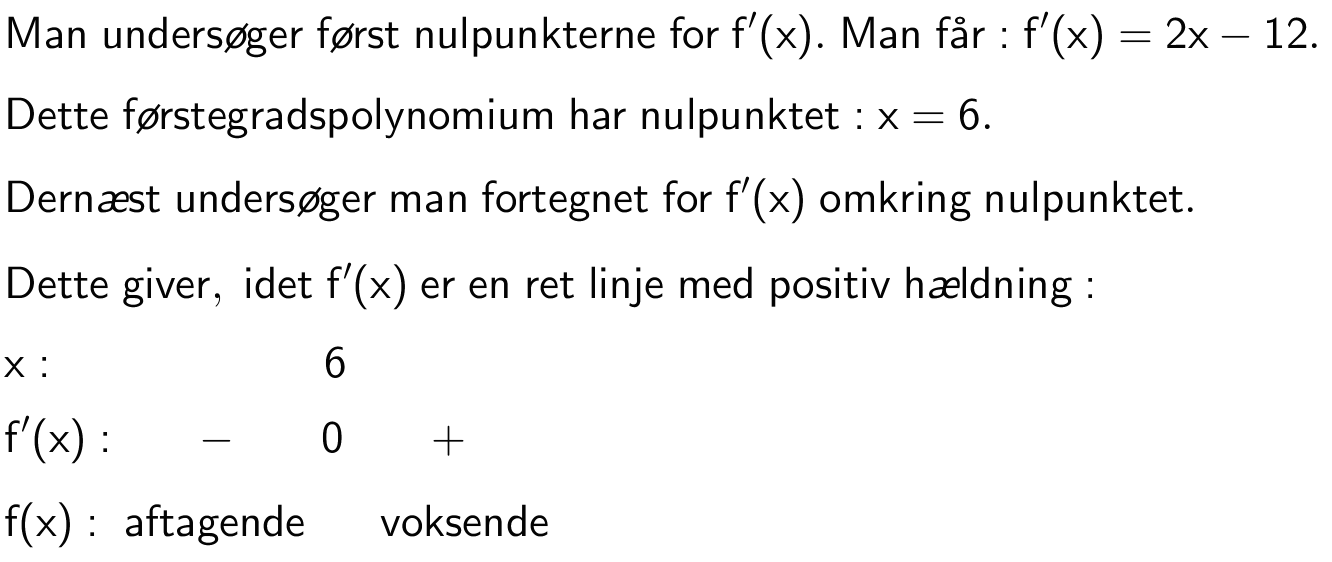
Svar på opgave 14:

Svar på opgave 15:
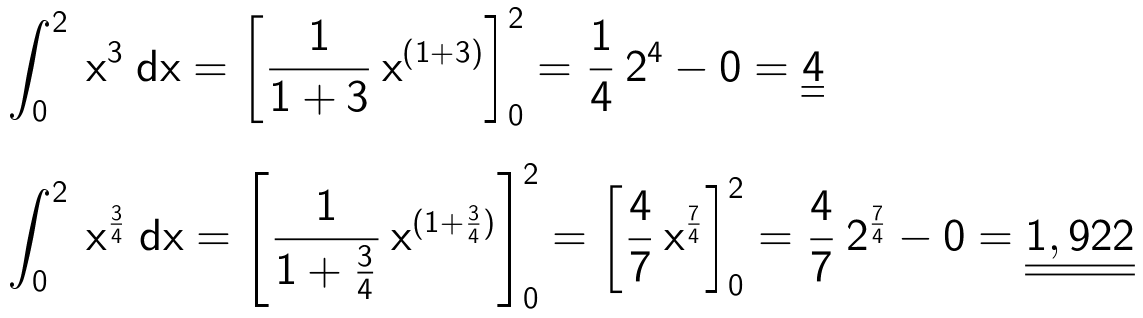
Svar på opgave 16:
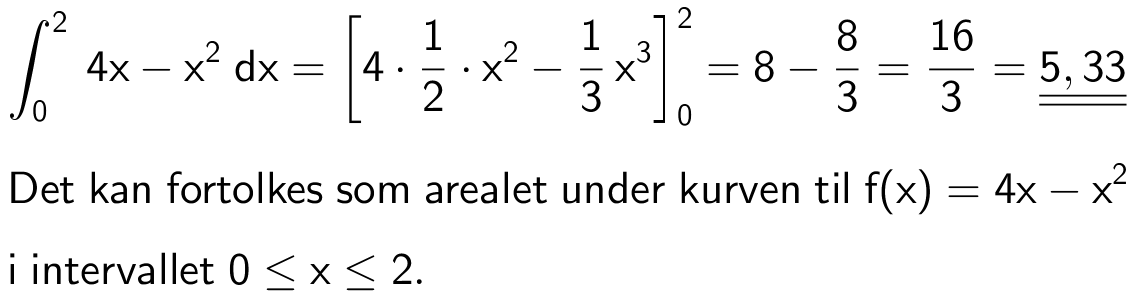
Svar på opgave 17:
Parenteser ganges ud, og led med ens ubekendte eller ens produkter af ubekendte samles. Leddene summeres og ens led med modsat fortegn forsvinder. Den rest, der bliver tilbage, er resultatet.
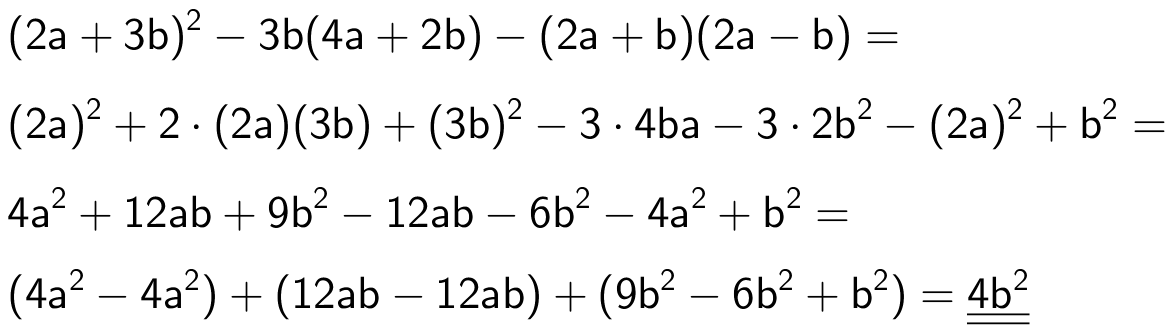
Svar på opgave 18:
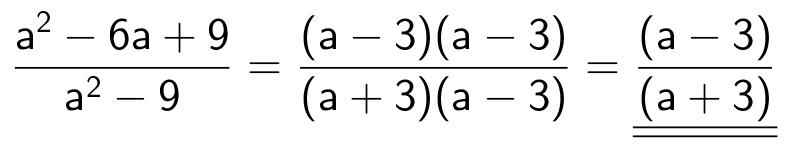
Svar på opgave 19:

Svar på opgave 20:
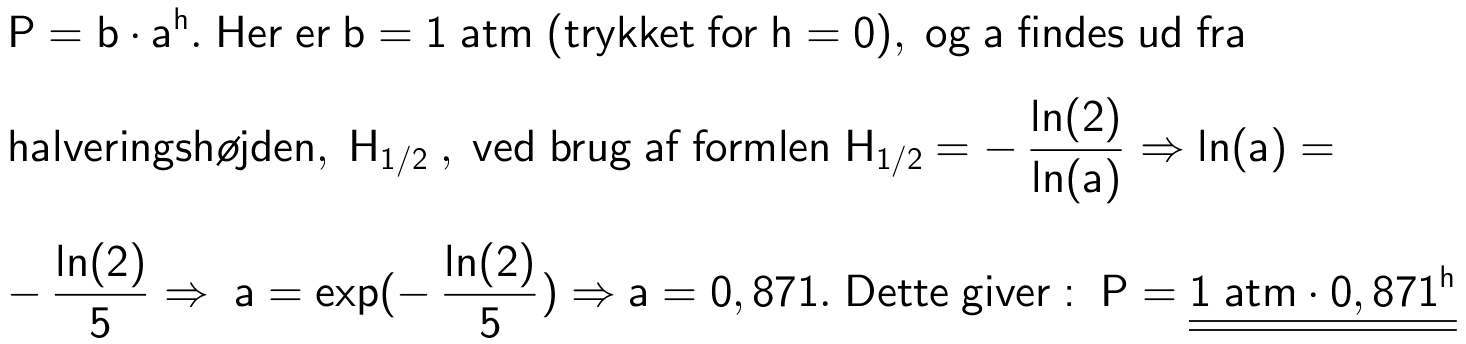
Svar på opgave 21:

Svar på opgave 22:

Svar på opgave 23:

Svar på opgave 24:
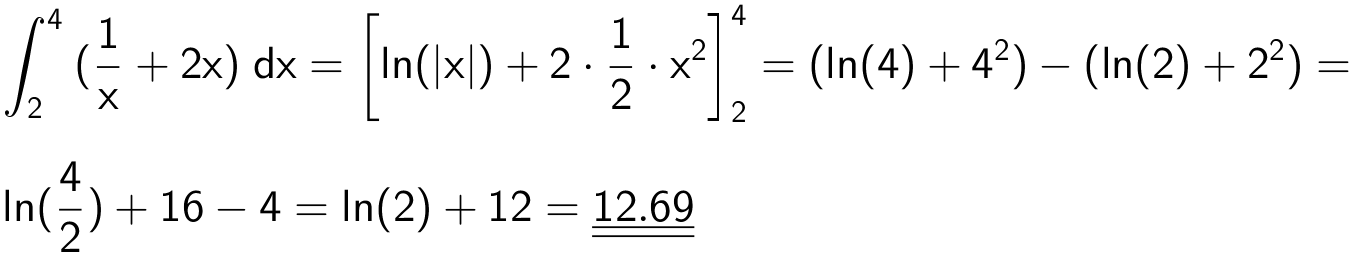
Svar på opgave 25:

Svar på opgave 26:
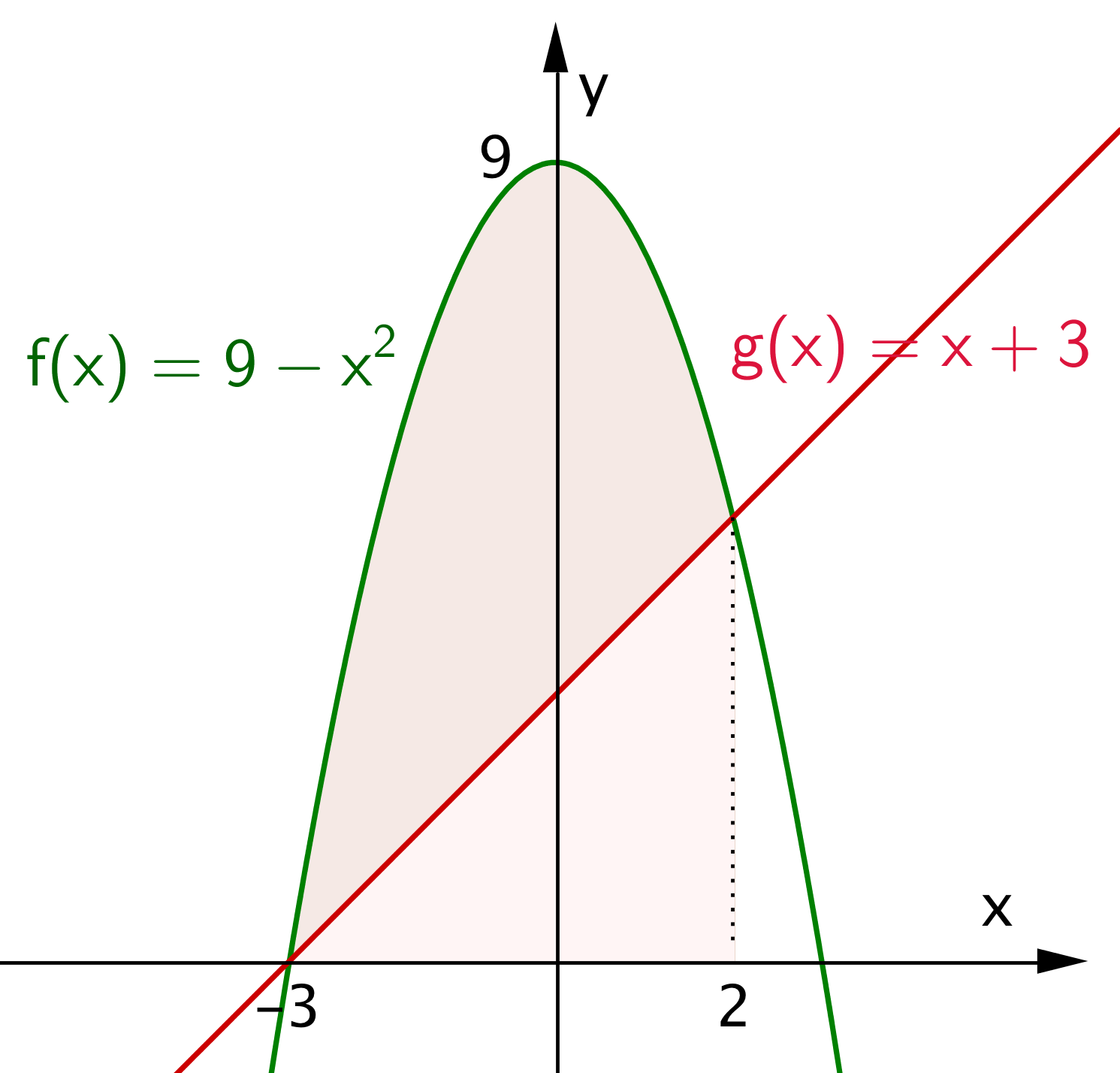
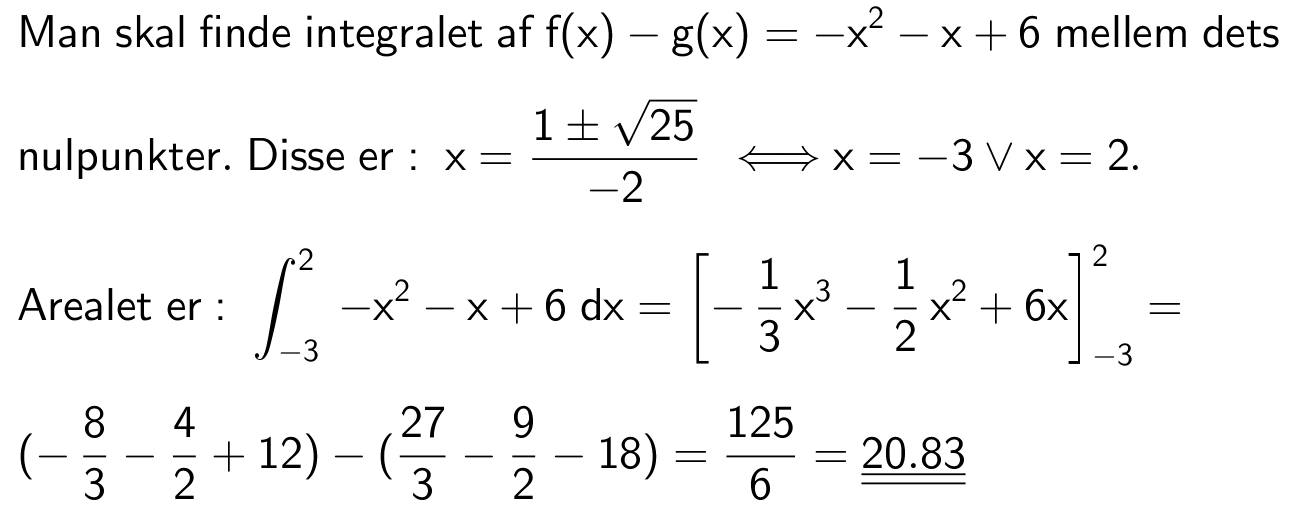
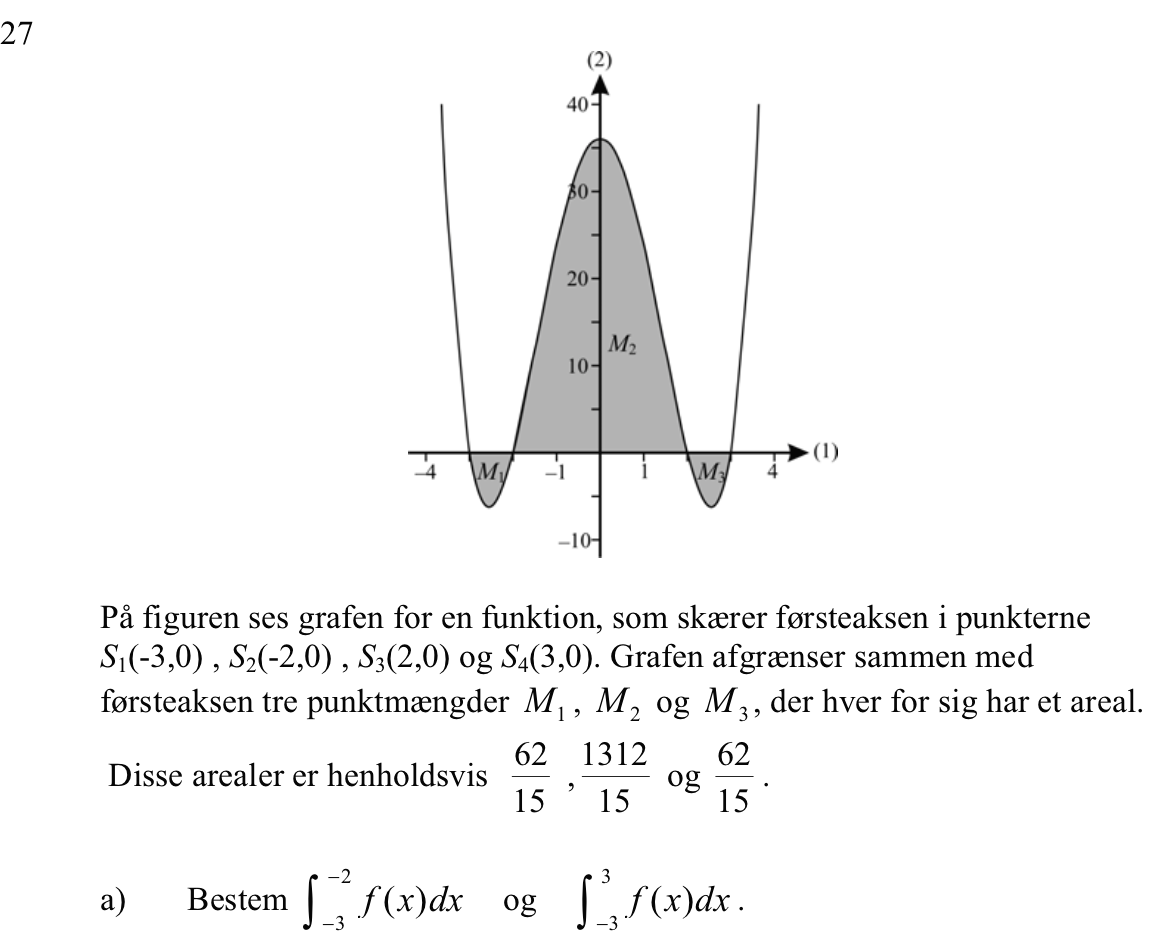
Svar på opgave 27:
Itegralet er summen af arealerne regnet med fortegn mellem de x-værdier, der er grænser for integralet.
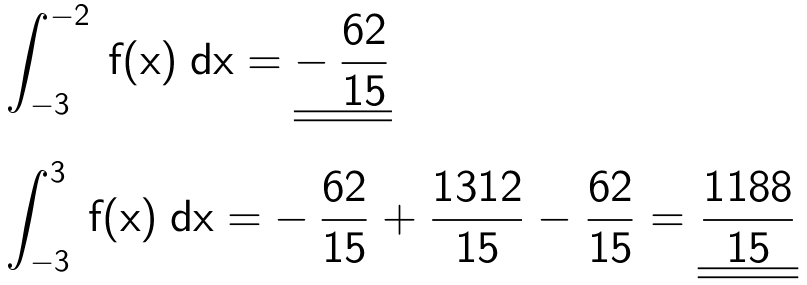
Svar på opgave 28:
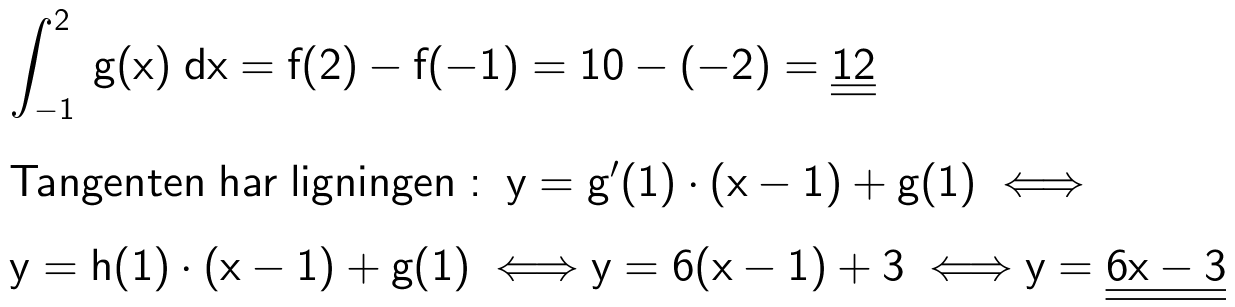
Svar på opgave 29:
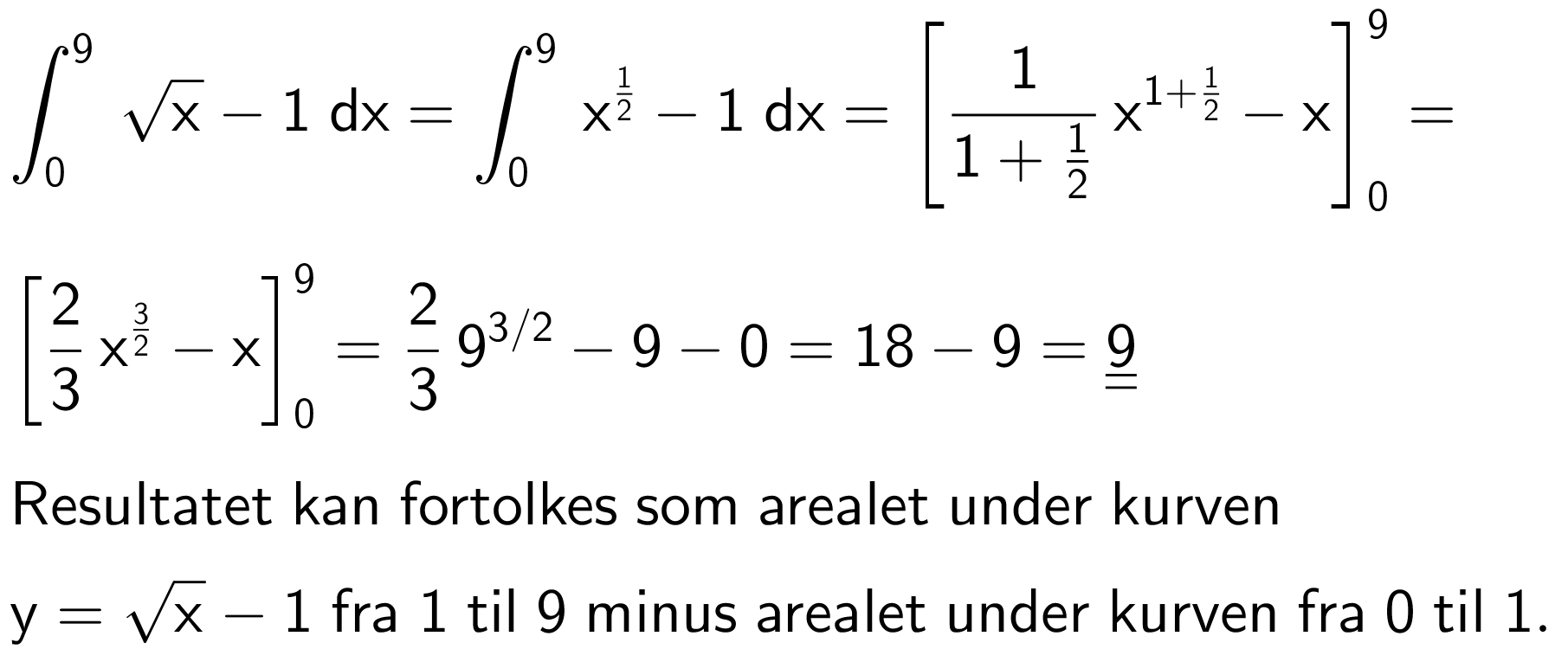
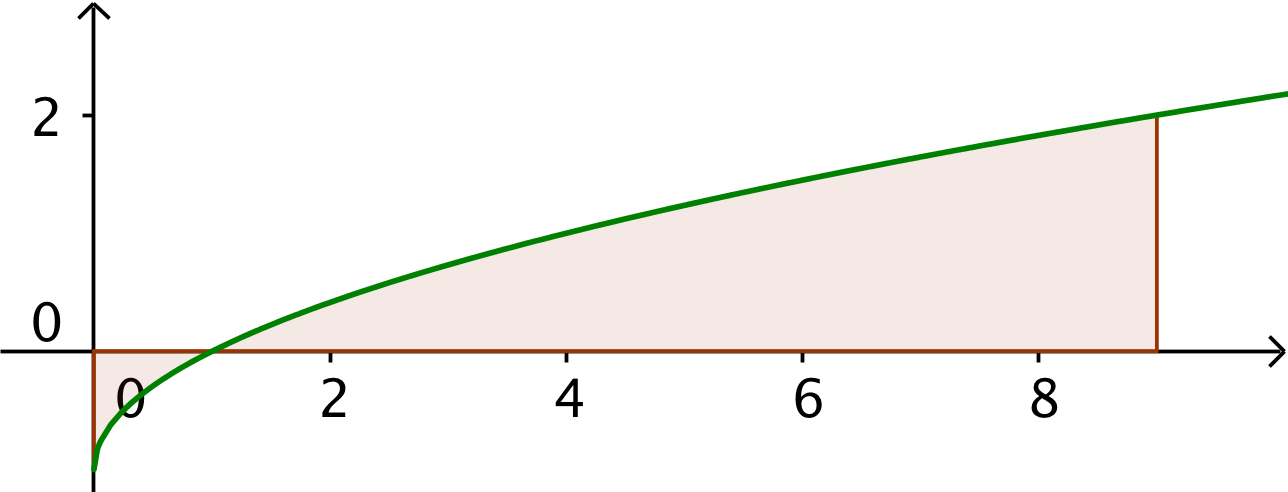
Svar på opgave 30:
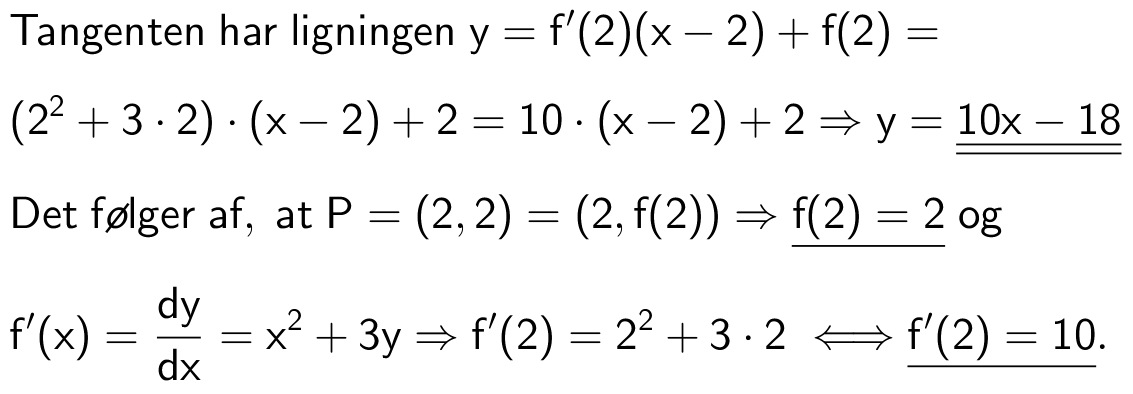
Svar på opgave 31:

Svar på opgave 32:
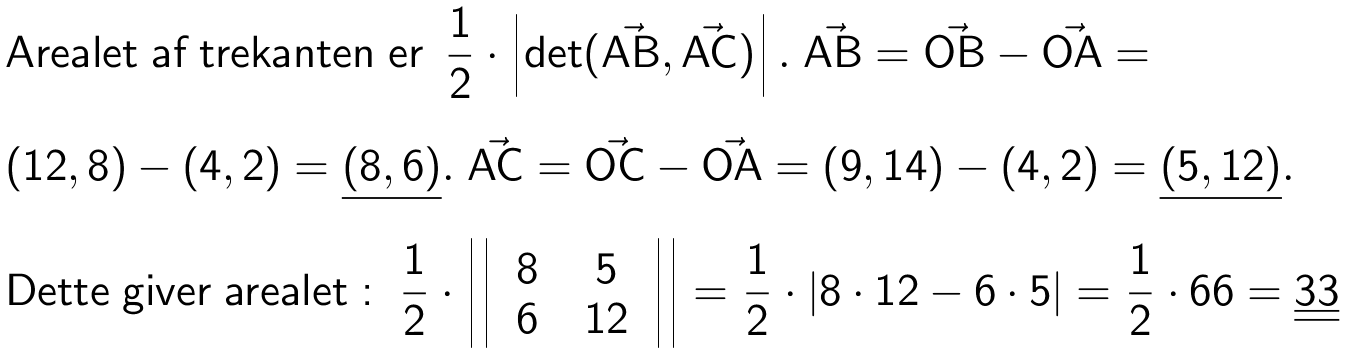
Svar på opgave 33:
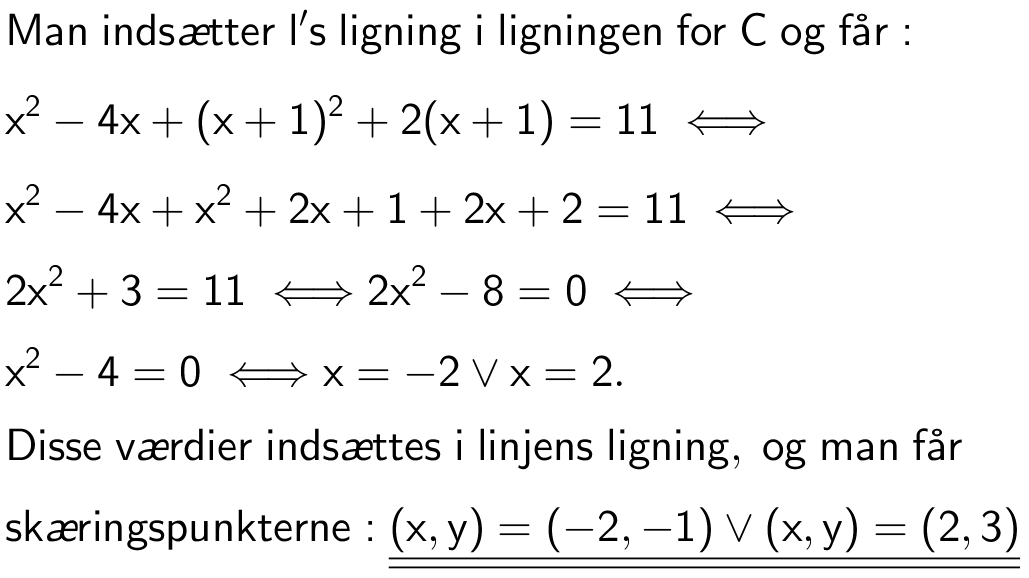
Svar på opgave 34:
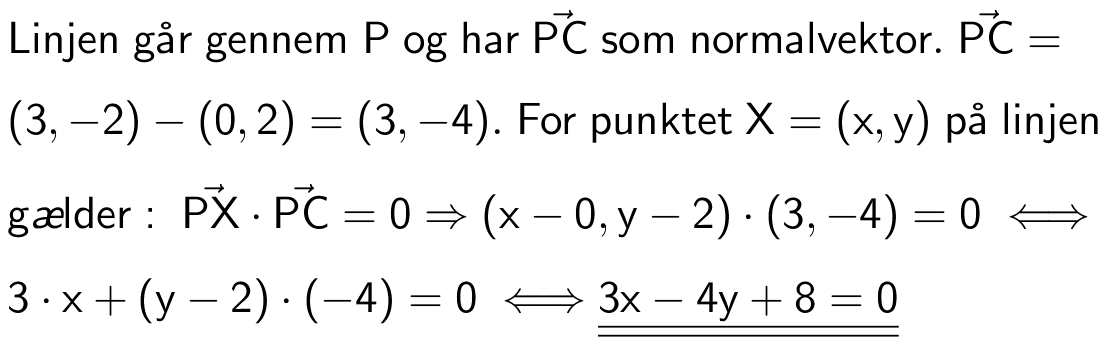
Svar på opgave 35:

Svar på opgave 36:
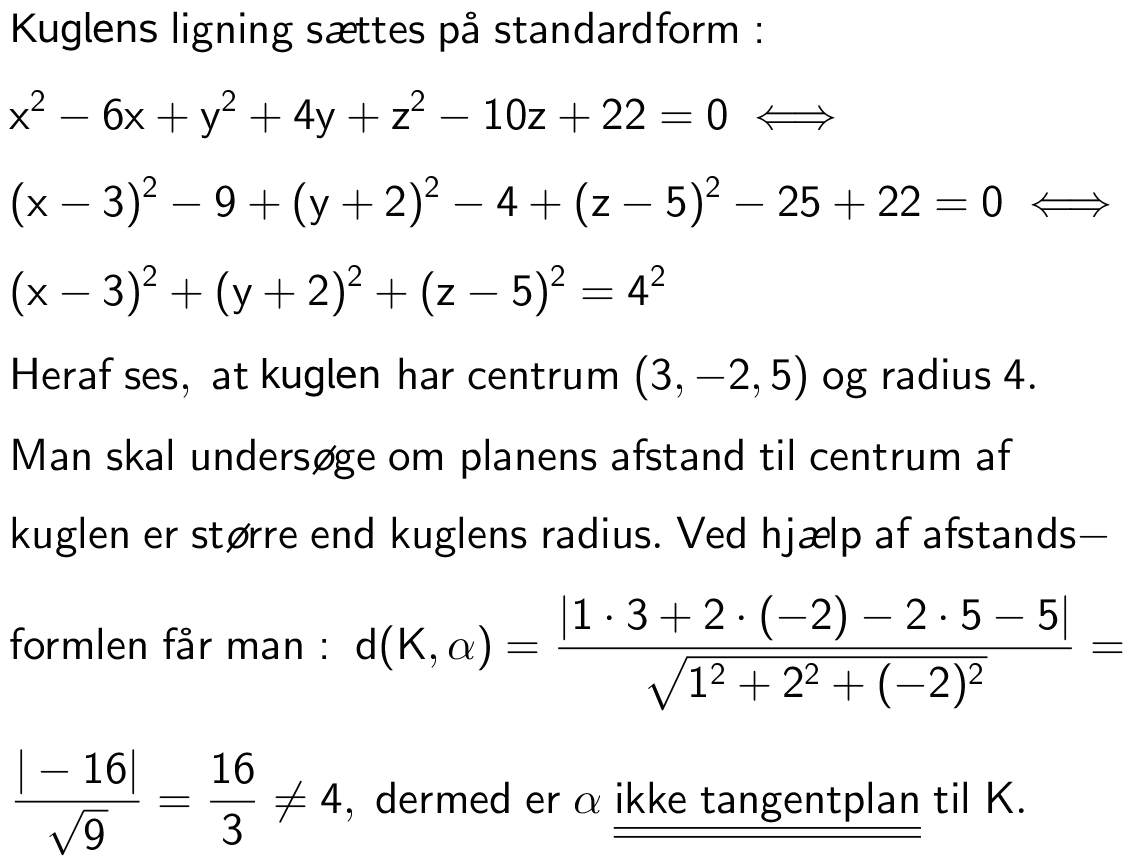
Svar på opgave 37:
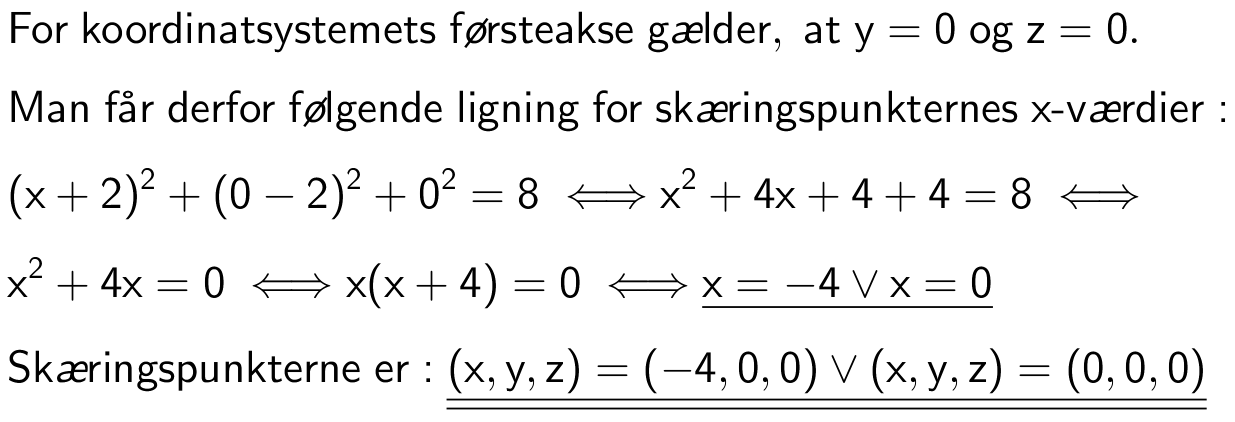
Svar på opgave 38:

Svar på opgave 39:

Svar på opgave 40:
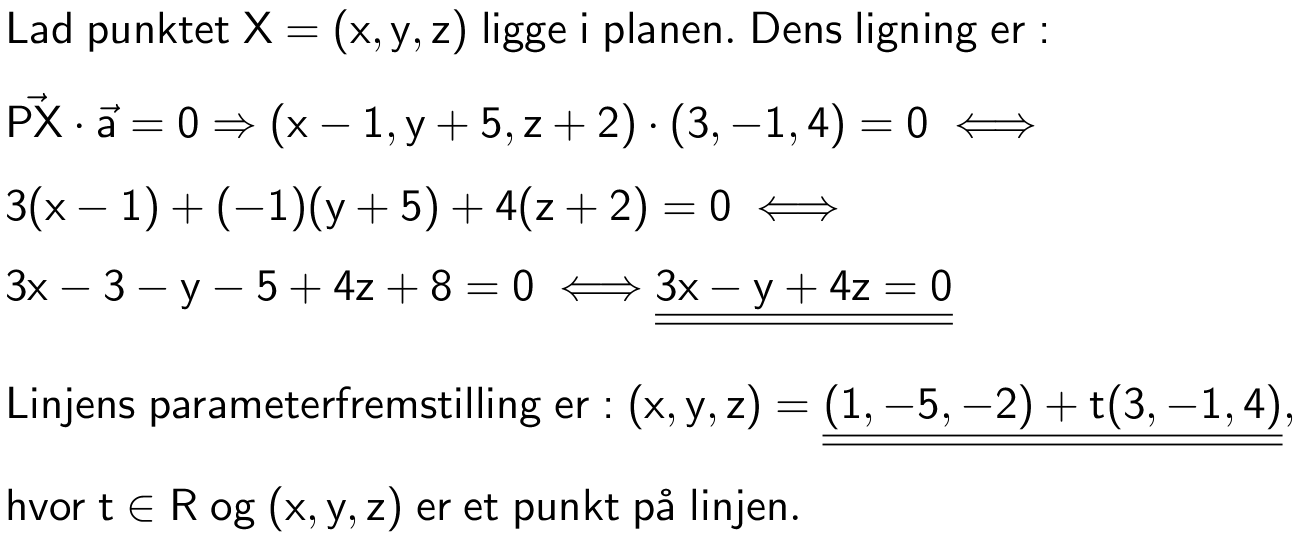
Svar på opgave 41: