Svar på opgave 1:

1. Man har to ligninger med to ubekendte, der skal løses med hensyn til a og b (x og y er her kendte):

   a·1 + b = 2 ∧ a·3 + b = 8 ⇔

   a = 2 - b ∧ (2 - b)·3 + b = 8 ⇔

   a = 2 - b ∧ 6 - b·3 + b = 8 ⇔

   a = 2 - b ∧ -b·2 = 8 - 6 ⇔

   a = 2 - b ∧ b = -2/2 ⇔

   a = 2 - (-1) ∧ b = -1 ⇔

   a = 3 ∧ b = -1

Svar på opgave 2:

1. Løsning:

   x² - 10·x + 21 = 0 ⇔

   x = 10/2 ± (1/2)·√[10² - 4·1·21] ⇔

   x = 5 ± (1/2)·√[100 - 84] ⇔

   x = 5 ± (1/2)·√16 ⇔

   x = 5 ± 2 ⇔

   x = 3 ∨ x = 7

Svar på opgave 3:

1. Siderne AC og AC₁ er ensliggende. Forholdet mellem deres længder er derfor lig med skaleringsfaktoren. Man får:

   |AC₁| = 2·|AC| = 2·5 = 10

   Trekant ABC er retvinklet. Derfor kan man bruge Pythagoras læresætning til at finde |BC|, der er den ene katete:

   |BC| = √[|AB|² - |AC|²] = √[6² - 5²] = √11

Svar på opgave 4:

1. Isolering:

   h/2 - 10 = m ⇔

   h/2 = m + 10 ⇔

   h = 2·m + 20

Svar på opgave 5:

1. Sumkurven viser, hvor stor en procentdel af mændene, der er under eller har en given alder.

   

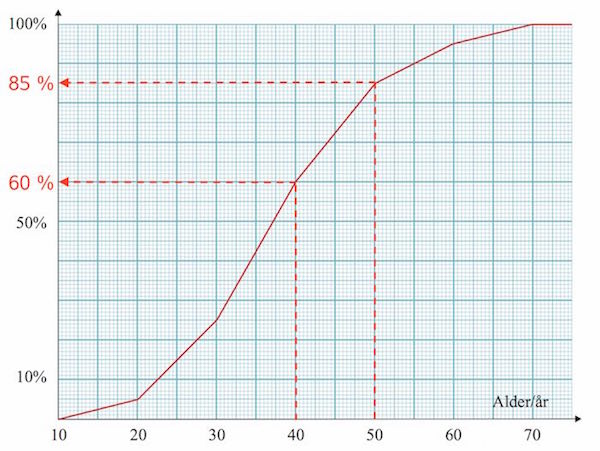
   Det ses, at 85 % er mindre end eller lig med 50 år og 60 % er mindre end eller lig med 40 år.

   Andelen, der er over 40 år og mindre end eller lig med 50 år, er: 85 % - 60 % = 25 %.

   Dermed er der (25 %)·80 mænd = 20 mænd i det pågældende aldersinterval.

Svar på opgave 6:

1. Formlen for tangenten gennen (2,f(2)) er: y = f´(2)·(x-2) + f(2).

   f´(x) = 3·x² - 16·x + 3. Dette giver følgende ligning for tangenten gennem (2,f(2)):

   y = (3·2² - 16·2 + 3)·(x - 2) + 2³ - 8·2² + 3·2 + 2 ⇔

   y = -17x + 18

Svar på opgave 7:

1. Man opretter lister med antal år efter 2010 og antal hunde i tusinder. Dette gøres her i Ti-Nspire:

   årstal:={2010,2011,2012,2013,2014,2015}-2010 ▸ {0,1,2,3,4,5}

   antal:={411,449,487,524,560,584} ▸ {411,449,487,524,560,584}

   Man bruger kommandoen: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Lineær regression...(mx + b) og vælger listerne, som man har oprettet. Man får følgende resultat:

   LinRegMx årstal,antal,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Lineær regression (mx+b)"]
   ["RegEqn","m*x+b"]
   ["m",35.2857]
   ["b",414.286]
   ["r²",0.995587]
   ["r",0.997791]
   ["Resid","{...}"]]

   (Regressionsfunktionen kan udskrives: f1(x) ▸ 35.2857*x+414.286).

   Heraf ses at, a = 35,3 og b = 414, idet Ti-Nspire bruger m i stedet for a som i opgaven.

2. Tallet a er den årlige tilvækst i antallet af hunde i Danmark målt i tusinder.

Svar på opgave 8:

1. Man kan opstille følgende model

   f(x) = 4500·(1,05)^x, hvor f(x) er antallet af individer, x er antal måneder siden start, 4500 er antallet af individer fra start og 1,05 er fremskrivningsfaktoren = 1 + den månedlige vækstrate.

2. Formlen for fordoblingstiden er ln(2) /ln(a), hvor a er fremskrivningsfaktoren.

   Man får: ln(2)/ln(1,05) = 14,2.

   Dvs. fordoblingstiden er 14,2 måneder

Svar på opgave 9:

1. Man bruger en cosinusrelation til at finde |BC|, der kaldes x. Dette løses i Ti-Nspire:

   solve(cos(40.°)=(5²+7²-x²)/(2*5*7) and x>0,x) ▸ x=4.51408

   Dvs. |BC| = 4,51

2. Arealet er 0,5·h·g, hvor h er højden af trekant BDC og g er grundlinjen.

   h = |AB|·sin(40°) = 3,2139.

   g = |CD| = |BC| = 4,5141. Dette er vist nedenunder:

   

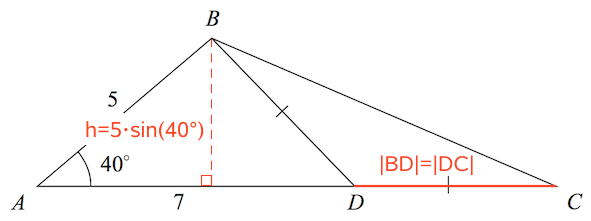
   Arealet af BDC er 0,5·3,2139·4,5141 = 7,25

Svar på opgave 10:

1. Man opretter funktionen og tegner den i Ti-Nspire:

   f(x):=4378449*exp(−15.43*exp(−0.384*x)) ▸ Udført

   

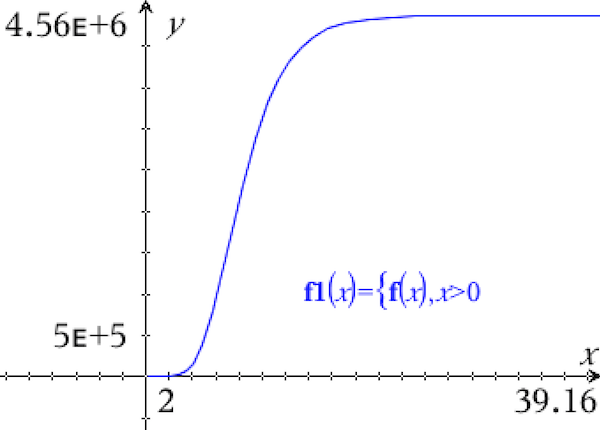
2. Antallet af artikler i 2003 er f(3):

   f(3) ▸ 33398.3

   Dvs. der er 33398 artikler i 2003

   Man skal løse ligningen f(x) = 500000 med hensyn til x. Dette tal lægges til 2000 for at få årstallet.

   solve(f(x)=500000,x) ▸ x=5.1085

   Dvs. det år, hvor 500000 artikler overstiges, er 2006

   (Prøve: f(5) = 455914 og f(6) = 937889. Dvs. når man regner med hele år, så er svaret 2006. Regner man med decimaltal, så er svaret 2005).

3. f´(10) er ændringen pr. måned i 2010. Værdien af f´(10) beregnes i Ti-Nspire:

   derivative(f(x),x)|x=10 ▸ 400216

   Dvs. ændringen pr. måned i 2010 er 400216 artikler

Svar på opgave 11:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=x²-8*ln(x) ▸ Udført

   Man løser laver en fortegnsundersøgelse for f(x). Først løses ligningen: f´(x) = 0:

   solve(derivative(f(x),x)=0 and x>0,x) ▸ x=2

   Dernæst undersøger man fortegn for f´(x) på begge sider af x = 2:

   derivative(f(x),x)|x=1 ▸ −6

   derivative(f(x),x)|x=3. ▸ 3.33333

   Dette viser, at der gælder følgende monotoniforhold for f(x):

   f(x) er aftagende for 0 < x < 2 og voksende for x > 2

Svar på opgave 12:

1. De 100 balloner er stikprøven, mens partiet (af ukendt størrelse) er populationen.

2. Nulhypotesen er, at der er lige mange af hver farve ballon i partiet.

   Det forventede antal balloner af hver farve er 100/5 = 20, hvis der skal være lige mange af hver.

   Man laver en Chi-i-anden goodness of fit test.

   Testsstørrelse: ((20-20)²+(28-20)²+(21-20)²+(13-20)²+(18-20)²)/20. ▸ 5.9

   Der er 4 frihedsgrader = antal farver minus 1.

   Den kritiske værdi beregnes i Ti-Nspire: solve(χ²Cdf(x,∞,4)=0.05,x) ▸ x=9.48773

   Da teststørrelsen er mindre end den kritiske værdi, så accepteres nulhypotesen.

   Nedenunder er den kritiske værdi beregnet i Geogebras sandsynligheds-lommeregner som alternativ til Ti-Nspire:

   

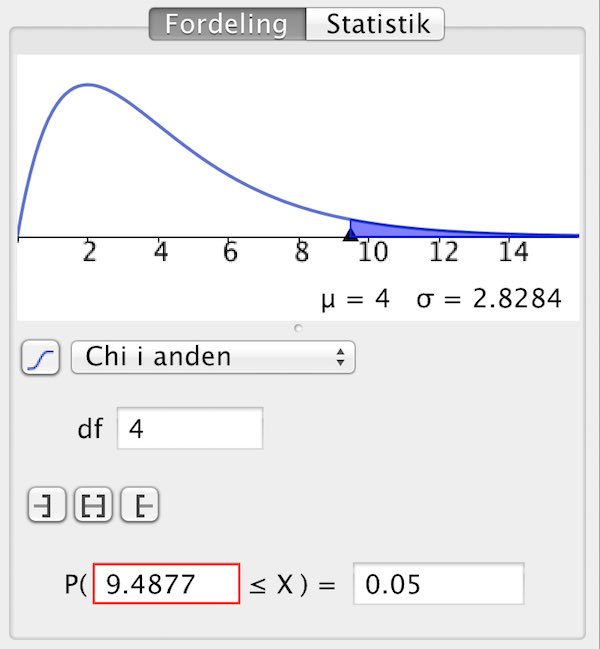
Svar på opgave 13:

1. Arealet under kurven er integralet af f(x) mellem nulpunkterne for f(x).

   Man opretter f(x) i Ti-Nspire:

   f(x):=−x²+6*x ▸ Udført

   Dernæst findes nulpunkterne:

   solve(f(x)=0,x) ▸ x=0 or x=6

   Dvs. man skal integrere f(x) fra x=0 til x=6:

   integral(f(x),x,0,6) ▸ 36

   Dvs. arealet af M er 36

2. En tredjedel af arealet af M er 36/3 = 12.

   Man skal løse ligningen F(k) = 12 for 0<k< 6. F(k) er en stamfunktion til f(k).

   Man finder F(k): integral(f(k),k) ▸ 3·k²-k³/3

   Dernæst løses F(k) = 12 (0<k<6) med hensyn til k:

   solve(3*k²-k³/3=12 and 0<k<6,k) ▸ k=2.32178

   Dvs. k = 2,322