Svar på opgave 1:

1. 5x + 7 = 2x - 2 ⇒

   5x + -2x = -2 - 7 ⇒

   3x = -9 ⇒

   x = -3

Svar på opgave 2:

1. Når der sker et fald med et bestemt antal om året (og ikke med en bestemt procentsats om året) er der tale om negativ lineær vækst eller en negativ lineær udvikling. Modellen bliver:

   f(x) = -54x + 1512, x > 0

   Her er f(x) antallet af fastnettelefoner, x er antal år efter 2010, -54 er det årlige fald i antallet af fastnettelefoner og 1512 er begyndelsesværdien, dvs. antallet af fastnettelefoner i år 2010.

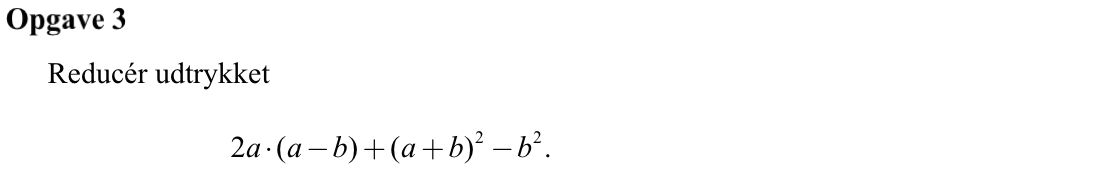
Svar på opgave 3:

1. 2a·(a - b) + (a + b)² - b² =

   2a² - 2ab + a² + 2ab + b² - b² =

   2a² + a² =

   3a²

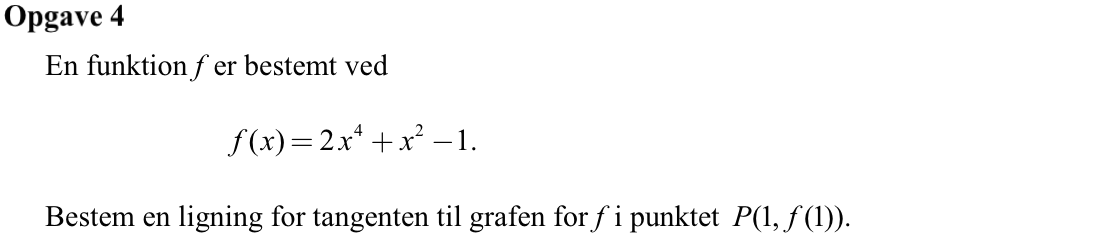
Svar på opgave 4:

1. Tangentens ligning er y = f´(1)·(x - 1) + f(1).

   f´(x) = 8x³ + 2x ⇒ f´(1) = 8·1³ + 2·1 = 10.

   f(1) = 2·1⁴ + 1² - 1 = 2. Dette giver ligningen:

   y = 10·(x - 1) + 2 ⇒ y = 10x - 8

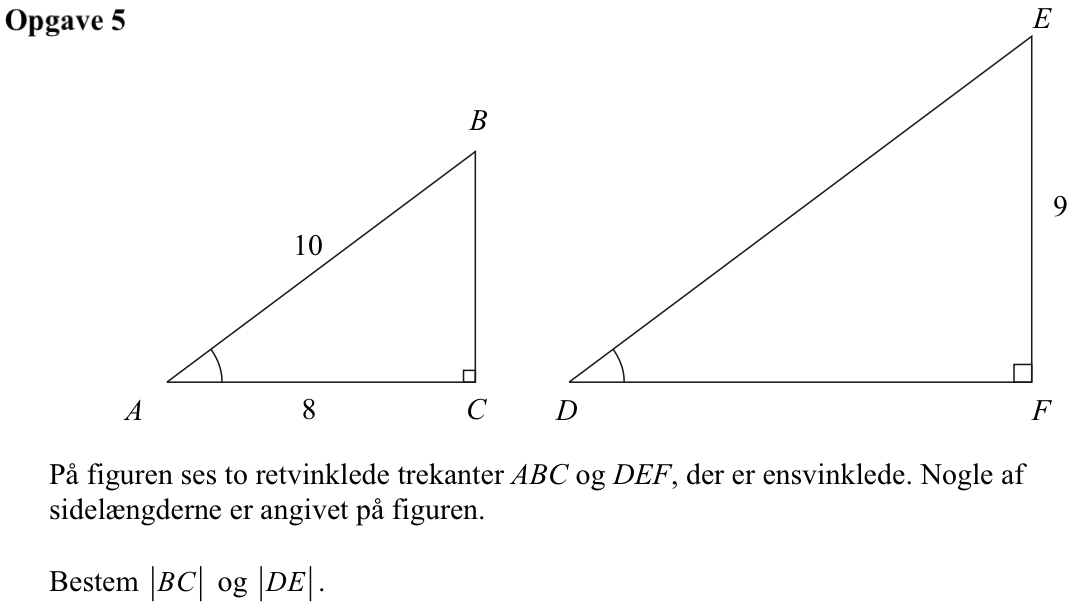
Svar på opgave 5:

1. |BC| er katete i en retvinklet trekant. Den findes ved hjælp af Pythagoras læresætning:

   |BC|² + 8² = 10² ⇒

   |BC|² = 10² - 8² ⇒

   |BC|² = 100 - 64 ⇒

   |BC|² = 36 ⇒

   |BC| = √36 ⇒

   |BC| = 6

   Skaleringsfaktoren mellem trekant ABC og trekant DEF er |EF|/|BC| = 9/6 = 1,5.

   Dermed er |DE| = 1,5·|AB| = 1,5·10 = 15

Svar på opgave 6:

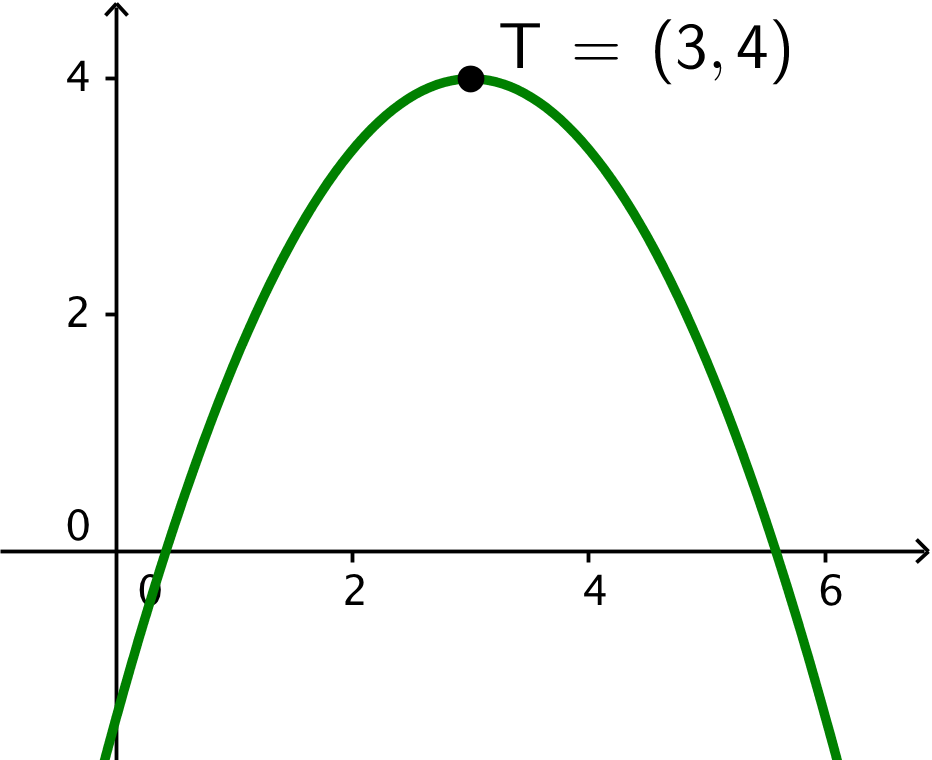
1. Grafen for andengradspolynomiet er en parabel. At c < 0 betyder, at parablen skærer den negative del af y-aksen. Når toppunktet samtidig har en positv y-værdi, betyder det at parablens grene vender nedad.

   En mulig graf er tegnet nedenunder i Geogebra:

   

Svar på opgave 7:

1. Man opretter to lister: en for antal år efter 2013 og en for årsomsætningen.

   antalår:={2013,2014,2015}-2013 ▸ {0,1,2}

   årsomsætning:={4.5,19,71} ▸ {4.5,19,71}

   Man bruger kommandoen:

   Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Exponentiel regression... og vælger listerne, som man har oprettet. Man får resultatet:

   ExpReg antalår,årsomsætning,1: CopyVar stat.RegEqn,f1: stat.results

   

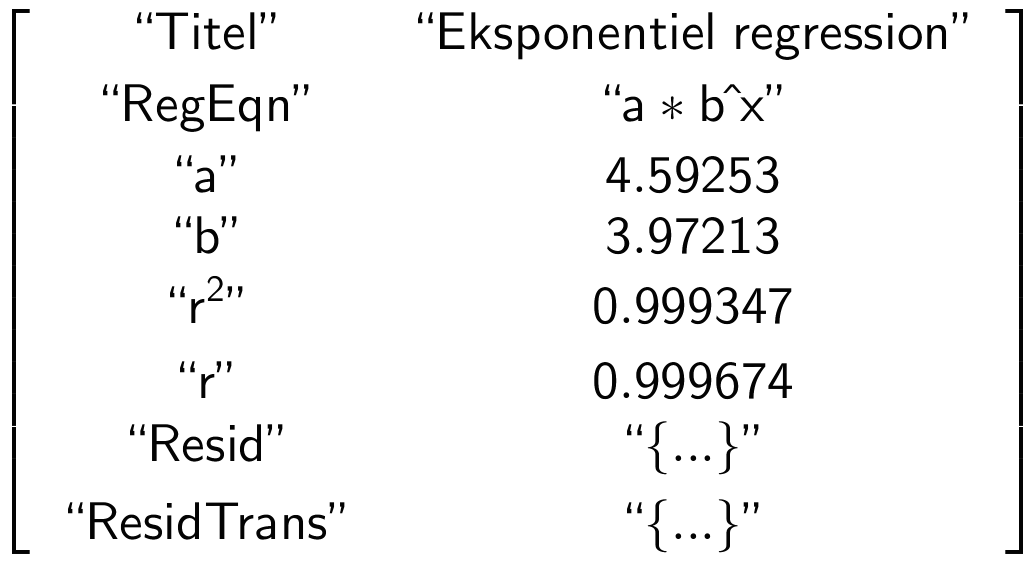
   Idet det bemærkes, at Ti-Nspire bruger a og b modsat opgaven får man:

   a = 3,972 og b = 4,593

2. Tallet a er fremskrivningsfaktoren. Det er det tal som man ganger det gamle års omsætning med for at få det nye.

3. Årsomsætningen i 2016 er f(2016-2013) = f(3) = 4,593·3,972³ mia. kr. = 287,8 mia. kr.

   Fordoblingstiden er ln(2)/ln(a) år = ln(2)/ln(3,972) år = 0,50 år

Svar på opgave 8:

1. Man oprettter en liste over aldergrænser. Man starter med den nedre grænse for første intaervel og fortsætter derefter med øvre grænser for hvert interval.

   kvindernesalder:={15,20,25,30,35,40,45,50} ▸ {15,20,25,30,35,40,45,50}

   Man opretter en liste over antallet af kvinder i hvert interval:

   antalkvinder:={0,2206,4105,3018,2541,2162,954,87} ▸ {0,2206,4105,3018,2541,2162,954,87}

   Ud fra sidste liste laver man en liste over kummulerede frekvenser:

   kummuleretfrekvens:=cumulativeSum(antalkvinder/sum(antalkvinder))*1. ▸ {0.,0.1464,0.4187,0.6189,0.7875,0.9309,0.9942,1.}

   Ud fra listerne kvindernesalder og kummuleretfrekvens fremstiller man nedenstående sumkurve i Ti-Nspire.

   

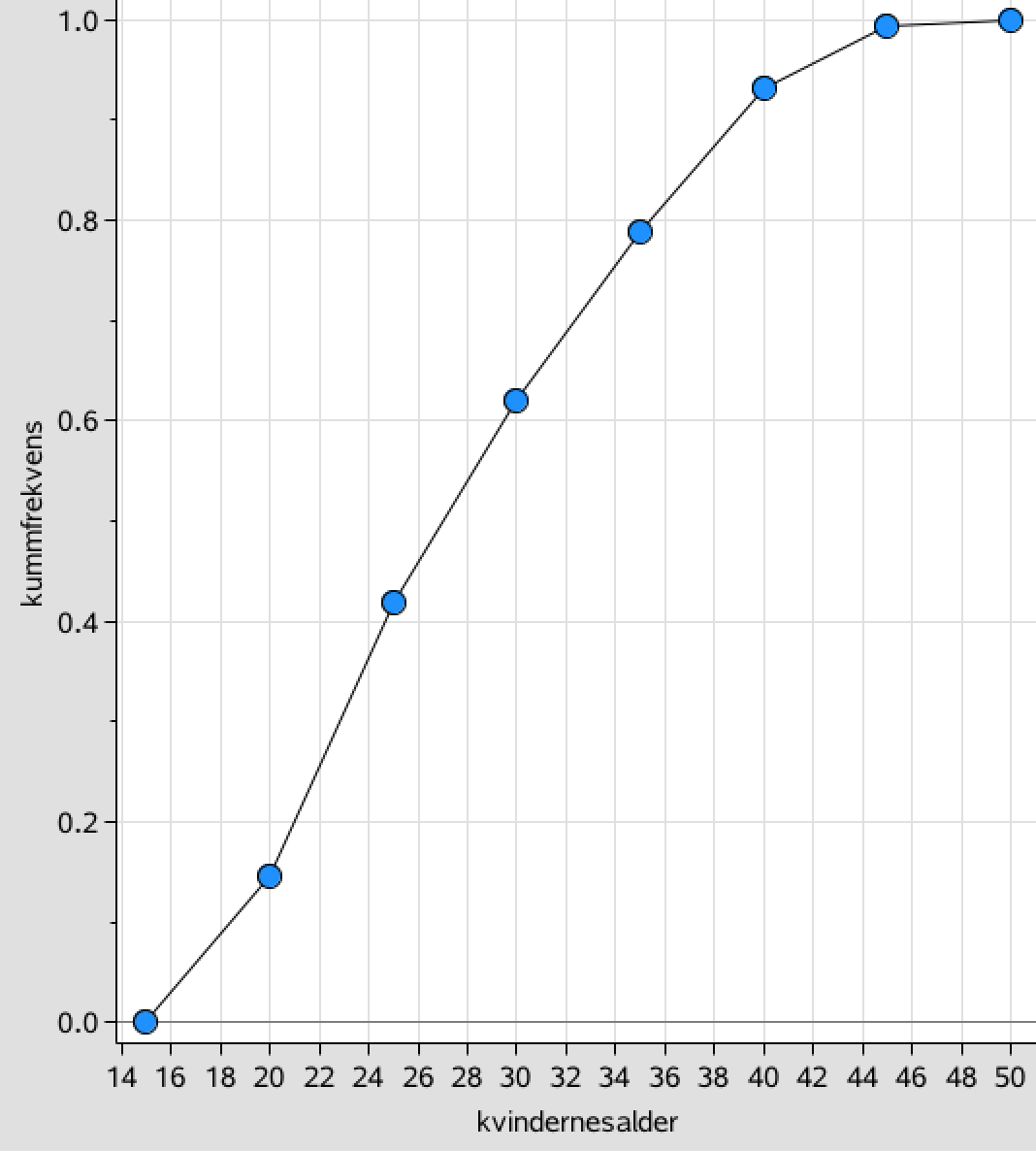
2. De vandrette linjers skæring med kurven ovenfor markerer kvartilerne. Af førstekoordinaterne til skæringspunkterne på ovenstående graf aflæses kvartilsættet til:

   

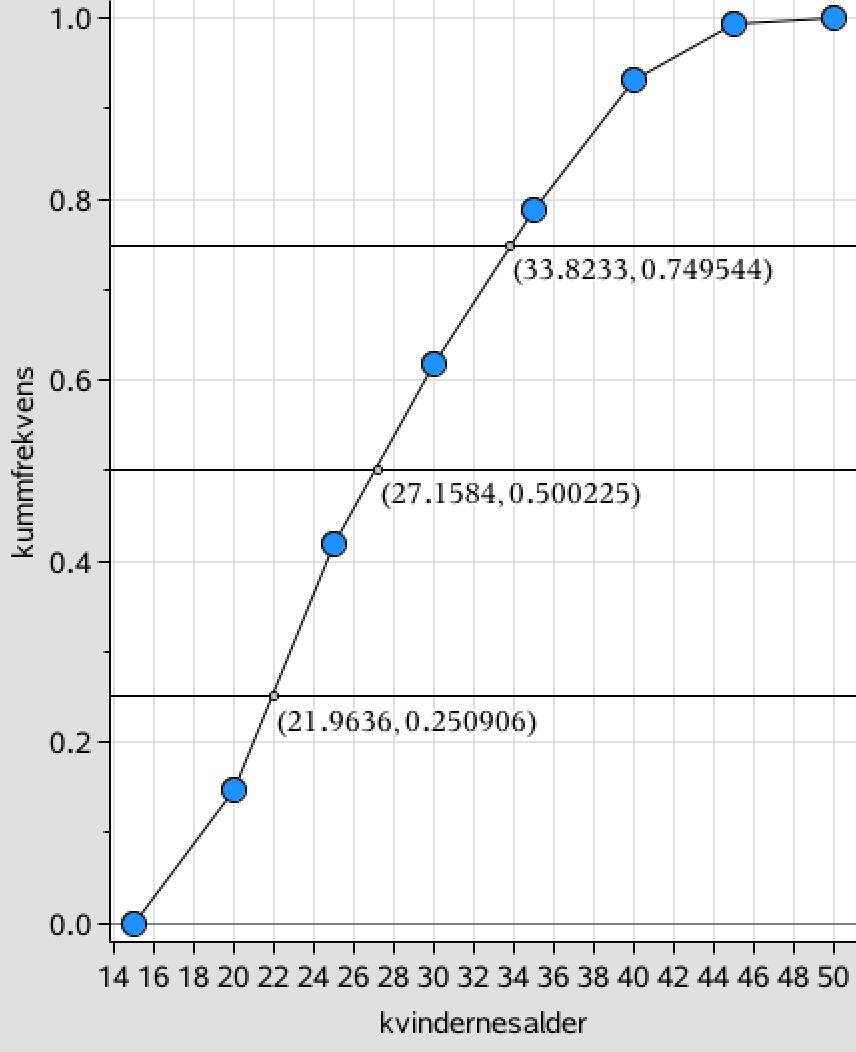
   Nedre kvartil = 22,0 år, median = 27,2 år og øvre kvartil = 33,8 år

   Den andel af kvinderne som er 32 år eller derunder og som har fået foretaget en abort aflæses på sumkurven til 0,68 = 68 %.

   

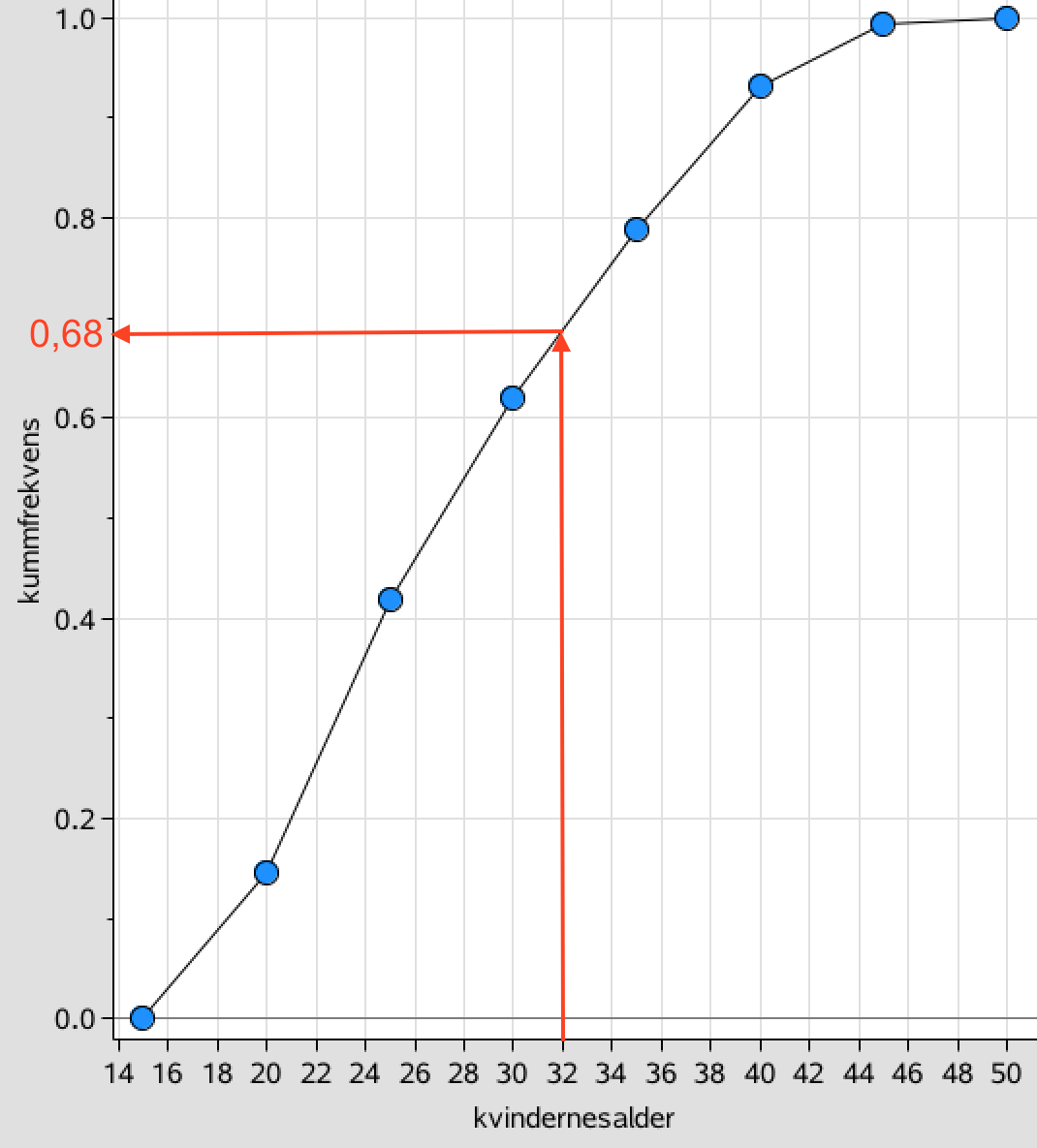
   Dette tal skal trækkes fra 100 % for at få den procentdel af kvinder på mere end 32 år som har fået foretaget en abort.

   Dvs. andelen af kvinder på mere end 32 år, som har fået foretaget en abort er 100 % - 68 % = 32 %

Svar på opgave 9:

1. m(t) oprettes i Ti-Nspire:

   m(t):=(9-0.625*t)² ▸ Udført

   Dernæst finder man maveindholdet efter 6 timer som m(6):

   m(6) ▸ 27.5625

   Dvs. at maveindholdet efter 6 timer er 27,6 g

2. Man skal løse ligningen m(t) = 0 med hensyn til t.

   solve(m(t)=0,t) ▸ t=14.4

3. m´(1) findes i Ti-Nspire med kommandoen:

   derivative(m(t),t)|t=1 ▸ −10.46875

   Dette tal -10,47 betyder, at efter en time mindskes fiskens maveindhold med en hastighed af 10,47 g/t

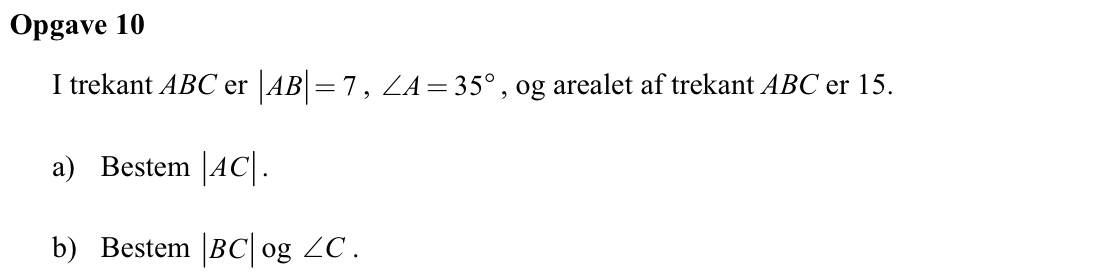
Svar på opgave 10:

1. Man starter med at beregne højden i trekanten. Det gør man med den trigonometriske formel: højde i B = |AB|·sin(∠) = 7·sin(35°) = 4,015.

   Ud fra højden i B og arealet af trekant ABC kan længden af grundlinjen |AC| beregnes: areal = 0,5·højde·grundlinje ⇒ 15 = 0,5·4,015·|AC| ⇒

   15/(0,5·4,015) = |AC| ⇒ |AC| = 7,4719 = 7,47

2. Man finder |BC| ved hjælp af en cosinusrelation:

   solve(cos(35.°)=(7²+7.47191²-x²)/(2*7*7.47191),x)|x>0 ▸ x=4.375

   Dvs. |BC| = 4,375

   ∠C findes ligeledes med en cosinusrelation:

   solve(cos(x*1.°)=(7²+4.375²-7.47191²)/(2*7*4.375),x)|0<x<180 ▸ x=78.40

   Dvs. ∠C = 78,4°

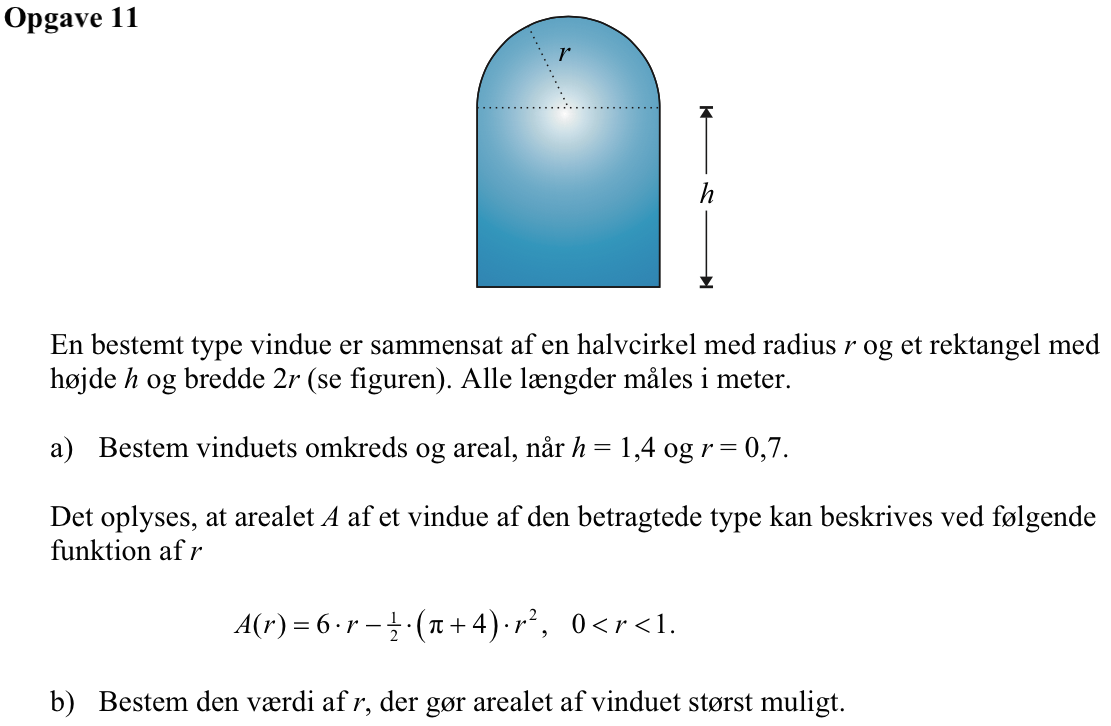
Svar på opgave 11:

1. Omkredsen er π·r + 2·r + 2·h = 6,399 = 6,40

2. Standardmetode:

   Man opretter A(r):

   a(r):=6*r-0.5*(π+4)*r^(2) ▸ Udført

   Man differentierer A(r). Den afledte funktion kaldes A_m(r):

   a_m(r):=derivative(a(r),r) ▸ Udført ...den afledte funktion til A(r) oprettes

   solve(a_m(r)=0,r) ▸ r=0.840149 ...find nulpunkter for den afledte funktion

   a_m(0.8) ▸ 0.286726 ...lav fortegnsundersøgelse for afledte funktion før nulpunkt

   a_m(0.9) ▸ −0.427433 ...lav fortegnsundersøgelse for afledte funktion efter nulpunkt

   Nulpunkts- og fortegnsundersøgelsen for den afledte funktion af A(r) viser, at r = 0,84 er et maksimum. Da der kun er eet, så er det et globalt maksimum.

   Dermed antager vinduets sit maksimale areal for r = 0,84

   Alternativ metode i Ti-Nspire:

   Man bruger kommandoen fMax til af finde det r, der giver det største areal i intervallet 0 < r < 1.

   fMax(a(r),r)|0<r<1 ▸ r=0.8401

   Dvs. det største areal af vinduet fås for r = 0,84

Svar på opgave 12:

1. Man laver grafen i Geogebra som vist nedenunder.

   

   Man opretter f(x) i Ti-Nspire:

   f(x):=0.000134*x³-0.00912*x²+0.567*x ▸ Udført

   Man skal beregne f(20) og får:

   f(20) ▸ 8.764

   Dvs. den 20 % fattigste del af befolkningen tjener 8,8 % af den samlede indkomst

2. Man beregner G med følgende kommando i Ti-Nspire:

   100-0.02*integral(f(x),x,0,100) ▸ 37.1

   Dvs. indkomstuligheden i landet er 37 %