Svar på opgave 1:

1. 3x + 6 = -x + 2 ⇒

   3x + x = 2 - 6 ⇒

   4x = -4 ⇒

   x = -1

Svar på opgave 2:

1. Man skal undersøge om f(2) er lig med 10.

   f(2) = 2² + 3·2 = 4 + 6 = 10

   Dvs. punktet (2,10) ligger på grafen for f

Svar på opgave 3:

1. De 5000 er det oprindelige beløb eller startkapitalen.

   1,03 er fremskrivningsfaktoren eller det tal som kan skal gange det indestående beløb med hver termin for at få det nye indestående beløb.

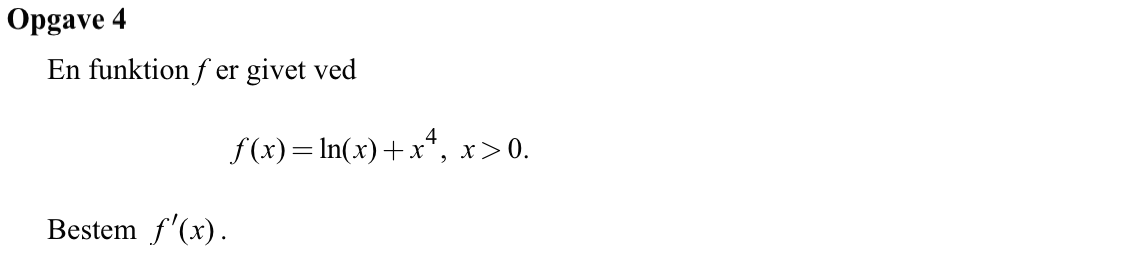
Svar på opgave 4:

1. f´(x) = 1/x + 4x³, x > 0.

Svar på opgave 5:

1. Nedenfor er graferne vist i Geogebra.

   

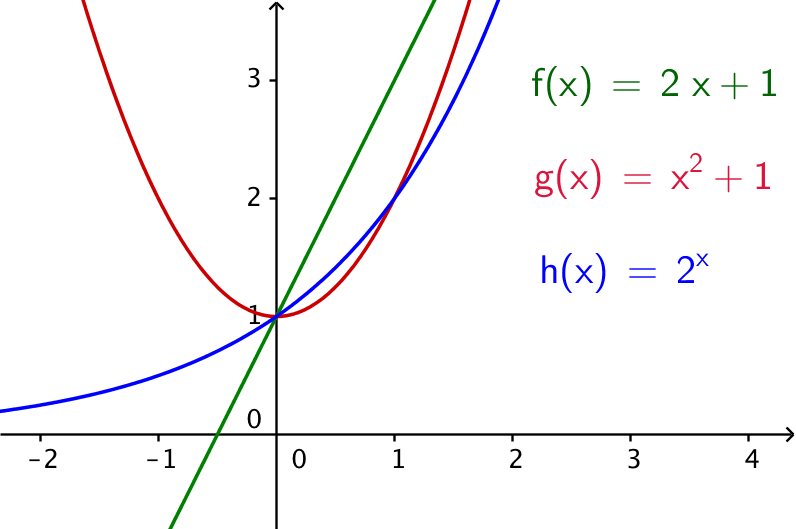
Svar på opgave 6:

1. En vilkårlig stamfunktion F(x) for f(x) er det ubestemte integrale til f(x), som giver: F(x) = 5·e^x + (1/4)·x⁴ + k.

   Man skal bestemme k så F(0) = 10, dvs. løse ligningen: 5·e⁰ + (1/4)·0⁴ + k = 10 ⇒

   5 + k = 10 ⇒

   k = 5

   Dvs. den søgte stamfunktion er F(x) = 5·e^x + (1/4)·x⁴ + 5

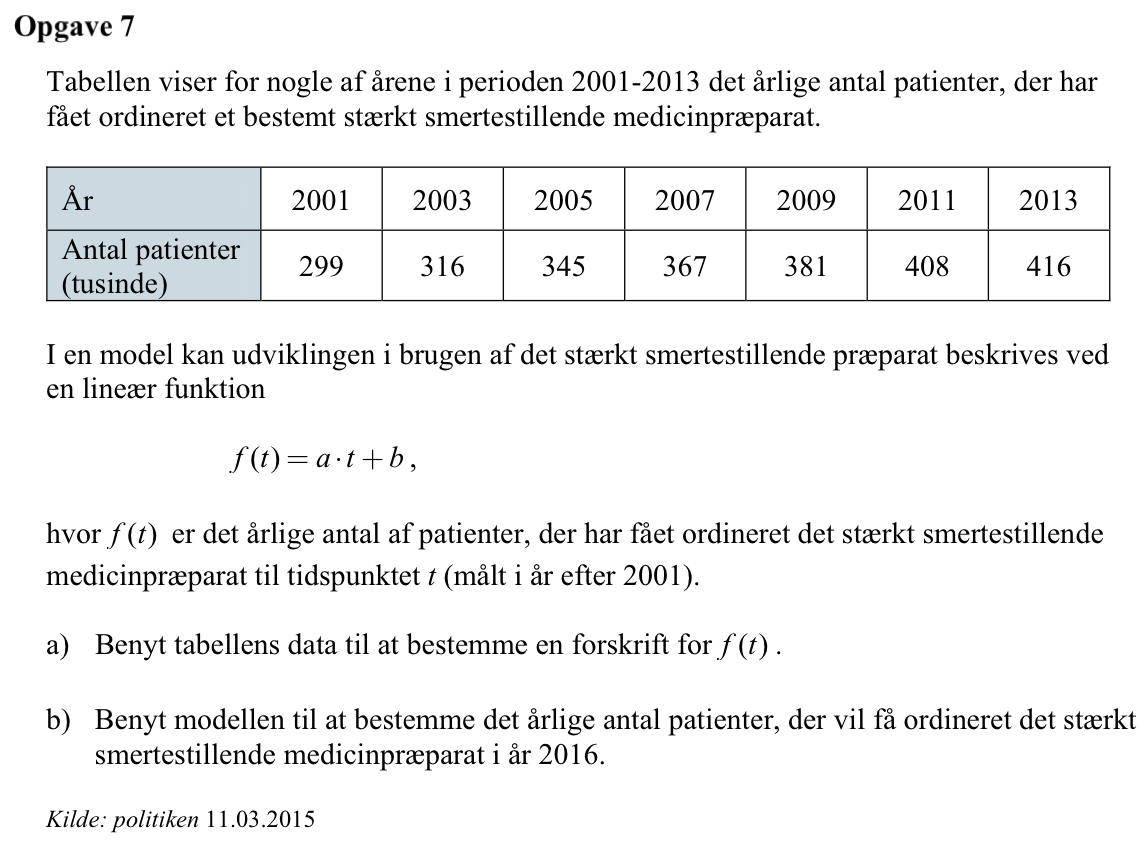
Svar på opgave 7:

Løsning i Ti-Nspire.

1. Man opretter to lister: en for antal år efter 2001 og en for antal patienter som får medicinen.

   listeår:={2001,2003,2005,2007,2009,2011,2013}-2001 ▸ {0,2,4,6,8,10,12}

   listepatienter:={299,316,345,367,381,408,416} ▸ {299,316,345,367,381,408,416}

   Man bruger kommandoen:

   Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Lineær regression (mx+b)... og vælger listerne, som man har oprettet. Man får resultatet:

   LinRegMx listeår,listepatienter,1: CopyVar stat.RegEqn,f1: stat.results

   

   f(t) = 10,20·t + 300,54

2. Man skal finde f(2016-2001) = f(15) = 10,20·15 + 300,54 = 453,5

Svar på opgave 8:

1. Man bruger formlen for procent-procentvækst for en potensfunktion.

   Den procentvise vækst = (1 + 15 %)^0,425 - 1 = 1,15^0,425 - 1 = 0,0612 = 6,12 %

Svar på opgave 9:

1. Man opretter en liste med intervalgrænser. Den medtager nedre grænse i første interval og dernæst den øvre grænse i hvert interval.

   længde:={18,20,22,24,26,28,30,32} ▸ {18,20,22,24,26,28,30,32}

   Dernæst oprettes en liste med antallet af sild i hvert interval.

   listeantal:={0,5,10,15,16,20,18,10} ▸ {0,5,10,15,16,20,18,10}

   Udfra den sidste liste beregnes en liste over kummulerede frekvenser for vægten af høstsild.

   kummuleretfrekvens:=(cumulativeSum(listeantal)/sum(listeantal))*1. ▸ {0.,0.0532,0.1596,0.3191,0.4894,0.7021,0.8936,1.}

   Nedenunder er sumkurven tegnet i Ti-Nspire.

   

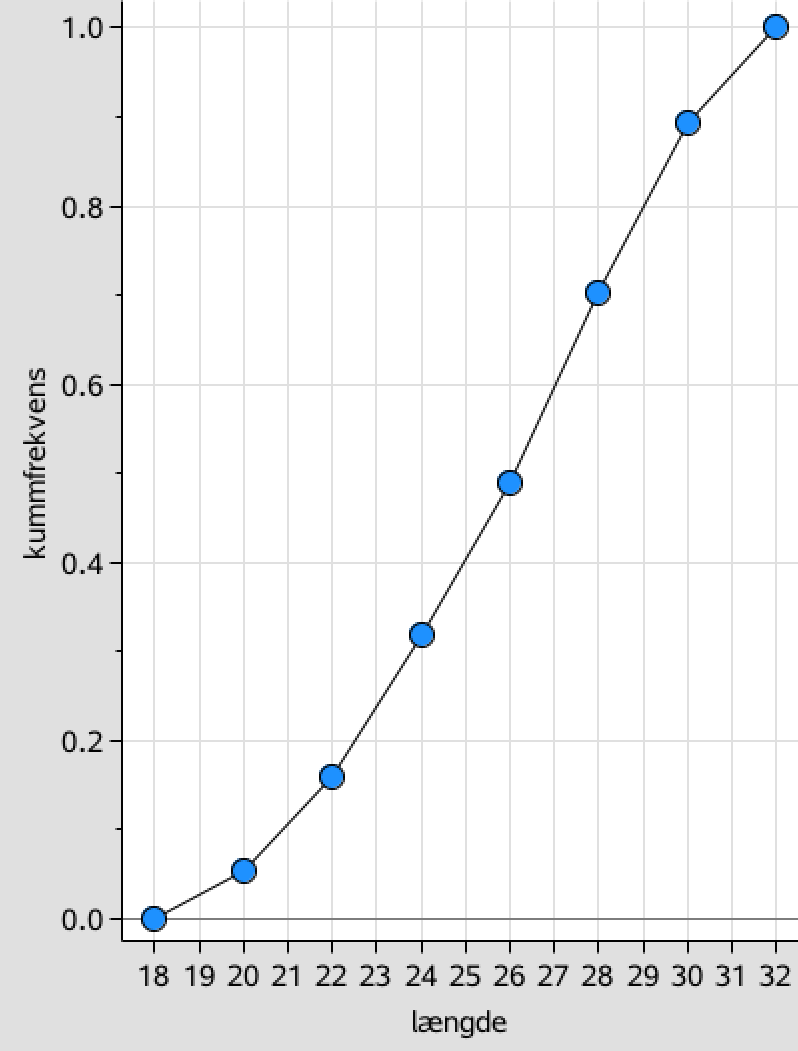
   Nedenunder er linjerne for frekvenserne 0,25; 0,5 og 0,75 indtegnet. Derer skæringspunkter med sumkurven er markeret.

   

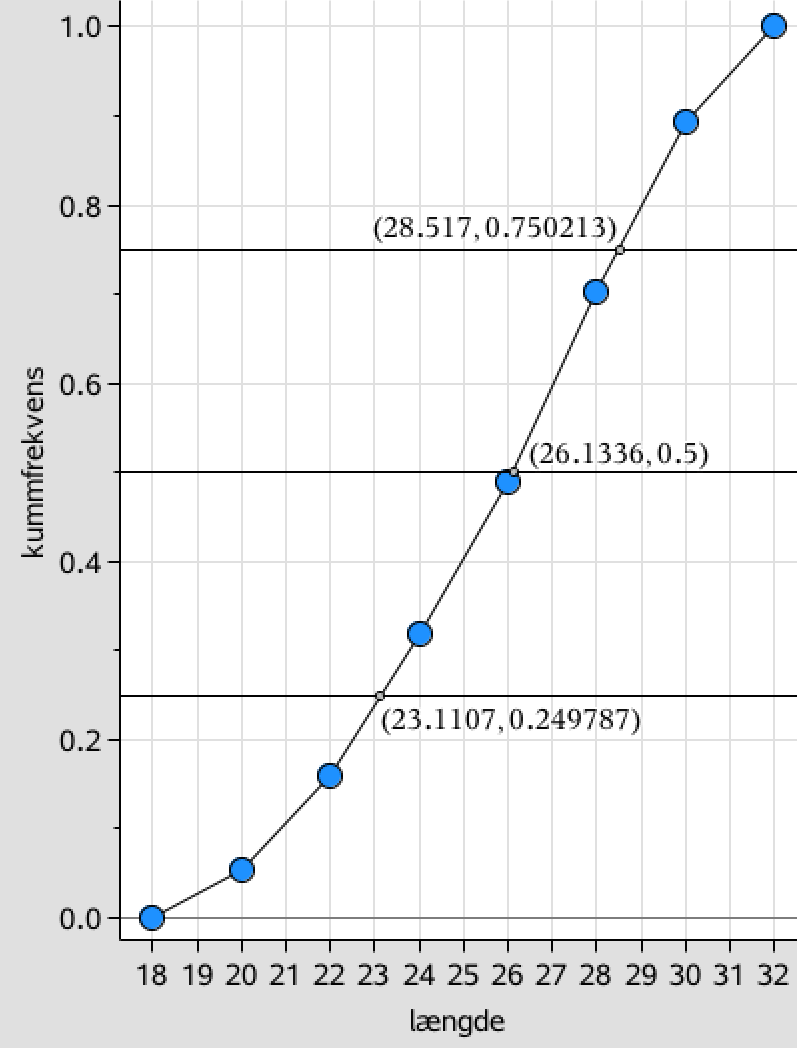
   Af kurven fremgår det, at kvartilsættet for længdefordelingen af høstsild er:

   Nedre kvartil = 23,2 cm, median = 26,1 cm og øvre kvartil = 28,6 cm

2. Længden af sildene er spredt over et større interval og generelt er de mindre.

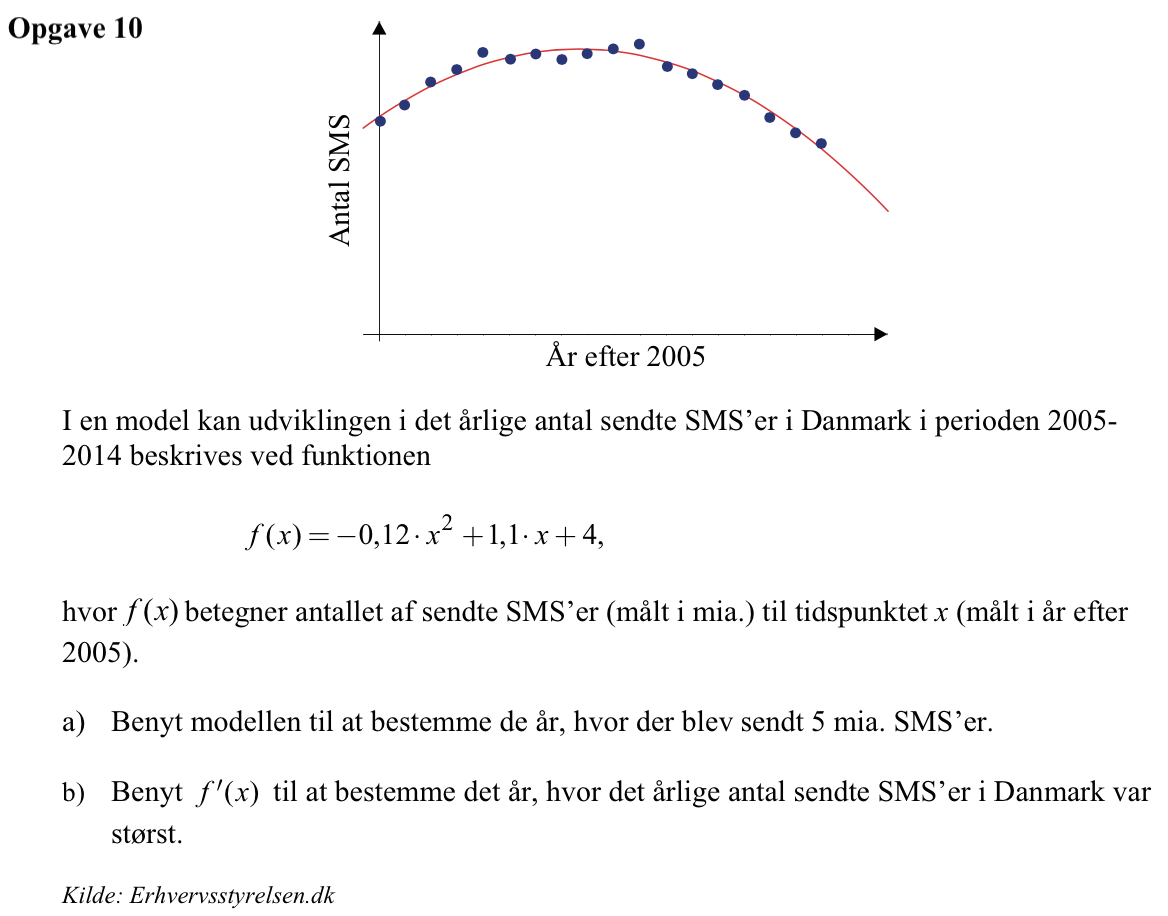
Svar på opgave 10:

1. Man opretter f(x) i Ti-Nspire kommandoen: f(x):=−0.12*x^(2)+1.1*x+4 ▸ Udført

   Man bruger solve-kommandoen til at løse uligeheden f(x) > 5

   solve(f(x)>4,x) ▸ 0.<x<9,1667

   Dvs. antallet af SMS'er var over 5 mia. mellem 2005 og 2014

2. Man løser f´(x) = 0 med hensyn til x ved hjælp af kommandoen:

   solve(derivative(f(x),x)=0,x) ▸ x=4.5833

   Dvs. det maksimale antal SMS'er nås i 2005 + 5 = 2010

Svar på opgave 11:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=2*x³-6*x²-12*x+1 ▸ Udført

   Tangentlinjen findes ved hjælp af "y=" + tangentLine-kommandoen i Ti-Nspire:

   y=tangentLine(f(x),x,5) ▸ y=78*x-349

   Dvs. tangentlinjen til f gennem P er y=78x-349

2. Man skal løse ulighederne f´(x) > 0 og f´(x) < 0. Man bruger solve-kommandoen i Ti-Nspire:

   solve(derivative(f(x),x)>0.,x) ▸ x<−0.732 or x>2.732

   solve(derivative(f(x),x)<0.,x) ▸ −0.732<x<2.732

   Dermed ses at f vokser for x < 0,732 aftager for −0,732 < x < 2,732 og vokser for x > 2,732

3. Man opretter g(x) i Ti-Nspire:

   g(x):=−3*x²+33 ▸ Udført

   Man finder skæringspunktet ved at løse ligninge f(x) = g(x) med hensyn til x. Man bruger solve-kommandoen i Ti-Nspire:

   solve(f(x)=g(x),x) ▸ x=4

   Koordinatsættet til Q er (4,f(4)) = (4,-15)

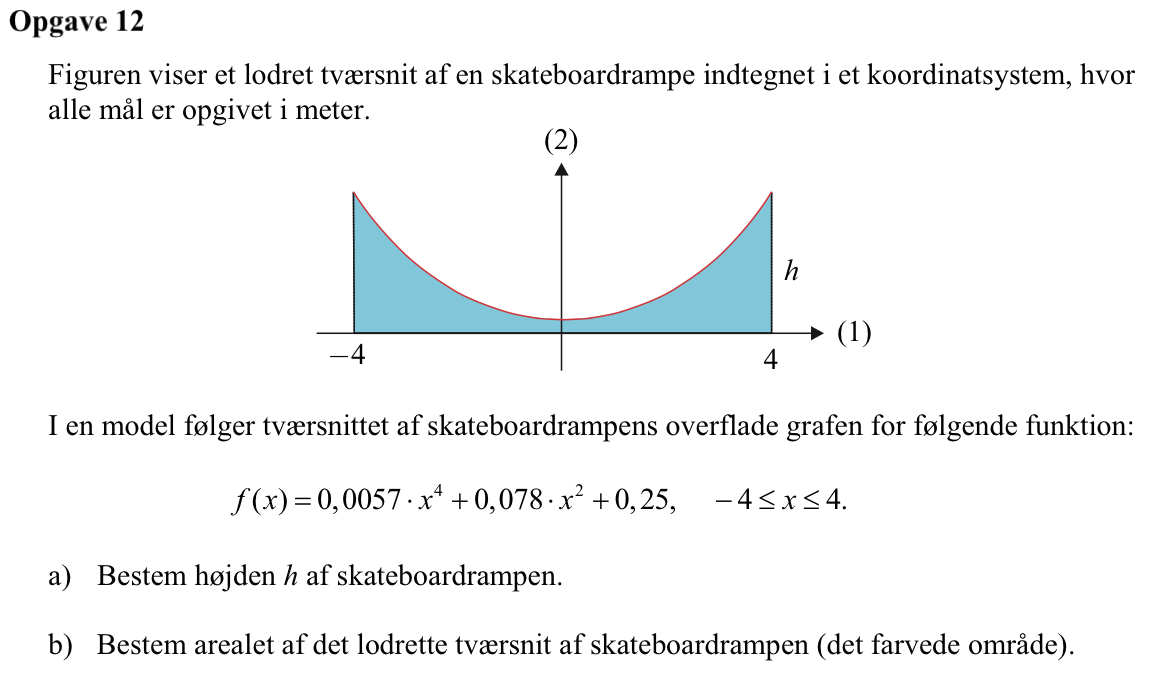
Svar på opgave 12:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=0.0057*x⁴+0.078*x²+0.25 ▸ Udført

   Højden findes i grafens endepunkter. Man finder f(4):

   f(4) ▸ 2,9572

   Dvs. højden er 2,96

2. Man skal finde det nestemte integrale af f gfra x = -4 til x = 4. Dette gøres med følgende kommando i Ti-Nspire:

   integral(f(x),x,−4,4) ▸ 7.66272

   Dvs. arealet af det blå område er 7,66

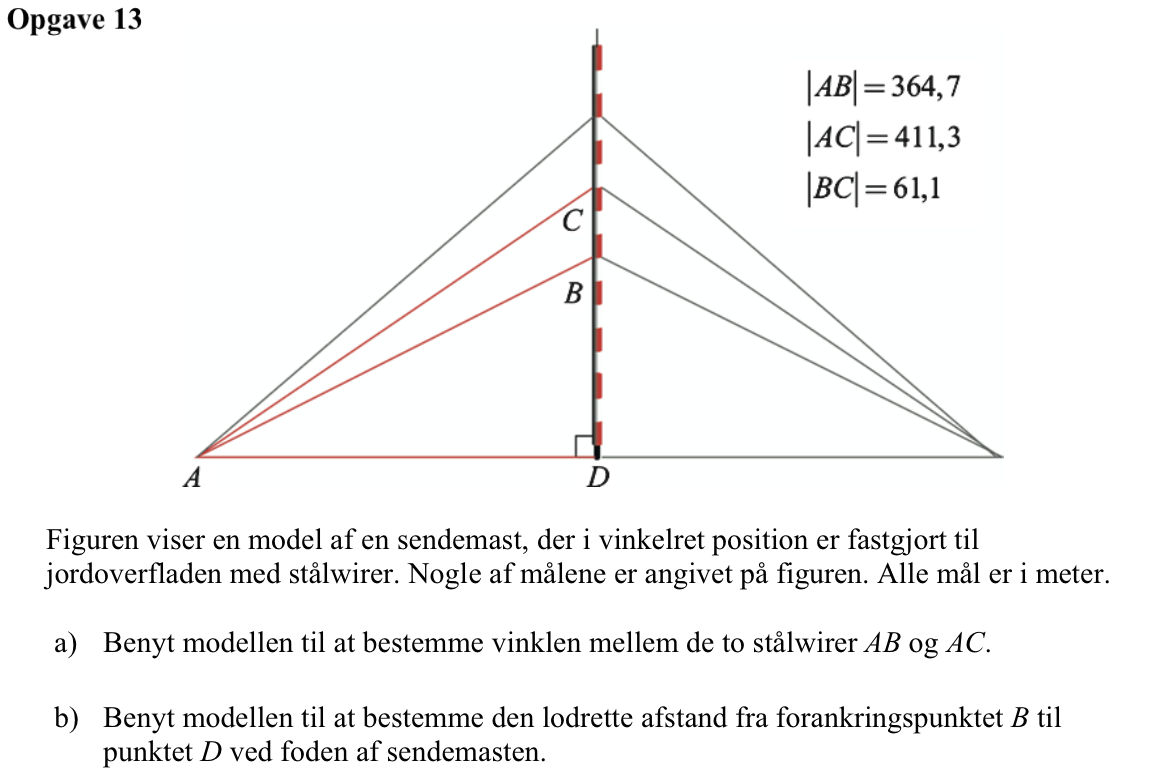
Svar på opgave 13:

1. Man kender alle sider i trekant ABC. Vinklen mellem AB og AC kaldes x og findes ved hjælp af solve-kommandoen og en cosinusrelation i Ti-Nspire:

   solve(cos(x*1.°)=(364.7²+411.3²-61.1²)/(2·364.7·411.3),x)|0<x<180 ▸ x=5.8487

   Dvs. vinklen mellem AB oc AC er 5,8°

2. Man skal finde vinklerne i trekant ACD og starter med vinkel C. Den findes ved en cosinusrealtion som i opgave a):

   solve(cos(x*1.°)=(411.3²+61.1²-364.7²)/(2·411.3·61.1),x)|0<x<180 ▸ x=37.46

   Man kender vinkel C = 37,46° og vinkel D = 90°.

   Heraf følger at vinkel DAC = 180° - (90° + 37,46°) = 52,54°.

   Herud fra kan |DC| findes ved den trigonometriske relation: |DC| = |AC|·sin(52,54°) = 411,3·0,7938 = 326,48

   Dvs. |DB| = |DC| - |BC| = 326,48 - 61,1 = 265,38