Svar på opgave 1:

1. x² + 4x + 3 = 0 ⇔

   x = -2 ± 0,5·√[16-12] ⇔

   x = -2 ± 0,5·√[4] ⇔

   x = -2 ± 0,5·2 ⇔

   x = -2 ± 1 ⇔

   x = -2 - 1 ∨ x = -2 + 1 ⇔

   x = -3 ∨ x = -1

Svar på opgave 2:

1. Linjen har grundlæggende set ligningen: y = ax + b.

   a findes som hældningen til linjen gennem P og Q:

   a = (5 - 9)/(4 - 2) = -2

   Dette giver foreløbig: y = -2x + b.

   For at finde b indsættes P's koordinater i ligningen:

   9 = -2·2 + b ⇒ 9 + 4 = b ⇒ b = 13. Dette giver den færdige ligning:

   y = -2x + 13

Svar på opgave 3:

1. Der er tale om positiv lineær vækst. Modellen er:

   f(x) = 8x + 480,

   hvor f(x) er vægten af kasse med klodser og x er antallet af klodser.

Svar på opgave 4:

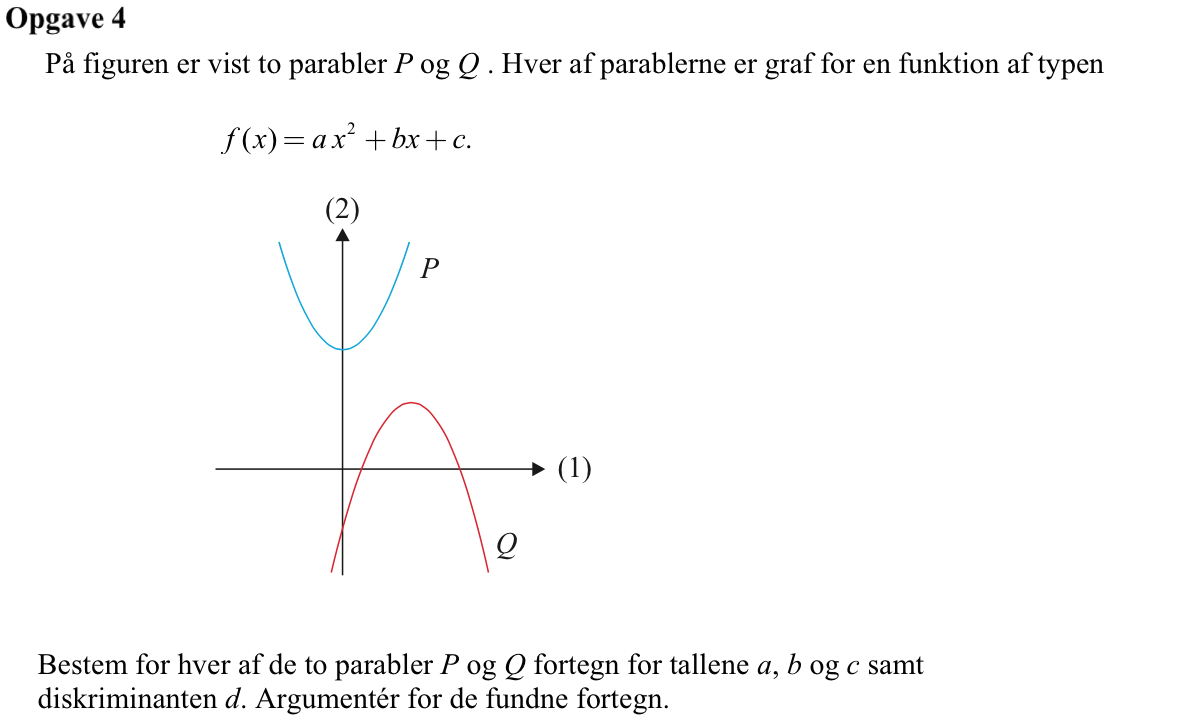
1. P:

   a > 0, da grenene vender opad,

   b = 0, da hældningen til P i dens skæringspunkt med y-aksen er 0

   c > 0, da P skærer y-aksen i dens positive del.

   d < 0, da P ikke skærer x-aksen

   Q:

   a < 0, da grenene vender nedad,

   b > 0, da hældningen til Q i dens skæringspunkt med y-aksen er positiv

   c < 0, da Q skærer y-aksen i dens negative del.

   d > 0, da Q skærer x-aksen i to punkter

Svar på opgave 5:

1. En vilkårlig stamfunktion til f kan skrives:

   F(x) = 2x³ + 2x² - 3x + k, hvor k er en reel konstant.

   Man skal bestemme k, så F(1) = 10, dvs.

   2·1³ + 2·1² - 3·1 + k = 10 ⇒

   2 + 2 - 3 + k = 10 ⇒

   k = 10 - 1 ⇒

   k = 9

   Dvs. den søgte stamfunktion er F(x) = 2x³ + 2x² - 3x + 9

Svar på opgave 6:

1. Man indfører en hjælpelinje fra C vinkelret med på AD, så der fremkommer et rektangel med siderne 4 og 8 samt en retvinklet trekant med kateterne 8 og 6.

   Dette er vist nedenunder:

   

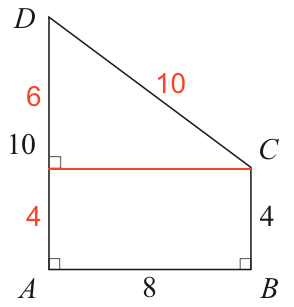
   Arealet af rektanglet er 4·8 = 32 og arealet af den retvinklede trekant er 0,5·6·8 = 24. Det samlede areal for firkant ABCD er 24 + 32 = 56

   For at finde omkredsen skal man kende hypotenusen |DC| i den retvinklede trekant. Dette gøres ved hjælp af Pythagoras læresætning:

   |BD|² = 6² + 8² ⇒ |BD| = √[36 + 64] = 10.

   Dermed er omkredsen: 10 + 10 + 4 + 8 = 32

Svar på opgave 7:

1. Man opretter en liste over intervalgrænser for længden af gulerødderne i Ti-Nspire. Man vælger nedre grænse for første interval som første element og derefter den øvre grænse for hvert interval.

   længde:={155,160,165,170,175,180,185} ▸ {155,160,165,170,175,180,185}

   Man opretter derefter en liste over hyppigheder, idet man indsætter et 0 forrest svarende til, at man indsatte nedre grænse for første interval i listen over interval grænser.

   hyppighed:={0,2,6,8,9,11,6} ▸ {0,2,6,8,9,11,6}

   Til sidst laver man en liste over kummulerede frekvenser ud fra listen over hyppigheder.

   kummfrekvens:=cumulativeSum(hyppighed/sum(hyppighed))*1. ▸ {0.,0.047619,0.190476,0.38095,0.5952,0.85714,1.}

   Listen over kummulerede frekvenser skrives som "(interval): kummuleret frekvens":

   (-155): 0; (155-160): 0,048; (160-165): 0,190; (165-170): 0,381; (170-175): 0,595;

   (175-180): 0,857; (180-185): 1.

2. Nedenunder er sumkurven tegnet i Ti-Nspire:

   

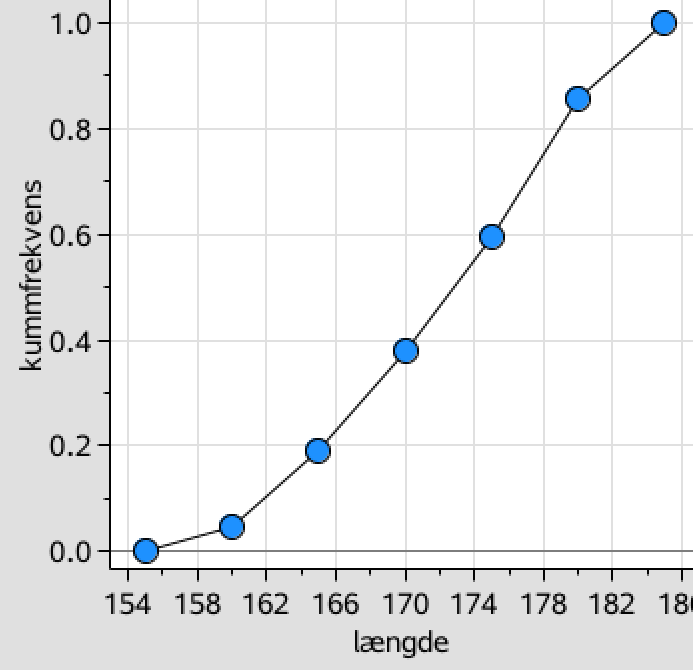
   Nedenunder er kvartilsættet beregnet ud fra sumkurven. Vandrette linjer er tegnet ud fra frekvenserne 0,25; 0,50 og 0,75.

   x-koordinaterne til deres skæringspunkter med sumkurven giver kvartilsættet.

   

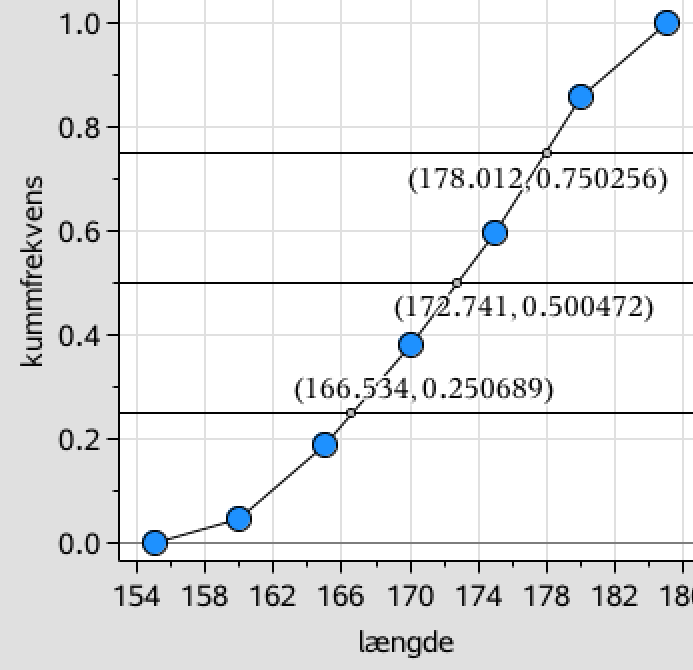
   Kvartilsættet er: nedre kvartil = 167, median = 173 og øvre kvartil = 178

Svar på opgave 8:

1. Man oprettter en liste over år efter 2010 i Ti-Nspire.

   årstal:={2010,2011,2012,2013,2014}-2010 ▸ {0,1,2,3,4}

   Dernæst opretter man en liste over datatrafik år for år:

   datatrafik:={6533,11344,19415,30871,50727} ▸ {6533,11344,19415,30871,50727}

   Man bruger kommandoen Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Lineær regression (mx + b)... og får:

   ExpReg årstal,datatrafik,1: CopyVar stat.RegEqn,f1: stat.results ▸

   

   Værdier ne af a og b fremgår af resultatlisten bare byttet om i forhold til opgaven.

   Det ses at a = 1,6653 og b = 6722,9

   Man kan også bruge den regressions-funktion, der hedder f1(x), som Ti-Nspire selv opretter.

   f1(x) ▸ 6722.85*1.66534^x

   Heraf kan a og b aflæses til det samme som før.

2. Den forventede datatrafik i 2016 beregnes i Ti-Nspire som f(2016 - 2010) = f(6):

   f1(2016-2010) ▸ 143408.9

   Dvs. mængden af datatrafik i 2016 forventes at være 143409 TB

   Grundtallet a er fremskrivningsfaktoren, dvs. det tal, man hvert år skal gange det gamle års

   datamængde med for at få det nye års datamængde.

3. Fordoblingstiden bergnes som ln(2)/ln(a):

   ln(2)/ln(1.66534) ▸ 1.359

   Dvs. fordoblingstiden er 1,4 år

Svar på opgave 9:

1. Man beregner først vinkel C ved hjælp af reglen om, at summen af vinklerne i en trekant er 180°: Vinkel C = 180° - 47° - 58° = 75°.

   Dernæst beregnes |AC| = x ved hjælp af en sinusrelation

   solve(x/sin(58.°)=73/sin(75.°),x) ▸ x=64.09137

   Dvs. |AC| er 64,1 m

2. Nedenfor er brøndenes indbyrdes placeringen tegnet i Geogebra:

   

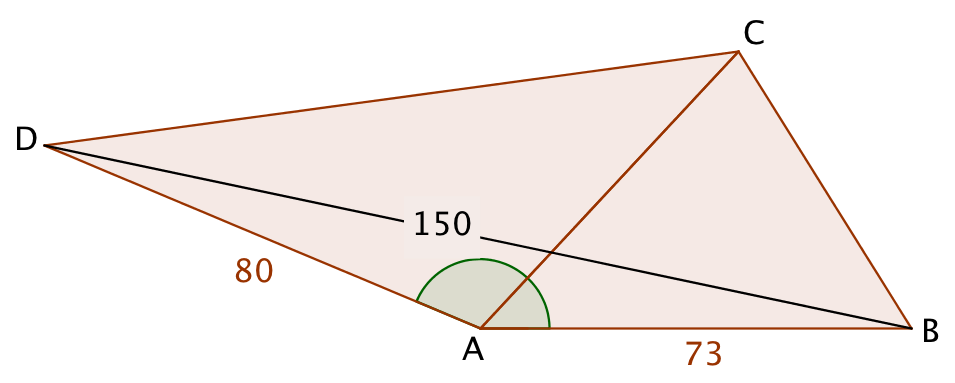
   Vinkel BAD (= x) findes ved hjælp af en cosinusrelation:

   solve(cos(x*1.°)=(80²+73²-150²)/(2*80*73),x)|0<x<180 ▸ x=157.246

   Dvs ∠A i trekant ABD er 157,2°

Svar på opgave 10:

1. N(t) oprettes i Ti-Nspire:

   n(t):=709.8/(1+0.844*exp(−0.828*t)) ▸ Udført

   Nedenfor er N(t) tegnet i Ti-Nspire for t større end 0 (efter år 2007). På tegningen er t erstattet med x.

   

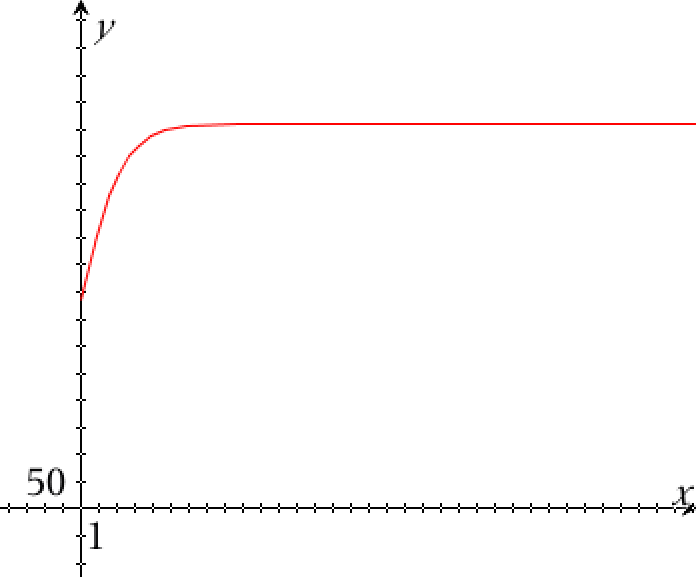
   Antallet af smittede i 2009 beregnes som N(2009-2007) = N(2):

   n(2009-2007) ▸ 611.3

   Dvs antallet af smittede i 2009 er 611

2. Man skal løse ligningen N(t) = 700 med hensyn til t. Dette gøres ved hjælp af solve-kommandoen:

   solve(n(t)=700,t) ▸ t=4.9506

   Dette rundes op til 5 og man får, at 700 smittede passeres i 2007 + 5 = 2012

3. N'(t) beregnes i Ti-Nspire ved hjælp af følgende kommando:

   derivative(n(t),t)|t=3 ▸ 36.1103

   Dvs. N'(3) = 36,1 smittede/år.

   Dette tal er den hastighed som antallet af smittede ændres med efter 3 år.

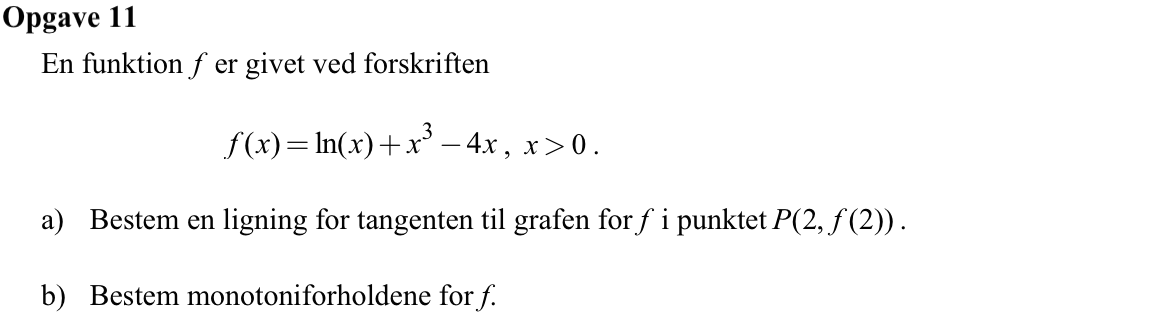
Svar på opgave 11:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=ln(x)+x³-4*x ▸ Udført

   Tangenyten til kurven for f gennem P = (2,f(2)) findes med kommandoen:

   y=tangentLine(f(x),x,2.) ▸ y=8.5*x-16.30685

   Dvs. tangentens ligning er y=8,5·x-16,3

2. Man skal løse ligningerne f´(x) > 0 og f´(x) < 0 for at finde ud af, hvornår funktionen vokser og aftager.

   solve(derivative(f(x),x)>0.,x)|x>0 ▸ 0.<x<0.26376 or x>1.

   solve(derivative(f(x),x)<0.,x)|x>0 ▸ 0.26376<x<1.

   Dvs. f vokser for 0 < x < 0,264, aftager for 0,264 < x < 1 og vokser for x > 1

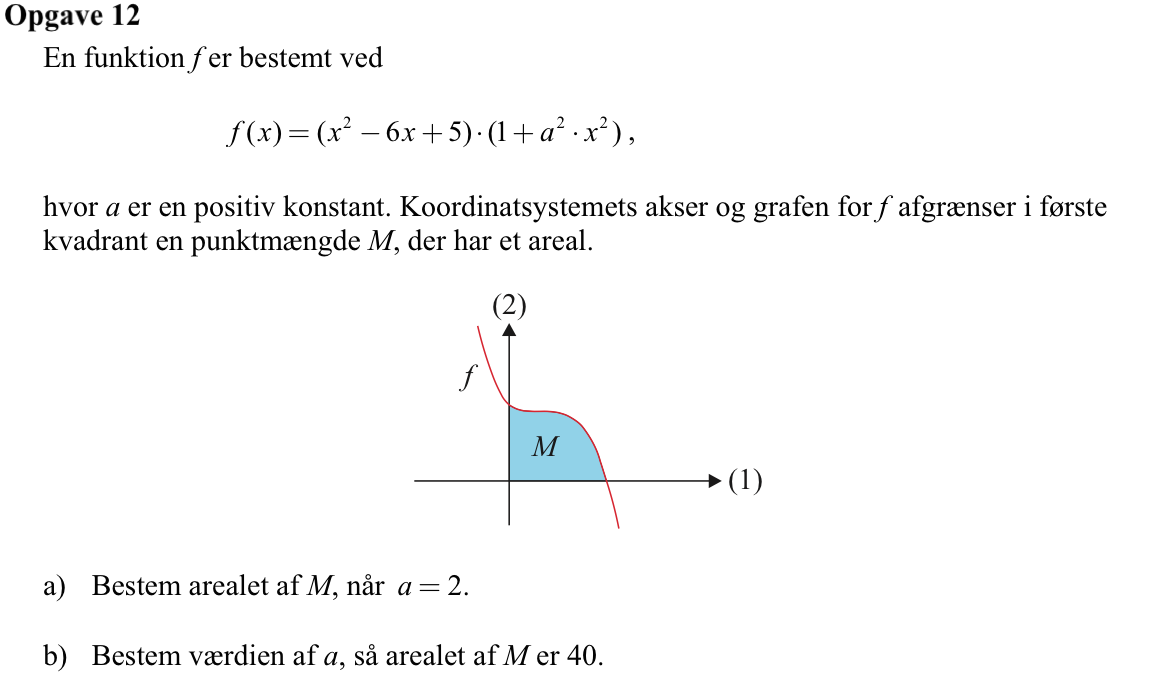
Svar på opgave 12:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=(x²-6*x+5)*(1+a²*x²) ▸ Udført

   Man skal finde nulpunktet (første nulpunkt) for f på x-aksens positive del. Dette gøres med solve kommandoen:

   solve(f(x)=0,x) ▸ x=1 or x=5

   Det mindste nulpunkt er x = 1. Man bestemmer derfor arealet af M som integralet af f(x) fra x = 0 til x = 1, når a = 2. Dette gøres med kommandoen:

   integral(f(x),x,0,1)|a=2. ▸ 3.8

   Dvs arealet af M er 3,8

2. Man beregner a med følgende kommando i Ti-Nspire:

   solve(integral(f(x),x,0,1)=40.,a)|a>0 ▸ a=10.135

   Dvs. det a som giver M et areal på 40 er a = 10,135