Svar på opgave 1:

1. Linjens ligning kan skrives y = ax + b. Koefficienten a er linjens hældning. Den findes ud fra punkternes koordinater ved hjælp af formlen:

   a = (9 - 2)/(-3 - 4) = 7/(-7) = -1. Dermed har man den foreløbige ligning: y = -x + b. Koefficienten b findes ved at indsætte et punkt. Her vælges P = (4,2):

   y = -x + b ⇒ 2 = -4 + b ⇒ 2 + 4 = b ⇒ b = 6.

   Dvs. linjen har ligningen y = -x + 6

Svar på opgave 2:

1. (x + 4)² + (x - 4)² =

   x² + 2·4·x + 4² + x² - 2·4·x + 4² =

   x² + 16 + x² + 16 =

   2x² + 32

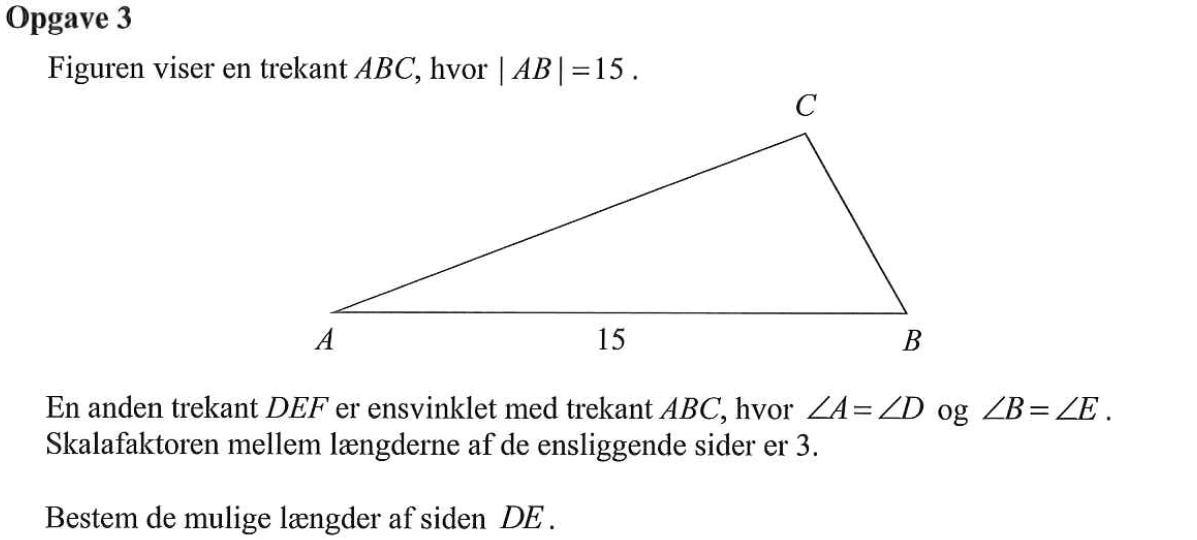
Svar på opgave 3:

1. Skaleringsfaktoren er forholdet mellem to ensliggende sider i hver sin trekant. Med ensliggende menes, at de to sider ligger mellem to lige store vinkler. Siderne AB og DE er således ensliggende, da ∠A = ∠D og ∠B = ∠E.

   Der gælder med andre ord, at enten |AB|/|DE| = 3 eller |DE|/|AB| = 3. Man kan ikke se af opgaven, hvordan skaleringsfaktoren er beregnet.

   Idet man indsætter |AB| = 15 får man følgende to ligninger med hensyn til |DE|:

   15/|DE| = 3 ∨ |DE|/15 = 3 ⇒

   15 = 3·|DE| ∨ |DE| = 3·15 ⇒

   |DE| = 15/3 ∨ |DE| = 45 ⇒

   |DE| = 5 ∨ |DE| = 45

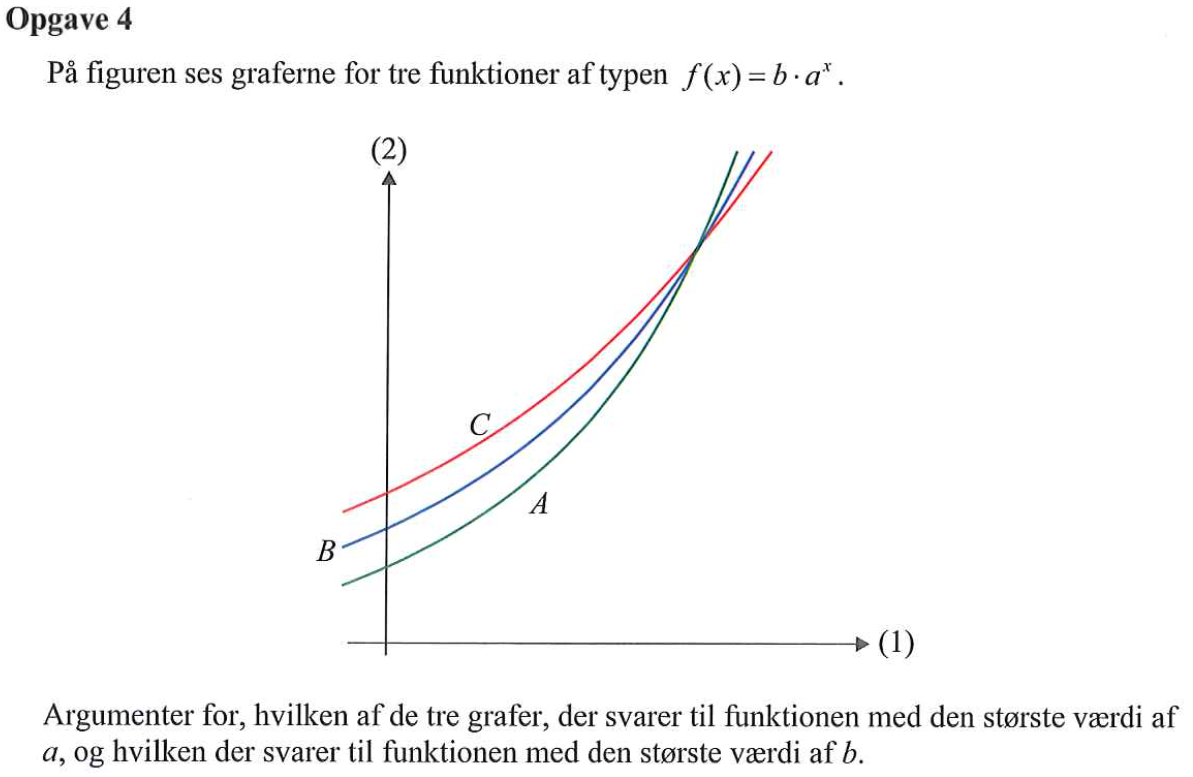
Svar på opgave 4:

1. Koefficienten b viser, hvor højt oppe på y-aksen, at f(x) skærer aksen. Koefficienten a siger hvor hurtigt, at f(x) går mod uendelig.

   Dvs. den funktion, der skærer y-aksen højest oppe har den største b-værdi og den funktion der ligger øverst efter det fælles skæringspunkt mellem A, B og C har den højeste a-værdi.

   Dermed gælder: C er graf for funktionen med den højest b-værdi og A er graf for funktionen med den højeste a-værdi

Svar på opgave 5:

1. f´(x) = 3x² + 5. Grafen er en parabel, som er tegnet nedenunder i Geogebra.

   

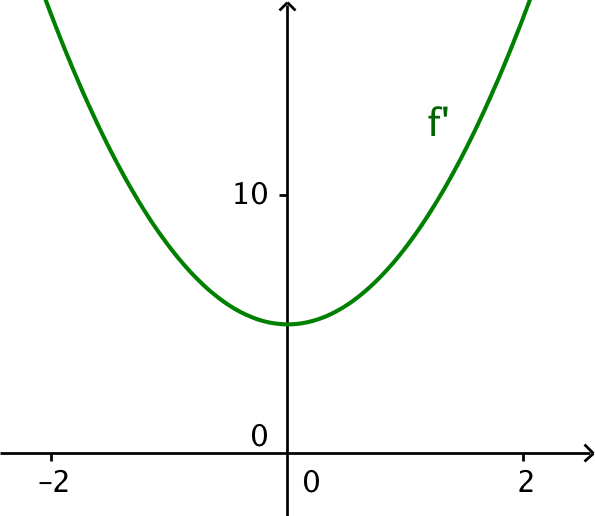
Svar på opgave 6:

1. Integralet bliver:

   

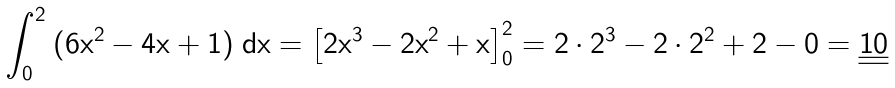
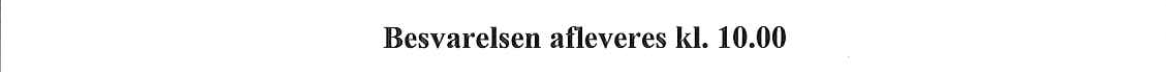
Svar på opgave 7:

1. Man opretter en liste for vægten i Ti-Nspire.

   vægt:={83.,81.5,79.1,78.2,76.,75.5} ▸ {83.,81.5,79.1,78.2,76.,75.5}

   Man opretter dernæst en liste over løbetider:

   løbetid:={6.48,6.42,6.28,6.22,6.2,6.15} ▸ {6.48,6.42,6.28,6.22,6.2,6.15}

   Man laver lineær regression på de to lister ved hjæp af kommandoen Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Lineær regression (mx + b)...

   LinRegMx vægt,løbetid,1: CopyVar stat.RegEqn,f1: stat.results ▸

   

   Af listen fremgår at m = a = 0,0431 og b = 2,889

2. Koefficienten a er det antal minutter, som hun forbedrer sin tid, hver gang hun taber et kilogram (eller omvendt: forværrer sin tid hver gang hun tager et kilogram på).

   Den gennemsnitlige løbetid pr. kilometer ved en vægt på 74 kilogram er lig med f(74). Dette tal findes i Ti-Nspire ved hjælp af f1(x), som er den regressionsfunktion, Ti-Nspire automatisk opretter.

   f1(74) ▸ 6.081

   Dvs. løbetiden er 6,08 min./km

3. Man skal løse ligningen f(x) = 6 med hensyn til x. Dette gøre med solve-kommandoen i Ti-Nspire:

   solve(f1(x)=6,x) ▸ x=72.123

   Dvs. hendes vægt skal i følge modellen være 72,1 kilogram

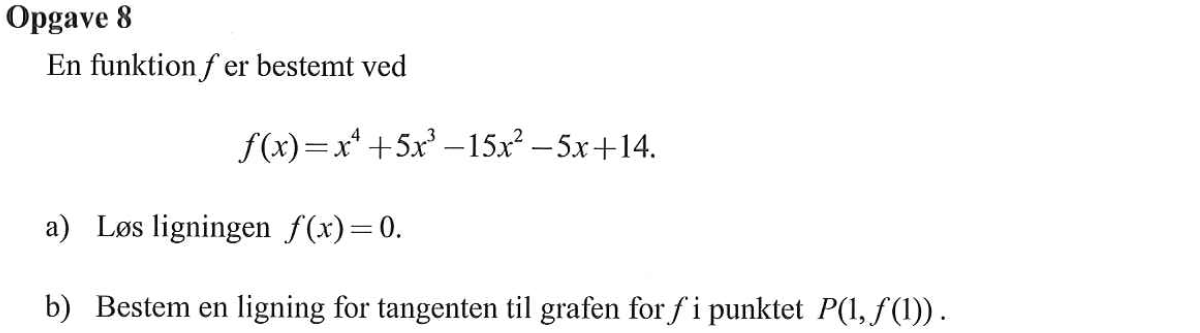
Svar på opgave 8:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=x⁴+5*x³-15*x²-5*x+14 ▸ Udført

   Man løser ligningen i Ti-Nspire:

   solve(f(x)=0,x) ▸ x=−7 or x=−1 or x=1 or x=2

   Dvs. løsningen er x = −7, x = −1, x = 1 eller x = 2,

2. Man finder tangentligningen ved hjælp af teksten "y=" og kommandoen tangentLine() i Ti-Nspire:

   y=tangentLine(f(x),x,1) ▸ y=16-16*x

   Dvs. tangentens ligning gennem punktet (1,f(1)) er y = -16x + 16

Svar på opgave 9:

1. Man opretter en liste over intervalendepunkter for varighed. Man starter med nedre grænse for første interval og fortsætter med øvre grænse for alle intervaller.

   varighed:={0,2,4,6,8,10,12} ▸ {0,2,4,6,8,10,12}

   Man opretter derefter en liste over hyppigheden for de enkelte varigheder.

   hyppighed:={0,889,722,531,358,341,396} ▸ {0,889,722,531,358,341,396}

   Ud fra hyppigheder opretter man en liste af kummulerede frekvenser.

   kummfrekvens:=cumulativeSum(hyppighed/sum(hyppighed))*1. ▸ {0.,0.2746,0.49768,0.66172,0.77232,0.87766,1.}

   Udfra listerne varighed og kummfrekvens laves en sumkurve i Ti-Nspire.

   

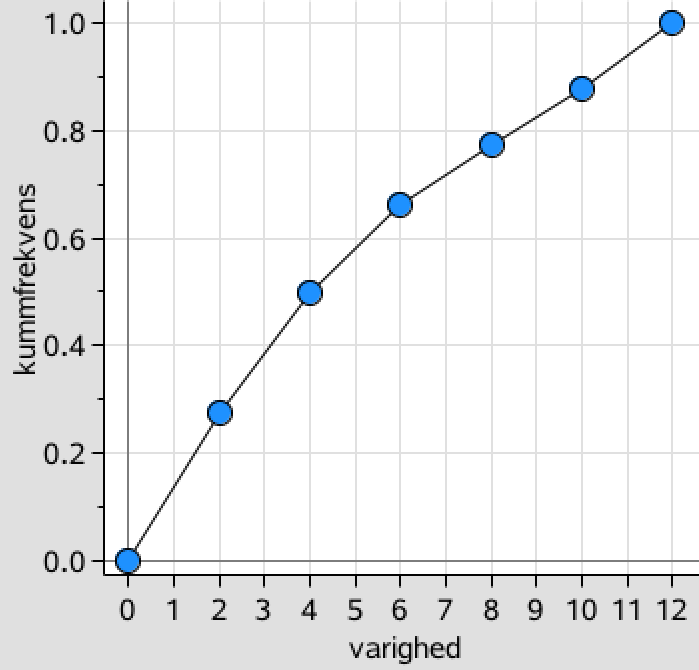
Svar på opgave 10:

1. Man opretter f(x) i Ti-Nspire.

   f(x):=12350*0.96^x ▸ Udført

   Man finder værdien i Ti-Nspire, idet man skal tage funktionsværdien af differencen mellem 2007 og 2012:

   f(2012-2007) ▸ 10069.85

   Dvs. kvadratmeterprisen i 2012 er 10070 kr.

2. Man skal løse ligningen f(x) = 9000 med hensyn til x.

   solve(f(x)=9000,x) ▸ x=7.75

   Man runder op og får, at årstallet er 2007 + 8 = 2015

3. Man opretter g(x) i Ti-Nspire.

   g(x):=14251*0.95^x

   Man skal løse ligningen f(x) = g(x) med hensyn til x.

   solve(f(x)=g(x),x) ▸ x=13.67

   Dvs. årstallet er 2008 + 13 + 0,67·12 mdr. = august 2021

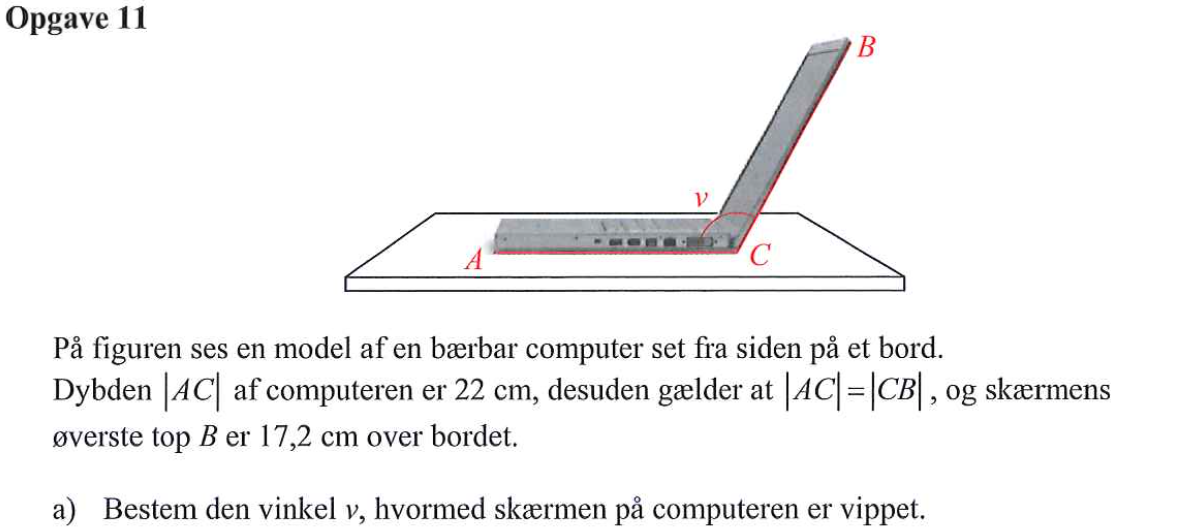
Svar på opgave 11:

1. Der gælder følgende trigonometriske ligning:

   Højden i B = |BC|·sin(v) ⇒ 17,2 = 22·sin(v) ⇒ sin(v) = 0,7818. Det bemærkes af v er stump og at v derfor er 180° - sin^-1(0,7818) ⇒ v = 128,6°

Svar på opgave 12:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=−x²+3.5*x+sqrt(x) ▸ Udført

   Man skal bestemme nulpunkterne for f for at kende grænserne af området M.

   solve(f(x)=0,x) ▸ x=0. or x=4.

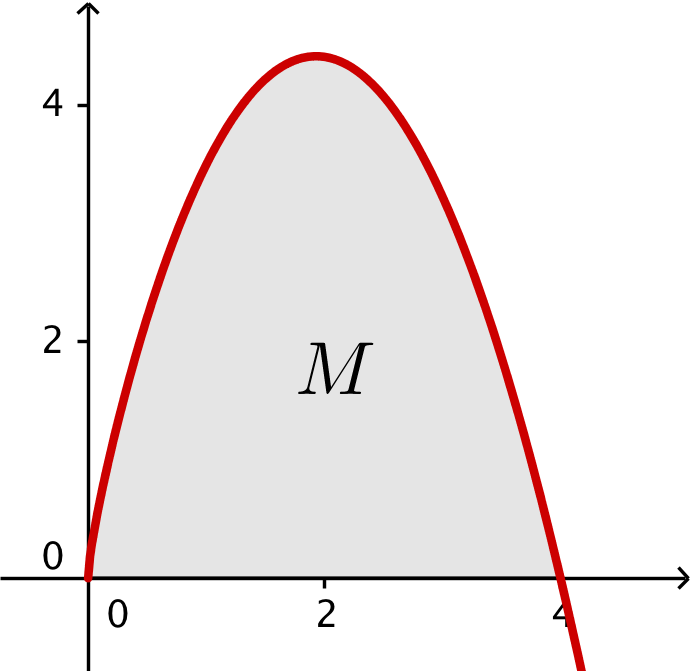
   Man skal beregne arealet af M ved at integrere f(x) fra x = 0 til x = 4.

   integral(f(x),x,0,4) ▸ 12.

   Dvs. arealet af M er 12

   Nedenunder er M tegnet i Geogebra.

   

Svar på opgave 13:

1. Der er tale om en χ² uafhængighedstest med en frihedsgrad.

   Nulhypotesen er, at der ikke er sammenhæng mellen køn (lodret søjle) og farvens betydning (vandret række).

   Man opretter tabellen med observationer som en matrix i Ti-Nspire:

   

   Man bruger kommandoen (Beregninger ▸ Statistik ▸ Statistiske tests ▸ χ²-uafhængighedstest...)

   χ²2way observeret: stat.results ▸

   

   Da PVal er mindre end 0,05 = 5 % forkastes hypotesen

Svar på opgave 14:

1. Man opretter v(t) i Ti-Nspire:

   v(t):=(10-0.1*t²)³ ▸ Udført

   For at bestemme mængden af vand i beholderen efter 5 minutter skal man finde v(5).

   v(5) ▸ 421.875

   Dvs efter 5 minutter er der 422 L i beholderen

   For at finde det tidspunkt, hvor mængden af vand er 4 L skal man løse ligningen: v(t) = 4 med hensyn til t inden for intervallet 0≤t≤10.

   solve(v(t)=4,t)|0<t<10 ▸ t=9.172

   Dvs. der går 9,2 minutter før der er 4 L i beholderen.

2. Man bestemer v'(t) med kommandoen rderivative() i Ti-Nspire.

   derivative(v(t),t) ▸ −0.006*t*(t²-100.)²

   Dvs. V'(t) = −0,006·t·(t² - 100)²

   Man skal finde det tidspunkt, hvor den numeriske værdi af V'(t) er størst.

   fMax(abs(derivative(v(t),t)),t)|0<t<10 ▸ t=4.472

   Dvs. det tidspunkt hvor der løber mest vand ud af beholderne pr. minut er efter 4,47 minutter