Svar på opgave 1:

1. 4x - 7 = 81 ⇒

   4x = 81 + 7 ⇒

   4x = 88 ⇒

   x = 88/4 ⇒

   x = 22

Svar på opgave 2:

1. Konstanten 87 er startværdien, dvs. vægten i kg. ved starten af slankekuren.

   Konstanten -0,45 er hældningskoefficienten eller det antal kg., som personen taber om ugen.

Svar på opgave 3:

1. x² + 3x - 10 = 0 ⇒

   x = -3/2 ±(1/2)√(3² + 4·10) ⇒

   x = -3/2 ±(1/2)√(49) ⇒

   x = -3/2 ±(1/2)·7 ⇒

   x = -3/2 ±7/2 ⇒

   x = -3/2 - 7/2 ∨ x = -3/2 + 7/2 ⇒

   x = -10/2 ∨ x = 4/2 ⇒

   x = -5 ∨ x = 2 ⇒

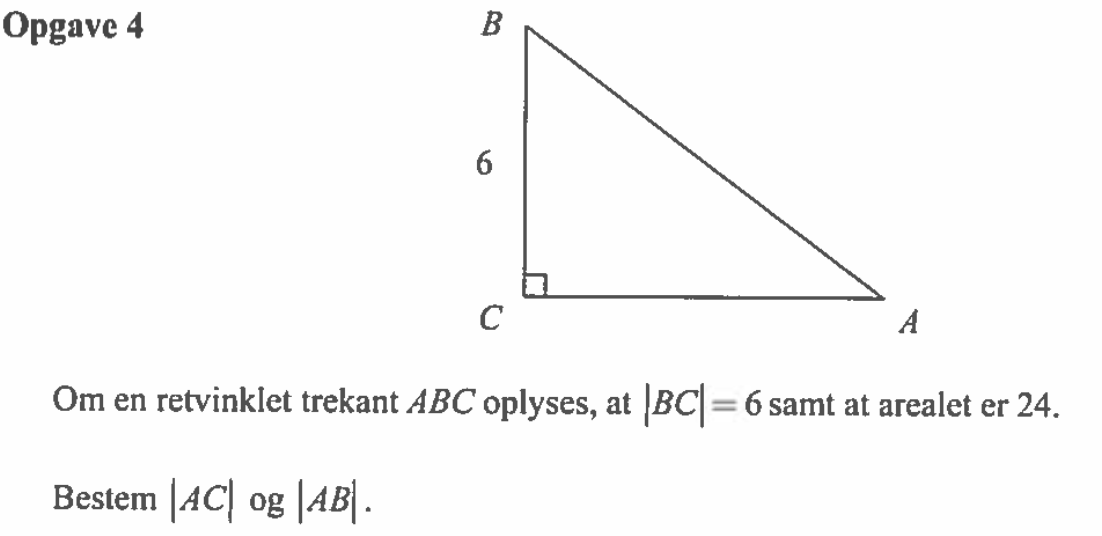
Svar på opgave 4:

1. Der gælder for en retvinklet trekant, at arealet er lig med halvdelen af produktet af kateterne.

   Dvs. Areal = 0,5·|AC|·|BC| ⇒ 24 = 0,5·|AC|·6 ⇒ |AC| = 24/(0,5·6) ⇒ |AC| = 8

   |AB| er hypotenusen i en retvinklet trekant, hvor kateternes længder er 6 og 8. Dvs. |AB| kan findes ved hjælp af Pythagoras læresætning. Man får:

   |AB|² = 6² + 8² ⇒

   |AB|² = 36 + 64 ⇒

   |AB|² = 100 ⇒

   |AB| = √(100) ⇒

   |AB| = 10

Svar på opgave 5:

1. At d er positiv vil sige, at parablen skærer x-aksen i to punkter. A a er positiv betyder, at grenene vender opad. At c er mindre end nul betyder, at parablen skærer y-aksen negative halvdel.

   En mulig parabel er tegnet nedenunder i Geogebra.

   

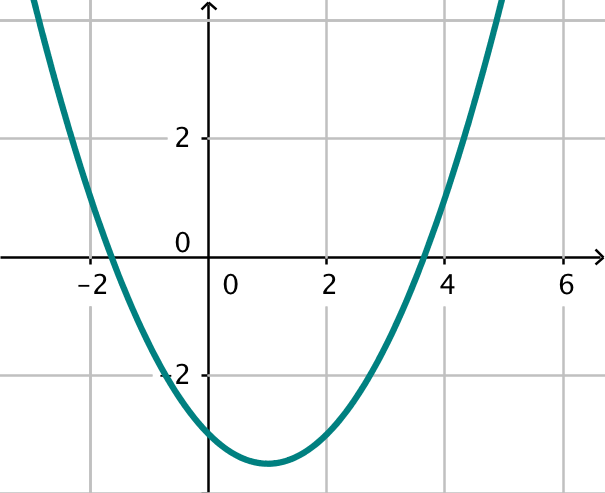
Svar på opgave 6:

1. En vilkårlig stamfunktion til f(x) er F(x) = x⁴ - 3x³ + x + k, hvor k er en reel konstant.

   Man skal finde det k, som gør, at F(1) = 12 ⇒

   1⁴ - 3·1³ + 1 + k = 12 ⇒

   1 - 3 + 1 + k = 12 ⇒

   -1 + k = 12 ⇒

   k = 13

   Dvs. forskriften er F(x) = x⁴ - 3x³ + x + 13

Svar på opgave 7:

1. Man opretter en liste for aldersgrænserne i Ti-Nspire. Første element er nedre grænse i første interval og derefter følger øvre grænse for hvert interval.

   alder:={30,40,50,60,70} ▸ {30,40,50,60,70}

   Man opretter en liste over hyppighederne af hver uddannelse. Man starter listen med et 0 svarende til hyppigheden under nedre grænse for første interval.

   uddannelse:={0,28738,13128,6608,5169} ▸ {0,28738,13128,6608,5169}

   På grundlag af hyppighederne laver man en liste over kummulerede frekvenser.

   kummfrekvens:=cumulativeSum(uddannelse/sum(uddannelse))*1.

   Ud fra listerne alder og kummfrekvens lver man en sumkurve i Ti-Nspire:

   

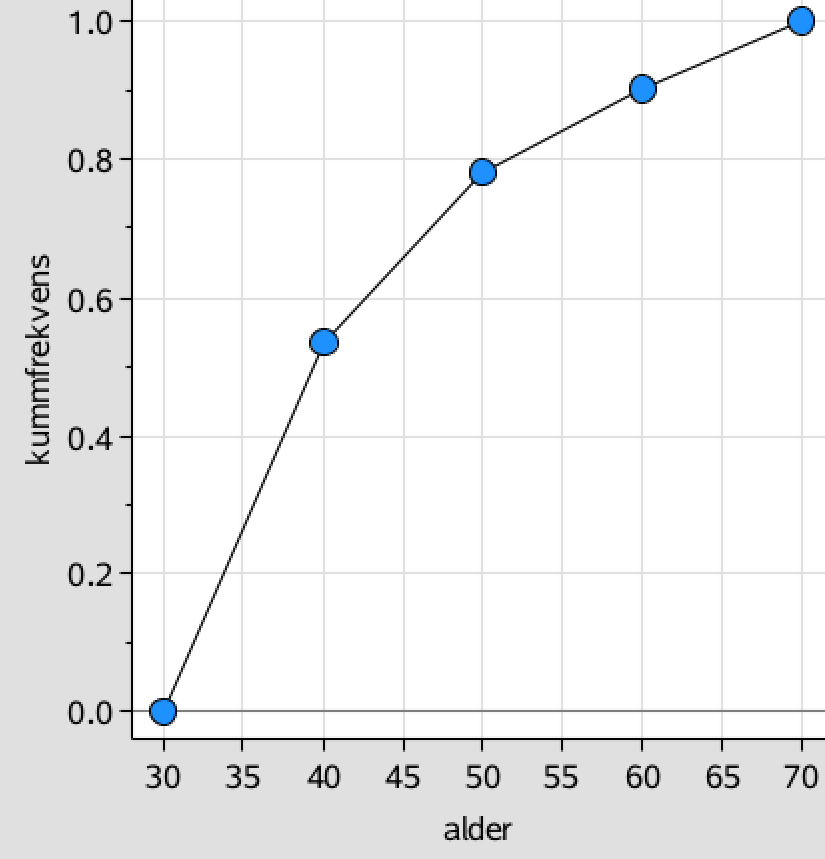
2. Man indtegnet linjerne for frekvenserne 0,25; 0,5 og 0,75 i sumkurven. Førstekoordinaterne mellem disse linjer og sumkurven er kvartilsættet.

   

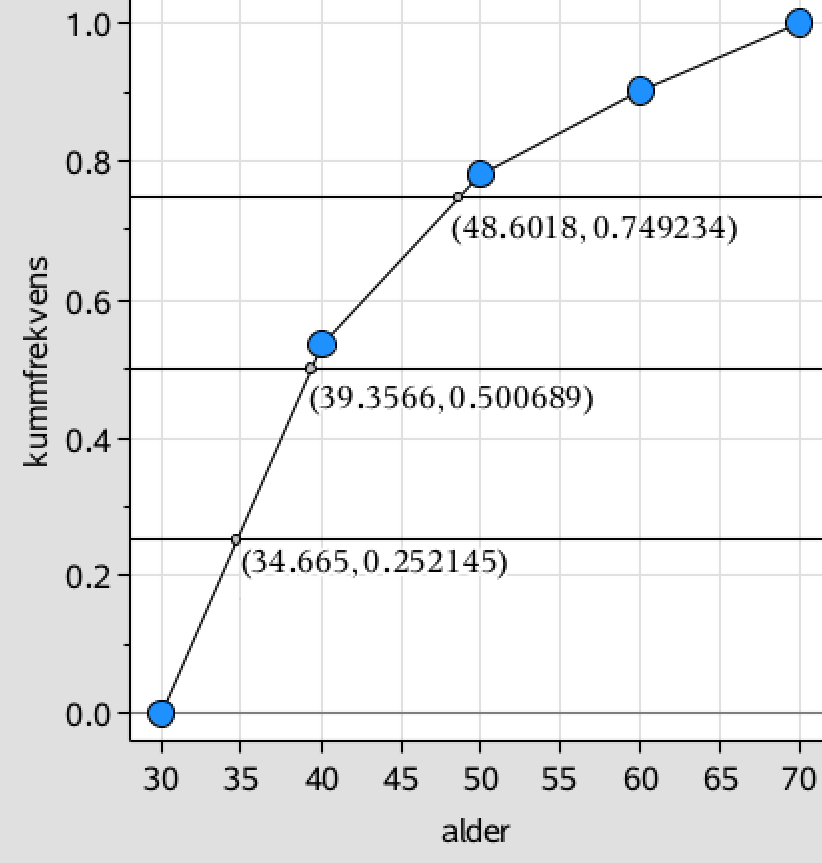
   Man får nedre kvartil = 34,7 år, median = 39,4 år og øvre kvartil = 48,6 år

   Nedenunder er vist hvordan man aflæser sandsynligheden for at en person under 55 år har en videregående uddannelse.

   

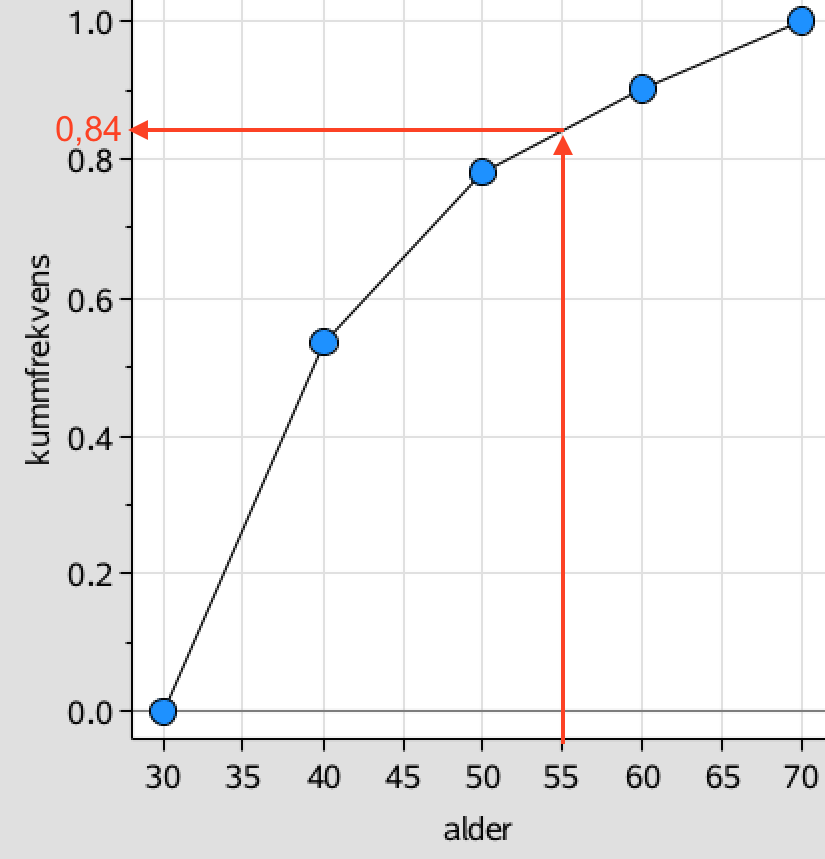
   Denne sandsynlighed ses, at være 0,84. Dermed er sandsynligheden for, at en person over 55 har en videregående uddannelse: 1 - 0,84 = 0,16 = 16 %

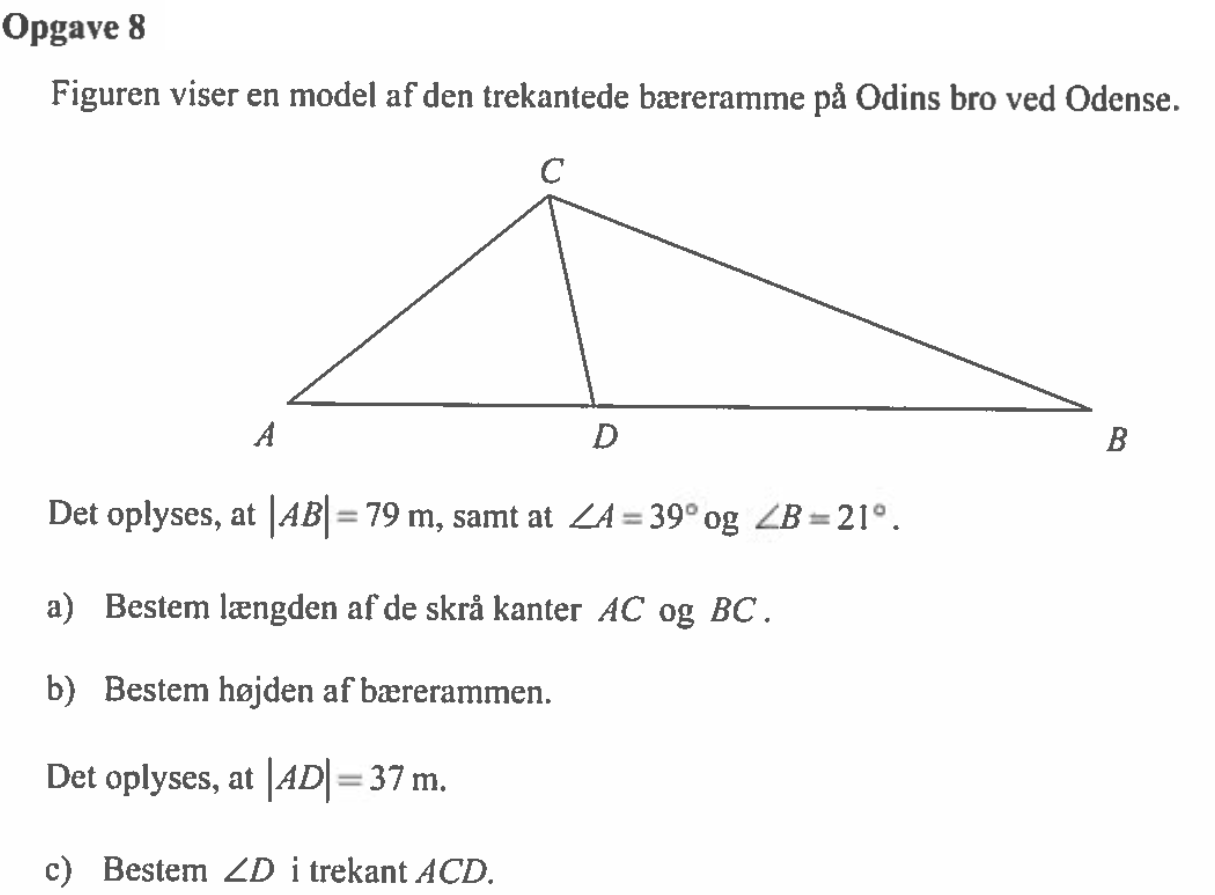
Svar på opgave 8:

1. Man bruger en sinusrelation til af finde |AC| (kaldet x i Ti-Nspire). Det bemærkes at ∠ C = 180° - 39° - 21° = 120°.

   solve(x/(sin(21°)=79/sin(120°),x)*1. ▸ x=32.6908

   Dvs. |AC| = 32,7 m

   |BC| findes ved hjælp af følgende sinusrelation:

   solve(x/sin(39°)=79/sin(120°),x)*1. ▸ x=57.4075

   Dvs. |BC| = 57,4 m

2. Højden af bærerammen findes ved følgende trigonometriske ligning:

   32,691·sin(39°) m = 20,57 m

3. Man finder først |BD| ved hjælp af en cosinusrelation i Ti-Nspire:

   solve(cos(39.°)=(32.691²+37²-x²)/(2*32.691*37),x)|x>0 ▸ x=23.615

   Dernæst indsættes |BD| i en sinusrelation for at finde ∠ADB:

   solve(23.6153/sin(39°)=32.6908/sin(x*1.°),x)|0<x<90 ▸ x=60.595

   Dvs. ∠ADB = 60,6°

Svar på opgave 9:

1. Man opretter en liste over antal år efter 2010 i Ti-Nspire:

   årstal:={2010,2011,2012,2013,2014}-2010 ▸ {0,1,2,3,4}

   Man opretter derefter en liste over antal apparater i mia.:

   antalapp:={1.1,1.3,1.8,2.3,3.2} ▸ {1.1,1.3,1.8,2.3,3.2}

   Man bruger kommandoen for eksponentiel regression på de to lister i Ti-Nspire:

   ExpReg årstal,antalapp,1: CopyVar stat.RegEqn,f1: stat.results ▸

   

   (Kommandoen findes under Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Exponentiel regression...)

   Forskriften er f(x) = 1,0482·1,3108^x

2. a er fremskrivningfaktoren for væksten, dvs. det tal man hvert år skal gange det gamle års tal med for at få det nye.

3. Man opretter g(x) i Ti-Nspire:

   g(x):=0.59*x+6.5 ▸ Udført

   Man skal finde det x der opfylder ligningen f(x) = g(x) for xstørre end 0. Det gøre i Ti-Nspire med solve-kommandoen. Det bemærkes, at Ti-Nspire under regressionen automatisk har oprettet en funktion kaldet f1(x) som er lig med f(x).

   solve(f1(x)=g(x),x)|x>0 ▸ x=8.9378

   De 8,9 år rundes op til 9 og lægges til 2010, så man får, at salget af ikke-smartphones overhaler salget af smartphones i 2019

Svar på opgave 10:

1. Nuhypotesen er at der ikke er nogen sammenhæng mellem det at være hjulbenet og det at spille fodbold.

   Man opretter en matrix med tabellens observerede data i Ti-Nspire:

   

   Man bruger kommandoen Beregninger ▸ Statistik ▸ Statistiske tests ▸ χ² uafhængighedstest... og vælger matricen med observationer

   χ²2way obsfodbold: stat.results ▸

   

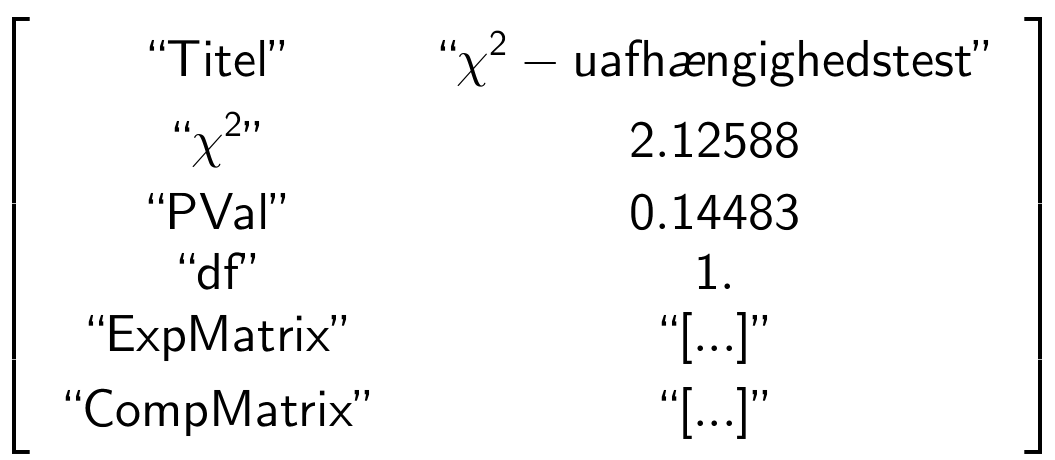
   Da PVal = 0,145 er større end 5 % accepteres nulhypotesen

Svar på opgave 11:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=(x²-15)*exp^−x ▸ Udført

   Ligningen for tangenten gennem (0,f(0)) findes på følgende måde i Ti-Nspire, hvor man kombinener teksten "y=" med kommandoen TangentLine():

   y=tangentLine(f(x),x,0) ▸ y=15*x-15

   Dvs. tangentens ligning er y=15*x-15

2. For at finde monotoniforholdene skal man løse ligningerne f´(x) > 0 og f´(x) < 0

   solve(derivative(f(x),x)>0,x) ▸ −3<x<5

   solve(derivative(f(x),x)<0,x) ▸ x<−3 or x>5

   Heraf ses at f er aftagende for x < -3, voksende for -3 < x < 5 og aftagende for x > 5

Svar på opgave 12:

1. Man opretter O(x) i Ti-Nspire:

   o(x):=x^1.7 ▸ Udført

   Den fakstiske muskelbelastning x, når den oplevede muskelbelastning O(x) er 2 findes i Ti-Nspire med solve-kommandoen:

   solve(o(x)=2,x) ▸ x=1.5034

   Dvs. den faktiske muskelbelastning er 1,5

2. Man skal bruge formlen for procent-procent vækst:

   Procentvækst = (1,5^1,7 - 1)·100 % = 99,2 %

   Man kan også bruge formlen for procent-tilvækst generelt: [(slutværdi - startværdi)/startværdi]·100 %.

   Her er startværdien af x lig med x₀ og slutværdien af x = 1,5·x₀. Man får:

   [(O(1,5·x₀) - O(x₀))/O(x₀)]·100 % = [((1,5·x₀)^1,7 - x₀^1,7)/x₀^1,7]·100 % = [1,5^1,7 - 1]·100 % = 99 %.

Svar på opgave 13:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=(1/25)*x⁴-2*x²+25 ▸ Udført

   Nedenfor er grafen for f tegnet med grønt og området M med brunt i Geogebra:

   

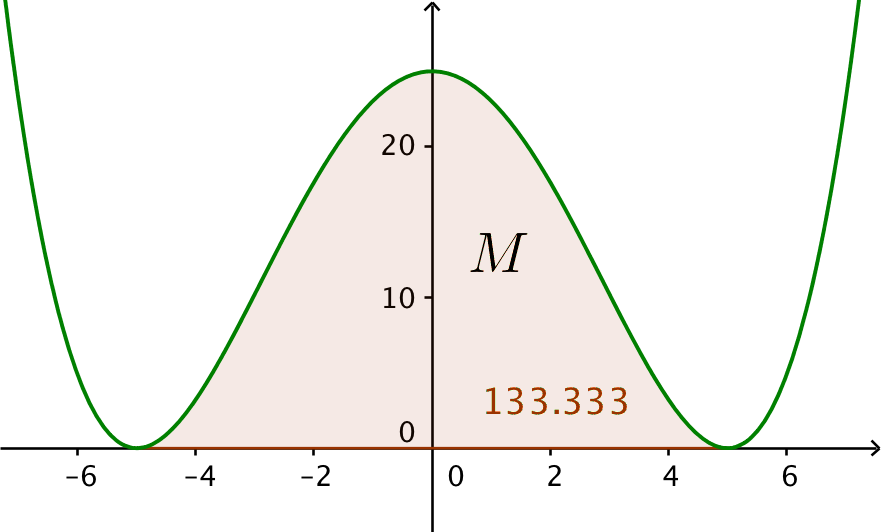
   Arealet under kurven er det bestemte integrale af f(x) mellem f's nulpunkter. Disse nulpunkter findes ved hjælp af solve-kommandoen:

   solve(f(x)=0,x) ▸ x=−5 or x=5

   Arealet er dermed:

   integral(f(x),x,−5,5.) ▸ 133.33

   Arealet af M er 133,3