Svar på opgave 1:

1. 3x + 6 = -2x + 1 ⇔

   3x + 2x = 1 - 6⇔

   5x = -5 ⇔

   x = -1

Svar på opgave 2:

1. En parabel har toppunktet = (-b/2a, c - b²/4), hvor der her gælder at: a = 3, b = -6 og c = 12.

   Toppunkt for parabel: (-(-6)/(2·3), 12 - (-6)²/(4·3)) = (1,9)

Svar på opgave 3:

1. x = antal år efter 2013, f(x) er omsætning i kr. Der er tale om eksponentiel vækst med fremskrivingsfaktoren (1+5%) = 1,05. Startværdien for x = 0 er 25 mio kr.

   Modellen bliver: f(x) = 25 mio.·(1,05)^x

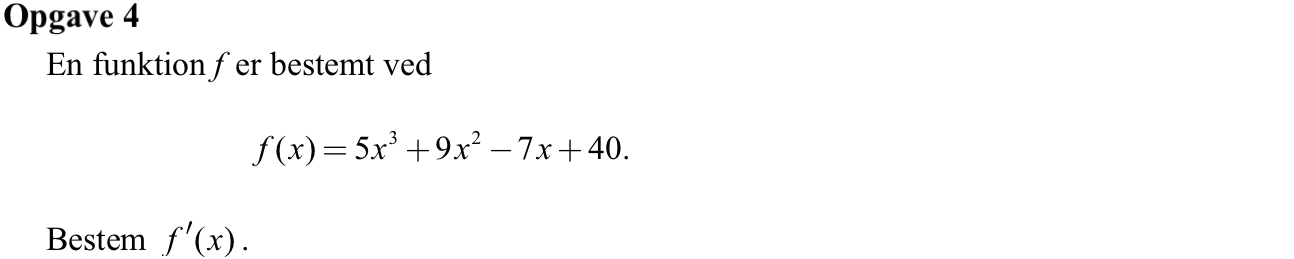
Svar på opgave 4:

1. f'(x) = 5·3·x² + 9·2·x - 7 = 15·x² + 18·x - 7

Svar på opgave 5:

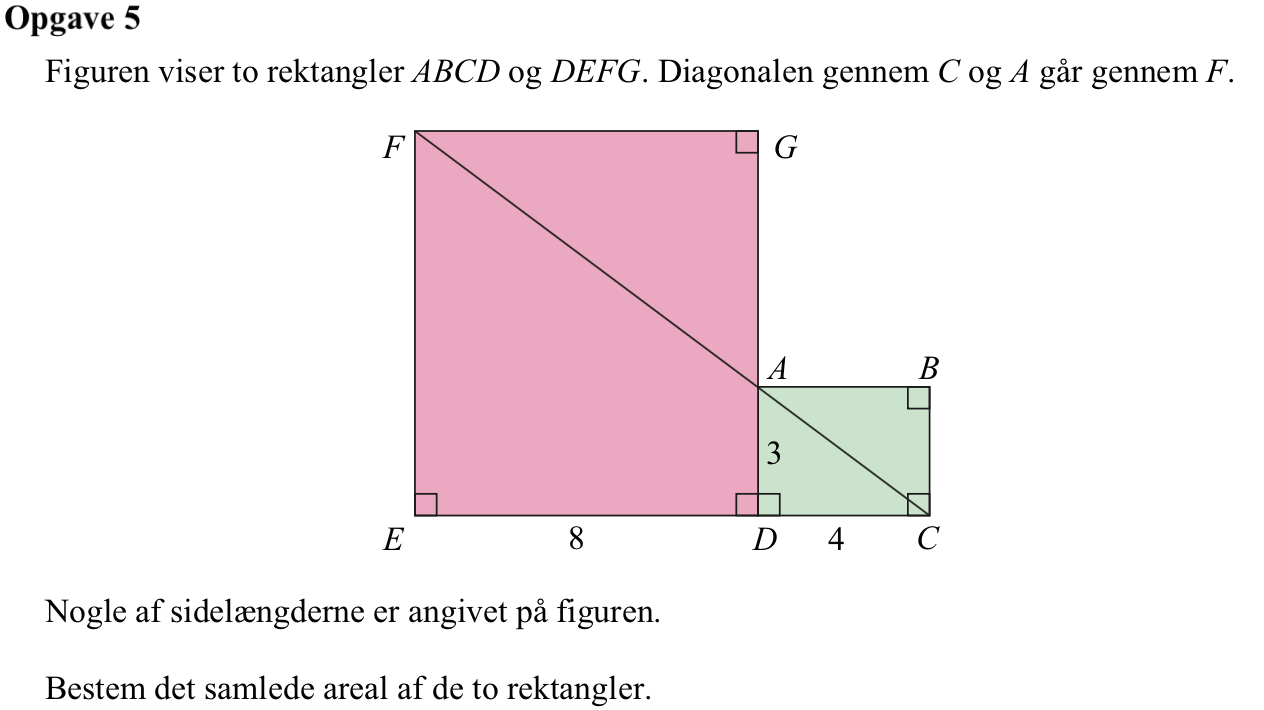
1. Arealet er |EF|·|ED| + |DC|·|DA| = |EF|·8 + 4·3 = |EF|·8 + 12.

   Trekant CEF og trekant CDA er ensvinklede. Der gælder derfor at:

   |EC|/|DC| = |EF|/|DA| ⇒ (|ED| + |DC|)/|DC| = |EF|/|DA| ⇒ (8 + 4)/4 = |EF|/3 ⇒ |EF| = 3·(8 + 4)/4 = 9

   Det samlede areal = 9·8 + 4·3 = 84

Svar på opgave 6:

1. Man ganger ud: 3·(x + 5)·(x + 7) = 3[x² + 12x + 35] = 3x² + 36x + 105.

   Heraf ses at: a = 3, b = 36 og c = 105

Svar på opgave 7:

1. Man indsætter tallene i et regneark i Geogebra og laver tovariabel- lineær-regeressionsanalyse på de nerderste to rækker af tal:

   

   Resultatet er som vist nedenunder, at a = 11,15 og b = 127,9

   

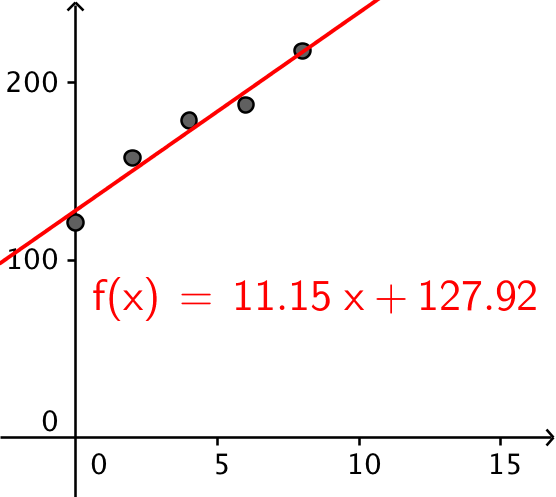
2. Man skal finde f(2007 - 1994) = f(13) = 11,15·13 + 127,9 = 272,9

Svar på opgave 8:

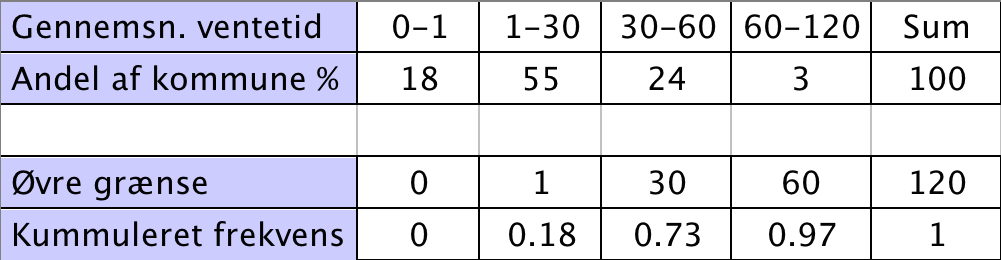
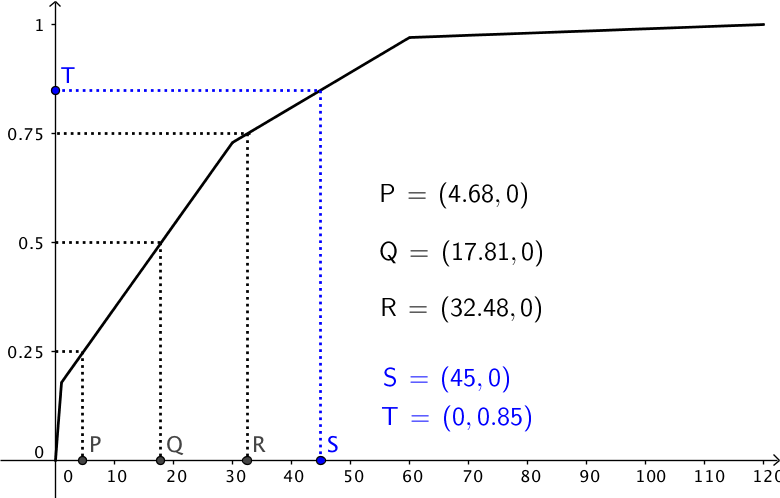
1. Man laver en sumkurve ved at dividere hver andel med 100 og lægge hvert tal til summen af de forrige. For at få kurven til at nå x-aksen indføres punktet (0,0), x = nedre grænse for nederste interval og y = 0.

   

   

2. Af figurens sorte tal fremgår det, at 25%-fraktilen er 4,68, medianen er 17,8 og 75%-fraktilen er 32,5.

   Af figurens blå tal fremgår det, at 0,85 = 85% af alle skal vente 45 dage eller mindre på en plejebolig.

Svar på opgave 9:

1. Man skal bestemme a. Der gælder at halveringstiden = ln(1/2)/ln(a) ⇒

   30,17 = -0,6931/ln(a) ⇒

   ln(a) = -0,6931/30,17 ⇒

   a = exp(-0,6931/30,17) ⇒

   a = 0,9773

2. Man skal finde t, så N(t) = 10 g ⇒

   17,5·(0,9773)^t = 10 ⇒

   (0,9773)^t = 10/17,5 ⇒

   t·ln(0,9773) = ln(10/17,5) ⇒

   t = ln(10/17,5)/ln(0,9773) ⇒

   t = 24,4 år

3. Procentdel = 100%·N(50)/N(0) =

   100%·17,5·0,9773⁵⁰/(17,5·0,9773⁰) =

   100%·0,9773⁵⁰ = 31,7%

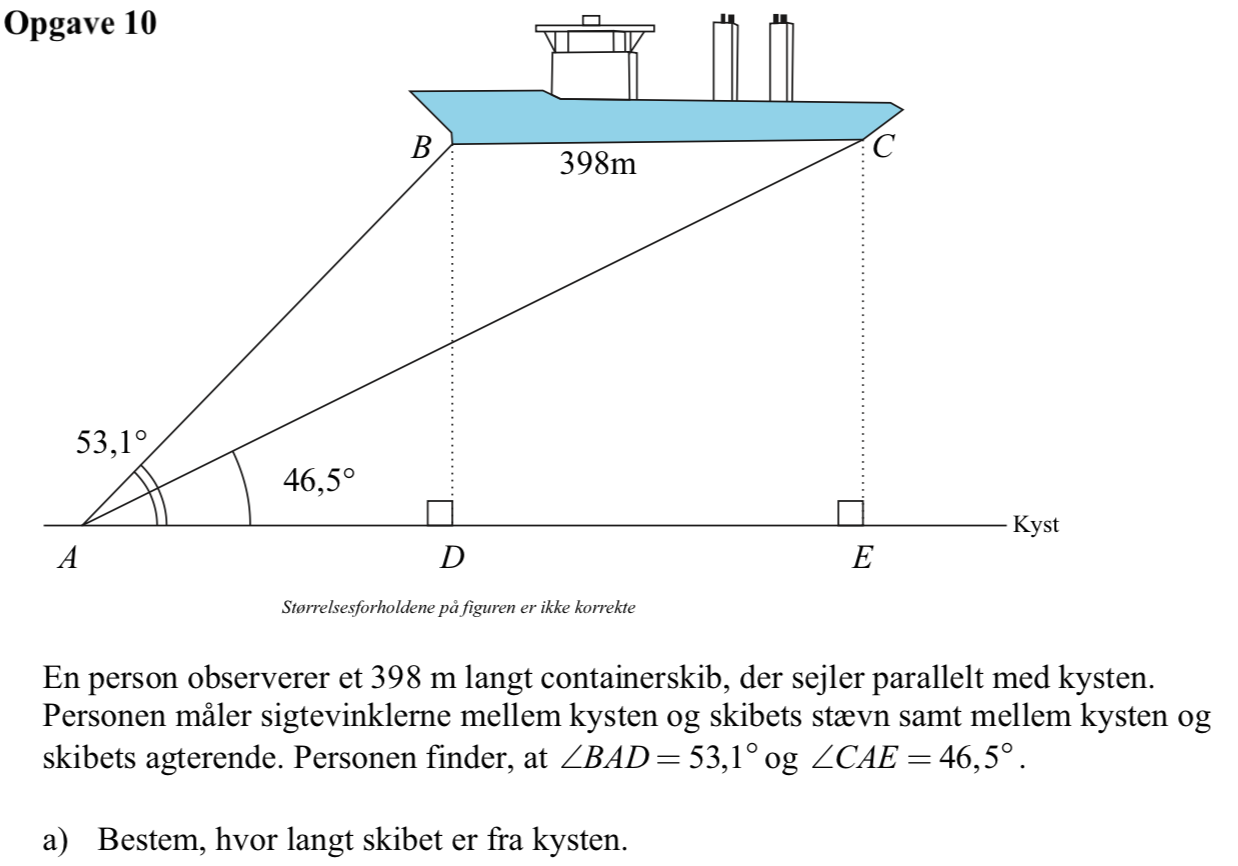
Svar på opgave 10:

1. Afstanden fra kysten til skibet = |BD| = |CE| og kaldes for nemheds skyld x.

   Man har ud fra tegningen:

   

   Man indsætter oplysningen om skibets længde og får resultatet:

   

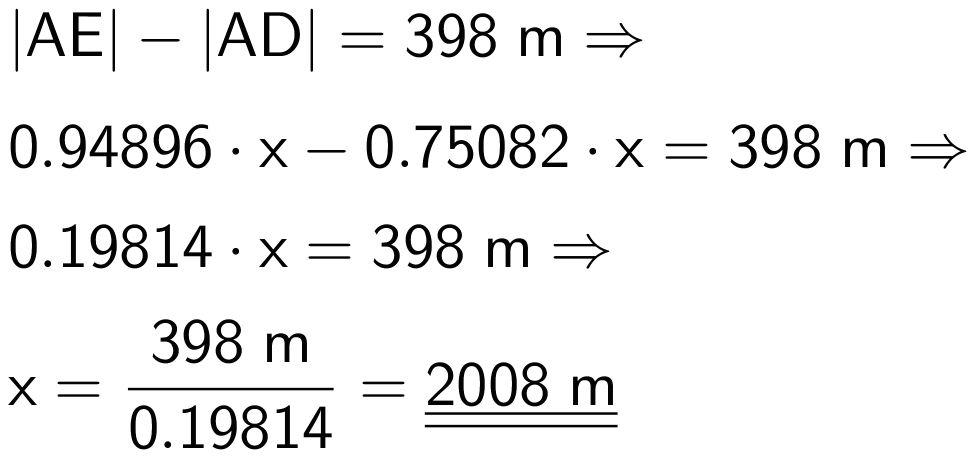
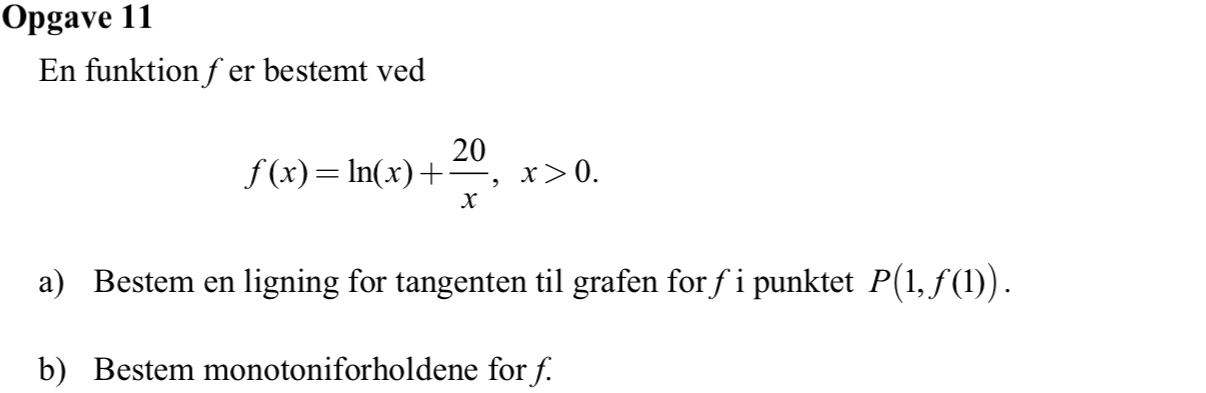
Svar på opgave 11:

1. Man bruger Ti-Nspire kommandoen: y=tangentLine(ln(x)+20/x,x,1) ▸ y=39-19*x

   Dvs. tangentligningen er y = -19x + 39

2. Man skal undersøge fortegn for f´(x). Man bruger Ti-Nspire kommandoerne:

   solve(derivative(ln(x)+20./x,x)>0,x)|x>0 ▸ x>20 og

   solve(derivative(ln(x)+20./x,x)<0,x)|x>0 ▸ 0<x<20

   Første linje viser, at f´(x) > 0 for x > 20, og at f´(x) < 0 for 1 ≶ x < 20. Dvs. monotoniforholdene er:

   f(x) aftager for 0 < x < 20 og vokser for x > 20. X = 20 er et minimum.

Svar på opgave 12:

1. Ligningen f(x) = g(x) løses i Ti-Nspire med kommandoen:

   solve(−x + 8 = −x^2 + 6*x + 2,x) → x = 1 or x = 6

   Skitse i Geogebra:

   

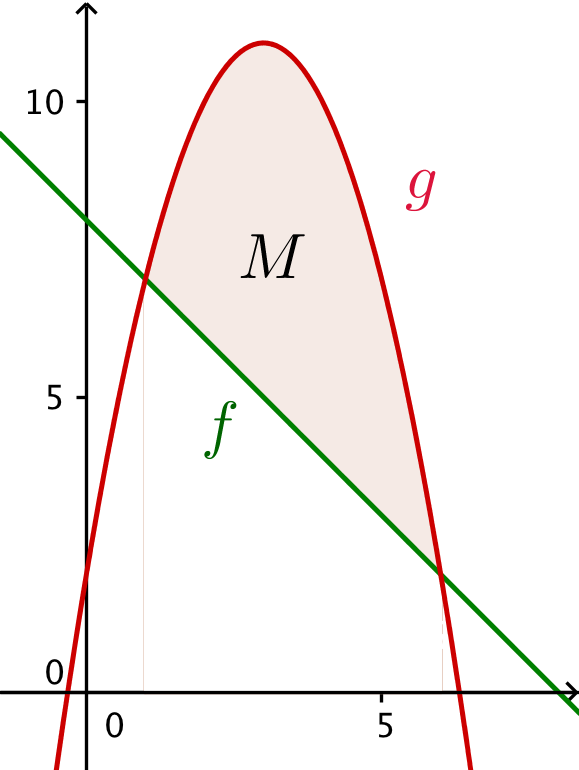
2. Arealet af M findes som integralet af g(x) - f(x) mellem skæringspunkterne x = 1 og x = 6. Arealet beregnes med Ti-Nspire kommandoen:

   

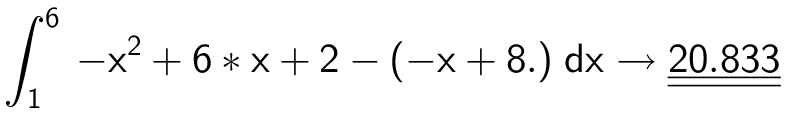
Svar på opgave 13:

1. Længde af hegn: (x - 1) + y + x = 2x + y - 1

   Areal af udendørsområde: x·y - 1·1,2 = x·y - 1,2

2. Man har for hegnets længde: 2x + y - 1 = 10 ⇒ y = 10 + 1 - 2x = 11 - 2x

   Dette udtryk for y indsættes i formlen for undendørsarealet, som kaldes A(x):

   A(x) = x·(11 - 2x) - 1,2 = -2x² + 11x - 1,2.

   Man skal finde nulpunkter lave fortegnsundersøgelse for A'(x).

   A´(x) = -4x + 11. Man får nulpunktet: A´(x) = -4x + 11 = 0 ⇒ x = 11/4 = 2,75. Fortegn for A'(x): A(x) er en parabel der vender grenene nedad, dermed er x = 2,75 et maksimumspunkt.

   Dermed er x = 2,75 m den værdi der giver det største udendørsareal med den givne længde af hegnet.