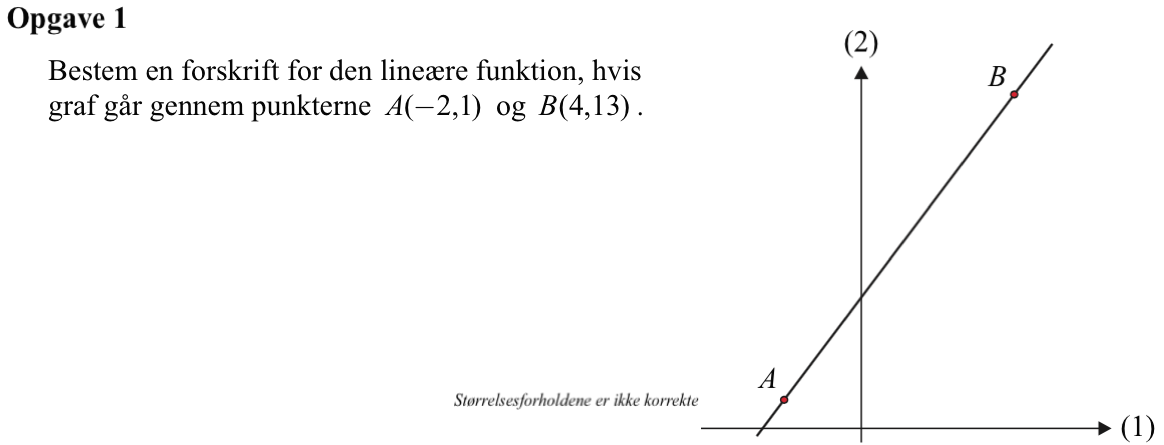
Svar på opgave 1:

1. En lineær funktion kan skrives: f(x) = a·x + b, hvor a og b er konstanter. Man finder a som hældningen af kurven mellem A og B:

   a = (13-1)/(4-(-2)) = 12/6 = 2. Til sidst finder man b ved at indsætte A i f(x) = 2x + b:

   f(-2) = 1 = 2·(-2) + b ⇒ b = 1 + 4 = 5. Dette giver det færdige udtryk:

   f(x) = 2x - 3

   (Som prøve kan man indsætte B: venstre side af udtrykket giver: f(4) = 13, højre side giver: 2·4 + 5 = 13, det vil sige prøven stemmer.)

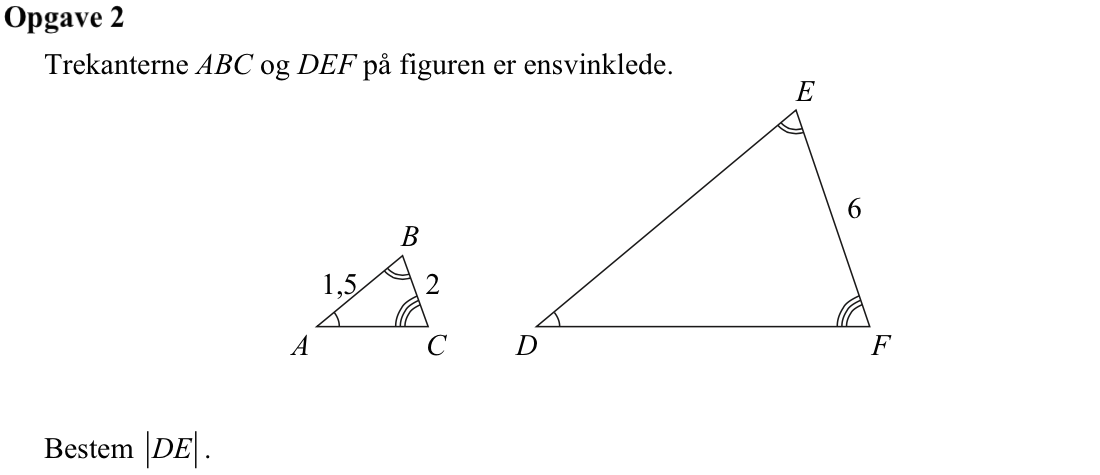
Svar på opgave 2:

1. Skaleringsfaktoren mellem de to trekanter er |EF|/|BC| = 6/2 = 3.

   Dette giver, at |DE| = 3·|AB| = 3·1,5 = 4,5

Svar på opgave 3:

1. f(x) = 2x³ + 4x + 7.

   f´(x) = 6x² + 4

   Dette giver, at f´(1) = 6·1² + 4 = 10

Svar på opgave 4:

1. x koordianten for toppunktet af parablen findes ved at løse ligningen f´(x) = 0 med hensyn til x. Dette giver ligningen:

   f´(x) = 0 ⇒ 8x - 8 = 0 ⇒ x = 1

   y-koordianten findes ved at indsætte x = 1 i f(x). Dette giver f(1) = 4·1² -8·1 + 2 = 2.

   Man har defor, at toppunktet for parablen er (1,-2)

Svar på opgave 5:

1. Når x og y er omvendt proportionale gælder at x·y = k, hvor k er en konstant. Her ses af første lodrette søjle, at k = 10·4 = 40.

   Det vil sige at 20·y = 40 ⇒ y = 2 i anden søjle.

Svar på opgave 6:

1. En stamfunktion til f(x) kan skrives F(x) = ∫f(x)dx

   Dette giver at F(x) = _∫f(x) dx = _∫(6x²-8x) dx = 2x³ - 4x² + k.

   Man skal finde k, så F(2) = 13. Man får:

   F(2) = 13 ⇒ 2·2³ - 4·2² + k = 13 ⇒ k = 13 - 16 + 16 ⇒ k = 13.

   Den søgte stamfunktion bliver: F(x) = 2x³ - 4x² + 13

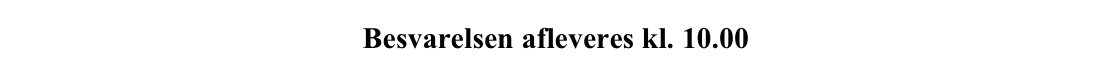
Svar på opgave 7:

1. Man opretter en liste årefter med år efter 2006 i Ti-Nspire:

   årefter:={2006,2007,2008,2009,2010,2011,2012}-2006 ▸ {0,1,2,3,4,5,6}

   Man opretter en anden liste procentdel med procentdele:

   procentdel:={36.5,37.8,39.,40.7,41.1,42.2,43.2} ▸ {36.5,37.8,39.,40.7,41.1,42.2,43.2}

   På disse lister bruger man kommandoen for lineær regression:

   LinRegMx årefter,procentdel,1: CopyVar stat.RegEqn,f1: stat.results ▸

   

   (Kommandoen findes under menuen statistik ▸ statistiske beregninger ▸ Lineær regression (mx+b)...)

   Af dette resultat fremgår det, at a = 1,107 og b = 36,75

2. Man skal bestemme f(2015 - 2006) = f(9). Man får procentdelen: 1,107·9 + 36,75 = 46,7

   Man skal dernæst løse ligningen: f(x) = 50 med hensyn til x. Man får i Ti-Nspire:

   solve(f1(x)=50,x) ▸ x=11.9677

   (Bemærk: f1(x) er det automatiske navn for løsningsfunktionen i 7a). Man kan også selv definere en funktion f(x):=1.107*x+36.75) og regne på den.

   Resultatet rundes op til 12 og lægges til 2006, så man får, at 50 % passeres i år 2018

   (Er man i tvivl om hvorvidt, man skal runde op eller ned, kan man regne f(x) ud for x = 11 og x = 12 og se, hvilken værdi, der giver en værdi højere end 50.)

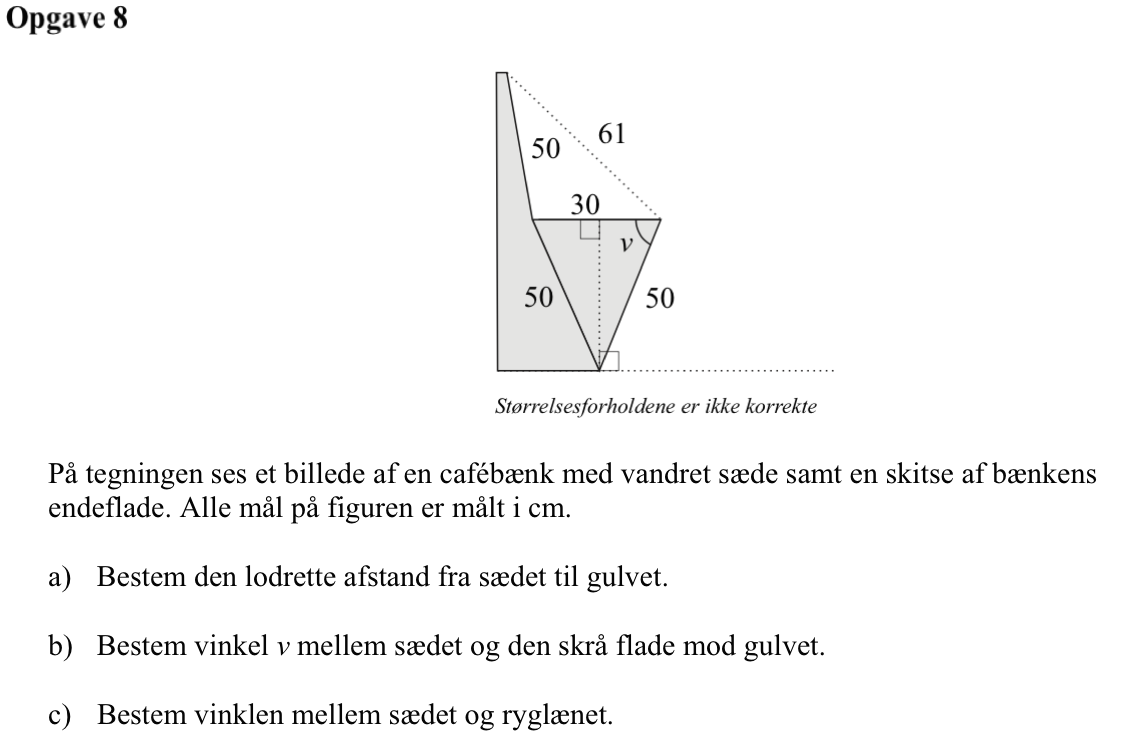
Svar på opgave 8:

1. Kald afstanden mellem sæde og gulv for h. Af tegningen nedenunder fremgår det, at h er katete i en retvinklet trekant, hvor hypotenusen er 50 og den anden katete er 15. (Det sidste ses af, at h også er højden i en ligebenet trekant, hvor førnævnte katete indgår som halvdelen af grundlinjen.)

   

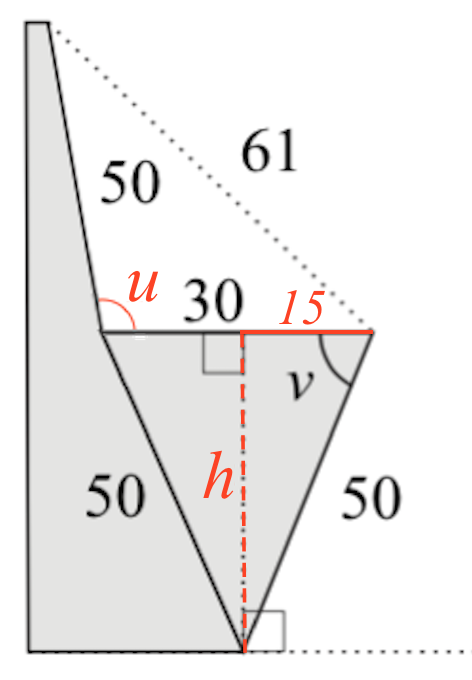
   Man finder h ved hjælp af Pythagoras læresætning: h = √(50² - 15²) cm = 47,7 cm

2. Der gælder at (50 cm)·cos(v) = 15 cm. Dvs. v = cos^-1(15/50) ⇒ v = 72,5°

3. Vinklen, der er kaldet u på ovenstående tegning, kan findes ved hjælp af cosinusrelationen. I Ti-Nspire gøres det ved hjælp af følgende kommando, hvor det forudsættes, at u ligger mellem 0 og 180°:

   solve(cos(u*1.°)=(50² + 30² - 61²)/(2*30*50))|0<u<180 ▸ u=96.14

   (Bemærk: udtrykket u*1.° sikrer, at resultatet bliver i grader, men man skal ikke skrive gradtegn i betingelsen |0<u<180.)

   Dermed er vinklen mellem sædet og ryglænet: 96,1°

Svar på opgave 9:

1. Man skal beregne f(2015 - 1950) = f(65) = 2586·1,017⁶⁵ = 7735,5 mio mennesker, som er verdens befolkning i 2015 i følge modellen.

2. 2586 mio. er startværdien, dvs. antallet af mennekser i verden år 1950. 1,017 er fremskrivningsfaktoren, dvs. det tal som verdens befolknings skal ganges med hvert år for at få tallet for det nye år.

Svar på opgave 10:

1. Grafen er tegnet i Geogebra og vist nedenunder (x er anvendt i stedet for t for grafen):

   

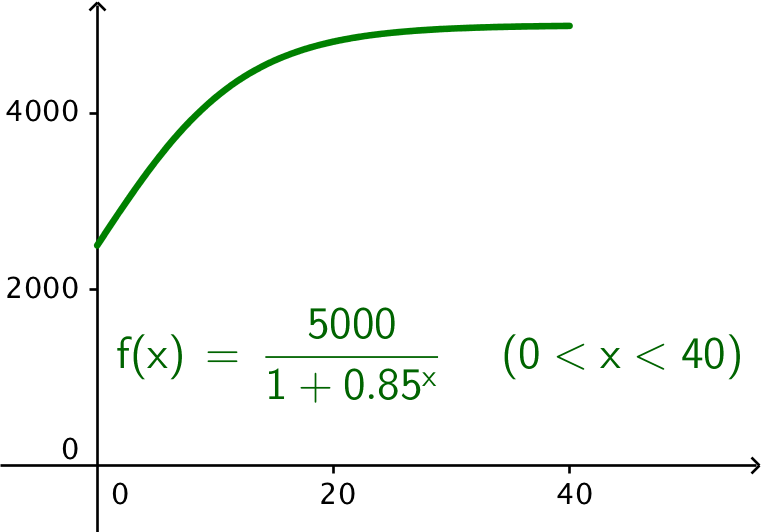
   Man skal løse ligningen n(t) = 4000 (for 0 ≤ t ≤ 40). Det gøres i Ti-Nspire:

   n(t):=5000/(1+0.85^t) ▸ Udført

   solve(n(t)=4000,t)|0≤t≤40 ▸ t=8.5300

   Det vil sige, at man når op på 4000 individer efter 8,5 uger

2. Man finder N'(10) i Ti-Nspire:

   derivative(n(x),x)|x=10 ▸ 111.678

   N'(t) = 111,6 viser vækstraten i antal individer pr uge efter 10 uger.

Svar på opgave 11:

1. Arealet af M er integralet af f(x) fra x=0 til x=2. Dette findes i Ti-Nspire:

   integral(0.25*x³-0.75*x²+2,x,0,2) ▸ 3.

   Det vil sige at arealet af M er 3

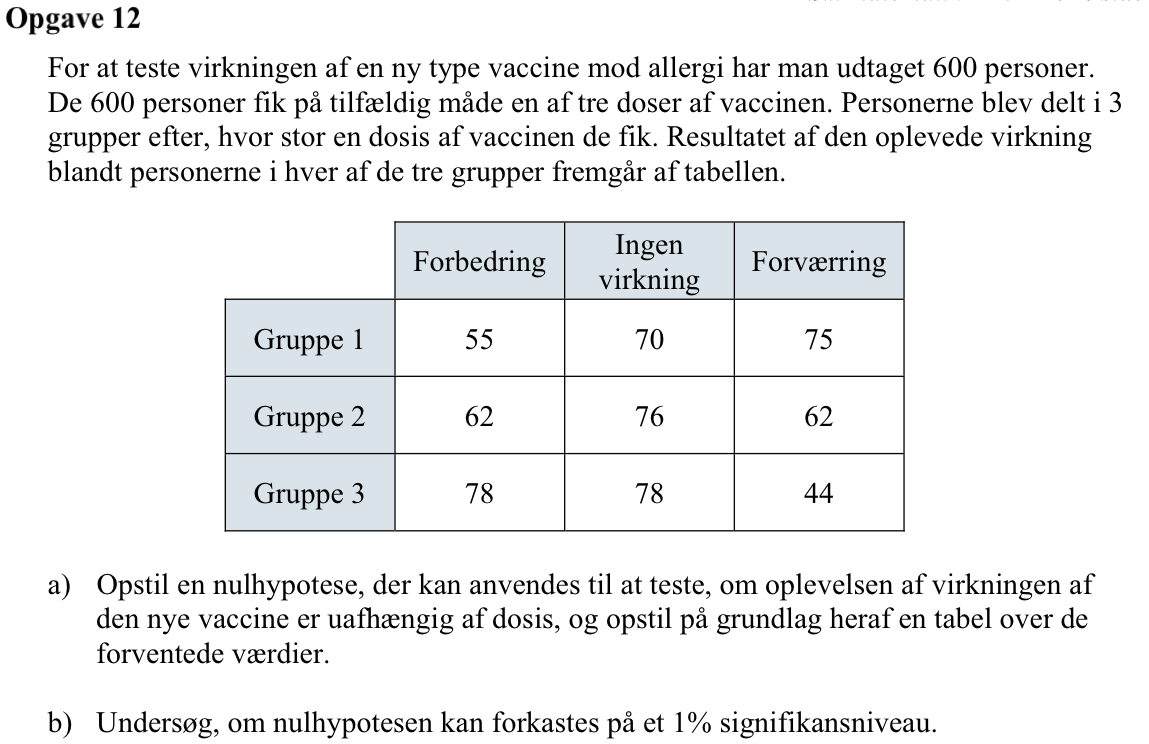
Svar på opgave 12:

1. Nulhypotesen er, at vaccinens virkning, som ses henad i skemaet, er uafhæng af forsøgsgruppen, som ses nedad.

   Man opretter en 3×3 matrix i Ti-Nspire emd tallene:

   

2. Man laver en uafhængighedstest på matrixen med kommandoen:

   χ²2way dosis_test: stat.results ▸

   

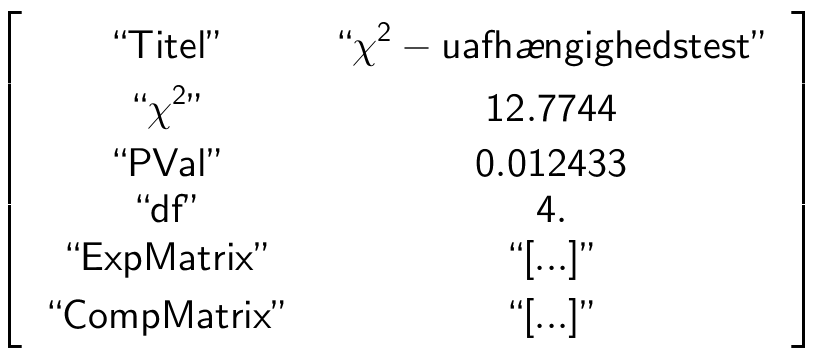
   (Kommandoen findes under menuen statistik ▸ statistiske tests ▸ χ²-uafhængighedstest...)

   Det ses, at PVal = 0,0124 = 1,24 %. Da dette er større end 1 % accepteres nul-hypotesen.

Svar på opgave 13:

1. Man løser ligningen f(x) = 0 i Ti-Nspire:

   f(x):=x³-2*x²-11*x+12 ▸ Udført

   solve(f(x)=0,x) ▸ x=−3 or x=1 or x=4

   Det vil sige, f(x) = 0 for x= −3 ∨ x=1 ∨ x=4

2. Man skal løse ligningen f´(x) = 9 for x. Dette giver i Ti-Nspire:

   solve(derivative(f(x),x)=9.,x) ▸ x=−2. or x=3.333

   Det vil sige, at første koordinaterne er x = -2 ∨ x = 3,333