Svar på opgave 1:

1. Modellen bliver

   f(x) = 120·1,07^x

   hvor f(x) er antal mio. alger pr. L og x er antal timer efter målingen af begyndelses­koncentrationen har fundet sted.

Svar på opgave 2:

1. Man får:

   (a + b)² - a² - ab =

   a² + 2ab + b² - a² - ab =

   ab + b²

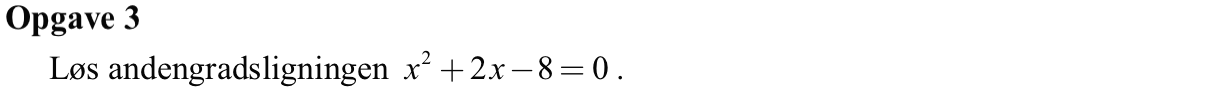
Svar på opgave 3:

1. x² + 2x - 8 = 0 ⇔

   x = {-2 ± √[4 - 4·1·(-8)]}/2 ⇔

   x = {-2 ± √[36]}/2 ⇔

   x = {-2 ± 6}/2 ⇔

   x = -1 ± 3 ⇔

   x = -4 ∨ x = 2

Svar på opgave 4:

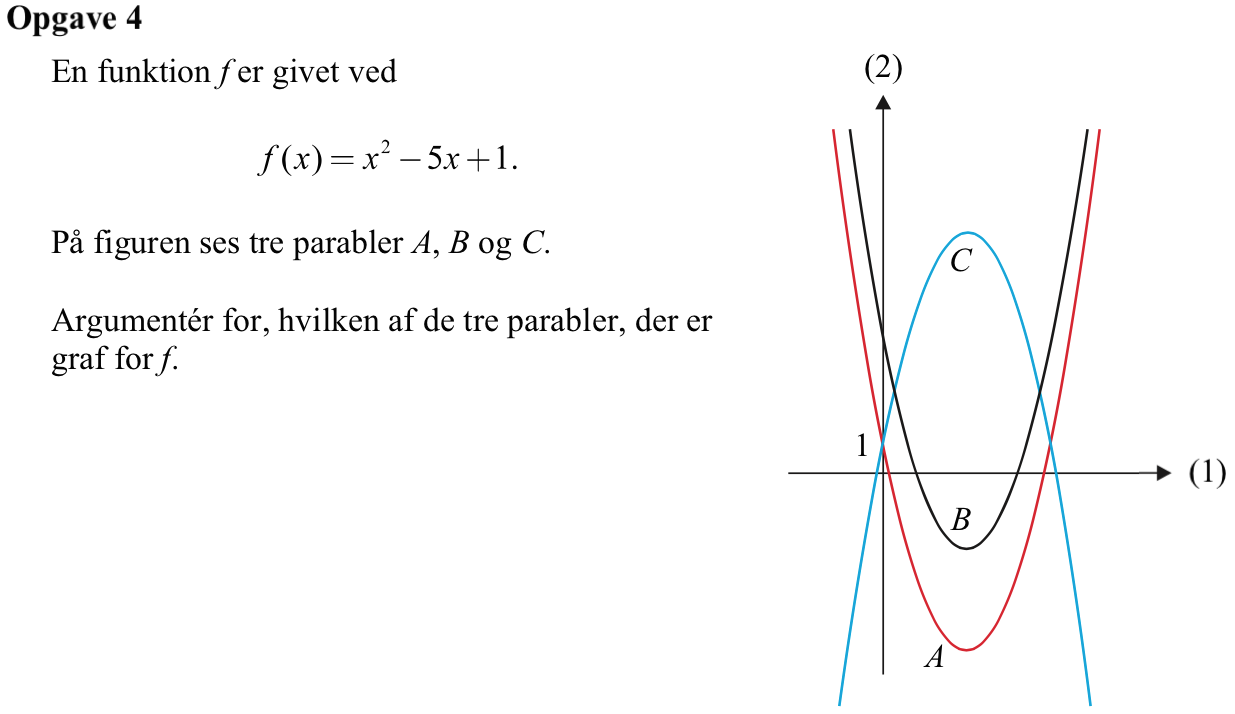
1. f(x) kan skrives: ax² + bx + c. Det er en parabel, hvor a = 1, b = -5 og c = 1. Man får:

   a > 0: parablen vender grenene opad,

   b < 0: parablens hældning for x = 0 er negativ og

   c = 1: parablen skærer y-aksen for y = 1.

   Det svarer til kurve A

Svar på opgave 5:

1. Man har: 0,5·|AC|·6 = 24 ⇒ |AC| = 24/(0,5·6) = 8

   |AB|² = 6² + 8² ⇒

   |AB|² = 100 ⇒

   |AB| = 10

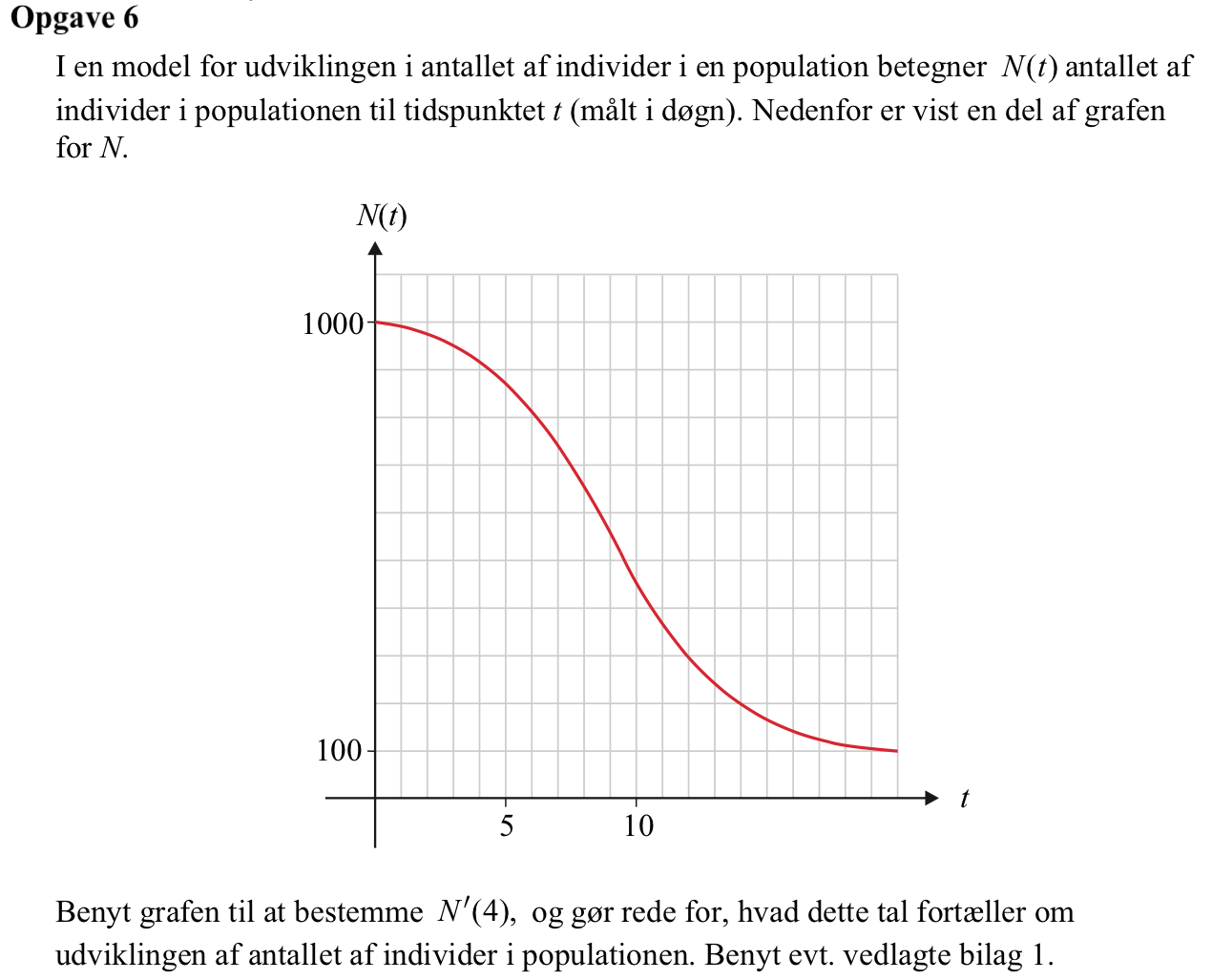
Svar på opgave 6:

1. Man tegner tangenten for x = 4:

   

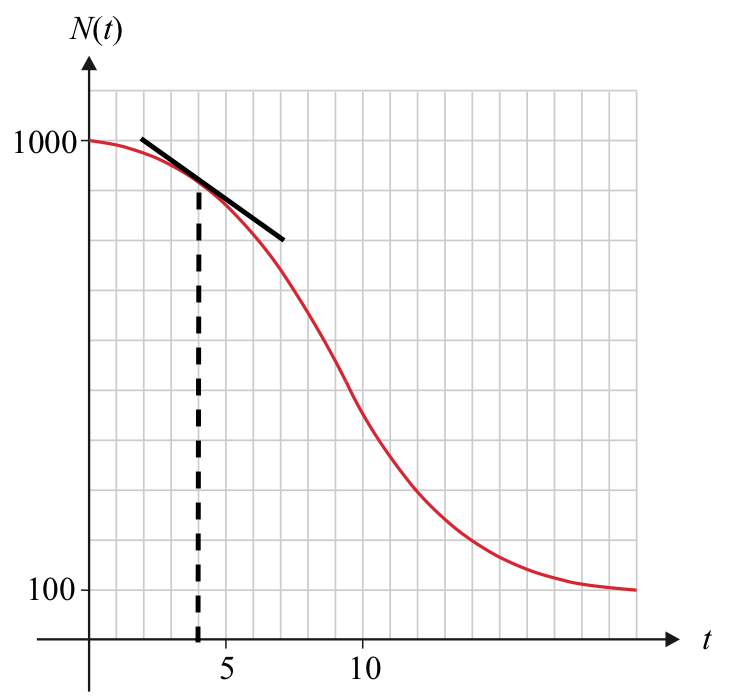
   Det ses, at hældningen = N'(a) = -200/5 = -40

   N'(a) viser at antallet af individer aftager med 40 i døgnet efter 4 døgn

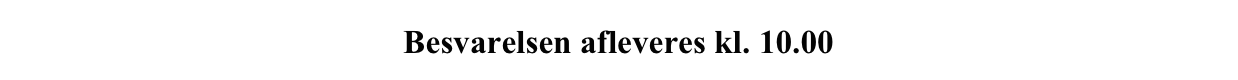
Svar på opgave 7:

1. Man opretter lister med tabellens tal i Ti-Nspire:

   aarstal:={0,1,2,3,4,5,6} ▸ {0,1,2,3,4,5,6}

   tilbagetraek:={62.01,62.25,62.47,62.75,62.77,63.,63.08} ▸ {62.01,62.25,62.47,62.75,62.77,63.,63.08}

   Man bruger kommandoen Beregninger ▸ statistik ▸ statistiske beregninger ▸ lineær regression (mx + b)... og vælger de to oprettede lister som henholdsvis X-liste og Y-liste. Man får:

   

   Dvs. a = 0,1789 og b = 62,08

2. Man definerer f(x) = ax + b ud fra de fundne værdier af a og b:

   f(x):=0.178929*x+62.0818 ▸ Udført

   Man beregner f(2014-2006) = f(8):

   f(2014-2006) ▸ 63.5

   Dvs. i følge modellen bliver tilbagetræknings­alderen i 2014: 63,5 år

3. Man skal løse ligningen f(x-2006) = 65. Man får i Ti-Nspire:

   solve(f(x-2006)=65,x) ▸ x=2022.3

   Man laver en beregning på begge sider af det fundne tal, for at se hvordan det skal afrundes:

   f(2022-2006) ▸ 64.9

   f(2023-2006) ▸ 65.1

   Dvs. i følge modellen oversiger tilbagetræknings­alderen 65 år i 2023

Svar på opgave 8:

1. Man kalder vinkel A for a, vinkel B for b og bruger cosinusrelationerne i Ti-Nspire:

   

   

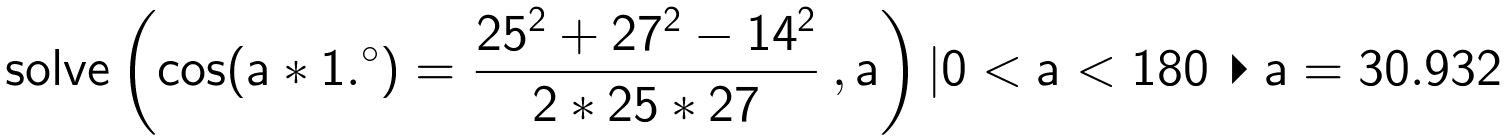
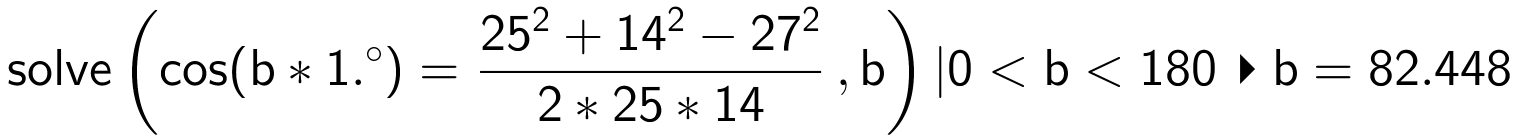
   Dvs. ∠A = 30,9 og ∠B = 82,4

2. Arealet er 0,5·højde·grundlinje = (1/2)·25·sin(30,932°)·27 = 173,5

   V_B findes ved hjælp af sinusrelationen, idet v_B er den modstående side til vinkel A og AB er den modstående side til en vinkel, der er (180° - ∠A - 0,5·∠B). Man får i Ti-Nspire:

   

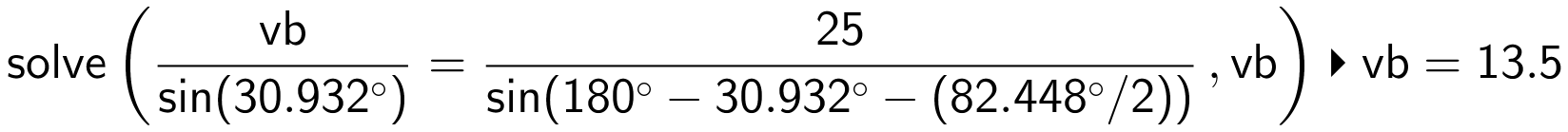
   Dvs. v_B = 13,5

Svar på opgave 9:

1. 12 er antallet af gram i 2014 ved start. 0,97 er fremskrivningsfaktoren som massen af stof hvert år ganges med for at få den nye masse af stof.

2. T_0,5 = ln(0,5)/ln(0,97) år = 22.8 år

Svar på opgave 10:

1. f(x):=2*x³-57*x²-120*x-5 ▸ Udført

   tangentLine(f(x),x,1)=y ▸ 48-228*x=y

   Dvs. tangenten gennem P har ligningen: y = -228x + 48

2. Man skal bestemme fortegn for f´(x). Det gøres i Ti-Nspire med solve og derivative kommandoerne:

   solve(derivative(f(x),x)<0,x) ▸ −1<x<20

   solve(derivative(f(x),x)>0,x) ▸ x<−1 or x>20

   Dvs. f(x) er voksende for: x < −1

   f(x) er aftagende for: −1 < x < 20

   f(x) er voksende for: x > 20

Svar på opgave 11:

1. Man skal finde F(x) = det ubestemte integrale til f(x). Man skal derefter løse F(4) + k = 10 med hensyn til k. Det er gjort i Ti-Nspire:

   integral((1/sqrt(x))+2*x,x) ▸ x²+2*√x

   solve(x²+2*sqrt(x)+k=10,k)|x=4 ▸ k=-10

   Man får stamfunktionen: x² + 2·√x - 10, x > 0

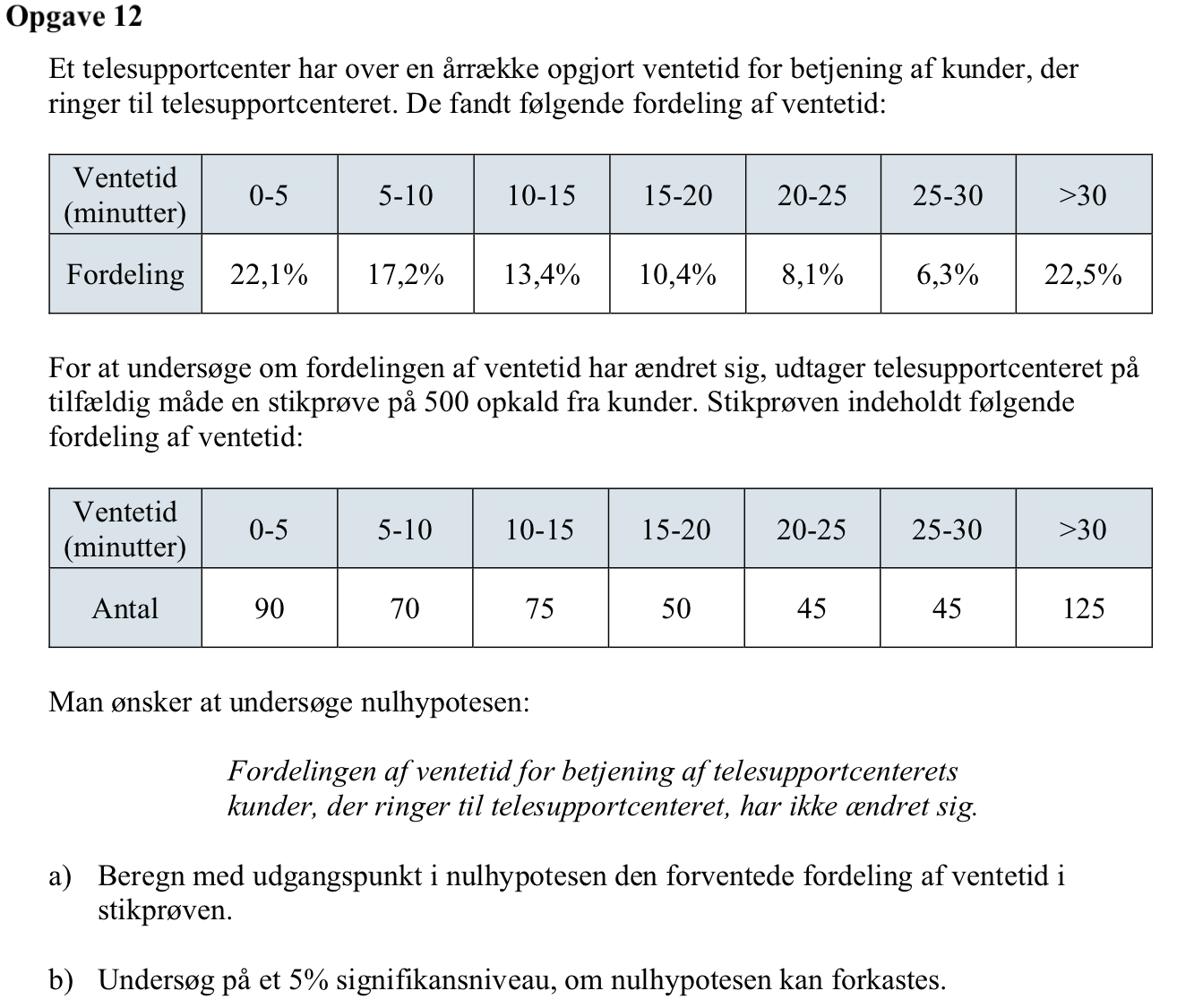
Svar på opgave 12:

1. obs:={90,70,75,50,45,45,125} ▸ {90,70,75,50,45,45,125}

   forvent:=sum(obs)*{(22.1)%,(17.2)%,(13.4)%,(10.4)%,(8.1)%,(6.3)%,(22.5)%} ▸ {110.5,86.,67.,52.,40.5,31.5,112.5}

   Dvs. de forventede værdier er:

   0-5: 110,5 | 5-10: 86,0 | 10-15: 67,0 | 15-20: 52,0 | 20-25: 40,5 | 15-30: 31,5 | >30: 112,5

2. Man laver en goodness-of-fit test med 6 frihedsgrader:

   

   Det ses at PVal = 0,017 = 1,7 %. Da dette er mindre end 5 % forkastes nul-hypotesen.

Svar på opgave 13:

1. Grafen for f er en parabel. Da toppunktet til parablen ligger på anden-aksen i y = 210 har f(x) formen:

   f(x) = a·x² + 210

   Man bruger nu punktet (x,y) = (120,185) på parablen til at beregne a:

   a·120² + 210 = 185 ⇒ a = -0,001736

   Dermed er forskriften for f: f(x) = -0,001736x² + 210

2. Arealet er integralet af f(x) fra x = -120 til x = 120, som findes på Ti-Nspire:

   integral(−0.001736*x²+210,x,−120,120) ▸ 48400.1

   Portens areal er 48.400 cm²