

Svar på opgave 1:
-
3x - 7 = 5 ⇔ 3x = 12 ⇔ x = 4
Svar på opgave 2:
-
f´(x) = 3x2 - 2 ⇒ f´(2) = 3·22 - 2 = 10

Svar på opgave 3:
-
1.134 mio. er befolkningstallet år 2005.
1,014 er fremskrivningsfaktoren man ganger sidste års tal med for at få tallet for det nye år.

Svar på opgave 4:
-
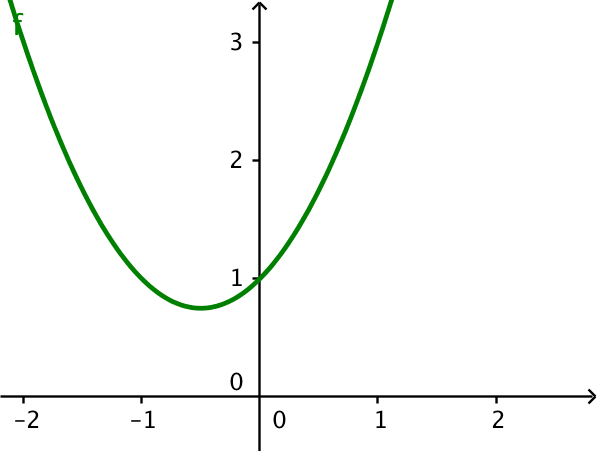
Diskriminanten < 0: ingen skæring med x-aksen,
a > 0: grenene vender opad og
c > 0: parablen skærer den positive del af y-aksen.

Svar på opgave 5:
-
Stamfunktionen til f(x) er F(x) = 6·⅓x3 - 2·½·x2 + k = 2x3 - x2 + k.
Man skal finde det k der gør, at 2·13 - 12 + k = 10 ⇒ k = 9

Svar på opgave 6:
-
Ved hjælp af Pythagoras læresætning får man, at h = 8 m + √[52 - 42]m = 11m
Arealet er 8m·4m + ½·4m·√[52 - 42]m = 32 m2 6 m2 = 38 m2


Svar på opgave 7:
Løsning i Ti-Nspire.
-
f(x) er en aftagende lineær model. Man finder a og b ved at lave lineær regression.
Førest oprettes lister over breddegrad og middeltemperatur:
bredde:={62,64,70,73,78} ▸ {62,64,70,73,78}
middel:={1.,−1.6,−4.2,−7.2,−11.4} ▸ {1.,−1.6,−4.2,−7.2,−11.4}
Man bruger kommandoen Beregninger ▸ statistik ▸ statistiske beregninger ▸ lineær regression (mx + b)... og vælger de to oprettede lister som henholdsvis X-liste og Y-liste. Man får:

Heraf ses (idet m = a), at a = -0,732 og b = 46,09
-
a er det antal grader celsius, som middel-temperaturen ændrer sig med, når man går én breddegrad længere nordpå.
Man skal finde f(66). Man får: f(66) = -0,732·66 + 46,09 °C = -2,19 °C
-
Man skal løse ligningen f(x) = -10 med hensyn til x.
Man får: -0,732·66 + 46,09 °C = -10°C ⇒ x = 76.7° Nordlig bredde
Svar på opgave 8:
Løsning i hånden og Ti-Nspire:
-
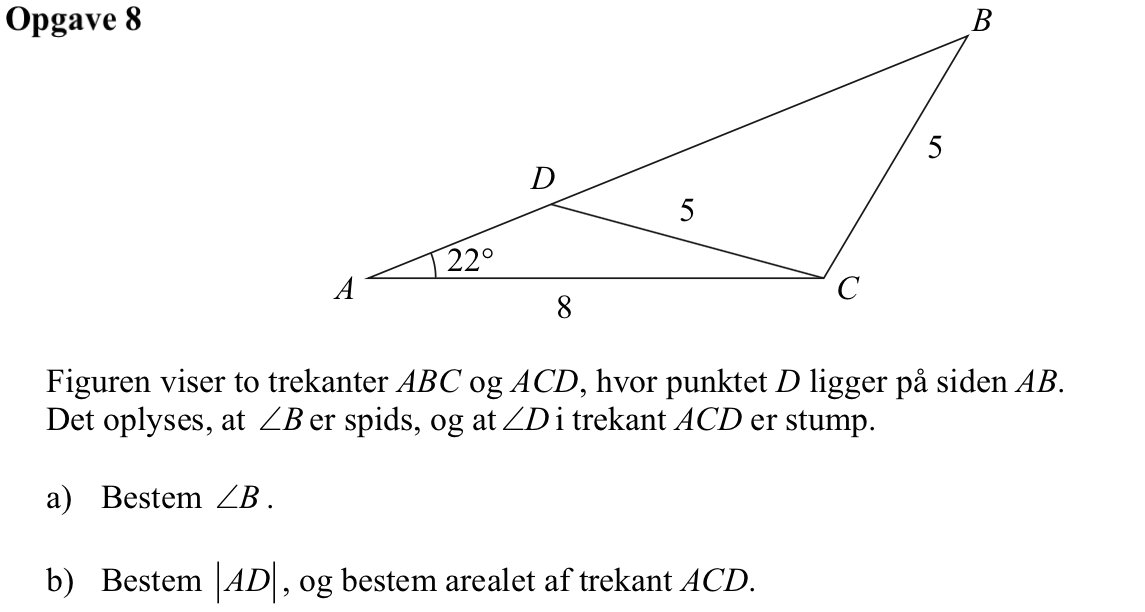
Man bruger sinusrelationen.
sin(∠B)/8 = sin(∠A)/5 ⇒ sin(∠B) = 8·sin(∠22°)/5 ⇒ ∠B = sin-1(0,5994) = 36,8°
-
|AD| = x kan findes ved hjælp af cosinusrelationen. Man bruger Ti-Nspire kommandoen:
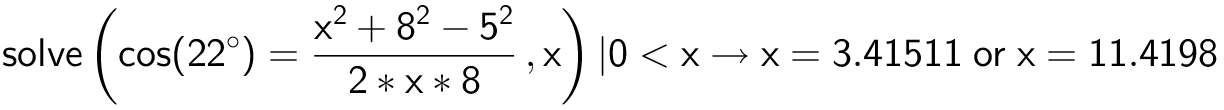
Heraf fås at |AD| = 3,42, da det er den løsning, som gør at ∠D er stump.
Arealet af trekant ACD = ½·8·h, hvor h er højden fra D ned på AC.
Man har at h = |AD|·sin(22°) = 3,415·0,3746 = 1,279
Arealet er ½·8·1,279 = 5.12

Svar på opgave 9:
-
Fra P har man, at f(1) = 2 og fra Q, at f(5) = 7. Det giver to ligninger med to ubekendte som løses med hensyn til a og b i Ti-Nspire:
solve(b*1a=2 and b*5a=7.,a,b) ▸ a=0.778 and b=2.
a = 0.778 og b = 2

Svar på opgave 10:
Løsning i Ti-Nspire.
-
Man definerer c(t) : c(t):=67*(exp(−0.041*t)-exp(−3.1*t)) ▸ Udført
Graf for C(t) (med x i stedet for t):
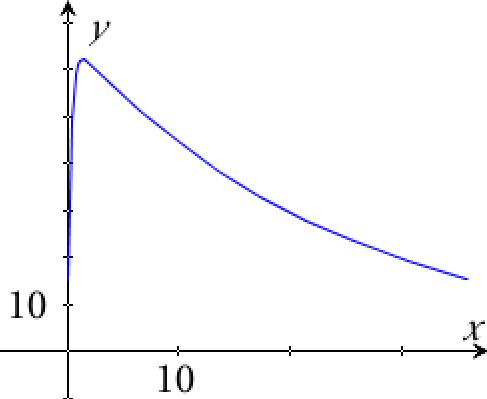
For at finde koncentrationen, bruger man kommandoen: C(20) ▸ 29.5089
Koncentrationen efter 20 timer er 29,5 picogram/mL
-
Man bruger kommandoen: fMax(c(t),t) ▸ t=1.414
Maksimumkoncentration kommer efter 1,41 timer
-
Man bruger kommandoen: solve(c(t)=25,t) ▸ t=0.1539 or t=24.044
Dette viser, at man skal tage en ny pille efter 24,0 timer
Løsningen t = 0,15 er ikke gyldig, da koncentrationen er stigende i denne værdi af t, og man skal finde en værdi af t, hvor koncentrationen er faldende.

Svar på opgave 11:
-
Man bruger Ti-Nspire kommandoen: y=tangentLine((x-7.)*exp(-x),x,2) ▸ y=0.812*x-2.30
Dvs. tangentligningen er y = 0,812x - 2,30
-
Man skal undersøge fortegn for f´(x). Man bruger Ti-Nspire kommandoerne:
solve(derivative((x-7.)*exp(-x),x)<0,x) ▸ x>8
solve(derivative((x-7.)*exp(-x),x)>0,x) ▸ x<8
Første linje viser, at f´(x) < 0 for x > 8, og at f´(x) > 0 for x < 8. Dvs. monotoniforholdene er:
f(x) vokser for x < 8 og aftager for x > 8. X = 8 er et maksimum.
Svar på opgave 12:
Løsning i Ti-Nspire uden regneark.
-
Nulhypotese: kaffetype er uafhængig af nationalitet
Man opretter en matrix med observationer:
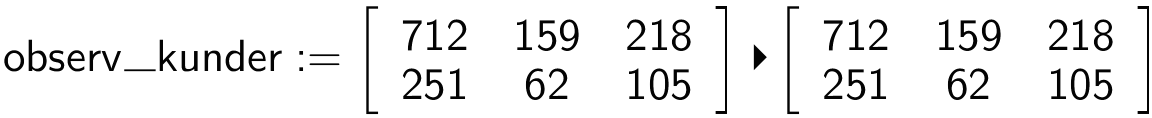
Man vælger (forudsat man er i Noter) menupunktet:
Beregninger ▸ Statistik ▸ Statistiske tests ▸ χ²-uafhængighedstest...
...vælger matricen observ_kunder, trykker OK og får:

Man bruger kommandoen:

Denne matrix er de forventede værdier.
-
Det ses at PVal i ovenstående beregning er 0.08 = 8 % og dermed større end 5 %. Derfor accepteres nulhypotesen.

Svar på opgave 13:
Løsning i Ti-Nspire.
-
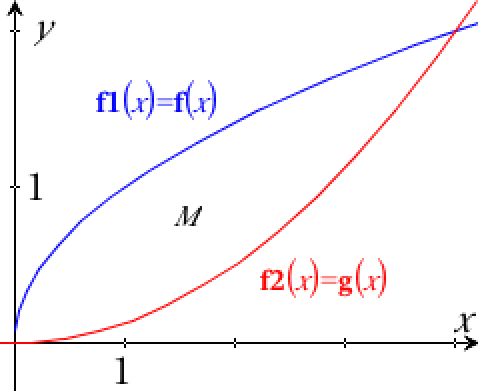
-
Man skal integrere f(x) - g(x) mellem grafernes skæringspunkter.
Man finder skæringspunkterne ved hjælp af kommandoen: solve(f(x)=g(x),x) ▸ x=0 or x=4, dvs. man skal integrere fra x = 0 til x = 4.
Man finder integralet med kommandoen: integral(f(x)-g(x),x,0,4.) ▸ 2.6667
Dvs. M's areal er 2,67