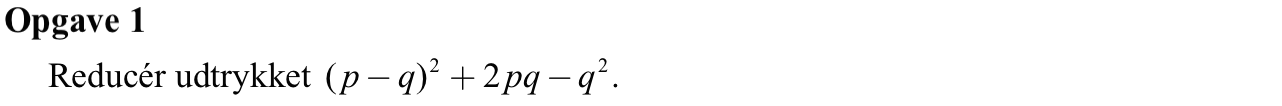
Svar på opgave 1:

1. (p - q)² + 2·p·q - q² =

   (p - q)·(p - q) + 2·p·q - q² =

   p² - 2·p·q + q² + 2·p·q - q² =

   p² + (-2·p·q + 2·p·q) + (q² - q²) =

   p²

Svar på opgave 2:

1. Der er tale om en positiv lineær sammenhæng.

   f(x) = 45x + 100,

   hvor x er antal solgte enheder og f(x) er den samlede pris i kr. 45 er stk. prisen i kr. og 100 er forsendelsesprisen, der er uafhængig af det solgte antal enheder.

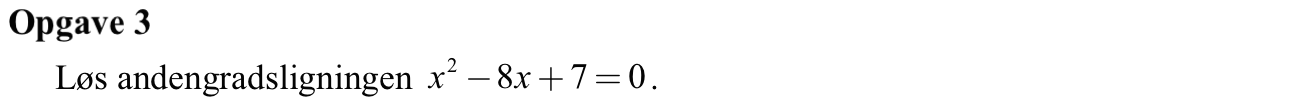
Svar på opgave 3:

1. x² - 8x + 7 = 0 ⇔

   x = 4 ± 0,5·√(64 - 28) ⇔

   x = 4 ± 0,5·√(36) ⇔

   x = 4 ± 0,5·6 ⇔

   x = 4 ± 3 ⇔

   x = 1 ∨ x = 7

Svar på opgave 4:

1. f´(x) = e^x + 2x

Svar på opgave 5:

1. |AB| er hypotenusen i den lille retvinklede trekant. Den kan findes ved hjælp af Pythagoras læresætning: |AB|² = 3² + 4² = 25 ⇒

   |AB| = 5

   Skaleringsfaktoren mellem den store og den lille trekant er |DE|/|BC| = 5/4.

   Omkredsen af den store trekant er lig med skaleringsfaktoren gange omkredsen af den lille.

   Dvs. omkredsen af ADE = (5/4)·(3 + 4 + 5) = (5/4)·12 = 15

Svar på opgave 6:

1. Integralet bliver:

   

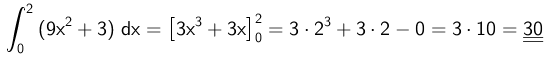
Svar på opgave 7:

Løsning i Ti-Nspire.

1. Førest oprettes lister over antal år efter 1994 (årstal) og affaldsproduktion (affaldsprod):

   årstal:={1994,1996,1998,2000,2002,2004,2006,2008}-1994 ▸ {0,2,4,6,8,10,12,14}

   affaldsprod:={2575,2767,2796,3084,3121,3164,3298,3654} ▸ {2575,2767,2796,3084,3121,3164,3298,3654}

   Man laver eksponentiel regression i Ti-Nspire ved hjælp af kommandoen Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression...

   

   Heraf ses (idet a og b skal byttes om) at a = 1,0223 og b = 2605,3

2. Affaldsproduktionen i 2005 er f(2005-1994) = 2605,3·1,0223^2005-1994 tons = 2605,3·1,0223¹¹ tons = 3322 tons

   Det år, hvor affaldsproduktionen var 3500 tons findes ved hjælp af solve kommandoen i Ti-Nspire:

   solve(f1(x)=3500,x) ▸ x=13.37 (f1(x) skabes automatisk, når man laver regression i Ti-Nspire)

   Dvs. året er 1994 + 13 = 2007,

   hvilket også kan aflæses af tabellen, da tallet for 2006 er mindre end 3500 og tallet for 2008 er større.

3. Modellens forudsigelse for 2009 er tallet f(2009-1994) = f(15) = 2605,3·1,0223¹⁵ tons = 3627 tons

   Dette er kun ca. 6 % større end det faktiske tal på 3437. Modellen kan dermed godt bruges, hvis man accepterer 6%'s unøjagtighed.

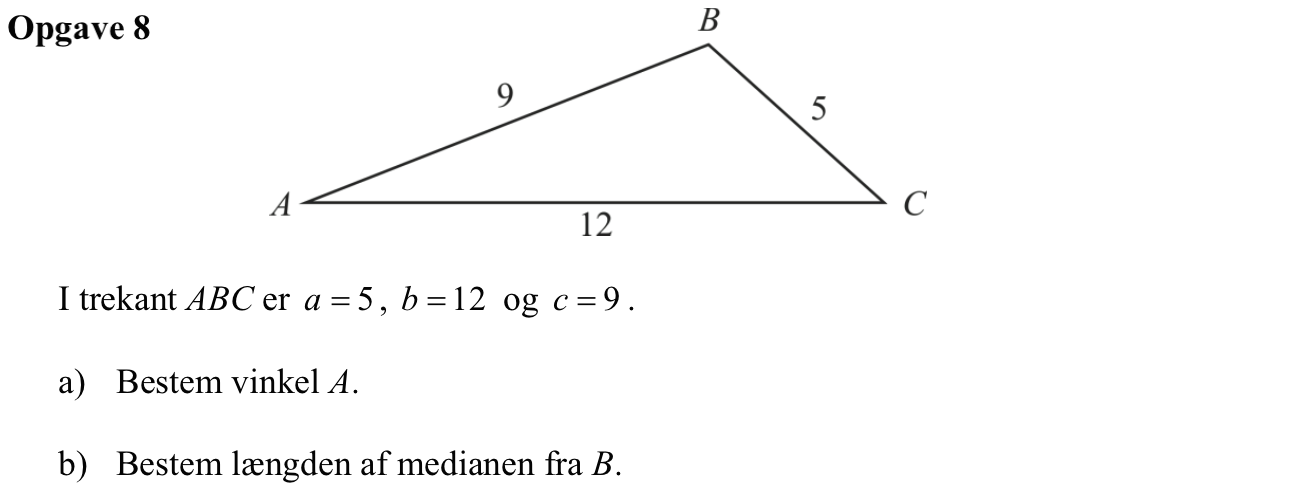
Svar på opgave 8:

1. Man bruger en cosinusrelation, da man kender alle sider, men ingen vinkler. Man finder ∠A som x i Ti-Nspire

   solve(cos(x*1.°)=(12²+9²-5²)/(2*12*9),x)|0≤x≤180 ▸ x=22.19

   Dvs. ∠A = 22,2°

2. Nedenunder er medianen tegnet som siden BD i trekant ABD.

   

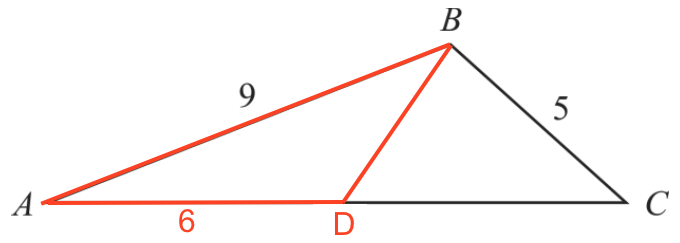
   Man skal finde |BD|, idet man ved, at |AB| = 9 og |AD| = 6. Man bruger en cosinusrelation, da man kender vinkel A og to sider. Man får følgende i Ti-Nspire, hvor længden af medianen kaldes x:

   solve(cos(22.1916°)=((9²+6²-x²)/(2*9*6)),x)|x>0 ▸ x=4.123

   Dvs medianen BD har længden 4,1

Svar på opgave 9:

1. Man opretter h(t) i Ti-Nspire:

   h(t):=(3128-40*t)^0.4 ▸ Udført

   Man skal finde h(20), som er højden efter 20 sekunder:

   h(20) ▸ 22.22

   Dvs. højden efter 20 sekunder er 22,2 cm

   Den tid der går før væske højden er 5 cm findes ved hjælp af solve-kommandoen i Ti-Nspire:

   solve(h(t)=5,t)|0≤t≤78.2 ▸ t=76.80

   Dvs. der går 76,8 sekunder før væskehøjden er 5 cm

2. Man finder f´(20) i Ti-Nspire ved hjælp af kommandoen:

   derivative(h(t),t)|t=20 ▸ −0.1527

   Dette viser, at den hastighed, som væskehøjden ændres med efter 20 sekunder, er

   −0,15 cm/s, hvor minustegnet betyder, at der tale om et fald i højden.

Svar på opgave 10:

1. Man definerer f(x) i Ti-Nspire:

   f(x):=0.25*x⁴-3*x³+12*x²-16*x ▸ Udført

   Man finder tangenten gennem punktet (5,f(5)) ved hjælp af kommandoen tangentLine, hvor man skriver "y=" foran for at hele ligningen med i resultatet:

   y=tangentLine(f(x),x,5) ▸ y=4*x-18.75

   Dvs. tangenten gennem punktet (5,f(5)) har ligningen: y = 4x - 18,75

2. Monotoniforholdene bestemmes med følgende Ti-Nspire-kommandoer, der finder de x hvor f´(x) < 0, henholdsvis de x hvor f´(x) > 0 :

   solve(derivative(f(x),x)<0,x) ▸ x<1.

   solve(derivative(f(x),x)>0,x) ▸ x>1. and x≠4.

   Dvs. at f aftager for x mindre end 1 og vokser for x større end 1.

   For x = 4 har f vandret vendetangent, men f er stadig voksende, dog ikke strengt voksende.

Svar på opgave 11:

1. Graferne for f og g, området M er tegnet nedenunder i Geogebra.

   

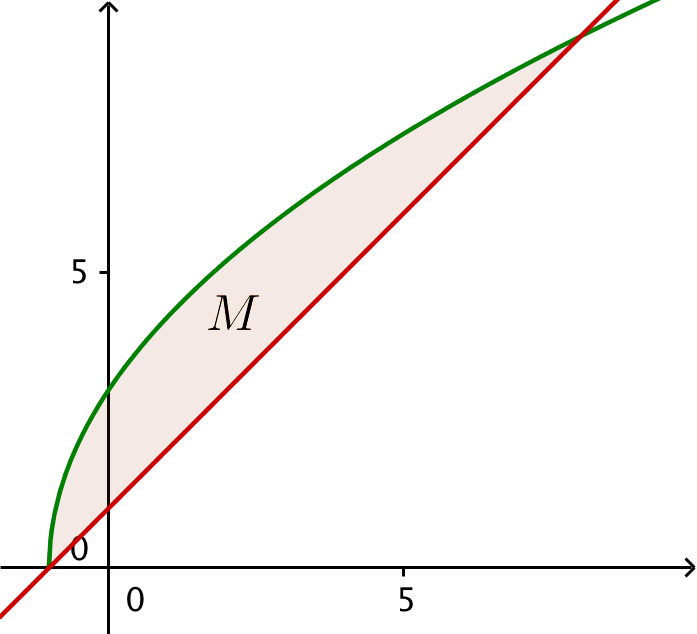
   Arealet af M er integralet af f - g fra x = -1 til x = 8, som er x-værdien for det højre skæringspunkt mellem de to grafer. Dette giver i Ti-Nspire:

   Integral(3*(x+1)^0.5-(x+1),x,−1,8) ▸ 13.5

   Dvs. arealet er 13,5

Svar på opgave 12:

Løsning i Ti-Nspire uden regneark.

1. Man opretter en matrix med observationer:

   observeret:={30,68,124,198,279,225,76} ▸ {30,68,124,198,279,225,76}

   Man opretter ligeledes en liste med frekvenser over karaktererne

   frekvens:={0.0014,0.0743,0.1096,0.2204,0.3123,0.1983,0.0837} ▸ {0.0014,0.0743,0.1096,0.2204,0.3123,0.1983,0.0837}

   Endelig oprettes en liste med forventede værdier ved at gange summen af antallet af observarioner med frekvanserne:

   forventet:=sum(observeret)*frekvens ▸ {1.4,74.3,109.6,220.4,312.3,198.3,83.7}

   Dvs. de forventede værdier er Karakter:antal = -3:1,4 | 00:74,3 | 02:109,6 | 4:220,4 | 7: 312,3 | 10:198,3 | 12:83,7|

2. Man laver nu en Goodnes of Fit test på observerede antal og forventede antal ved hjælp af følgende kommando i Ti-Nspire:

   Beregninger ▸ Statistik ▸ Statistiske tests ▸ χ²-Goodness of Fit test... som giver

   ...vælger matricen observ_kunder, trykker OK og får:

   χ²GOF observeret,forventet,6: stat.results ▸

   

   PVal = 1,13·10^-125 og dermed mindre end 5%. Derfor forkastes nulhypotesen

Svar på opgave 13:

1. O(x) oprettes i Ti-Nspire:

   o(x):=5.E−4*x³-0.8*x²+837*x+35200 ▸ Udført

   E(x) oprettes:

   e(x):=o(x)/x ▸ Udført

   Forskriften for E(x) udskrives med følgende kommando (for at slippe for parenteser i udtrykket):

   expand(e(x)) ▸ 0.0005*x²-0.8*x+35200./x+837.

   Dvs. funktionsudtrykket bliver E(x) = 0,0005·x² - 0,8·x + 35200/x + 837

   Man finder E(2000):

   e(2000) ▸ 1254.6

   Dvs E(2000) = 1254,6

2. Man løser ligningen O'(x) = E(x) med hensyn til x i Ti-Nspire:

   solve(derivative(o(x),x)=e(x),x) ▸ x=848.85

   Dvs. de mindste enhedsomkostninger forekommer ved en produktion på 849 stk.