Svar på opgave 1:

1. I det sidste felt skal der stå 4·5² = 100

   

Svar på opgave 2:

1. −15x + 5y - 45 = 0 ⇔

   5y = 15x + 45 ⇔

   y = 3x + 9,

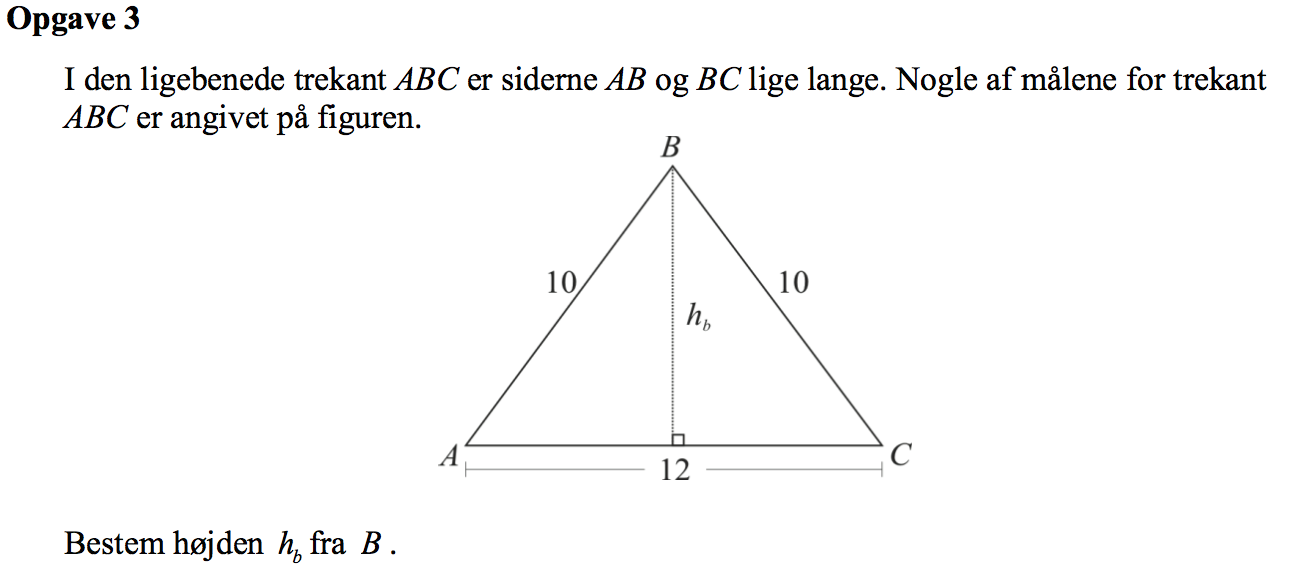
Svar på opgave 3:

1. Man indfører D, som er forpunktet for højden. |DC| = 12/2 = 6.

   

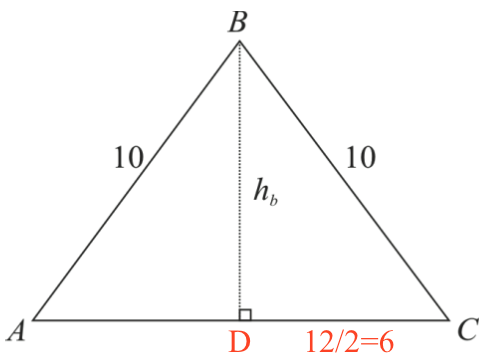
   h_b = |CD| findes ved hjælp af Pythagoras læresætning: (h_b)² + 6² = 10² ⇒

   

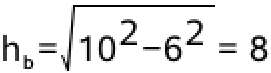
   Dvs. h_b = 8

Svar på opgave 4:

1. 2x² - 8 = 0 ⇔

   x² - 4 = 0 ⇔

   x² = 4 ⇔

   |x| = √4 ⇔

   x = -2 ∨ x = 2

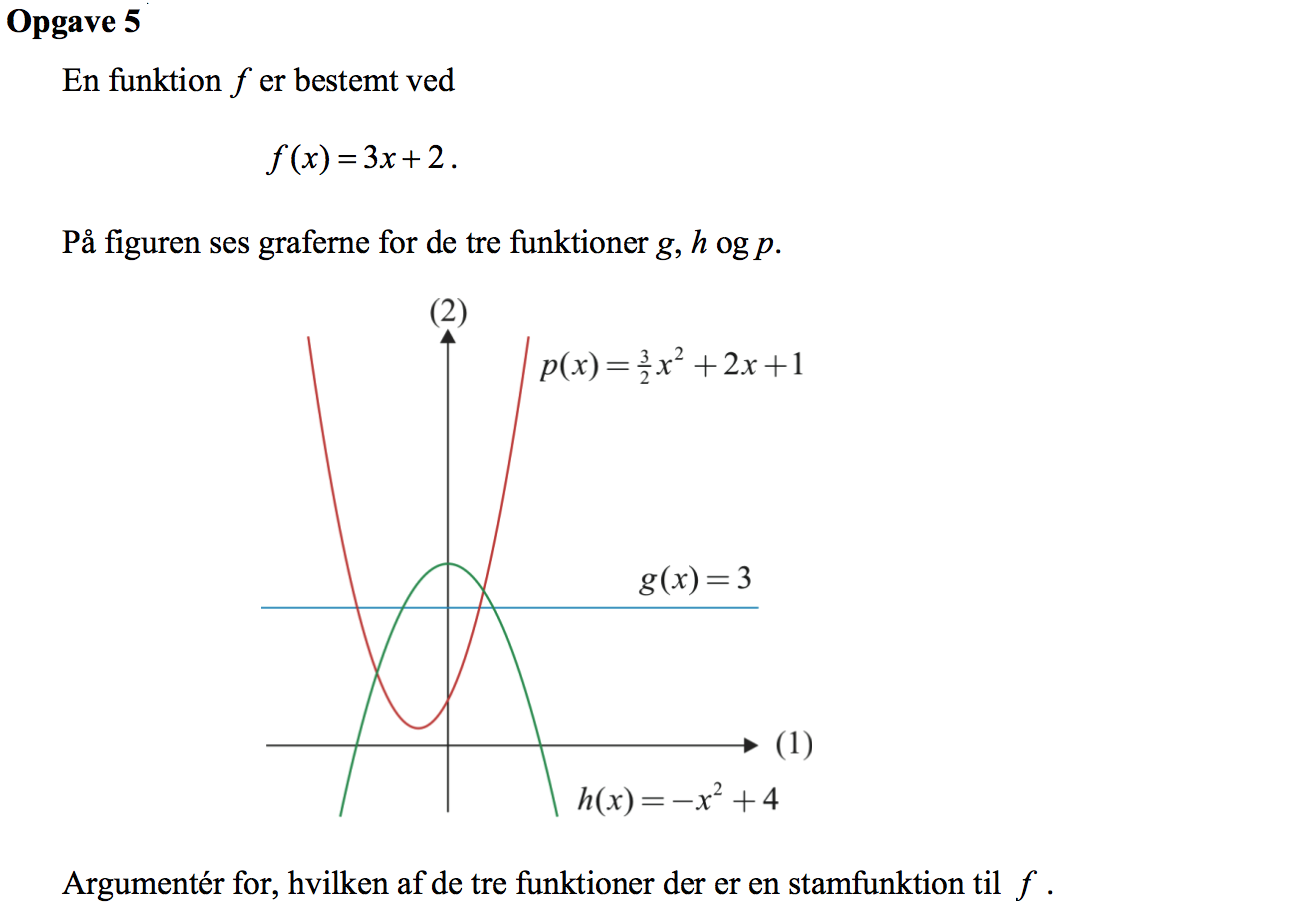
Svar på opgave 5:

1. P(x) er stamfunktion til f, fordi p'(x) = f(x). Man har nemlig: [(3/2)x² + 2x + 1]' = 3x + 2

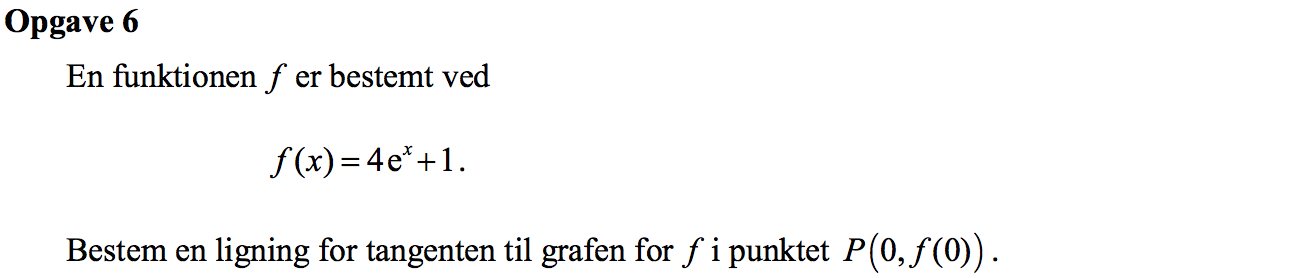
Svar på opgave 6:

1. Ligningen for tangenten er y = f´(0)·(x - 0) + f(0)

   f´(x) = 4e^x ⇒ f´(0) = 4·e⁰ = 4

   f(0) = 4·e⁰ = 1 = 5. Man får heraf følgende ligning for tangenten:

   y = 4·(x - 0) + 5 ⇔

   y = 4·x + 5

Svar på opgave 7:

Løsning i Ti-Nspire.

1. Man opretter lister med antal ynglende par pr. acre (antal_par) og gennemsnitlig kuldstørrelse (kuldstørrelse). Dette gøres i Ti-Nspire:

   

   

   Ud fra listerne laver man en lineær regression (Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Lineær regression (mx+b)... her vælger man de to lister). Man får:

   

   Heraf ses (idet a svarer til m i Ti-Nspire) at a = −0,0097 og b = 3,810

2. Ti-Nspire opretter funktionen f1(x) som er lig med den lineære regressionsfunktion. Man skal løse ligningen f1(x) = 3,0 med hensyn til x:

   

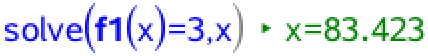
   Dvs. antallet af ynglende par er oppe på 83, når kuldstørrelsen er 3,0

Svar på opgave 8:

1. Vinklen på 43° ved b kaldes w. Siden AC forlænges ud over både A og C og BC forlænges ud over C. I krydset ved C dannes de to topvinkler v og u. Dette er vist nedenunder:

   

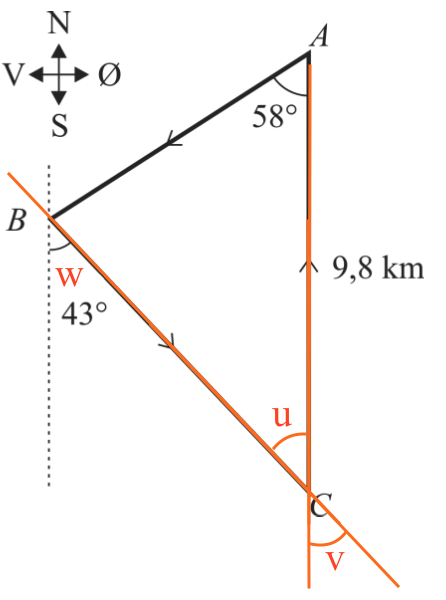
   Vinklen v er ensliggende med w. Da AC og dens forlængning er parallel med kysten, gælder, at v = w. Da u og v er topvinkler i et kryds mellem to rette linjer gælder desuden, at u = v. Dermed er u = ∠ACB = w = 43°.

2. Man skal finde arealet af ΔABC. Arealet er 0,5·grundlinje·højde. Som grundlinje vælges BC. |BC| findes ved hjælp af en sinusrelation i Ti-Nspire. Vinklen A findes ved hjælp af reglen om at vinkelsummen i en trekant er 180°:

   solve(sin(58.°)/bc=sin(180°-58°-43°)/9.8,bc) ▸ bc=8.46642

   Højden i A = |AC|·sin(∠A) = 9.8·sin(43.°) = 6,6836

   Dvs. areal = 0,5·8,4664·6,6836 = 28,29

Svar på opgave 9:

1. Den eksponentielle udvikling følger formlen y(x) = b·a^x hvor y er mængden af affald i tons, b er mængden af affald i 1994, a er 1 + r, hvor r er vækstraten og x er antal år efter 1994. Man skal finde r, når man ved at y(2004-1994) = y(10) = 13.359.000. Dette gøres i Ti-Nspire:

   solve(11105000.*(1+r)^(10)=13359000,r)|r>0 ▸ r=0.018651

   Dvs. vækstraten = 0,01865 = 0,01865·100 % = 1,865 %.

2. Modellen er y = 11105000·1,01865^x, x≥0, hvor y og x er beskrevet ovenfor.

3. Fordoblingstiden er ln(2)/ln(1.01865) år = 37,5 år

Svar på opgave 10:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=1097.9-35.8309*x+0.398778*x²-0.00150341*x³ ▸ Udført

   Nedenfor er grafen tegnet i Ti-Nspire:

   

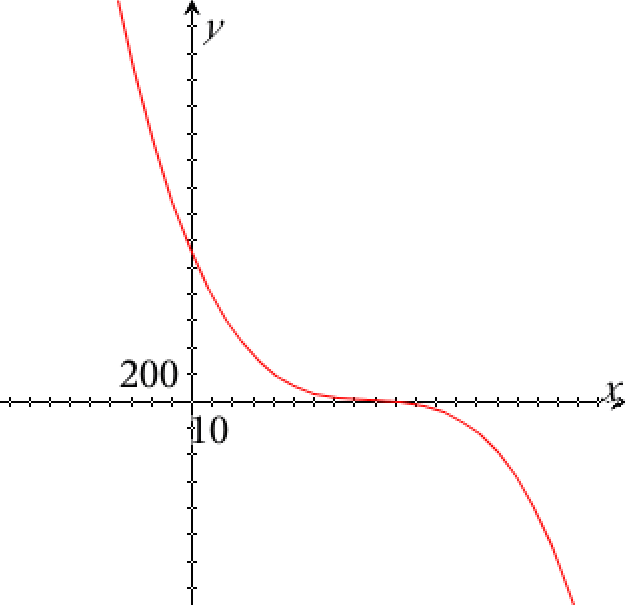
   Man skal beregne f(90) og får: f(90) ▸ 7.23491

   Dvs. der går 7,2 timer får temperaturen er 90°F

2. Man skal løse ligningen f(x) = 2. Dette gøres i TI-Nspire:

   solve(f(x)=2,x) ▸ x=97.3089

   Dvs. temperaturen er 97,3° F efter 2 timer.

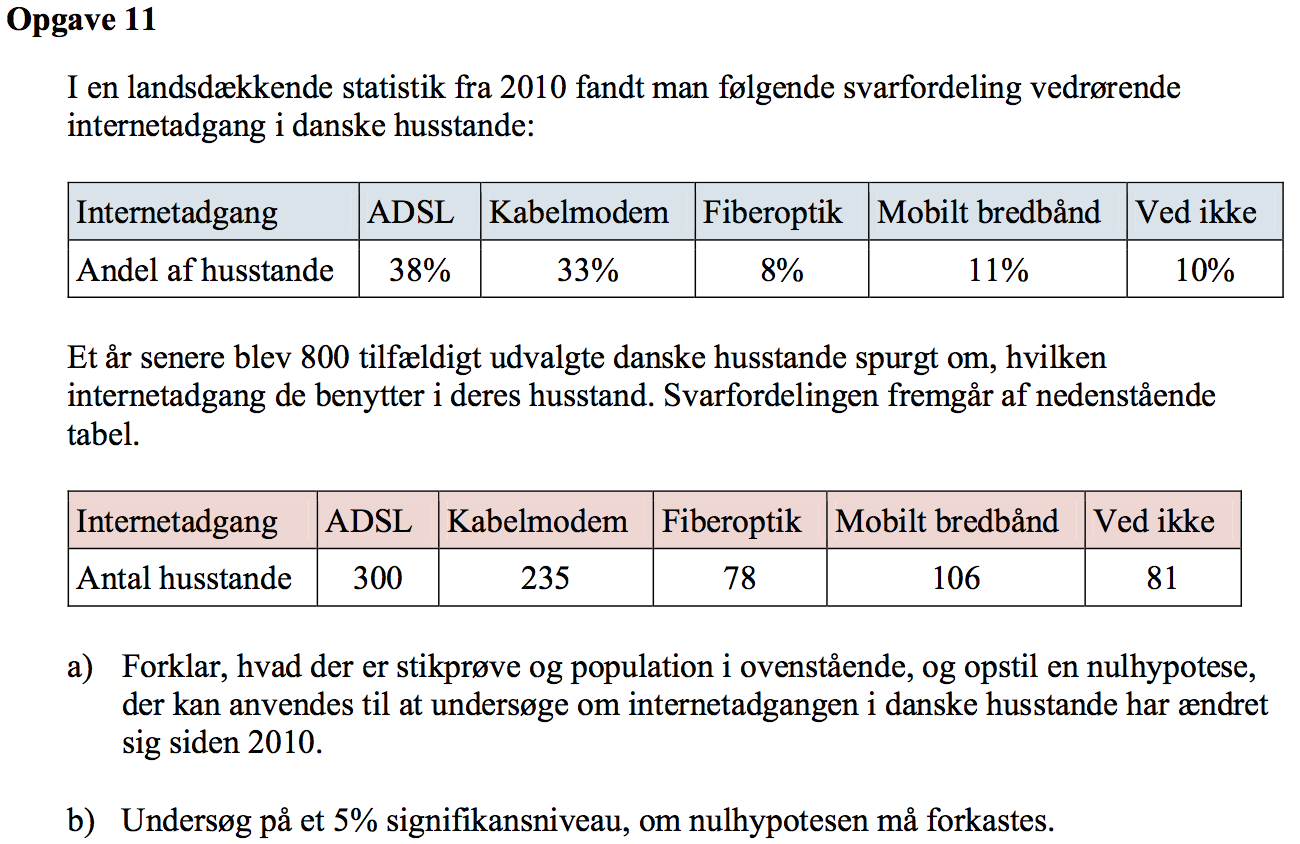
Svar på opgave 11:

1. Den landsdækkende statistik er populationen, mens de 800 hustande er stikprøven.

   Nulhypotesen er at stikprøven stemmer overens med den landsdækkende undersøgelse.

2. Man opretter lister med de forventede værdier beregnet ud fra landsundersøgelsen (kaldet forventet) og en med observerede værdier fra stikprøven (kaldet observeret). Dette er gjort i Ti-Nspire:

   

   Man laver en Goodness-of-fit chi-i-anden test i Ti-Nspire på de to lister. Dette gøres med kommandoen Beregninger ▸ Statistik ▸ Statistiske tests ▸ χ²-Goodness of fit test...

   

   Her ses at p-værdien (PVal) = 0,04, som er mindre 5 % (= 0,05). Dermed forkastes nul-hypotesen.

Svar på opgave 12:

1. Funktionen f(x) oprettes i Ti-Nspire:

   

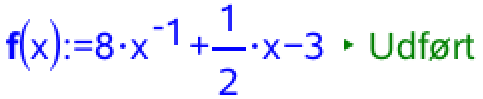
   Man løser ligningen f´(x) = 0, idet man husker, at x er større end 0:

   

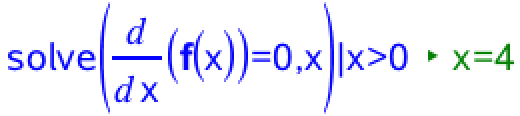
   Dvs. f´(x) = 0 for x = 4

   For at bestemme monotoniforholdene for f laver man en fortegnsundersøgelse for f´(x) omkring dennes nulpunkt:

   

   Dvs. f´(3) = -0,39 < 0 og f´(5) = 0,18 > 0. Dermed er f aftagende for x < 4 og voksende for x > 4

   Nedenunder er vist en graf for f(x) omkring x = 4 til at anskueliggøre monotoniforholdene:

   

2. Man opretter g(x) i Ti-Nspire:

   

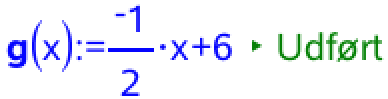
   Graferne for f(x) og g(x) tegnes i Ti-Nspire:

   

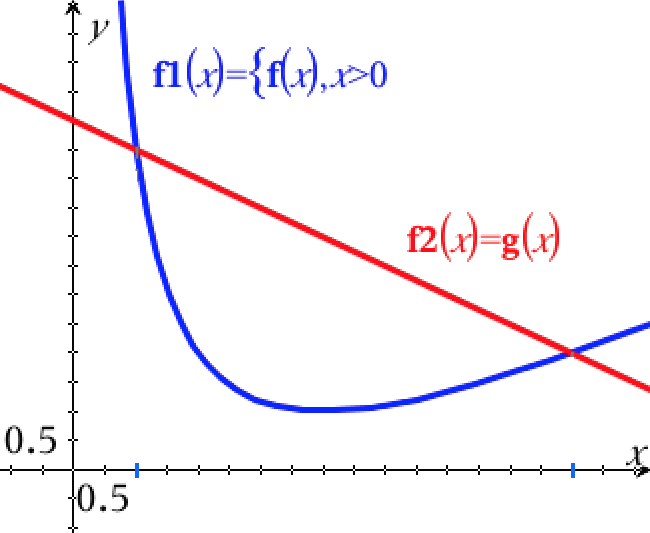
   Man løser ligningen f(x) = g(x) for at finde x-koordinaterne til skæringspunkterne for de to grafer:

   

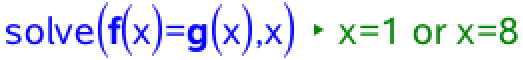
   Dvs. første-koordinaterne for skæringspunkterne i første kvadrant er x = 1 og x = 8

3. Integralet af området M mellem de to grafer er integralet af g(x) - f(x) fra x = 1 til x = 8. Dette beregnes i Ti-Nspire:

   

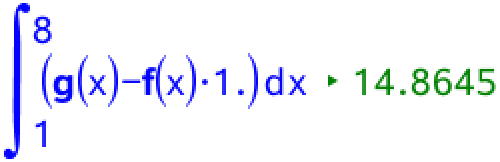
   Dvs. arealet af M er 14,9