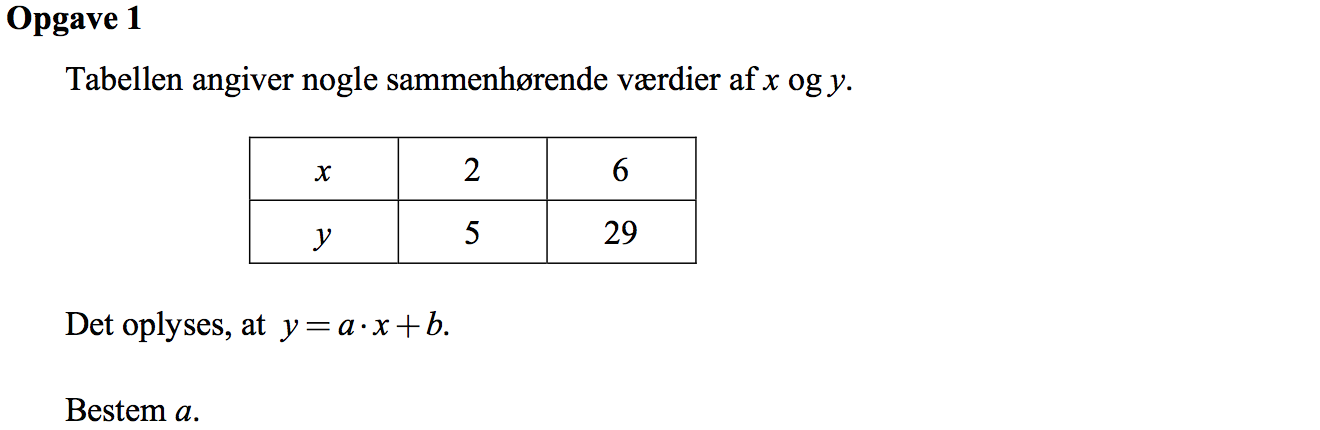
Svar på opgave 1:

1. Tallet a kan bestemmes som hældningen mellem de to punkter (x₁,y₁) og (x₂,y₂). Koordinaterne fremgår af tabellen.

   

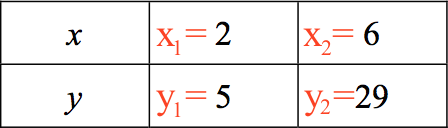
   Man får: a = (y₂ - y₁)/(x₂ - x₁) = (29 - 5)/(6 - 2) = 24/4 = 6

   Dvs. a = 6

Svar på opgave 2:

1. Arealet af trekant ABC er 0,5·|AB|·h_b. Man skal derfor løse ligningen: 0,5·|AB|·h_b = 20 med hensyn til |AB|. Man får:

   0,5·|AB|·h_b = 20 ⇒

   0,5·|AB|·5 = 20 ⇔

   |AB| = 20/(5·0,5) ⇔

   |AB| = 20/2,5 = 8

   Dvs. |AB| = 8

Svar på opgave 3:

1. f(x) = x² - 2x - 3

   Koordinaterne til toppunktet er (-b/2,c-b²/(4a)). Her a = 1, b = -2 og c = -3. Man får

   Toppunkt = (-b/2,c-b²/(4a)) = (-(-2)/2,(-3)-(-2)²/(4·(1))) = (1,-3-4/4) = (1,-4)

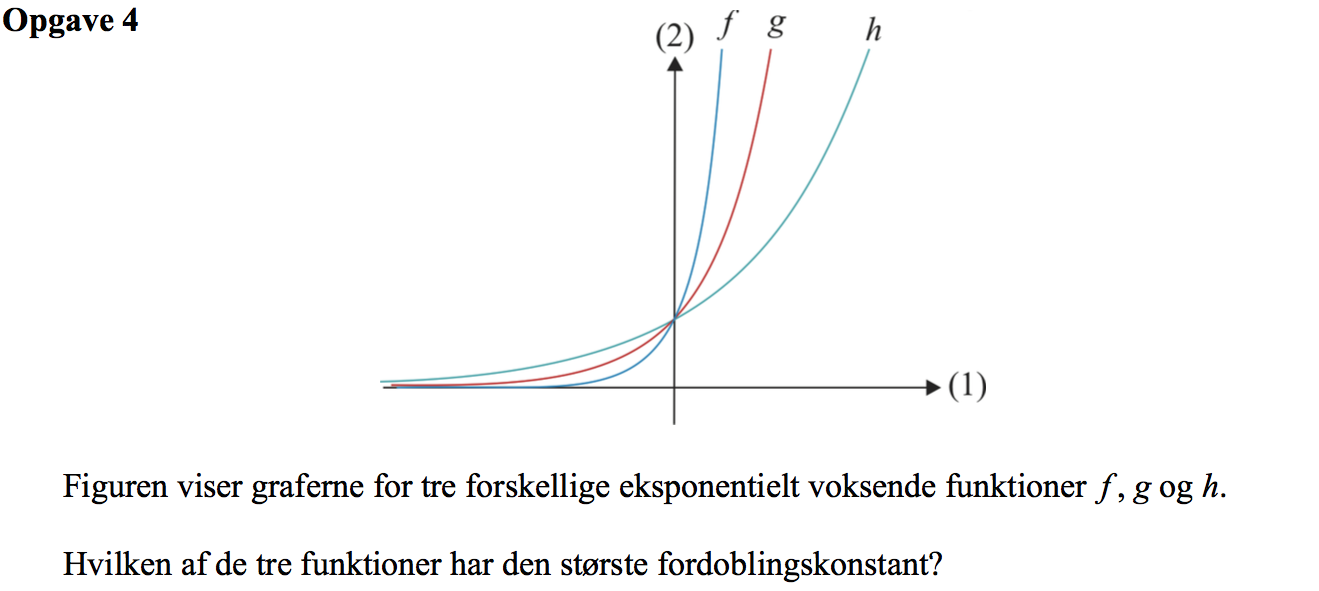
Svar på opgave 4:

1. Fordoblingskonstanten er en værdi, som man skal lægge til x for af fordoble værdien af y. Jo større denne er, jo langsommere vokser funktionen. Dermed har h den største fordoblingskonstant

   

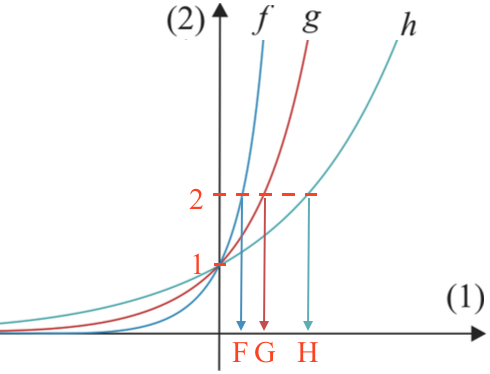
   Figuren ovenfor viser fordoblingskonstanten for hver funktion som henholdsvis F, G og H. H er størst.

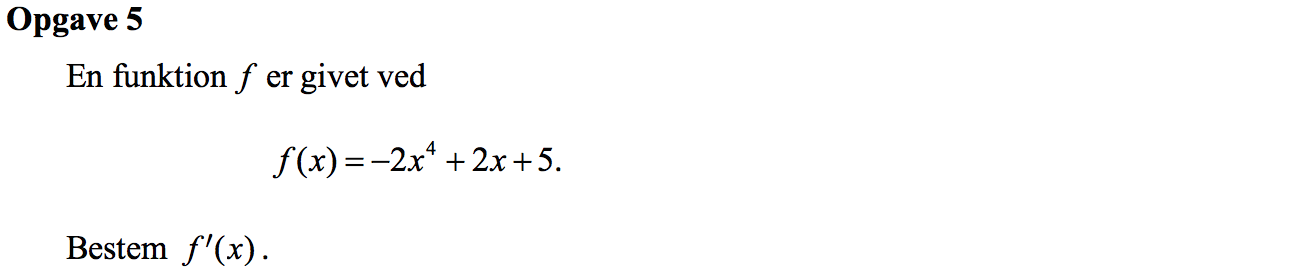
Svar på opgave 5:

1. f´(x) = [−2x⁴ + 2x + 5]' = -8x³ + 2

Svar på opgave 6:

1. Arealet af M er integralet af f(x) fra x = 0 til x = 2. Dette er:

   

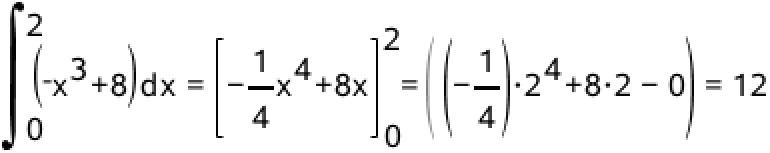
   Dvs. arealet af M er 12

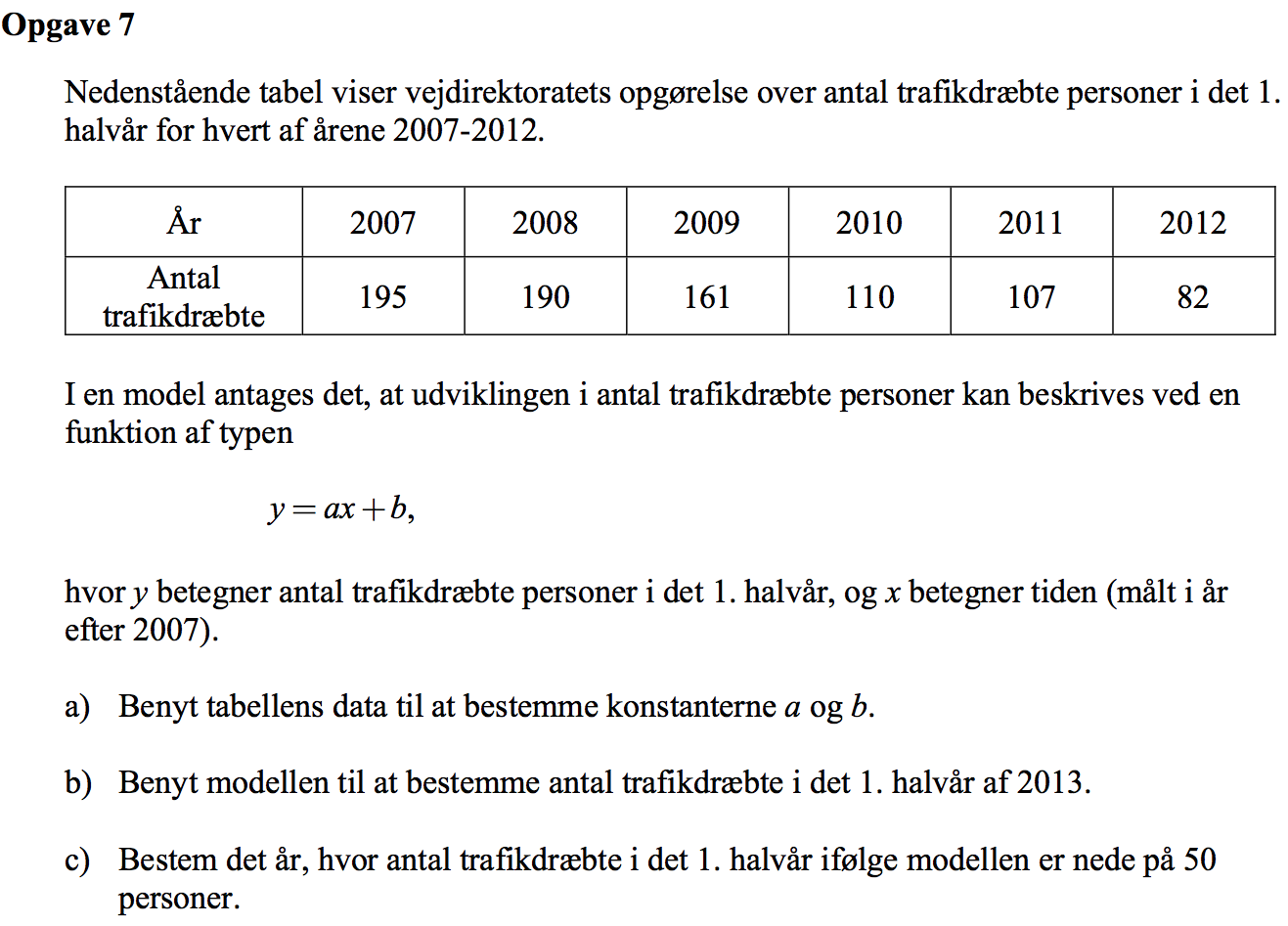
Svar på opgave 7:

1. Man opretter lister med antal år efter 2007 (år) og antal trafikdræbte pr. år (antal). Dette gøres i Ti-Nspire:

   

   Ud fra listerne laver man en lineær regression (Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Lineær regression (mx+b)... her vælger man de to lister). Man får:

   

   Heraf ses (idet a svarer til m i Ti-Nspire), at a = −24,71 og b = 202,6

2. Man bruger den regressions-funktion (kaldet f1(x)), som Ti-Nspire har oprettet og får:

   

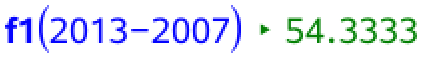
   Dvs. antallet af trafikdræbte er i følge modellen 54 personer i 2013.

3. Man bruger igen f1(x) og løser ligningen f1(x) = 50 med hensyn til x.

   

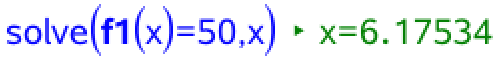
   Dette tal rundes op og lægges til 2007, hvilket giver 2014, som er det år, hvor antallet af trafikdræbte er mindre end eller lig med 50 målt i første halvår.

   Kontrol for afrunding: f1(6) (antallet trafikdræbte i 2013) var 54,3. Det sige, at antallet af dræbte i 2013 (x=6) endnu ikke er kommet under 50. Dermed skal man runde op til x=7 svarende til året 2014.

Svar på opgave 8:

1. Man opretter f(x) of tegner grafen for f i Ti-Nspire:

   f(x):=−0.009425*x²+5.857*x-899.9 ▸ Udført

   

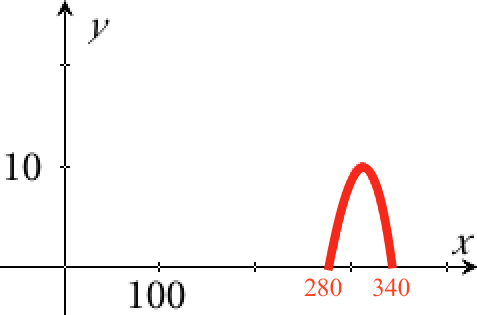
   Man skal herefter finde f(300): f(300) ▸ 8.95

   Dvs. antallet af æg, som en skildpadde med et rygskjold på 300 mm lægger, er 9

2. Man skal løse ligningen f(x) = 6 med hensyn til x og får:

   solve(f(x)=6,x) ▸ x=290.032 or x=331.4

   Dvs. skildpadder med et rygskjold på 290 mm eller 331 mm lægger 6 æg.

Svar på opgave 9:

1. Modellen er y(x)=2038·1,013^x, hvor y(x) er antallet af kræfttilfælde bland kvinder et givent år, x er antal år efter 2010, 2038 er antallet af tilfælde i 2010 og 1,013 er fremskrivningsfaktoren, dvs. det tal, som man skal gange det sidste års antal med for at få det nyes.

2. Man opretter y(x) og m(x) i Ti-Nspire:

   y(x):=2038*(1.013)^x ▸ Udført

   m(x):=2244*(0.99)^x ▸ Udført

   Man løser derpå ligningen y(x) = m(x) med hensyn til x:

   solve(y(x)=m(x),x) ▸ x=4.19266

   Dvs. det årlige antal kræfttilfælde for kvinder har passeret antallet for mænd i 2010 + 5 = 2015

Svar på opgave 10:

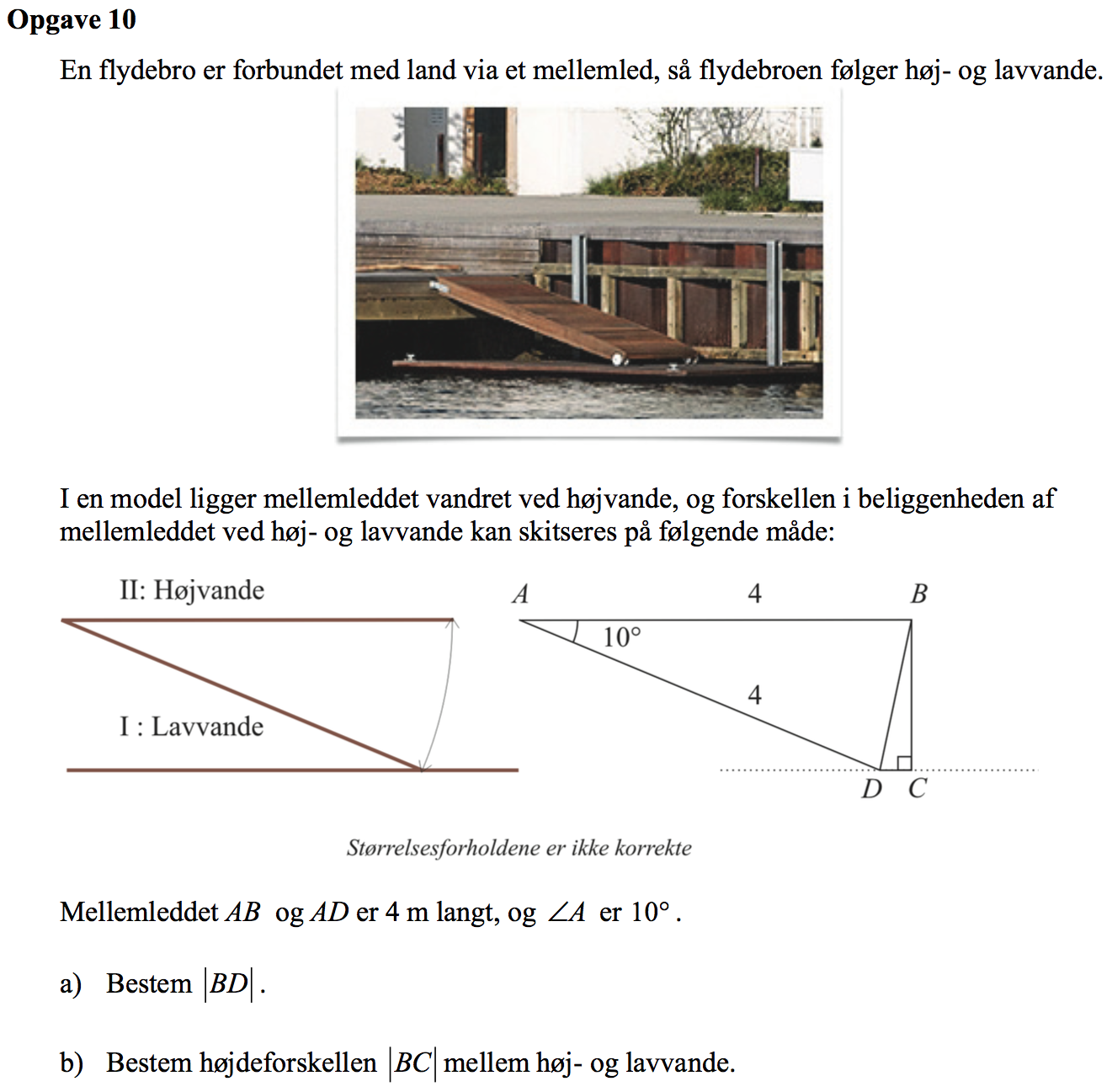
1. Man kan finde |BD| ved hjælp af en cosinusrelation:

   

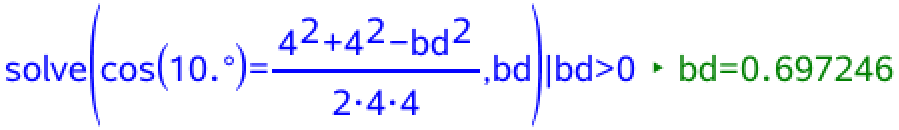
   Dvs. |BD| = 0,697

2. Trekanten BCD er retvinlet. Der gælder at |BC| = |BD|·cos(∠CBD).

   ∠CBD findes på følgende måde:

   ∠ABC = 90°. Da trekant ABD er ligebenet gælder, at ∠ABD = (180°-10°)/2 = 85°. Dermed er ∠CBD = 90° - 85° = 5°.

   Dette er vist på figuren nedenunder:

   

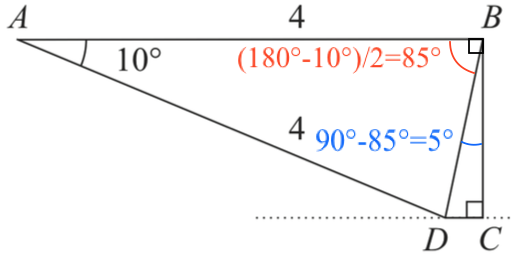
   Man får derfor |BC| = |BD|·cos(∠CBD) = 0,697·cos(5°) = 0,695

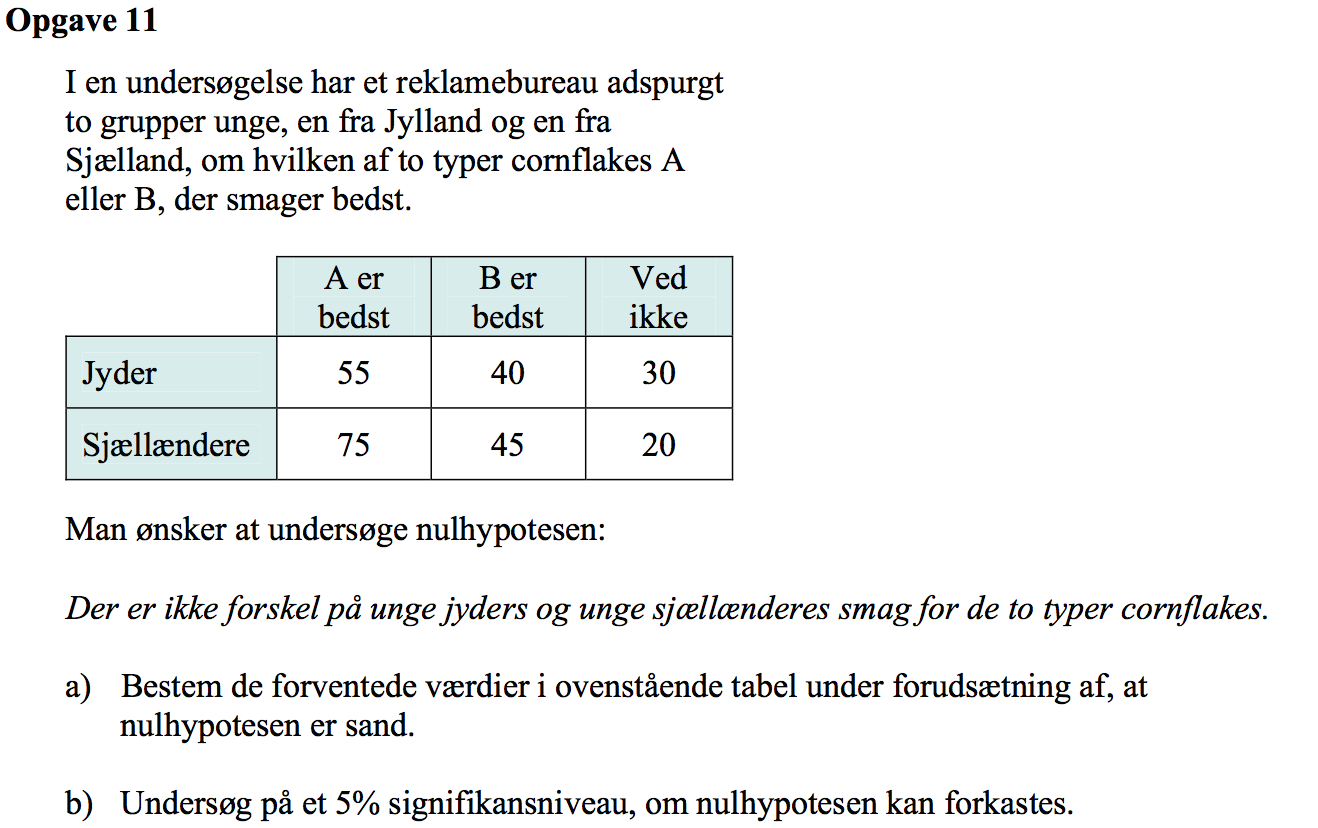
Svar på opgave 11:

1. Man opretter en matrix i Ti-Nspire med de observerede værdier:

   

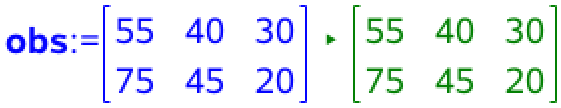
   På denne laves en chi-i-anden uafhængighedstest: (man bruger kommandoen: Beregninger ▸ Statistik ▸ Statistiske test ▸ Χ²-uafhængighedstest...)

   

   Ved hjælp af kommendoen stat.ExpMatrix får man de forventede værdier:

   

2. Af resultatlisten ovenfor ses, at PVal = 0,103 (p-værdien), som er større end 5 % (0,05) og dermed accepteres nul-hypotesen.

Svar på opgave 12:

1. Funktionen f(x) oprettes i Ti-Nspire: f(x):=x³-3*x²-9*x+30 ▸ Udført

   Man løser ligningen f´(x) = 0:

   

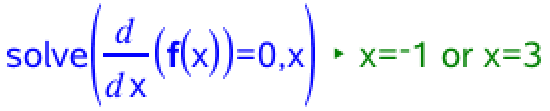
   For at bestemme monotoniforholdene for f laver man en fortegnsundersøgelse for f´(x):

   

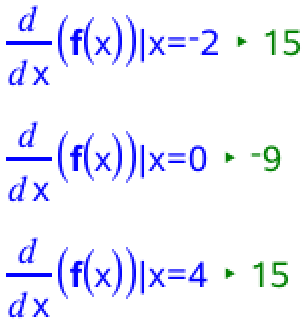
   Dvs. f´(-2)=15>0, f´(0)=-9<0 og f´(4)=15>0.

   Dermed er f voksende for x < -1, aftagende for -1 < x < 3 og voksende for x > 3

2. Tangentens ligning findes i Ti-Nspire ved hjælp af kommandoen tangentLine():

   y=tangentLine(f(x),x,0) ▸ y=30-9*x

   Dvs. ligningen for t₁ er y = -9x + 30

3. Man skal finde det x udover x=0, hvor f´(x) = -9. Dette findes i Ti-Nspire:

   

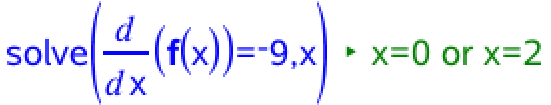
   Det ses at første-koordinaten for t₂ er x = 2