Svar på opgave 1:

1. Siden BC er den ene katete i en retvinklet trekant. Dermed kan |BC| findes ved hjælp af Pythagoras læresætning:

   |BC| = √[10²-6²] = 8

   Da ΔABC og ΔDEF er ensvinklede gælder, at |DE|/|AB| = |DF|/|AC| = |EF|/|BC|.

   |DF|/|AC| = (30/6) = 5. Dvs.

   |DE|/|AB| = 5 ⇒ |DE| = 5·10 = 50

   |EF|/|BC| = 5 ⇒ |EF| = 5·8 = 40

Svar på opgave 2:

1. Formlen for toppunktet af en parabel (der er grafen for et andengradspolynomium) er:

   (-b/(2a),c-b²/(4a)). Her er a = 3, b = -6 og c = 7.

   Dvs. at toppunktet er (-(−6)/(2·3),7-(−6)²/(4·3)) = (1,4)

Svar på opgave 3:

1. Modellen er: y = -0,2·x + 1,5, hvor y er vandmængden målt i liter og x er antal uger efter vasen fyldes.

Svar på opgave 4:

1. Man får: p·h/4 = 4·m ⇔ h = 16·m/p

Svar på opgave 5:

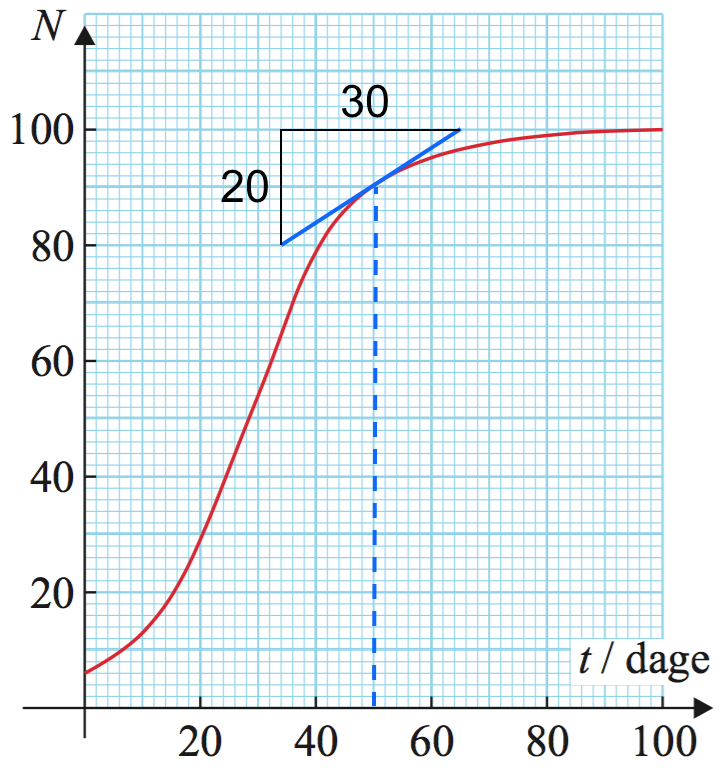
1. Væksthastigheden er hældningen til grafen i x = 50, som er 2/3 = 0,67 stk/uge

   ...det fremgår af billedet:

   

Svar på opgave 6:

1. Funktionen f er en stamfunktion til g, hvis f´(x) = g(x). Man får:

   f´(x) = [2x^3,5 + x² + 10]' = 7·x^2,5 + 2·x = g(x).

   Dvs. f er en stamfunktion til g.

Svar på opgave 7:

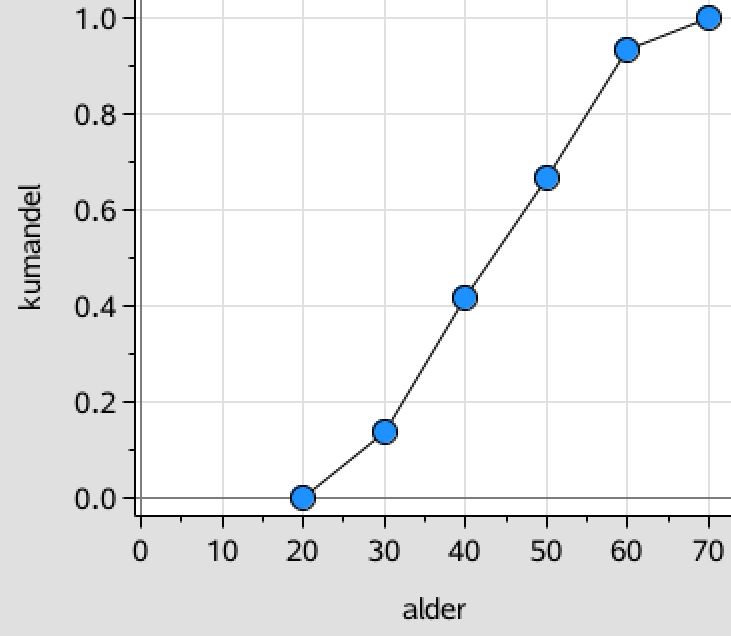
1. Man opretter lister med alder og andelen af hver alder.

   alder:={20,30,40,50,60,70} ▸ {20,30,40,50,60,70}

   andel:={0,(13.6)%,(27.9)%,(25.3)%,(26.5)%,(6.7)%} ▸ {0,0.136,0.279,0.253,0.265,0.067}

   Man finder den kummulerede sum af andelene.

   kumandel:=cumulativeSum(andel) ▸ {0,0.136,0.415,0.668,0.933,1.}

   Dette bruges til at tegne en sumkurve over aldersfordelingen:

   

   For at finde kvartilsættet, så tegner man vandrette linjer for kummulerert andel lig med henholdsvis 25 %, 50 % og 75 %.

   

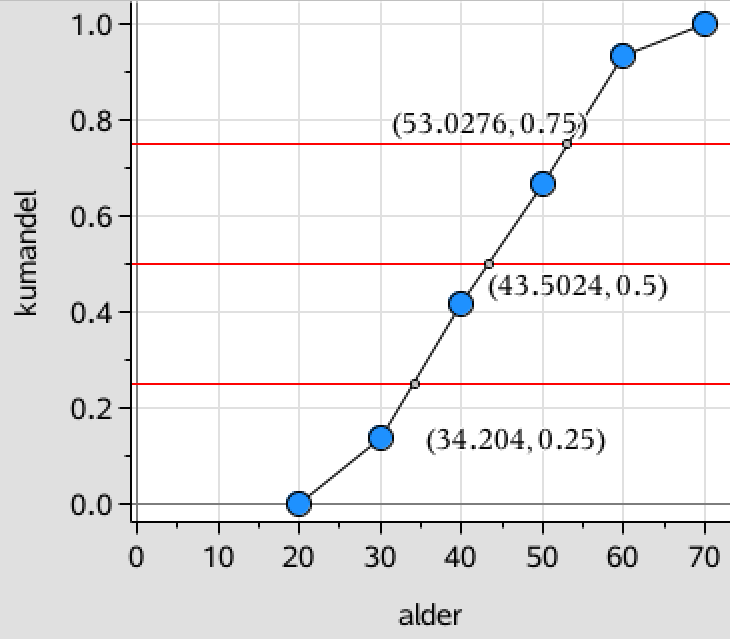
   Ved hjælp af kurven finder man de andele, der svarer til disse kummulerede andele.

   Dvs. som det ses er kvartilsættet: nedre kvartil = 34 år, median = 44 år og øvre kvartil = 53 år

Svar på opgave 8:

1. Man opretter lister med antal år (x) og gæld (f(x)).

   år:={2006,2007,2008,2009,2010}-2006 ▸ {0,1,2,3,4}

   gæld:={50.1,54.8,60.2,65.8,72.1} ▸ {50.1,54.8,60.2,65.8,72.1}

   Ud fra disse lister laves en eksponentialregression:

   ExpReg år,gæld,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",50.0895]
   ["b",1.09538]
   ["r²",0.999945]
   ["r",0.999973]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Af resultattabellen aflæses, at a = 1,095 og b = 50,09

   (Bemærk at Ti-Nspire bruger bogstaverne a og b modsat opgaven).

2. Formlen for fordoblingskonstanten er ln(2)/ln(a). Dette giver her:

   Fordoblingstiden er ln(2)/ln(1.09538) år = 7,61 år

3. Man skal løse ligningen f(x) = 120. Man benytter regressionsfunktionen f1(x), som Ti-Nspire har oprettet og får:

   solve(f1(x)=120,x) ▸ x=9.59038

   Dvs. der går 9,6 år før gælden når op på 120 mia. kr. Dette rundes op til 10 år, og man får dermed årstallet 2006 + 10 = 2016

Svar på opgave 9:

1. Man finder |AB| ved hjælp af en cosinusrelation:

   solve(cos(25.°)=(12²+10²-ab²)/(2*12*10),ab)|ab>0 ▸ ab=5.14647

   Dvs. |AB| = 5,15

   Arealet af ΔABC er en halv grundlinje gange højde. Her vælges grundlinjen |AC| = 12. Højden er |BC|·sin(25°).

   Man får, at arealet af ΔABC er: 0,5·12·10·sin(25°) = 25,4

2. Man skal finde |BC|, når 0,5·12·|BC|·sin(25°) = 15. Man får:

   solve(0.5*12*bc*sin(25.°)=15,bc) ▸ bc=5.9155

   Dvs. |BC| = 5,92

   Man bruger følgende sinusrelation for at finde ∠B: sin(∠A)/|BC|=sin(∠B)/|AC|. Her benytter man, at ∠A = 180° - 25° - ∠B = 155° - ∠B, hvilket følger af reglen om, at vinkelsummen i en trekant er 180°. Man får:

   solve(sin(155.°-b*1.°)/5.9155=sin(b*1.°)/12,b)|0<b<180 ▸ b=134.365

   Dvs. vinkel B er 134,4°

Svar på opgave 10:

1. For at finde a og b skal man løse to ligninger med to ubekendte:

   solve(5.=b*1^a and 15=b*2^a,a,b) ▸ a=1.58496 and b=5.

   Dvs. a = 1,585 og b = 5

   Når x = 8, er y = 5·8^1,58496 = 135,0

Svar på opgave 11:

1. Personens overfladeareal findes ved at indsætte m = 67 og h = 150 i formlen. Man får:

   67^0.425*150^0.725*0.007184 ▸ 1.62224

   Dvs. personens overfladeareal er 1,6 m²

2. For at finde højden skal man løse følgende ligning med hensyn til h: 92^0,425·h^0,725·0,007184 = 2,16. Man får:

   solve(92^0.425*h^0.725*0.007184=2.16,h) ▸ h=184.87

   Dvs. personens højde er 185 cm

Svar på opgave 12:

1. Klodsens volumen er volumenet af en kasse minus volumenet af en cylinder. Kassen har dimensionerne: h, b og l. Cylinderen har højden h og radius 6/2 = 3.

   Man får volumen = h·b·l - h·π·3² = h·b·l - h·π·9

Svar på opgave 13:

1. Man opretter f(x): f(x):=(1-x²)*exp(x) ▸ Udført

   Grafen for f tegnes i Ti-Nspire:

   

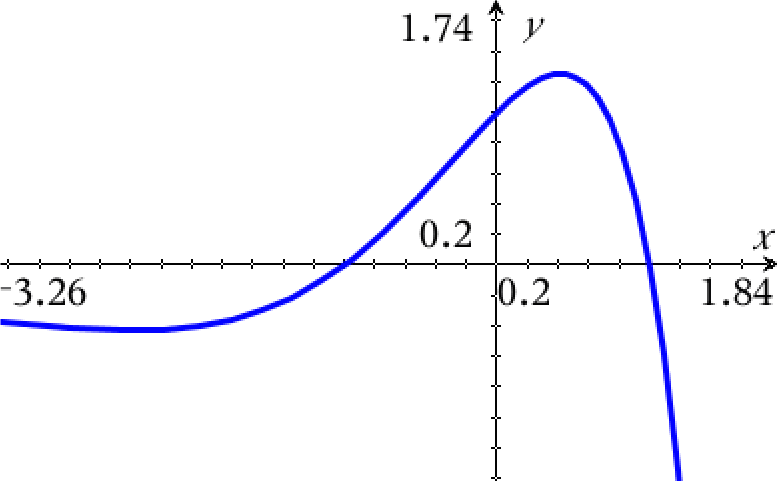
   Man finder tangentens ligning i (1,f(1)) = (1,0) ved hjælp af kommandoen tangentline():

   y=tangentLine(f(x),x,1.) ▸ y=5.43656-5.43656*x

   Dvs. tangents ligning er y = -5,437·x + 5,437

2. For at bestemme monotoniforholdene for f skal man lave en fortegnsundersøgelse af f´(x). Man får:

   solve(derivative(f(x),x)=0.,x) ▸ x=−2.41421 or x=0.414214

   derivative(f(x),x)|x=−3. ▸ −0.099574

   derivative(f(x),x)|x=−2. ▸ 0.135335

   derivative(f(x),x)|x=0.5 ▸ −0.41218

   Dette viser, at f er aftagende for x < −2,414, voksende for −2,414 < x < 0,4142 og aftagende for x > 0,4142

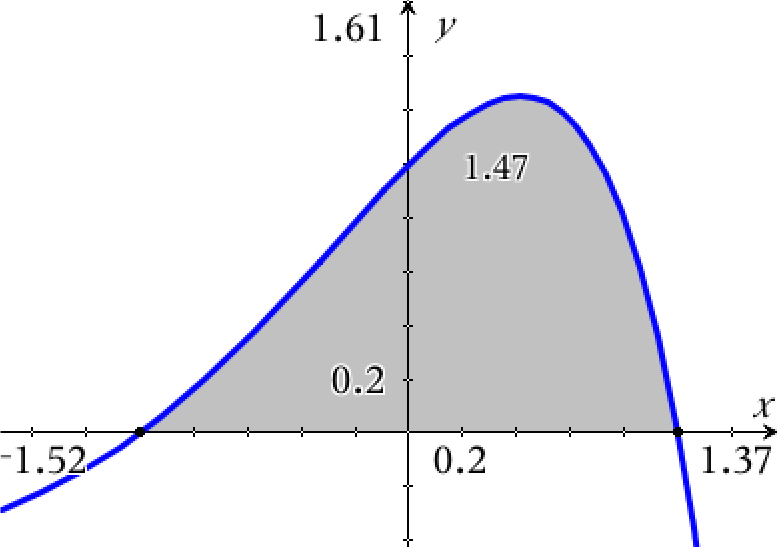
3. Man bestemmer integralet af f fra x = -1 til x = 1:

   integral(f(x)*1.,x,−1,1) ▸ 1.47152

   Dvs. integralet er 1,47

   Dette er arealet under kurven fra x = -1 til x = 1, dvs. arealet under den positive del af funktionen, der er vist nedenunder som det grå område på figuren.

   

Svar på opgave 14:

1. Populationen er alle observationer lagt sammen: 62 + 71 + 140 + 99 = 372

   Nulhypotesen er, at oplevelsen af støjgener er uafhængigt af boligkvarter

   For at teste hypotesen opretter man en matrix med observationerne:

   obs:=[[62,71][140,99]] ▸ [[62,71][140,99]]

   Man foretager en Chi-i-anden uafhængighedstest med en frihedsgrad:

   χ²2way obs: stat.results ▸
   [["Titel","χ²-uafhængighedstest"]
   ["χ²",4.92626]
   ["PVal",0.026452]
   ["df",1.]
   ["ExpMatrix","[...]"]
   ["CompMatrix","[...]"]]

   Da PVal er 0,026, som er mindre end 5 %, forkastes nulhypotesen.