Svar på opgave 1:

1. 2x + 3 = −5x + 17 ⇔

   2x + 5x = 17 - 3 ⇔

   7x = 14 ⇔

   x = 14/7 = 2

Svar på opgave 2:

1. Modellen er f(x) = 25000·(1,045)^x, hvor x er antallet af år efter, at han har oprettet kontoen, og f(x) er indestående på kontoen.

   25000 er startbeløbet og 1,045 er fremskrivningfaktoren på kontoen, dvs. det tal som indeståendet skal ganges med hver år for at få det nye indestående (eller den nye saldo).

Svar på opgave 3:

1. x er den ene katete i en retvinklet trekant, hvor hypotenusen er 10, og den anden katete er 6. Man finder x ved hjælp af Pythagoras læresætning:

   x² + 6² = 10² ⇔

   x² = 10² - 6² ⇔

   x² = 100 - 36 ⇔

   x² = 64 ⇔

   x = √64 = 8

   Arealet af en dragefirkant er 0,5·(diagonal 1)·(diagonal 2) = 0,5·(2·6)·(x + 2x) = 6·3·x = 18·x.

   Dermed er arealet 18·8 = 144

Svar på opgave 4:

1. Eftersom f er en eksponentiel funktion, har den forskriften f(x) = b·a^x, hvor a og b er konstanter.

   Der gælder, at a = ln(2)/ln(T), hvor T er fordoblingskonstanten.

   Dvs. a = ln(2)/ln(8) = ln(2)/(3·ln(2)) = 1/3.

   For at bestemme b skal man løse ligningen f(3) = 12 med hensyn til b, dvs. man skal løse:

   b·(1/3)³ = 12 ⇔

   b = 12·3³ = 12·27 = 324

   Dvs. f(x) = 324·(1/3)^x

   324·(1/3)¹¹ = 0,001829

Svar på opgave 5:

1. Grafen for f skærer x-aksen i x = 0 og x = 1, det må antages af fremgå af tegningen, men kan også vises ved at finde rødderne for f.

   En stamfunktion F(x) til f er F(x) = -(6/3)x³ + (6/2)x² = -2x³ + 3x².

   Arealet af M kan beregnes som integralet under grafen for f fra x = 0 til x = 1. Dette er lig med F(1) - F(0) = -2·1³ + 3·1² - ((-2)·0³ + 3·0²) = -2 + 3 - 0 = 1

   (Man kan også bruge: arealet af en parabel er to tredjedele grundlinje gange højde. Her er grundlinjen 1, mens højden findes for x = 1/2, der ligger midt mellem x = 0 og x = 1. Højde = -6·(1/2)² + 6·(1/2) = 3/2. Dvs. arealet er (2/3)·1·(3/2) = 1)

Svar på opgave 6:

1. f´(x) = 1/x - 1/2

   For at bestemme monotoniforholdene skal man lave en fortegnsundersøgelse af f´(x). Dette gøres ved:

   1/x - 1/2 = 0 ⇔ x = 2 (løs: f´(x) = 0 med hensyn til x)

   f´(1) = 1/1 - 1/2 = 1/2 (fortegn før nulpunkt er positivt)

   f´(3) = 1/3 - 1/2 = -1/6 (fortegn efter nulpunkt er negativt)

   Dvs. monotoniforholdene for f er: f er voksende for x < 2 og aftagende for x > 2

Svar på opgave 7:

1. Man skal finde y(10) som er: −10 + 21,8 = 11,8.

   Dvs. længdeforøgelsen pr. år af en ørred på 10 år er 11,8 cm/år

2. Man skal løse ligningen y(x) = 0 med hensyn til x. Man får:

   −x + 21,8 = 0 ⇔ x = 21,8.

   x er 21,8 år. Det er den alder, hvor ørreden holder op med at vokse.

Svar på opgave 8:

1. Man skal finde det positive nulpunkt for f(x). Dette gøres ved kommandoerne:

   f(x):=−0.05*x²+0.8*x+2.3 ▸ Udført og

   solve(f(x)=0,x)|x>0 ▸ x=18.4881

   Dvs. længden af stødet er 18,5 m

2. Den maksimale højde findes ved hjælp af kommandoerne:

   fMax(f(x),x) ▸ x=8. og

   f(8) ▸ 5.5

   Dvs. kuglens største højde er 5,5 m

Svar på opgave 9:

1. Man opretter to lister med henholdsvis højde og rumfang:

   højde:={5,10,15,20,25,30} ▸ {5,10,15,20,25,30}

   rumfang:={20,157,530,1256,2453,4239} ▸ {20,157,530,1256,2453,4239}

   Dernæst laver man en potensregression på listerne:

   PowerReg højde,rumfang,1: CopyVar stat.RegEqn,f1: stat.results ▸

   [["Titel","Potensregression"]

   ["RegEqn","a*x^b"]

   ["a",0.161587]

   ["b",2.99053]

   ["r²",0.999995]

   ["r",0.999997]

   ["Resid","{...}"]

   ["ResidTrans","{...}"]]

   Af resultattabellen ses, at a = 2,99053 og b = 0,161587 (Ti-Nspire bruger a og b modsat opgaven.)

2. Man skal løse ligningen f(x) = 2000 med hensyn til x. Dette gøres ved hjælp af f1(x), der er oprettet i Ti-Nspire.

   solve(f1(x)=2000,x) ▸ x=23.3628

   Dvs. højden af karaflen er 23,4 cm

3. Man bruger formlen for procent-procent vækst: (1 + y) = (1 + x)^a. Her er (1 + x) = 1 + 10 % = 1,1. a = 2,991. Man skal finde y i procent:

   (1.1^2.99053-1)*100 ▸ 32.9799

   Dvs. rumfanget vokser med 33 %

Svar på opgave 10:

1. Man opretter C(t) og beregner C'(72):

   c(t):=((900000*(1.031)^t)/(t+38)) ▸ Udført

   derivative(c(t),t)|t=72 ▸ 1580.03

   Dvs. C'(72) = 1580 kg CO₂/person/år. Dette er det væksten i udslippet for en person i år 1950 + 72 = 2022.

Svar på opgave 11:

1. Nulhypotesen er, at børns rygevaner er uafhængige af deres forældres.

   Man opretter en matrix med de observerede værdier.

   obs:=[[35,33][23,46]] ▸ [[35,33][23,46]]

   Man udfører en chi-i-anden uafhængighedstest med en frihedsgrad på matricen obs:

   χ²2way obs: stat.results ▸

   [["Titel","χ²-uafhængighedstest"]

   ["χ²",4.61495]

   ["PVal",0.031694]

   ["df",1.]

   ["ExpMatrix","[...]"]

   ["CompMatrix","[...]"]]

   Af resultatlisten ovenfor ses, at PVal = 0,032 (p-værdien), som er mindre end 5 % (0,05) og dermed forkastes nul-hypotesen.

Svar på opgave 12:

1. Der gælder sinusrealtionen: sin(∠A)/2,7 = sin(60°)/2,4, som bruges til at finde vinkel A:

   solve(sin(a*1.°)/2.7=sin(60°)/2.4,a)|0<a<90 ▸ a=76.9767

   Dvs. ∠A = 77,0°

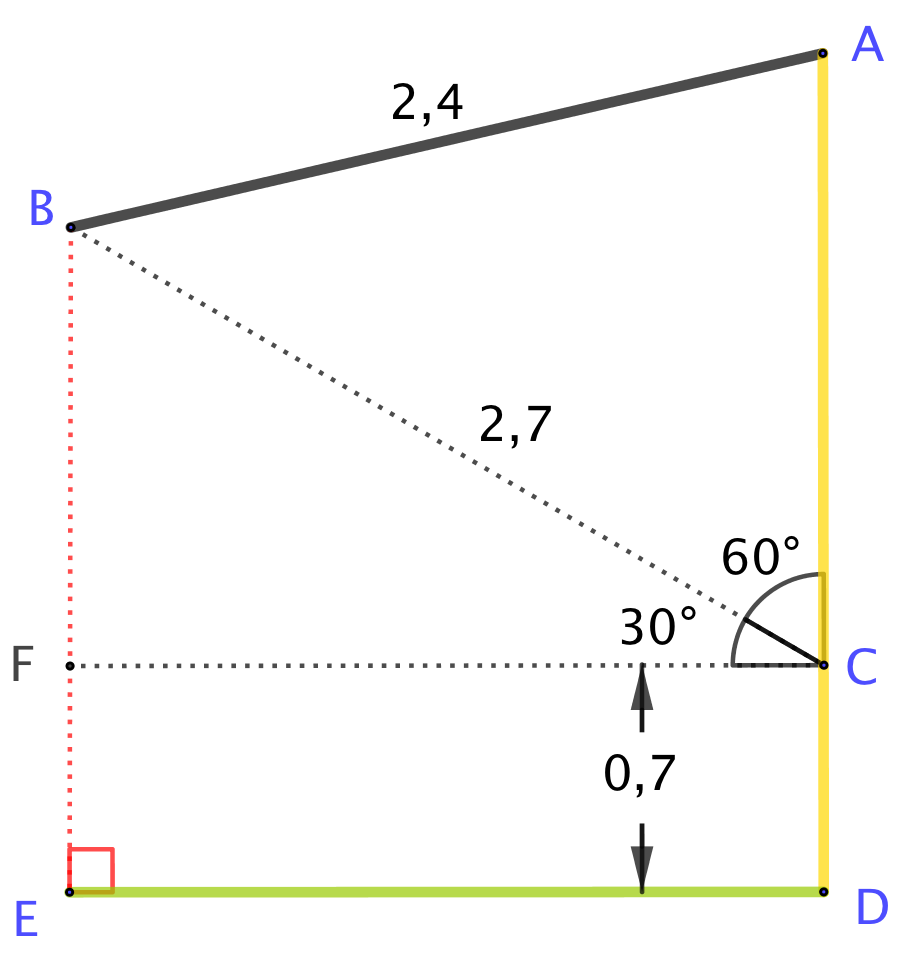
2. Det fremgår af nedenstående figur, at |EB| = |EF| + |FB| = |EF| + |BC|·sin(30°) = 0,7 + (2,7 m)·0,5 = 2,05 m

   

Svar på opgave 13:

1. Hældningen til en tangent gennem et punkt på grafen for f er lig med f´(x), hvor x er lig med førstekoordinaten til punktet.

   Man opretter f(x) i Ti-Nspire:

   f(x):=−x³+3*x²+x+4 ▸ Udført

   Man skal finde det x, hvor f´(x) = 4:

   solve(derivative(f(x),x)=4,x) ▸ x=1

   Dvs. førstekoordinaten for t's røringspunkt med f er x = 1

Svar på opgave 14:

1. Det fremgår af figuren i opgaven at h og x er kateter i en retvinklet trekant, hvor hypotenusen er 90. Dermed er sammenhængen mellem x og h givet ved hjælp af Pythagoras læresætning. Man får:

   x² + h² = 90² ⇔

   h² = 90² - x² ⇒

   h = √[90² - x²]

   Legemadrassen er et prisme med trekantet grundflade. Dens rumfang er derfor: længde gange grundflade =

   200·(1/2)·h·(2·x) =

   200·(1/2)·(√[90² - x²])·(2·x) =

   200·x·(√[90² - x²])

2. For at finde det x, der giver det største rumfang, opretter man R(x) i Ti-Nspire:

   r(x):=200*x*sqrt(90²-x²) ▸ Udført

   Dernæst finder man x-værdien ved hjælp af fMax kommandoen.

   fMax(r(x),x)*1. ▸ x=63.6396

   (Betingelsen 0<x<90 kunne evt. medtages sådan: fMax(r(x)*1.,x)|0<x<90 ▸ x=63.6396)

   Dvs. den x-værdi, der giver det højeste rumfang er x = 63,6