Svar på opgave 1:

1. A har negativ hældning, hvilket passer med f, hvor koefficienten til x er negativ.

   B går gennem y-aksen i en værdi, der er større end 1, hvilket stemmer med h, der har konstantleddet 2.

   C går gennem (0,0), det stemmer med g, der ikke har noget konstantled.

Svar på opgave 2:

1. Ligningen kan skrives: 1·x² + 8·x + 15 = 0

   Diskriminanten er D = 8² - 4·1·15 = 64 - 60 = 4

   Løsningen er x = -8/2 ± (1/2)·√4 ⇔

   x = -8/2 ± (1/2)·2 ⇔

   x = -4 ± 1 ⇔

   x = −5 eller x = −3

Svar på opgave 3:

1. Trekant ABD er retvinklet med AB som hypotenusen. |AB| kan findes ved hjælp af Pythagoras læresætning:

   |AB| = √(8²+6²) = 10

   Arealet af trekant ABC er 0,5·|AC|·6. Man ved, at omkredsen er 30, dvs. |AC| + |AB| + |BC| = 30 ⇒ |AC| + 10 + 7,5 = 30 ⇒ |AC| = 30 - (10 + 7,5) ⇒ |AC| = 12,5.

   Dermed er arealet af ABC = 0,5·12,5·6 = 37,5

Svar på opgave 4:

1. At fordoblingskonstanten er 3 betyder, at f(x) fordobles hver gang, at man lægger 3 til x.

   

Svar på opgave 5:

1. Tangenten til f(x) i x = 0 har formlen: y = f´(0)·x + f(0).

   f´(x) = 2·e^x, dvs. f´(0) = 2·e⁰ = 2.

   f(0) = 2·e^x + 1 = 3.

   Dvs. tangentens ligning er y = 2x + 3

Svar på opgave 6:

1. En stamfunktion til f har formen: 2x² + 3x + k.

   Den stamfunktion, der går igennem (1,10), skal opfylde ligningen: 2·1² + 3·1 + k = 10 => 5 + k = 10 => k = 5.

   Dvs. at stamfunktionen er F₁

Svar på opgave 7:

1. Man opretter lister med år efter 2005 og solcellekapaciteten.

   år:={2005,2006,2007,2008,2009,2010}-2005 ▸ {0,1,2,3,4,5}

   kapacitet:={2056,2899,4170,6120,9914,17320} ▸ {2056,2899,4170,6120,9914,17320}

   ExpReg år,kapacitet,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",1902.33]["b",1.52317]
   ["r²",0.990379]
   ["r",0.995178]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   a = 1,523 og b = 1902

2. Man skal finde S(2015-2005) = S(10). Man benytter den regressionsfunktion som Ti-Nspire har opretter. Den hedder f1(x). Man får:

   f1(2015-2005) ▸ 127874

   Dvs. solcellekapaciteten i 2015 er 127874 MW = 127,9 GW

3. Konstanten a er fremskrivningsfaktor, dvs. det tal som sidste års solcellekapacitet skal ganges med for at finde det nye års.

   Konstanten b er startværdi, dvs. solcellekapaciteten i 2005 målt i MW.

Svar på opgave 8:

1. BC er hypotenuse i den retvinklede trekant BCD. |BC| findes ved hjælp af Pythagoras læresætning:

   sqrt((6.)²+(2+5)²) ▸ 9.2195

   Dvs. |BC| = 9,22

   Arealet af trekant ABC er 0,5·|CD|·|AB| = 0,5·6·5 = 15

2. ∠B findes ved hjælp af en følgende trigonometriske ligning for retvinklede trekanter: modstående katete til vinkel v = hypotenuse·sin(v). Man får:

   solve(9.21954*sin(b*1.°)=6,b)|0<b<90 ▸ b=40.6013

   Dvs. ∠B = 40,6°

   For at beregne medianen m_a betragter man trekanten ABE som vist nedenunder.

   

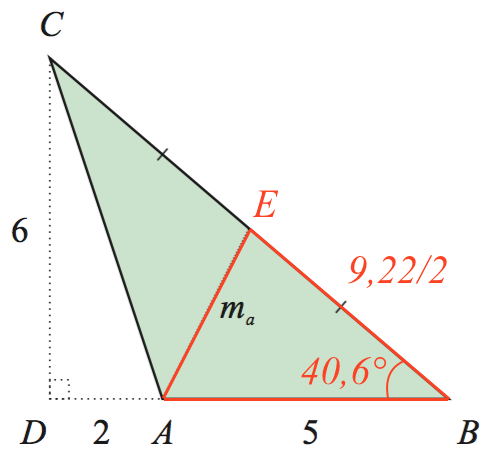
   Herudfra findes m_a ved hjælp af en cosinusrelation:

   solve(cos(40.6013°)=((9.21954/2)²+5²-ma²)/(2*(9.21954/2)*5),ma)|ma>0 ▸ ma=3.3541

   Dvs m_a = 3,35

Svar på opgave 9:

1. Man skal finde r, når V(r) = 40. Dette gøres ved at oprette V(r) i Ti-Nspire og løse ligningen V(r) = 40 med hensyn til r.

   v(r):=0.006*r^2.6657 ▸ Udført

   solve(v(r)=40,r) ▸ r=27.1948

   Dvs. græskarets radius er 27,2 cm

2. Man bruger formlen for procent-procent vækst for potensfunktioner: (1 + r_y) = (1 + r_x)^a. Her er r_y vækstraten for vægten og r_x der er vækstraten for radius. Det giver med hensyn til r_y:

   (1.1^2.6657-1)*100 ▸ 28.926

   Dvs. vækstraten for vægten af græskaret er 28,9 %

Svar på opgave 10:

1. Man starter med at oprette f(x) i Ti-NSpire:

   f(x):=x⁴-2*x²+4 ▸ Udført

   Dernæst løser man ligningen f´(x) = 0:

   solve(derivative(f(x),x)=0,x) ▸ x=−1 or x=0 or x=1

   Det ses, at løsningerne for ligningen f´(x) = 0 er: x = −1, x = 0 eller x = 1

2. Man laver en fortegnsundersøgelse af f´ som foretaget nedenunder.

   derivative(f(x),x)|x=−2 ▸ −24

   derivative(f(x),x)|x=−0.5 ▸ 1.5

   derivative(f(x),x)|x=0.5 ▸ −1.5

   derivative(f(x),x)|x=1.5 ▸ 7.5

   Fortegnsundersøgelsen viser, at f´(x) er negativ for x < -1, positiv for -1 < x < 0, negativ for 0 < x < 1 og positiv for x > 1. Dvs. monotoniforholdene for f er:

   f er aftagende for x < -1, voksende for -1 < x < 0, aftagende for 0 < x < 1 og voksende for x > 1

3. Man opretter g(x) i Ti-Nspire:

   g(x):=x²+2 ▸ Udført

   Nedenfor er graferne for g (rød) og f (blå) tegnet.

   

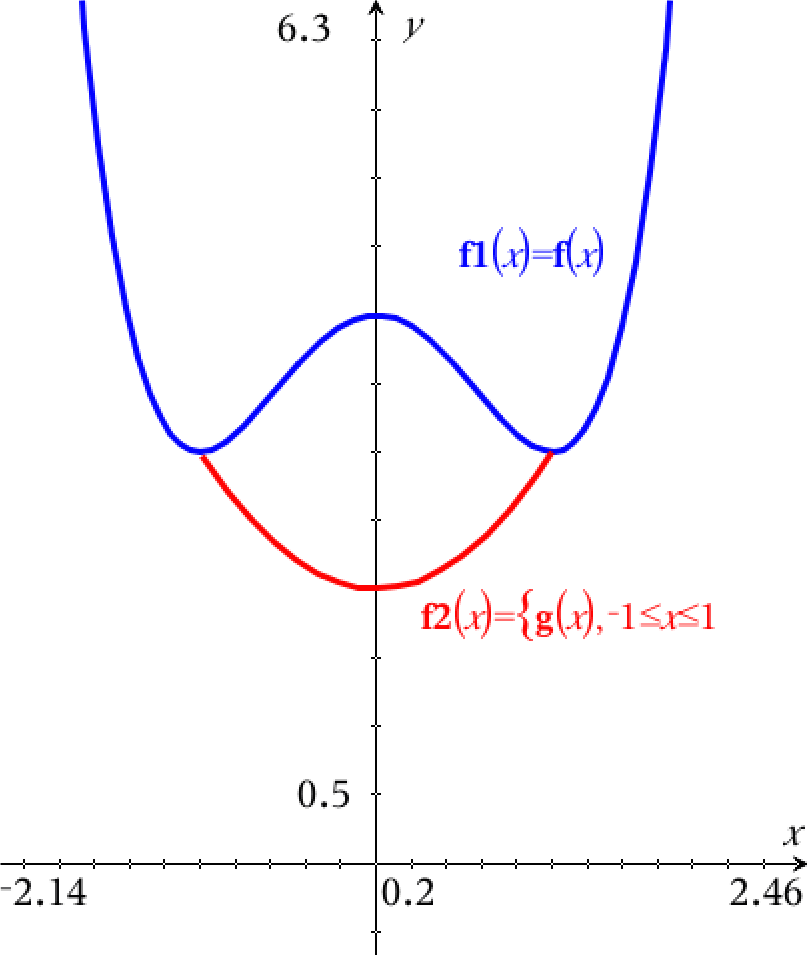
   Arealet af mellemrummet mellem kurverne er integralet af f-g fra x=-1 til x=1. Dette beregnes i Ti-Nspire:

   integral(f(x)-g(x),x,−1,1) ▸ 12/5

   Dvs. arealet er 12/5 eller 2,4

Svar på opgave 11:

1. Man opretter lister med stemmefordelingen for valget (stemmeandel) og den observerede stemmefordeling fra undersøgelsen (observeret).

   stemmeandel:={0.248,0.095,0.049,0.092,0.05,0.008,0.123,0.268,0.067} ▸ {0.248,0.095,0.049,0.092,0.05,0.008,0.123,0.268,0.067}

   observeret:={265,115,44,85,55,7,136,313,76} ▸ {265,115,44,85,55,7,136,313,76}

   Den forventede stemmefordeling fra undersøgelsen (forventet), hvis den følger fordelingen fra valget beregnes. Den er stemmefordelingen fra valget i procent gange antallet af personer, der blev spurgt i undersøgelsen.

   forventet:=stemmeandel*sum(observeret) ▸ {271.808,104.12,53.704,100.832,54.8,8.768,134.808,293.728,73.432}

   Man laver en Chi-i-anden goodness-of-fit test med 8 frihedsgrader på de to lister observeret og forventet

   χ²GOF observeret,forventet,8: stat.results ▸
    [["Titel","χ²-Goodness of Fit test"]
    ["χ²",7.26877]
    ["PVal",0.507932]
    ["df",8.]
    ["CompList","{...}"]]

   Det ses at PVal er 0,51, som er større end 5% (=0,05) og dermed accepteres nul-hypotesen.

Svar på opgave 12:

1. Omkredsen af metalstyket er to gange h plus omkredsen af en cirkel med radius r. Stykkets omkreds er 6, dvs. man får ligningen: 2h + 2πr = 6. Denne ligning løses med hensyn til h:

   solve(2*h+2*π*r=6,h) ▸ h=3-π*r

   Dvs. h udtrykt ved r er h = 3 - π·r

   Arealet af metalstykket er arealet af et rektangel med siderne h og r minus arealet af en cirkel med radius r. Man indsætter udtrykket for h som funktion af r og får:

   h·r - π·r² = (3 - π·r)·2r - π·r² = 6r - 3π·r²

2. a(r):=6*r-3*π*r² ▸ Udført

   Man laver en fortegnsundersøgelse for den afledede arealfuntion A'(r).

   solve(derivative(a(r),r)=0.,r) ▸ r=1/π

   derivative(a(r),r)|r=0 ▸ 6

   derivative(a(r),r)|r=1. ▸ −12.85

   Dette viser, at r = 1/π = 0,318 er lokalt maksimum.

   Nu skal man undersøge, om det er globalt minimum. For at gøre dette skal man finde grænserne for r:

   Der gælder: r > 0 og 2·r < h, da metalstykket ellers ville gå midt over. Da h er lig med 3 - π·r, får man den øvre grænse ud fra uligheden: 2·r < 3 - π·r ⇔ (2 + π)·r < 3 ⇔ r < 3/(2 + π) = 0,5835

   Man undersøger arealet i grænserne r = 0 og r = 0,5835 samt i det lokale maksimum i r = 0.3183:

   a(0) ▸ 0

   a(0.583477) ▸ 0.29224

   a(0.31831) ▸ 0.95493

   Det ses, at r = 1/π er globalt maksimum

   (Man kan også bruge Ti-NSpire kommandoen fMax(): fMax(a(r),r) ▸ r=1/π)