Svar på opgave 1:

1. 2·(3·x - 1) = 4·x + 8 ⇔

   3·x - 1 = (4/2)·x + 8/2 ⇔

   3·x - 2x = 4 + 1 ⇔

   x = 5

Svar på opgave 2:

1. Man har forskriften: y = 5,5x + 110.

   110 er gennemsnitshøjden for en 5-årig dreng (det ses ved at sætte x lig med nul).

   5,5 er det antal cm som en dreng vokser om året i gennemsnit, når han er mellem 5 og 17 år

Svar på opgave 3:

1. x² + x - 12 = 0 ⇔

   x = -1/2 ± (1/2)·√[1 + 4·12] ⇔

   x = -1/2 ± (1/2)·√49 ⇔

   x = -1/2 ± (1/2)·7 ⇔

   x = -1/2 - 7/2 ∨ x = -1/2 + 7/2 ⇔

   x = -8/2 ∨ x = 6/2 ⇔

   x = -4 ∨ x = 3

Svar på opgave 4:

1. f(x) = x³ + 4x² - 2x - 1

   Tangentens ligning i punktet (2,f(2)) er y = f´(2)·(x - 2) + f(2).

   f´(x) = 3x² + 8x - 2. Dermed er f´(2) = 3·2² + 8·2 - 2 = 26.

   f(2) = 2³ + 4·2² - 2·2 - 1 = 8 + 16 - 4 - 1 = 19.

   Det giver ligningen y = 26·(x - 2) + 19 ⇔ y = 26x - 33

Svar på opgave 5:

1. A er aftagende og skærer den positive del af y-aksen, hvilket svarer til g(x), der er en eksponentialfunktion, hvor 0<a<1 (2^-x = 2^-1·x = (2^-1)^x = (1/2)^x).

   B er en parabel (buet med et toppunkt og symmetrisk om y-aksen), der svarer til h(x), der er et andengradspolynomium.

   C er voksende og skærer den positive del af y-aksen, hvilket svarer til f(x), der er en eksponentialfunktion, hvor a>1.

Svar på opgave 6:

1. f(x) = 5x⁴ + e^x.

   En vilkårlig stamfunktion til f har formen: e^x + x⁵ + k, hvor k er en konstant.

   Man skal finde k, så e⁰ + 0⁵ + k = 10 ⇔ k = 9.

   Dvs. den søgte stamfinktion er F(x) = e^x + x⁵ + 9

Svar på opgave 7:

1. Man opretter lister med antal år efter 1999 og udgifter.

   antal_år:={1999,2000,2001,2002,2003,2004,2005,2006,2007,2008,2009}-1999 ▸ {0,1,2,3,4,5,6,7,8,9,10}

   udgift:={1.44,1.56,16.4,1.82,2.04,2.17,2.43,2.62,2.85,3.3,3.49} ▸ {1.44,1.56,16.4,1.82,2.04,2.17,2.43,2.62,2.85,3.3,3.49}

   Man laver en eksponentiel regression på de to lister i Ti-Nspire.

   ExpReg antal_år,udgift,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",2.37109]
   ["b",1.02837]
   ["r²",0.019775]
   ["r",0.140624]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Det ses at a = 1,0284 og b = 2,371 (Ti-Nspire bruger a og b modsat opgaven).

2. Fordoblingskonstanten er ln(2)/ln(a) år = ln(2)/ln(1,0284) år = 24,8 år

3. Man skal finde den den procentvise forskel mellem 2,61 og y(2010-1999) = y(11) = 2,371·1,0284¹¹ = 3,23.

   Man får den procentvise forskel: (3,23-2,61)/2,61)·100 % = 23,6 %

Svar på opgave 8:

1. |AC| findes ved hjælp af en cosinusrelation:

   solve(cos(113.°)=(6.19²+10.3²-ac²)/(2*6.19*10.3),ac)|ac>0 ▸ ac=13.9366

   Man får at |AC| = 13,9

   Vinkel A findes også ved hjælp af en cosinusrelation:

   solve(cos(a*1.°)=(6.19²+13.9366²-10.3²)/(2*6.19*13.9366),a)|0<a<180 ▸ a=42.868

   Dvs. ∠A = 42,9°

2. Arealet af trekant ABE er 0,5·|AE|·højde, hvor højden er |AB|·sin(∠A) = 6,19·sin(42,9°) = 4,2111.

   Dvs. man skal finde |AE|, så 0,5·|AE|·4,2111 = 5. Dette gøres ved hjælp af solve-kommandoen:

   solve(0.5*ae*4.21113=5,ae) ▸ ae=2.37466

   Dvs. |AE| = 2,37

Svar på opgave 9:

1. Man skal løse de to sammenhørende ligninger: f(2) = 3 og f(4) = 7. Man starter med at oprette f(x) i Ti-Nspire med konstanterne a og b:

   f(x):=b*x^a ▸ Udført

   Dernæst løser man ligningerne med solve()-kommandoen:

   solve(f(2.)=3 and f(4)=7,a,b)|a>0 ▸ a=1.22239 and b=1.28571

   Dvs. f(x) = 1,286·x^1,222

Svar på opgave 10:

1. Man skal finde nulpunkterne for f(x).

   f(x):=x⁴+8*x³+18*x²+16*x+5 ▸ Udført

   solve(f(x)=0,x) ▸ x=−5 or x=−1

   Dvs. løsningen til f(x) = 0 er: x = −5 eller x = −1

2. f´(x) beregnes:

   derivative(f(x),x) ▸ 4*x³+24*x²+36*x+16

   Dvs. f´(x) = 4x³ + 24x² + 36x + 16

   For at finde monotoniforholdene for f(x), så laver man en fortegnsbestemmelse for f´(x). Man løser først f´(x) = 0.

   solve(derivative(f(x),x)=0,x) ▸ x=−4 or x=-1

   Man finder fortegn for f´ omkring disse værdier af x:

   derivative(f(x),x)|x=−5 ▸ −64

   derivative(f(x),x)|x=−3 ▸ 16

   derivative(f(x),x)|x=0 ▸ 16

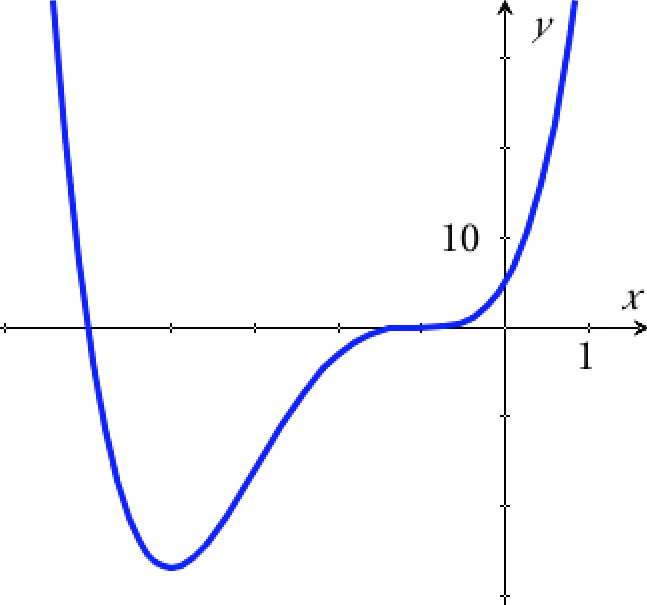
   Det ses at f er aftagende for x < -4 og voksende for x > -4.

   (Bemærk: f er ikke strengt voksende for x > -4, da f´(-1) = 0).

   Nedenunder er vist en graf for f:

   

Svar på opgave 11:

1. Man opretter funktionerne:

   f(x):=sqrt(x) ▸ Udført

   g(x):=0.5*x ▸ Udført

   Man finder skæringspunkterne ved at løse ligningen f(x) = g(x):

   solve(f(x)=g(x),x) ▸ x=0. or x=4.

   For at finde y-koordinaterne indsætter man disse x værdier i udtrykket for den ene funktion.

   Man får: f(0) ▸ 0 henholdsvis f(4) ▸ 2.

   Dvs. koordinatsættene for skæringspunkterne mellem graferne for f og g er (0,0) og (4,2)

2. Arealet af M er integralet af f(x) - g(x) fra x = 0 til x = 4:

   integral(f(x)-g(x),x,0,4) ▸ 1.33333

   Dvs. arealet af M er 1,333

Svar på opgave 12:

1. Man opretter en liste med fordelingen af blodtyper i hele befolkningen (den forventede fordeling):

   fordeling:={0.37,0.35,0.08,0.04,0.07,0.06,0.02,0.01} ▸ {0.37,0.35,0.08,0.04,0.07,0.06,0.02,0.01}

   Man opretter en liste med det observerede antal af hver blodtype:

   observeret:={350,320,80,55,56,50,30,9} ▸ {350,320,80,55,56,50,30,9}

   Man finder de forventede antal som summen af de observerede antal gange den forventede fordeling. Listen over de forventede antal blodtyper kaldes forventet:

   forventet:=fordeling*sum(observeret) ▸ {351.5,332.5,76.,38.,66.5,57.,19.,9.5}

   Dvs. de forventede antal er:

   Blodtype A+ : 351,5

   Blodtype O+ : 332,5

   Blodtype B+ : 76

   Blodtype AB+ : 38

   Blodtype A- : 66,5

   Blodtype O- : 57

   Blodtype B- : 19

   Blodtype AB- : 9,5

2. Man laver en chi-i-anden goodness-of-fit test med 7 frihedsgrader på de to lister med observeret og forventet antal antal:

   χ²GOF observeret,forventet,7: stat.results ▸
   [["Titel","χ²-Goodness of Fit test"]
   ["χ²",17.2044]
   ["PVal",0.016125]
   ["df",7.]
   ["CompList","{...}"]]

   Det ses, at p-værdien (PVal) er lig med 0,016 som er mindre end 5 % (0,05). Dermed forkastes nul-hypotesen.

Svar på opgave 13:

1. Den grønne firkants areal er arealet af det brune kvadrat minus arealet af de retvinklede trekanter mærket "I" og "II". Dette er vist nedenunder.

   

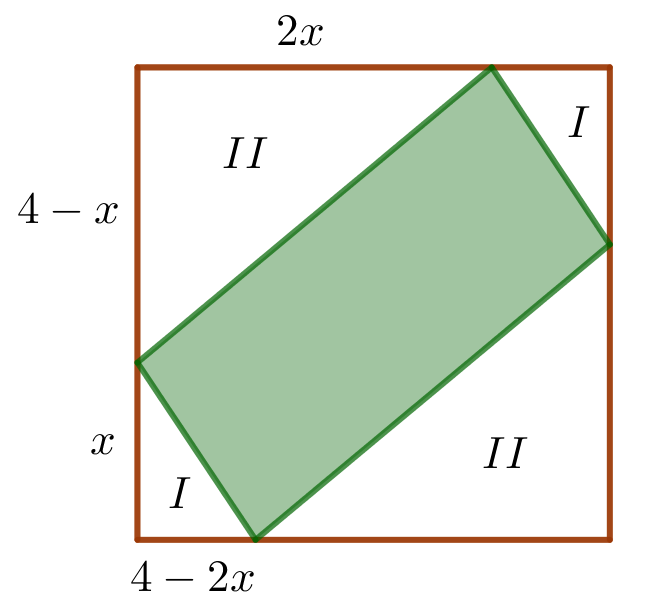
   Det brune kvadrats areal er 4² = 16.

   En trekant med mærket "I" har arealet 0,5·x·(4 - 2x). Tilsammen har de to trekanter mærket "I" arealet 2·0,5·x·(4 - 2x) = x·(4 - 2x).

   En trekant med mærket "II" har arealet 0,5·(2x)·(4 - x). Tilsammen har de to trekanter mærket "II" arealet 2·x·(4 - x).

   Den grønne firkants areal bliver derfor: 16 - x·(4 - 2x) - 2·x·(4 - x) = 16 - 4x + 2x² - 8·x + 2x² = 4x² - 12x + 16.

2. Man opretter arealfunktionen T(x):

   t(x):=4*x²-12*x+16 ▸ Udført

   For at finde mindsteværdien undersøger man værdien af T(x) dels i endepunkterne x = 0 og x = 2, dels for de x, hvor f´(x) = 0.

   (Man behøver ikke at lave en undersøgelse af om disse punkter er lokale minimums- eller maksimumspunkter, da det er nemmere, at bare indsætte de x-værdien, som man finder og se, hvilket der giver den mindste værdi af T(x).)

   Man starter med at løse f´(x) = 0:

   solve(derivative(t(x),x)=0,x) ▸ x=3/2

   Man indsætter nu den fundne x-værdi, sammen med x = 0 og x = 2 for at se, hvor arealet er mindst:

   t(3/2) ▸ 7

   t(0) ▸ 16

   t(2) ▸ 8

   Dette viser, at det mindste areal fås for x = 3/2 = 1,5

   (I Ti-Nspire kan man også bruge kommandoen: fMin(t(x),x)|0<x<2 ▸ x=3/2).

   Nedenunder er en interaktiv Geogebra tegning, der viser hvordan den grønne firkant og dens areal varierer med x. (x er her kaldet "k", da "x" er forbeholdt koordinater i Geogebra.)