Svar på opgave 1:
-
Man skal løse en førstegradsligning med en ubekendt.
2·((1/2)·x - 3) + 1 = 5·x - 2·(x + 1) ⇔
(2·(1/2)·x - 2·3) + 1 = 5·x - (2·x + 2·1) ⇔
(x - 6) + 1 = 5·x - (2·x + 2) ⇔
x - 6 + 1 = 5·x - 2·x - 2 ⇔
-2·x = 3 ⇔
x = -3/2
Svar på opgave 2:
-
Vektorerne a og b er ortogonale, når (og kun når) de er egentlige, og a·b = 0
Man får: a·b = 0 ⇒ (2,4)·(t,t+3) = 0 ⇔ 6·t + 12 = 0 ⇔ t = -2.
Dvs. vektorerne a og b er ortogonale, når t = -2
Svar på opgave 3:
-
For at finde monotoniforholdene for f(x) skal man lave en fortegns-undersøgelse af f '(x).
f '(x) = x2 + 2·x.
Man finder nulpunkterne for f '(x):
f '(x) = 0 ⇒ x2 + 2·x = 0 ⇔ x = −2 ∨ x = 0
Herefter findes fortegnene for f ' omkring nulpunkterne:
f '(-3) = 3 (f ' er positiv),
f '(-1) = -1 (f ' er negativ) og
f '(1) = 1 (f ' er positiv).
Dvs. f er voksende for x < -2, aftagende for -2 < x < 0 og voksende for x > 0
Svar på opgave 4:
-
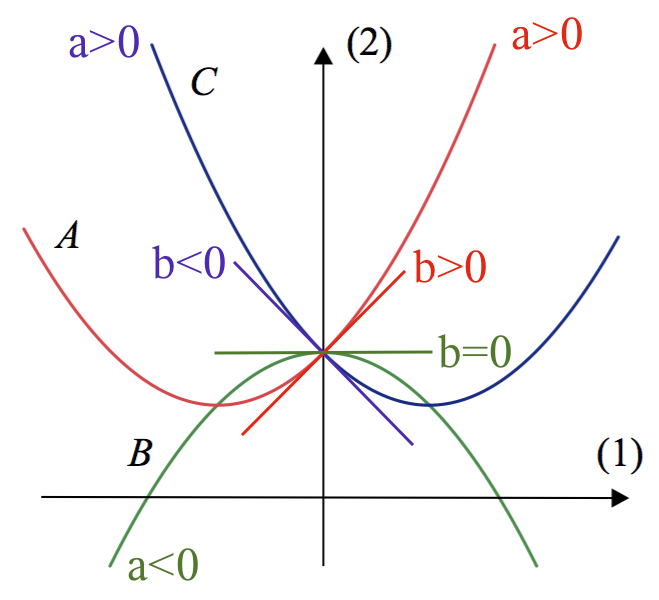
Koefficienten a viser, hvilken vej grenen i parablen vender. Positiv a: genene vender opad, negativ a: grenene vender nedad.
Koefficienten b viser tangentens hældning i parablens skæring med y-aksen.
Koefficienten c viser parablens skæring med y-aksen. Denne er ens for alle, og kan derfor ikke bruges til at skelne.
Man får:
A: a er positiv og b er positiv, A svarer til g
B: a er negativ og b er 0, dvs. B svarer til f
C: a er positiv og b er negativ, dvs. C svarer til h
Dette er vist på tegningen nedenunder:
Svar på opgave 5:
-
Trekanterne ΔABC, ΔBEF og ΔCDE er ensvinklede, som det også fremgår af tegningen:
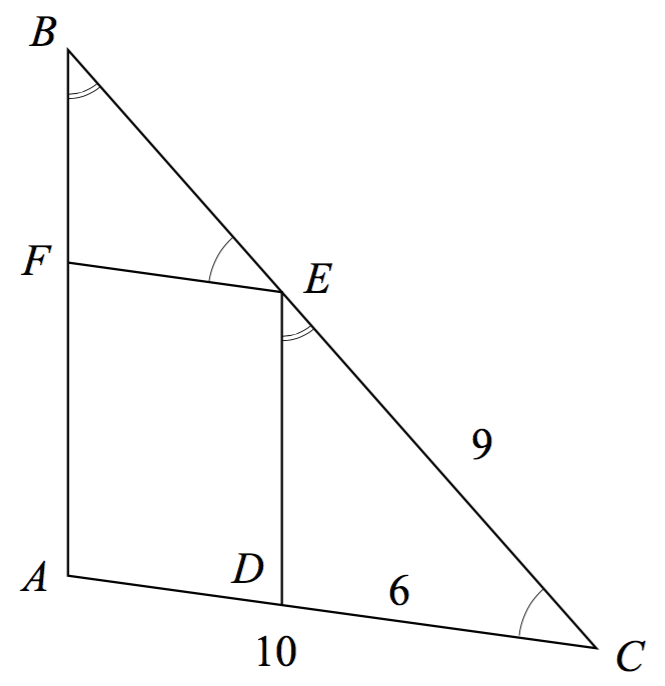
Det ses, at: |BC|/|AC| = |CE|/|CD| ⇒
(|BE|+9)/10 = 9/6 ⇔
|BE| = 10·9/6 - 9 = 6
Svar på opgave 6:
-
F(x) = (a/3)·x3 + x2 - 4x + k, hvor k er en reel konstant.
Man skal bestemme a og k, så F(0) = 4 og F(1) = 3. Man får:
(a/3)·03 + 02 - 4·0 + k = 4 ∧ (a/3)·13 + 12 - 4·1 + k = 3 ⇔
k = 4 ∧ a/3 + 1 - 4 + k = 3 ⇔
k = 4 ∧ a/3 = 2 ⇔
a=6 ∧ k=4
Dvs. stamfunktionen bliver: F(x) = 2x3 + x2 - 4x + 4
Svar på opgave 7:
-
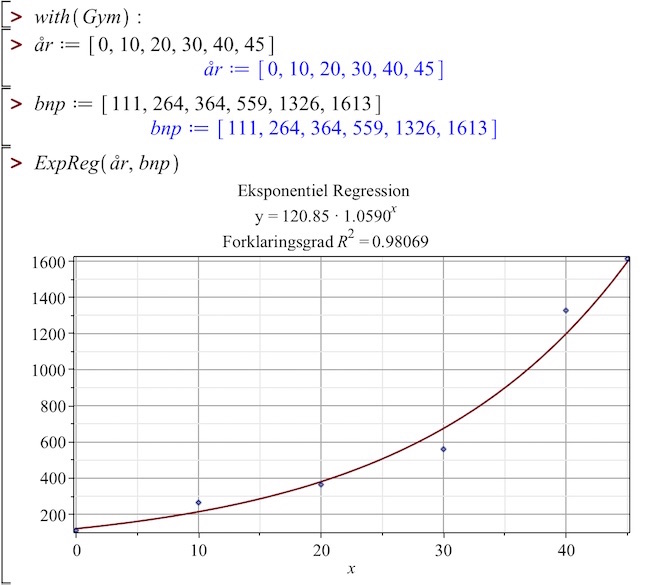
Man opretter lister med antal år efter 1970 (år) og BNP (bnp) i Ti-Nspire:
år:={1970,1980,1990,2000,2010,2015}-1970 ▸ {0,10,20,30,40,45}
bnp:={111,264,364,559,1326,1613} ▸ {111,264,364,559,1326,1613}
Ud fra dette laver man en eksponentiel regression:
ExpReg år,bnp,1: CopyVar stat.RegEqn,f1: stat.results ▸
[["Titel","Eksponentiel regression"]
["RegEqn","a*b^x"]
["a",120.847]
["b",1.05904]
["r²",0.980697]
["r",0.990302]
["Resid","{...}"]
["ResidTrans","{...}"]]Regressionsfunktionen i Ti-Nspire udskrives: f1(x) ▸ 120.847*(1.05904)x
(...navnet på funktionen fremgår af "ExpReg år,bnp,1: CopyVar stat.RegEqn,f1: stat.results".)Dvs. a = 1,059 og b = 120,8
-
Tallet a er fremskrivningsfaktoren
Fordoblingstiden er ln(2)/ln(a) = ln(2)/ln(1,059) år = 12,1 år
-
Man skal finde det x, der gør, at f1(x) = 2000. Man får:
solve(f1(x)=2000,x) ▸ x=48.9245
Hertil skal lægges 1970. Dvs. årstallet er: 1970 + 49 = 2019
Man runder op, for at få det første årstal, hvor BNP pr. indbygger er lig med eller over 2000.
Beregninger for opgave 7 a) i Maple:
Svar på opgave 8:
-
Cirklens ligning er (x-a)2 + (y-b)2 = r2, hvor (a,b) = (5,4) er koordinaterne for cirklens centrum, og r er dens radius.
Man skal finde r2. Denne er lig med CP2.
CP = (9 - 5,3 - 4) = (4,-1). Dermed gælder, at r2 = (4,-1)·(4,-1) = 17.
Dvs. cirklens ligning er: (x-5)2 + (y-4)2 = 17
-
Linjen indeholder P og har CP som normalvektor. (Tegning i Geogebra).
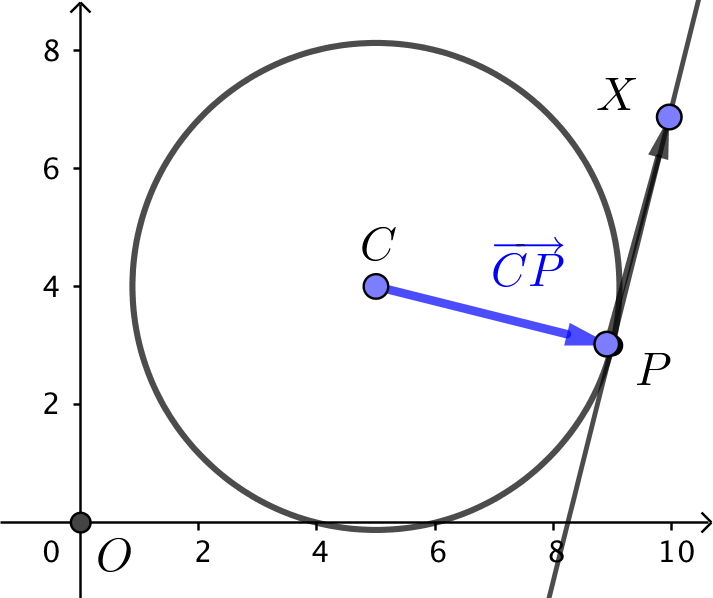
For et punkt X = (x,y) på linjen gælder: CP·PX = 0 ⇒
(4,-1)·(x - 9,y - 3) = 0 ⇔
4·(x - 9) + (-1)·(y - 3) = 0 ⇔
4x - 36 - y + 3 = 0 ⇔
4x - y - 33 = 0
Dvs. ligningen for tangenten gennem P er 4x - y - 33 = 0
-
Det andet tangentpunkt kaldes R. Det er placeret i den modsatte ende af diameteren gennem P.
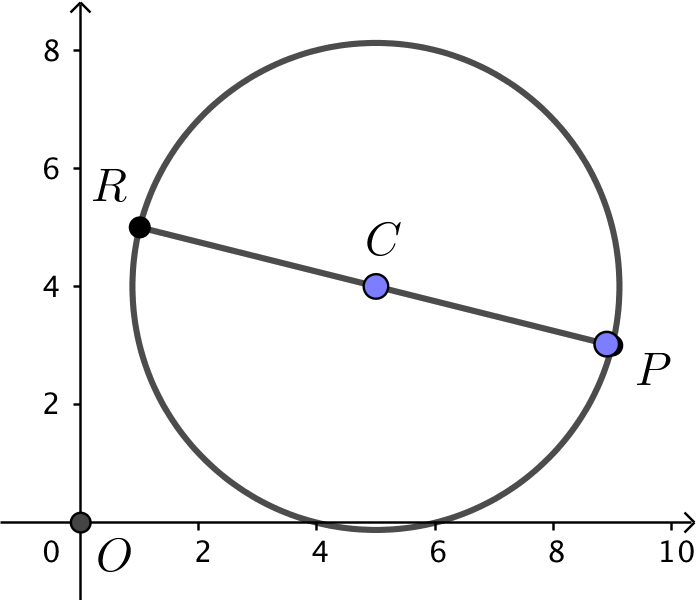
Man finder R's koordinater ved hjælp af R's stedvektor: OR = OC - CP = (5,4) - (4,-1) = (1,5).
Dvs. koordinaternene til den anden tangents røringspunkt er (1,5)
Svar på opgave 9:
-
Funktionen sin(0,0172x-1,5) ligger mellem -1 og 1 forudsat, at (0,0172x-1,5) ligger i et interval, der mindst har længden 2π.
Det antages, at 0 ≤ x ≤ 365. Dvs. at (0,0172x-1,5) ligger i et interval med længden 365·0,0172 ≈ 2π. Dermed har man:
Mindste værdi: (−1)·15 + 8 = −7 .
Største værdi: 15 + 8 = 23
Svar på opgave 10:
-
Nulhypotese: Læsehastigheden har ikke ændret sig
-
Man laver en Chi-i-anden goodness of fit-test. Antal frihedsgrader er 4.
Man opretter lister med det observerede antal elever (observeret) og det forventede antal elever (forventet) i Ti-Nspire:
observeret:={9,41,62,26,12} ▸ {9,41,62,26,12}
forventet:={9.2%,31.%,41.3%,15.1%,3.4%}*150 ▸ {13.8,46.5,61.95,22.65,5.1}
Teststørrelse: sum((observeret-forventet)2/forventet) ▸ 12.1509
Kritisk værdi: invχ²(1-5%,4) ▸ 9.48773
Nulhypotesen forkastes, fordi teststørrelse er større end den kritiske værdi.
Beregninger for opgave 10 b) i Maple:
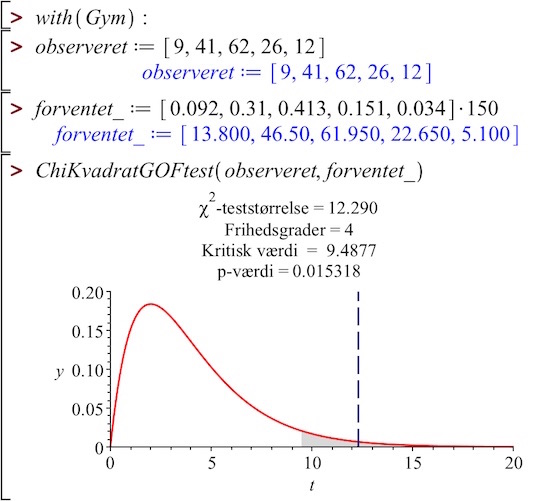
Bemærk at forventet_ er anvendt, idet forventet er et reserveret ord i gympakken.
Svar på opgave 11:
-
Man opretter funktionen i Ti-Nspire:
n(t):=20414/(1+6.325*exp(−0.378*t))+54349 ▸ Udført
Man skal beregne N(t) for t = 2020-2014 = 6
n(6) ▸ 66685.5
Dvs. antallet af fødsler i 2020 er 66686
-
Man beregner N'(4) i Ti-Nspire:
derivative(n(t),t)|t=4 ▸ 1876.77
Dvs. N'(4) = 1877
Tallet er stigningen i antal årlige fødsler i 2018.
Beregninger for opgave 11 i Maple:
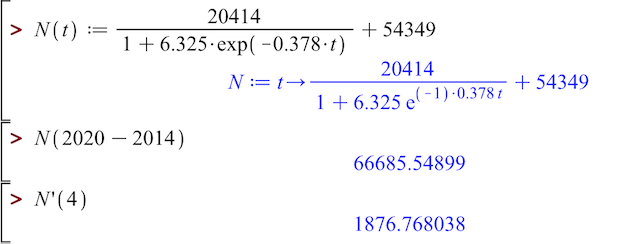
Svar på opgave 12:
-
Funktionen f(x) oprettes i Ti-Nspire:
f(x):=−x2+4*x ▸ Udført
Arealet af M er integralet af M mellem nulpunkterne for f. Nulpunkterne beregnes:
solve(f(x)=0,x) ▸ x=0 or x=4
Dvs. arealet af M er integralet af f fra x = 0 til x = 4. Man får:
integral(f(x),x,0,4) ▸ 32/3
Dvs. arealet af M er 32/3 = 10,67
-
Man opretter g(x) i Ti-Nspire:
g(x):=k*x ▸ Udført
For at beregne arealet af M1 og M2 skal man kende skæringspunkterne for f og g. Disse skæringspunkter beregnes:
solve(f(x)=g(x),x) ▸ x=−(k-4) or x=0
Dvs. skæringspunktet, der ligger mellem x = 0 og x = 4, er x = 4-k. Dette er tegnet nedenfor:
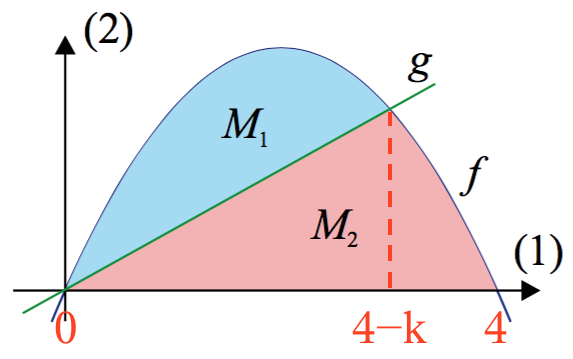
Dermed bliver arealet af M1 integralet af f-g mellem x = 0 og x = 4-k.
Arealet af M2 er integralet af g fra x = 0 til x = 4-k lagt sammen med integralet af f fra x = 4-k til x = 4.
integral(f(x)-g(x),x,0,4-k) ▸ −(k-4)3/6 (areal af M1)
integral(g(x),x,0,4-k)+integral(f(x),x,4-k,4) ▸ k*(k2-12*k+48)/6 (areal af M2)
Man finder det k, der gør, at de to arealer er lige store:
solve(−(k-4)3/6=k*(k2-12*k+48)/6.,k) ▸ k=0.825198
Dvs. k = 0,825
(Evt.: arealet af M1 = halvdelen af arealet af M, hvilket giver: solve(−(k-4)3/6=0.5*32/3,k) ▸ k=0.8252)
Beregninger for opgave 12 i Maple:
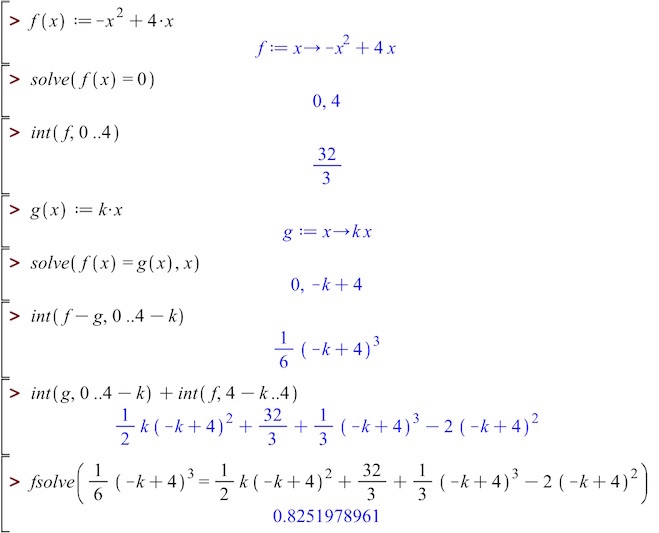
Svar på opgave 13:
-
Linjen har planens normalvektor som retningsvektor. Planens normalvektor aflæses af dens ligning:
2·x + (-2)·y + 1·z - 30 = 0
Dvs. planens normalvektor og dermed linjens retningvektor er n = (2,-2,1).
Linjen går igennem kuglens centrum, som aflæses af kuglens ligning:
(x - 3)2 + (y - (-4))2 + (z - 2)2 = 9
Dvs. kuglens centrum, C, er (3,-4,2).
Linjens parameterfremstilling kan derfor skrives: (x,y,z) = (3+2·t,−4-2·t,2+t).
Man indsætter x(t) = 3+2t, y(t) = −4−2t og z(t) = 2+t i kuglens ligning og løser ligningen med hensyn til t:
(3+2t−3)2 + (−4−2t+4)2 + (2+t−2)2 = 9 ⇔ 9t2 = 9 ⇔ t = ±1
Dvs. linjen skærer kuglen for parameterværdierne t=−1 og t=1. Disse t-værdier indsættes i linjens parameterfremstilling for at finde punkternes koordinater:
t=−1: (3+2·(−1),−4-2·(−1),2+(−1)) = (1,−2,1)
t=1: (3+2·(1),−4−2·(1),2+(1)) = (5,−6,3)
Dvs. linjens skæringspunkter med kuglen er (x,y,z) = (1,−2,1) og (x,y,z) = (5,−6,3)
-
Afstanden mellem plan og kugle kan beregnes som afstanden mellem planen og kuglens centrum minus kuglens radius.
Afstanden mellem planen og kuglens centrum er:
dist(C,α) = |2·3+(-2)·(-4)+1·2-30|/√[22+(-2)2+12] = |-14|/√9 = 14/3.
Afstanden mellem planen α og kuglen bliver dermed: 14/3 - 3 = 5/3
Skitseret løsning af opgave 13 i Geogebra:
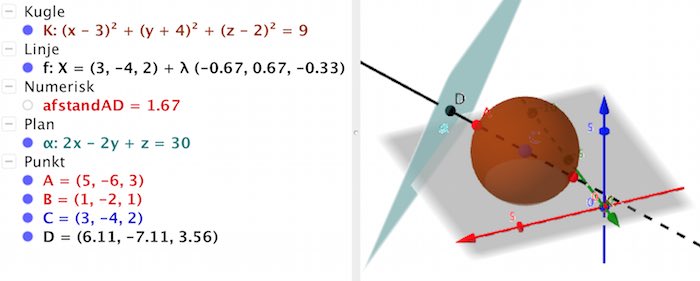
Løsningen er her tænkt som en kontrol, men man må gerne løse hele opgaven i Geogebra, blot man forklarer, hvad man gør.
Svar på opgave 14: Kaffebæger
-
Funktionen f er voksende og lineær og går gennem punkterne (x,y) = (0,3) og (x,y) = (11,5). Dette er vist nedenunder:
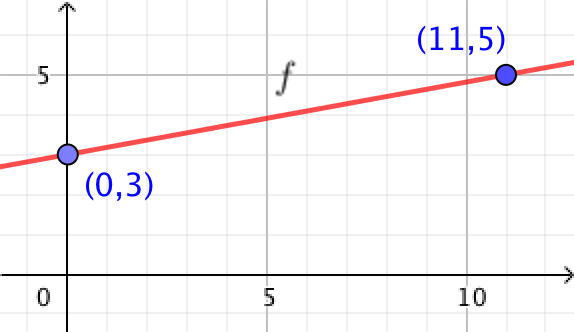
Forskriften er f(x) = a·x + b, hvor a er linjens hældning og b er værdien ved skæring med y-aksen.
Man får: a = (5 - 3)/11 = 2/11 og b = 3.
Dvs. forskriften for f er f(x) = (2/11)·x + 3
-
Man bruger rumfangsformlen for en keglestub: V = (1/3)·π·h·((r1)2 + (r2)2 + r1·r2), hvor V er keglestubbens rumfang, h er højden, r1 er den lille radius og r2 er den store radius.
Her er h = 8, r1 = 3 og r2 = f(8) = (2/11)·8 + 3 = 4,4546.
Man får derfor rumfanget: (1/3)·π·8·(32 + 4,45462 + 3·4,4546) = 353,6
Dvs. volumenet af kaffe i bægeret er 353,6 cm3
Svar på opgave 15:
-
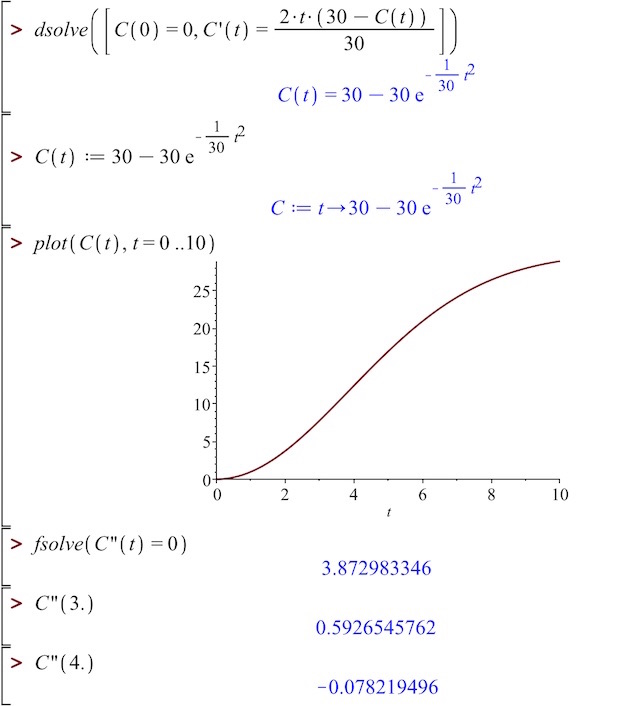
Man løser differentialligningen i Ti-Nspire:
deSolve(c'=2*t*(30-c)/30 and c(0)=0,t,c) ▸ c=30-30*exp(−t2/30)
Dvs. løsningen er C(t) = 30·(1−exp(−t2/30))
-
Man starter med at oprette funktionen C(t) i Ti-Nspire:
c(t):=30-30*exp(−t2/30) ▸ Udført
Man skal finde størsteværdien for C'(t) for 0<t<10. For at gøre dette, skal man løse ligningen C''(t) = 0:
solve(derivative(c(t),t,2)=0. and 0<t<10,t) ▸ t=3.87298
Man skal undersøge, om dette er et maksimum og finder derfor C'(3) og C'(4):
derivative(c(t),t,2)|t=3. ▸ 0.592655 (C'(t) vokser før t=3,873)
derivative(c(t),t,2)|t=4. ▸ −0.078219 (C'(t) aftager efter t=3,873)
Dvs. C'(3,873) er et maksimum, og derfor er 3,9 døgn efter start det tidspunkt, hvor koncentrationen af stoffet vokser hurtigst.
Beregninger for opgave 15 i Maple: