Svar på opgave 1:

1. Man bruger standard-løsningsmetoden for en andengradsligning:

   x = (−b + √D)/(2·a)

   Her er: a = -2, b = 2 og c = 12. Diskriminanten, D = 2² - 4·(−2)·12 = 100 ⇒ √D = √100 = 10.

   Man får:

   x = (−2±10)/(2·(−2)) ⇔

   x = −2 ∨ x = 3

Svar på opgave 2:

1. Skaleringsfaktoren er |AB|/|AD| = 10/5 = 2.

   Man finder |BC| ved hjælp af Pythagoras læresætning for en retvinklet trekant.

   |AC|² + |BC|² = |AB|² ⇔

   |BC|² = |AB|² - |AC|² ⇒

   |BC|² = 10² - 8² ⇔

   |BC|² = 36 ⇔

   |BC| = √36 = 6

   |DE| = 0,5·|BC| = 0,5·6 = 3

Svar på opgave 3:

1. A er grafen for en eksponentiel funktion, hvor grundtallet ligger mellem 0 og 1 (en monotont aftagende funktion defineret for alle reelle tal, der har y = 0 som asymptote for x gående mod plus uendelig).

   B er grafen for en eksponentiel funktion, grundtallet er større end 1 (en monotont voksende funktion defineret for alle reelle tal, der har y = 0 som asymptote for x gående mod minus uendelig).

   C er grafen for en potensfunktion, hvor eksponenten ligger mellem 0 og 1 (en monotont voksende funktion defineret for alle positive reelle tal, og som har aftagende hældningskoefficient (uden vandret asymptote) for x gående mod uendelig).

   Dvs. A svarer til g(x), B svarer til f(x) og C svarer til h(x).

Svar på opgave 4:

1. Modellen er:

   f(x) = 70,4·(1-1,5%)^x = 70,4·0,985^x (0 ≤ x ≤ 25),

   hvor f(x) mio. tons CO₂, og x er antal år efter 1990.

Svar på opgave 5:

1. Man gør prøve:

   Venstre side: f'(x) = (1/3)·exp(x/3) - 1

   Højre side: (x + f(x))/3 = (x + exp(x/3) - x - 3)/3 = (1/3)·exp(x/3) - 1

   Dvs. prøven stemmer, og dermed er f(x) en løsning til differentialligningen.

Svar på opgave 6:

1. Man bruger integration ved substitution.

   Substitutionen er: y = ln(x) og dy = (1/x)·dx. Det giver:

   ∫(3·y²dy) = 3·(1/3)·y³ = y³ = (ln(x))³

   Hertil skal lægges en arbitrær konstant kaldet K, og man får, at integralet er

   (ln(x))³ + K

Svar på opgave 7:

1. Man opretter lister med data for afstand og lysintensitet:

   afstand:={1.,1.5,2.,2.5,3.,3.5} ▸ {1.,1.5,2.,2.5,3.,3.5}

   lysintensitet:={560,248,140,90,62,46} ▸ {560,248,140,90,62,46}

   Man laver en potensregression på listerne:

   PowerReg afstand,lysintensitet,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Potensregression"]
   ["RegEqn","a*x^b"]
   ["a",558.85]
   ["b",−1.99637]
   ["r²",0.999984]
   ["r",−0.999992]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Man ser at a = -1,996 og b = 558,9

   Det bemærkes, at Ti-Nspire bruger a og b modsat opgaven.

2. Man skal finde det x, der gør at regressionsfunktionen giver 5. Regressionsfunktionen hedder f1(x) i Ti-Nspire. Man får:

   solve(f1(x)=5,x) ▸ x=10.6176

   Dvs. afstanden til lyskilden skal være 10,62 m før lysintensiteten kommer ned på 5 W/m²

3. Man bruger formlen for procent-procent vækst for f(x).

   1.4^−1.996 - 1 ▸ −0.4891

   Dvs. lysintensiteten falder med 49 %, når man øger afstanden med 40 %.

Svar på opgave 8:

1. Linjen l har a som retningsvektor og tværvektoren til a som normalvektor. Tværvektoren til a er â = (5,2)

   Et punkt på l kaldes Q = (x,y). PQ = (x-1,y-3).

   Der gælder, at PQ·â = 0 ⇒

   (x-1,y-3)·(5,2) = 0 ⇔ (x-1)·5 + (y-3)·2 = 0 ⇔ 5x-5 + 2y-6 = 0 ⇔ 5x + 2y = 11

   Dvs. cirklens ligning er: (x-5)² + (y-4)² = 17

2. Man opretter vektorerne a og b i Ti-Nspire:

   a:=[2,−5] ▸ [2,−5]

   b:=[3,4] ▸ [3,4]

   Projektionen af a på b er: (a•b)·b·|b|^-2

   Man får: dotP(a,b)*1.*b/(norm(b))²) ▸ [−1.68,−2.24]

   Dvs. projektionen af a på b er (−1,68;−2,24)

Svar på opgave 9:

1. Man har først brug for at finde sidenlængden |AC|. Dette gøres ved hjælp af en cosinusrelation:

   solve(cos(89.°)=((58²+94²-ac²)/(2*58*94)),ac)|ac>0 ▸ ac=109.59

   Dernæst bruges en sinusrelation til at finde vinkel A:

   solve(sin(89.°)/109.59°=sin(a*1.°)/94°,a)|0<a<90 ▸ a=59.050

   Vinkel A er dermed lig med 59,05°

   Arealet af ΔABC er: 0,5·(højde)·(grundlinje) = 0,5·(58·sin(59,05°))·(109.59) = 2725,6

   Dvs. arealet af ΔABC er 2725,6

2. Man skal kende vinkel C. Den findes ved hjælp af reglen om, at summen af vinklerne i en trekant er 180°: ∠C = 180° - 89° - 59,05° = 31,95°. Desuden skal man bruge halvdelen af |BC|, som er 47. Dette er vist nedenfor:

   

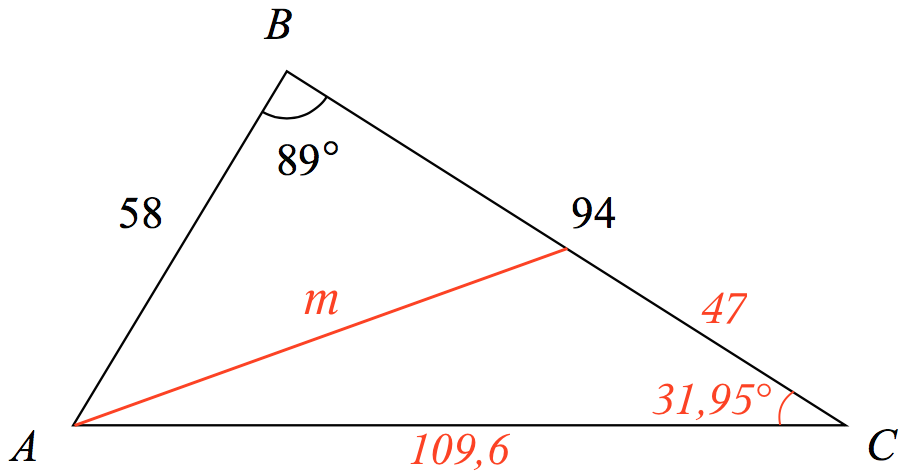
   Herefter bruger man en cosinusrelation til at finde medianen kaldet m:

   solve(cos(31.95°)=(109.59²+47²-m²)/(2*109.59*47),m)|m>0 ▸ m=74.014

   Dvs. længden af medianen fra hjørnet A til siden a er 74,01

Svar på opgave 10:

1. Tangenten til grafen for f i punktet P = (0,f(0)) kan skrives

   y = f '(0)·(x - 0) + f(0).

   Man opretter f i Ti-Nspire:

   f(x):=(x²+5*x+500)*exp(−x/100) ▸ Udført

   Man finder den afledede af f og kalder den fm:

   fm(x):=derivative(f(x),x) ▸ Udført

   Man bestemmer ligningen for tangenten gennem P:

   y=fm(0)*(x-0)+f(0) ▸ y=500

   Dvs. ligningen er y = 500

2. Man skal lave en fortegnsbestemmelse for f ':

   solve(fm(x)=0,x) ▸ x=0 or x=195 (find nulpunkter for f ')

   fm(−1.) ▸ −1.9797 (f ' er negativ og f dermed aftagende)

   fm(1.) ▸ 1.9207 (f ' er positiv og f dermed voksende)

   fm(200.) ▸ −1.3534 (f ' er negativ og f dermed aftagende)

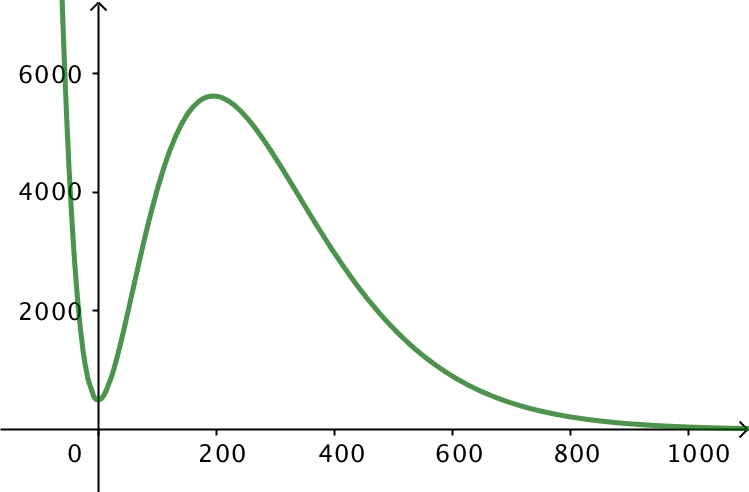
   Monotoniforhold: f er aftagende for x < 0, voksende for 0 < x < 195 og aftagende for x > 195

3. Nedenfor er grafen vist for x liggende mellem -100 og 1000:

   

Svar på opgave 11:

1. Man opretter c(x) i Ti-Nspire:

   c(x):=(12500*x-2500*x²)/(150+7.8^x)+90 ▸ Udført

   Man opretter dernæst c' og kalder den cm:

   cm(x):=derivative(c(x),x) ▸ Udført

   Man finder nulpunkter for c':

   solve(cm(x)=0,x) ▸ x=1.61955 or x=5.53479

   Man finder værdierne af c(x) i yderpunkterne for definitionsmængden og ved nulpunkterne af c' (størsteværdien er et af stederne):

   c(0) ▸ 90.

   c(7) ▸ 89.9801

   c(1.61955) ▸ 166.959 (største værdi)

   c(5.53479) ▸ 89.9147

   Det ses, at den største værdi af glukoseindholdet fås for x = 1,61955 og dermed er det tidspunkt, hvor glukoseindholdet i blodet er størst lig med 1,62 timer efter indtagelsen af måltidet.

2. Man løser ligningen c(x) = 130 mg/dl:

   solve(c(x)=130,x) ▸ x=0.550532 or x=2.66589

   Man undersøger monotoniforholdene mellem disse værdier, idet men ved, at c'(1,620) = 0:

   cm(1) ▸ 41.094 (c vokser mellem x = 0,5505 og x = 1,620)

   cm(2) ▸ −30.312 (c aftager mellem x = 1,620 og x = 2,666)

   Dette viser, at koncetrationen af glukose i blodet er større end 130 mg/dl fra t = 0,55 timer til t = 2,67 timer efter indtagelsen af et måltid.

   Længden af dette tidsrum er (2,666 - 0,5505) timer = 2,12 timer

Svar på opgave 12:

1. Man opretter f i Ti-Nspire:

   f(x):=x³-6*x²+32 ▸ Udført

   Man finder rumfanget ved hjælp af formlen for rumfanget af et legeme, der drejes om x-aksen:

   integral(π*(f(x))²,x,0.,4) ▸ 4779.53

   Dvs. rumfanget af omdrejningslegemet er 4779,5

2. Man integrerer f mellem x = 0 og x = 4:

   m=integral(f(x),x,0.,4) ▸ m=64. (arealet af M er 64)

   Man finder værdien af x for punktet, hvor f skærer y = 32:

   solve(f(x)=32,x) ▸ x=0 or x=6

   Man integrerer 32 - f(x) mellem x = 0 og x = 6:

   n=integral(32-f(x),x,0.,6) ▸ n=108. (arealet af N er 108)

   Dvs. forholdet mellem arealerne af M og N er 64/108 = 0,5926

Svar på opgave 13:

1. Nulhypotese: forkølelse er uafhængigt af kolde fødder

2. Man opretter et skema over observerede værdier som vist:

   

   Man opretter en 2×2 matrix med de observerede værdier i Ti-Nspire:

   obs:=[[13,77][5,85]] ▸ [[13,77][5,85]]

   Man laver en Chi-i-anden uafhængighedstest på matricen:

   χ²2way obs: stat.results ▸
   [["Titel","χ²-uafhængighedstest"]
   ["χ²",3.95062]
   ["PVal",0.046854]
   ["df",1.]
   ["ExpMatrix","[...]"]
   ["CompMatrix","[...]"]]

   Det ses at PVal = 0,047, som er mindre end 0,05 (5 %) og dermed forkastes nulhypotesen på et 5% signifikansniveau

Svar på opgave 14:

1. Man løser differentialligningen, hvor V(0) = 95 og D = 2800

   deSolve(v'=(1/7700)*(2800-40*v) and v(0)=95,t,v) ▸ v=25*exp(−2*t/385)+70

   Man opretter V(x) i Ti-Nspire:

   v(t):=25*exp(−2*t/385)+70 ▸ Udført

   Dvs. forskriften for V er 25·exp(−2·t/385) + 70

   Man finder V(45):

   v(45.) ▸ 89.7887

   Dvs. personens vægt 45 dage efter slankekurens start er 89,8 kg

2. Man skal finde en forskrift for V med startbetingelsen V(0) = 100:

   deSolve(v'=(1/7700)*(d-40*v) and v(0)=100,t,v) ▸ v=(100-d/40)*exp(−2*t/385)+d/40

   Man opretter den nye forskrift i Ti-Nspire og kalder den V1:

   v1(t):=(100-d/40)*exp(−2*t/385)+d/40 ▸ Udført

   Man skal finde de D, der giver vægten 100 kg - 5kg = 95 kg:

   solve(v1(90)=95.,d) ▸ d=3464.46

   Dvs. det daglige energiindtag skal være 3464,5 kcal.

Svar på opgave 15:

1. Man opretter punkterne A-C som stedvektorer i Ti-Nspire:

   a:=[0,3,3] ▸ [0,3,3]

   b:=[1,4,0] ▸ [1,4,0]

   c:=[6,0,3] ▸ [6,0,3]

   Man opretter vektorerne AB og AC:

   ab:=b-a ▸ [1,1,−3]

   ac:=c-a ▸ [6,−3,0]

   Man finder krydsproduktet af AB og AC:

   crossP(ab,ac) ▸ [−9,−18,−9]

   Dette krydsprodukt er en normalvektor til planen α. Man kalder normalvektoren til α for n og sætter den lig med 1/9 af AB×AC for at få pænere tal:

   n:=(1/9)*crossP(ab,ac) ▸ [−1,−2,−1]

   Man opretter punktet P med koordinaterne (x,y,z) som stedvektor:

   p:=[x,y,z] ▸ [x,y,z]

   Man opretter vektoren AP

   ap:=p-a ▸ [x,y-3,z-3]

   Hvis punktet P ligger i planen α, så skal der gælde, at skalarproduktet af AP og n er lig med 0. Dette sættes ind i Ti-Nspire:

   dotP(n,ap)=0 ▸ −x-2*y-z+9=0

   Dvs. ligningen for α er −x - 2·y - z + 9 = 0, der kan omskrives til x + 2·y + z = 9 som ønsket.

2. Retningsvektoren (r) for linjen l er (3k,1,k). Man opretter r i Ti-Nspire:

   r:=[3*k,1,k] ▸ [3*k,1,k]

   Denne vektor skal være vinkelret på planens normalvektor. Dvs. skalarproduktet af r og n skal være 0. Den fremkomne ligning løses med hensyn til k:

   solve(dotP(n,r)=0,k) ▸ k=−1/2

   Dvs. k skal være -1/2 for at linjen l ligger i planen α.