Kl. 9:00 - 10:00
Opgave 1
En parabel er bestemt ved ligningen:
y = 2x2 - 4x + 3
Bestem koordinatsættet til toppunktet.
Svar på opgave 1:
-
Parablens toppunkt kaldes (xT,yT). Der gælder, at (xT , yT) = (-b/(2·a) , c-b2/(4·a)).
Her er a = 2, b = -4 og c = 3.
Det giver : xT = -(-4)/(2·2) = 1 og yT = 3 - (-4)2/(4·2) = 1.
Dvs. koordinatsættet til toppunktet er (1,1)
Opgave 2
I et koordinatsystem er to vektorer givet ved
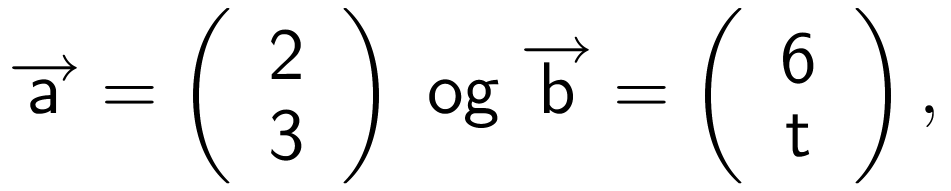
hvor t er et tal.
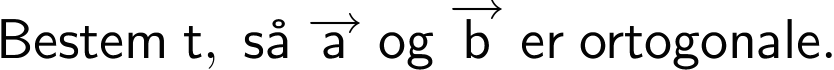
Svar på opgave 2:
-
Vektorerne a og b er ortogonale, når (og kun når) de er egentlige og a·b = 0
Man får: a·b = 0 ⇒ (2,3)·(6,t) = 0 ⇔ 2·6 + 3·t = 0 ⇔ 3t = -12 ⇔ t = -4.
Dvs. vektorerne a og b er ortogonale, når t = -4
Geogebra-løsning: Varier t for at se hvordan vinklen mellem vektorerne ændres. Vinklen måles her mod uret fra b til a. Bemærk at b ikke kan komme til at pege modsat den retning, som den har for t = -4, derfor er der ikke andre løsninger.
Se evt.geogebra.org, hvis der ikke kommer et billede frem.
Opgave 3
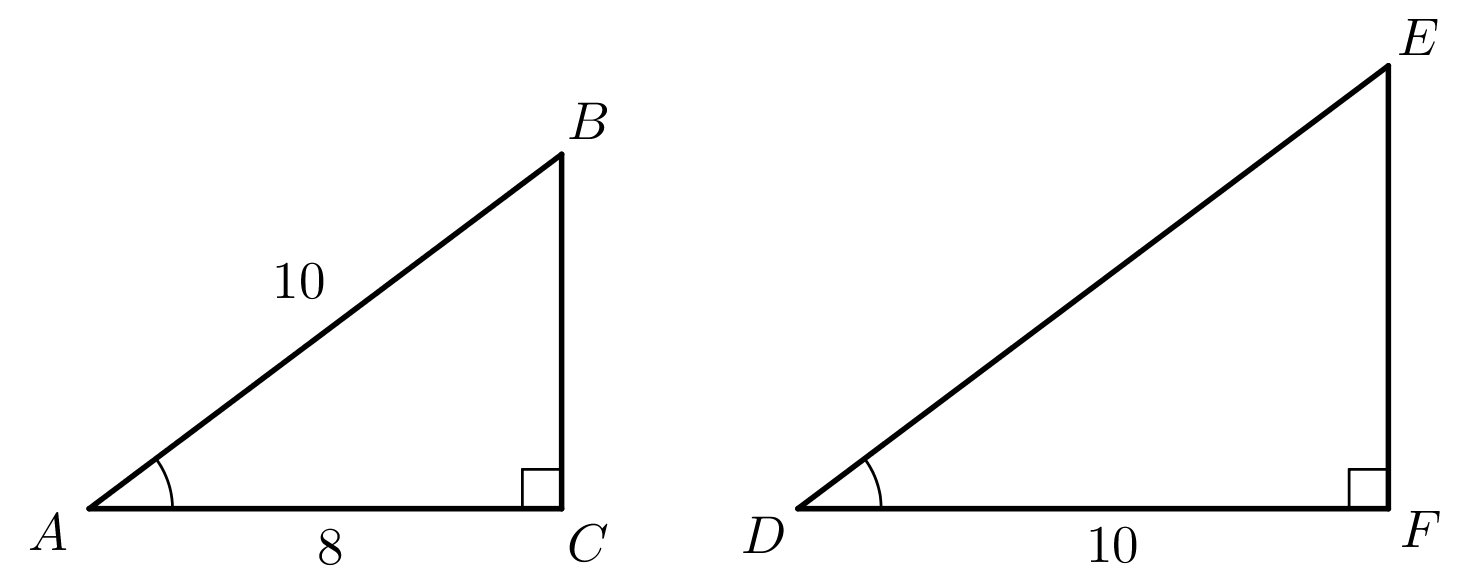
På figuren ses to ensvinklede trekanter ABC og DEF. Nogle af sidelængderne er angivet på figuren.
Bestem |EF|.
Svar på opgave 3:
-
Skaleringsfaktoren for trekant DEF i forhold til trekant ABC er |DF|/|AC| = 10/8 = 5/4. Dette giver følgende sammen med Pythagoras læresætning for den retvinklede trekant DEF:
|EF|2 + |DF|2 = |DE|2 ⇔
|EF|2 = |DE|2 - |DF|2⇒
|EF|2 = |DE|2 - 102 ⇒
|EF|2 = [(5/4)·|AB|]2 - 102⇒
|EF|2 = [(5/4)·10]2 - 102 ⇒
|EF|2 = 12,52 - 102 ⇒
|EF| = √[12,52 - 102] ⇒
|EF| = 7,50
Opgave 4
En funktion f er givet ved
f(x) = 3x2 + 4x
Bestem en forskrift for den stamfunktion til f, der går gennem punktet P(2,4).
Svar på opgave 4:
-
En vilkårlig stamfunktion til f(x) kaldes F(x).
F(x) = ∫ (3x2 + 4x) dx = x3 + 2x2 + k, hvor k er en reel konstant.
Der gælder, at F(2) = 4, dvs. 23 + 2·22 + k = 4 ⇒ k = -12.
Dvs. den stamfunktion til f, der går igenem P(2,4) er: F(x) = x3 + 2x - 12
Opgave 5
I et koordinatsystem i planen er en cirkel givet ved ligningen
x2 - 4x + y2 + 6y + 12 = 0
Bestem cirklens radius og koordinatsættet til dens centrum.
Svar på opgave 5:
-
Man skal omskrive cirklens ligning til formen: (x - a)2 + (y - b)2 = r2. Her er (a,b) koordinaterne til centrum og r lig med radius. Omskrivningen foretages ved at lave en kvadratkomplettering af venstresiden for x og y:
For led med x får man: x2 - 4x = x2 - 2·2x = x2 - 2·2x + 22 - 22 = (x - 2)2 - 4.
For led med y får man: y2 + 6y = y2 + 2·3·y = y2 + 2·3·y + 32 - 32 = (y + 3)2 - 9.
Man indsætter udtrykkene x2 - 4x = (x - 2)2 - 4 og y2 + 6y = (y + 3)2 - 9 i cirklens ligning:
x2 - 4x + y2 + 6y + 12 = 0 ⇒ (x - 2)2 - 4 + (y + 3)2 - 9 + 12 = 0 ⇔ (x - 2)2 + (y + 3)2 = 1 ⇔
(x - 2)2 + (y - (-3))2 = 12.
Dette giver: centrum = (2,-3) og radius = 1
Opgave 6
En funktion f er løsningen til differentialligningen
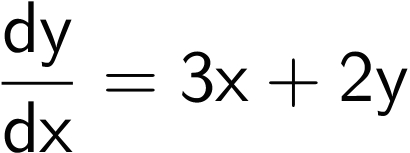
Det oplyses, at tangenten til grafen for f i punktet P(1,f(1)) har hældningen 9.
Bestem en ligning for tangenten til grafen for f i punktet P(1,f(1)).
Svar på opgave 6:
-
Ligningen for tangenten til f i punktet (1,f(1)) er
y = f´(1)·(x - 1) + f(1).
Man ved, at f´(1) = 9 fra oplysningen om grafens hældning og mangler derfor kun at finde f(1). Her benytter man, at når f er løsning til differentialligningen, så gælder: f´(x) = 3·x + 2·f(x) og dermed: f´(1) = 3·1 + 2·f(1) ⇔ f(1) = [f´(1) - 3]/2.
Dette indsættes i tangentens ligning: y = f´(1)·(x - 1) + [f´(1) - 3]/2 ⇒ y = 9·(x - 1) + [9 - 3]/2 ⇒ y = 9x - 6.
Dvs. tangentens ligning for f i punktet (1,f(1)) er y = 9x - 6
Kl. 10:00 - 14:00
Opgave 7
En biolog måler jævnligt koncentrationen af et bestemt pesticid i en forurenet sø. Resultaterne fremgår af nedenstående tabel.
| Tid efter første måling (døgn) | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 |
| Koncentration (ppm) | 278 | 206 | 138 | 110 | 81 | 58 | 49 | 32 |
I en model kan udviklingen i koncentrationen som funktion af tiden beskrives ved en funktion af typen
C(t) = b·at,
hvor C(t) betegner koncentrationen af pesticider i søen (målt i ppm) til tidspunktet t (målt i døgn efter første måling).
-
Benyt tabellens data til at bestemme konstanterne a og b.
-
Bestem hvor lang tid, der går efter første måling, før det er sundhedsmæssigt forsvarligt at bade i søen.
Det oplyses, at det er sundhedsmæssigt forsvarligt at bade i søen, når koncentrationen af pesticid er under 5 ppm.
Svar på opgave 7 i Ti-Nspire:
-
Man opretter lister med tider (t) og koncentrationer (C(t)):
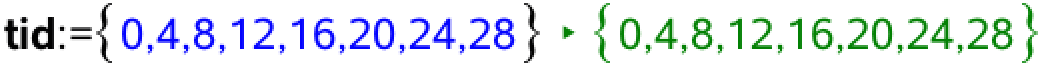

Man laver derpå en eksponentiel regression ved hjælp af kommandoen: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression... ▸ X-liste=tid, Y-liste=koncentration. Dette giver resulatet:

Dette viser at a = 0,9277 og b = 270,51
(Ti-Nspire bruger a og b modsat opgaven).
-
Ti-Nspire opretter automatisk funktionen f1(x), der kan bruges som C(t) (man må gerne bruge f1(t) i stedet for f1(x)). Man skal løse ligningen C(t) = 5 med hensyn til t:
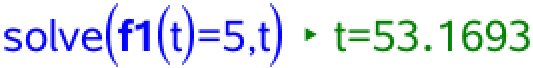
Dette viser, at det er sundhedsmæssigt forsvarligt at bade i søen efter 53,2 døgn
Svar på opgave 7 i Maple:
-
Med gympakken laver man en eksponentiel regression på tabellens to rækker, idet øverste række svarer til t og nederste række til C(t). Man får:
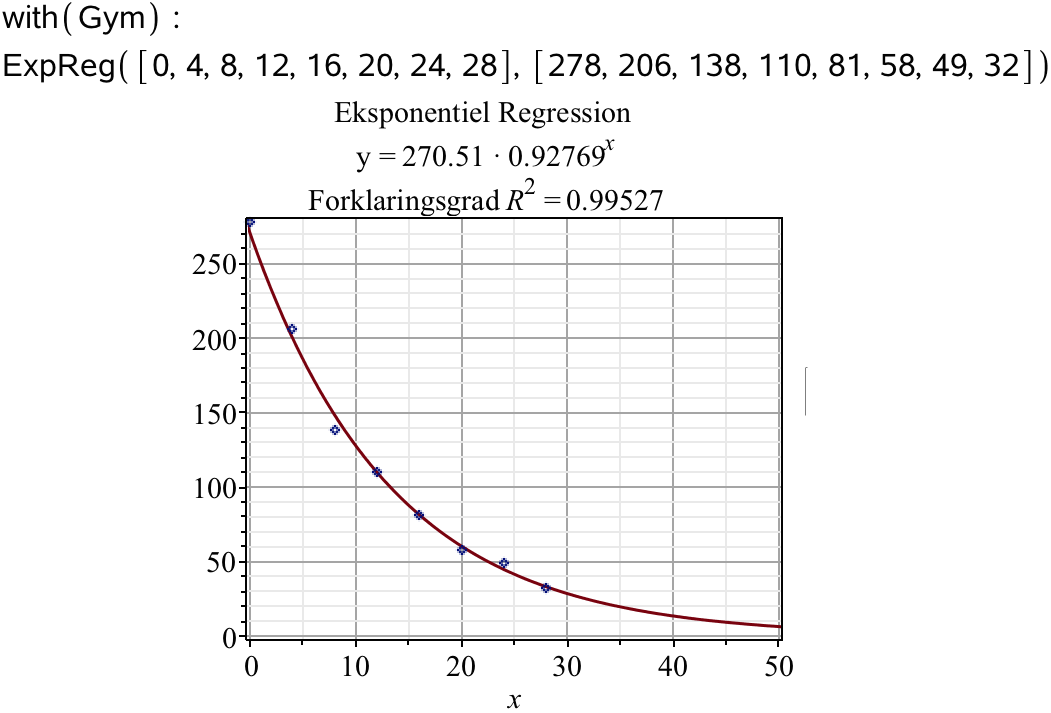
Dette viser (på fjerde linje i billedet), at a = 0,9277 og b = 270,51
-
Man opretter C(t) som funktion med de fundne værdier af a og b.

Dernæst løses ligningen C(t) = 5 med hensyn til t:
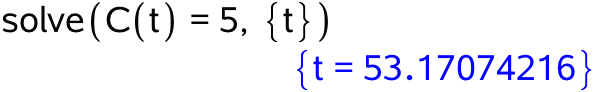
Dette viser, at det er sundhedsmæssigt forsvarligt at bade i søen efter 53,2 døgn
Opgave 8
f(x) = x3 - 3x2 - 9x + 11
-
Tegn grafen for f, og bestem koordinatsættet til hvert af grafens skæringspunkter med førsteaksen.
-
Bestem monotoniforholdene for f.
Svar på opgave 8 i Ti-Nspire:
-
Man opretter f(x) som funktion.
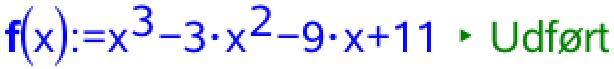
Grafen tegnes med nulpunkterne tilføjet:
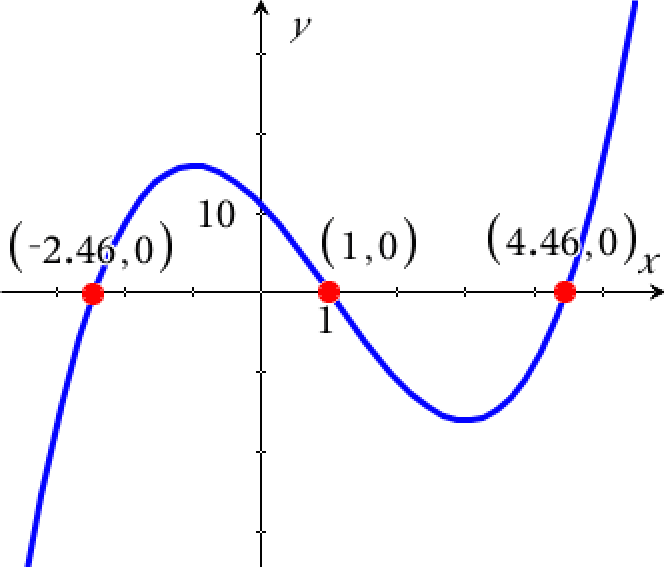
Nulpunkterne kan også findes som løsninger til ligningen f(x) = 0:
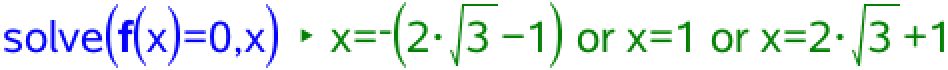
Dvs. koordinatsættene er (-2,464;0), (1,000;0) og (4,464;0)
(Man bestemmer selv om man vil bruge decimaltal eller hele tal med kvadratrødder.)
-
Man skal lave en fortegnsundersøgelse for f´(x). Først findes nulpunkter for f´(x):
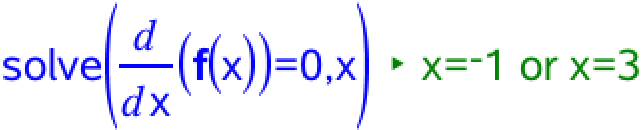
Dernæst undersøges fortegnet for f´(x) udenfor og mellem disse værdier (her for x = -2, x = 0 og x = 4):
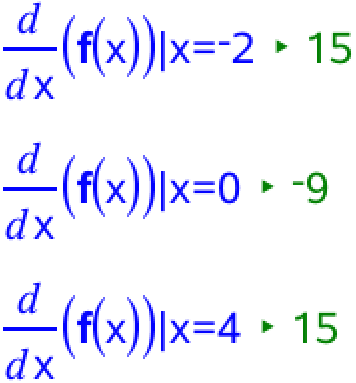
Dvs. f´(-2) > 0, f´(0) < 0 og f´(4) > 0. Dette viser, at f er voksende for x < -1, aftagende for -1 < x < 3 og voksende for x > 3
Svar på opgave 8 i Maple:
-
Man opretter f(x) som funktion.
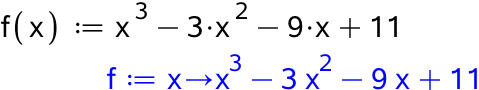
Dernæst laves et plot af f(x) for -6 ≤ x ≤ 8:
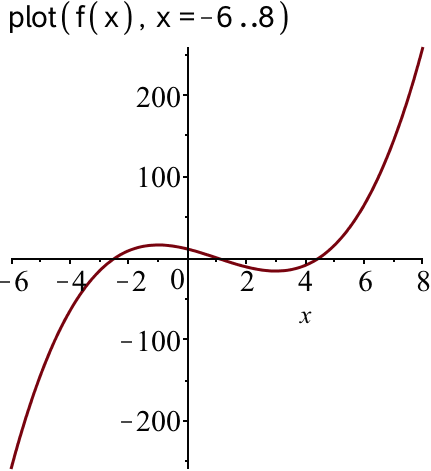
De x, hvor grafen for f skærer x-aksen, findes som løsninger til ligningen f(x) = 0:

Dvs. koordinatsættene er (-2,464;0), (1,000;0) og (4,464;0)
-
Man skal lave en fortegnsundersøgelse for f´(x). Først findes nulpunkter for f´(x):
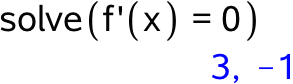
Dernæst undersøges fortegnet for f´(x), dels for en x-værdi mindre end -1, dels en mellem -1 og 3, dels en over x = 3:

Dvs. f´(-2) > 0, f´(0) < 0 og f´(4) > 0. Dette viser, at f er voksende for x < -1, aftagende for -1 < x < 3 og voksende for x > 3
Opgave 9
To funktioner f og g er givet ved
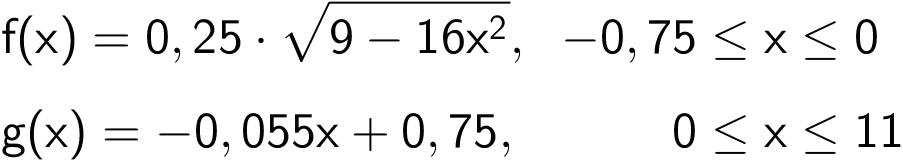
Graferne for f og g afgrænser sammen med koordinatsystemets førsteakse og linjen med ligningen x = 11 i første og anden kvadrant et område M, der har et areal.

-
Gør rede for, at f(0) = g(0), og bestem arealet af M.
-
Bestem skulpturens rumfang.
En skulptur har samme form som det omdrejningslegeme, der fremkommer, når M drejes 360° om førsteaksen. Enheden på koordinatsystemets akser er meter.
Svar på opgave 9 i Ti-Nspire:
-
Man opretter f og g som funktioner
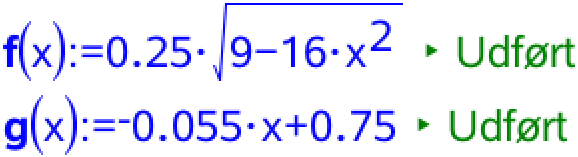
Man bestemmer f(0) og g(0), der ses at være ens, som man skulle vise:
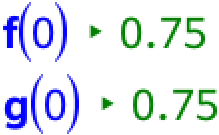
Arealet af M bestemmes som integralet af f i dennes definitionsinterval plus integralet af g i dennes definitionsinterval:
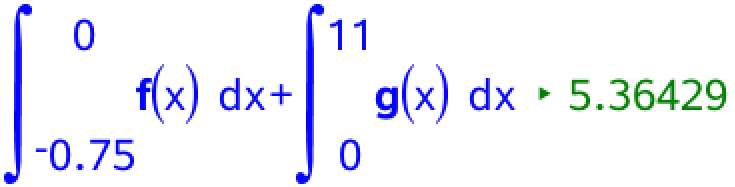
Dvs. arealet af M er 5,36 m2
-
Rumfanget findes ved hjælp af formlen for rumfanget af et omdrejningslegeme ved rotation om x-aksen:
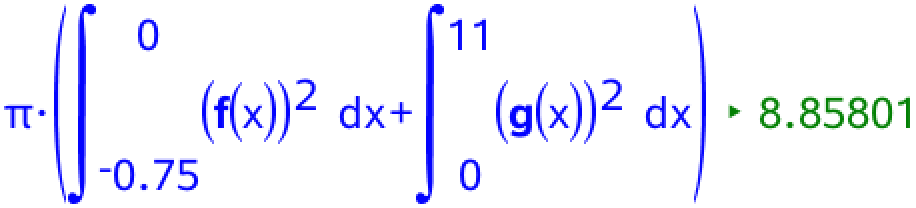
Dvs. rumfanget af skulpturen er 8,86 m3
Svar på opgave 9 i Maple:
-
Man opretter f og g som funktioner
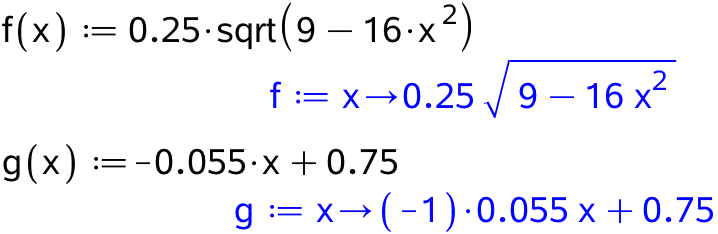
Man bestemmer f(0) og g(0), der ses at være ens, som man skulle vise:

Arealet af M bestemmes som integralet af f i dennes definitionsinterval plus integralet af g i dennes definitionsinteval:
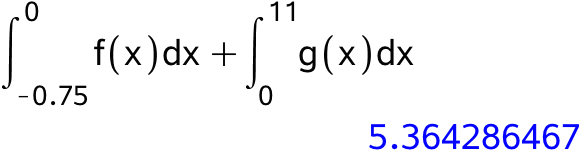
Dvs. arealet af M er 5,36 m2
-
Rumfanget findes ved hjælp af formlen for rumfanget af et omdrejningslegeme ved rotation om x-aksen:
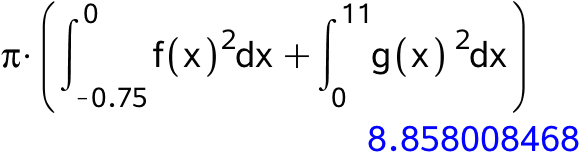
Dvs. rumfanget af skulpturen er 8,86 m3
Opgave 10
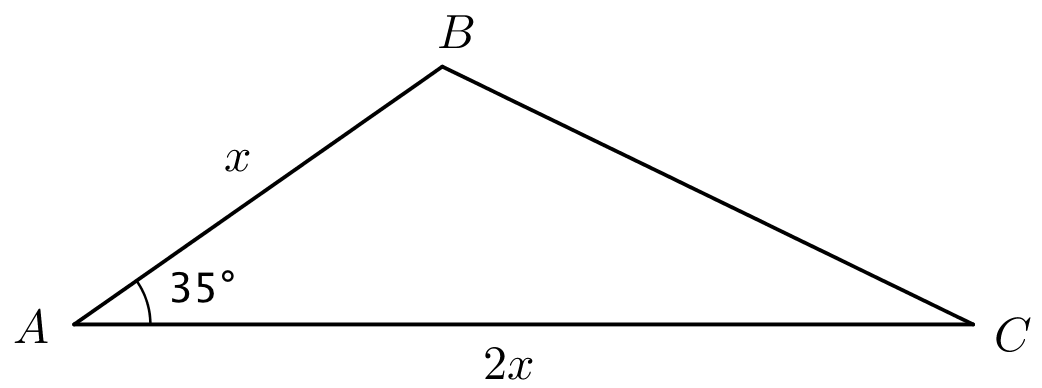
I trekant ABC er |AB| = x, |AC| = 2x og ∠A = 35°.
-
Bestem x, når |BC| = 5.
-
Bestem x, når arealet af ABC er 20.
Svar på opgave 10 i Ti-Nspire:
-
Man kender en vinkel og dens modstående side. Desuden kender man en sammenhæng mellem de hosliggende sider.
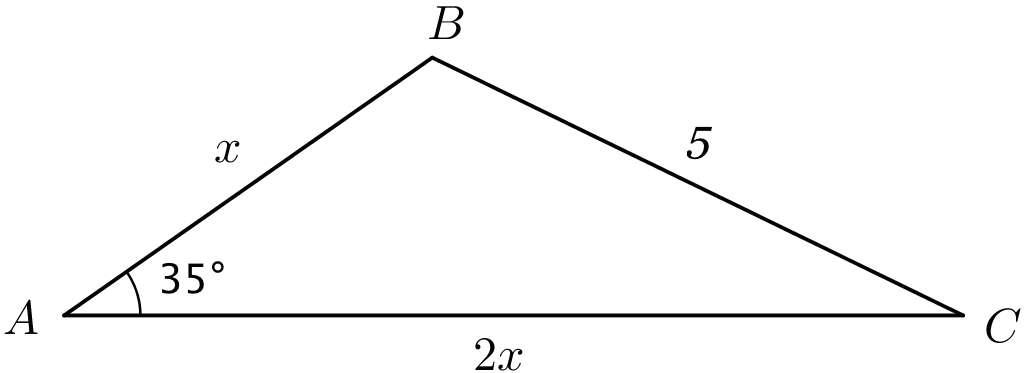
Man sætter oplysningerne ind i cosinusrelationen og løser den ligning, som man får, med hensyn til x, idet man kun ser på positive løsninger:
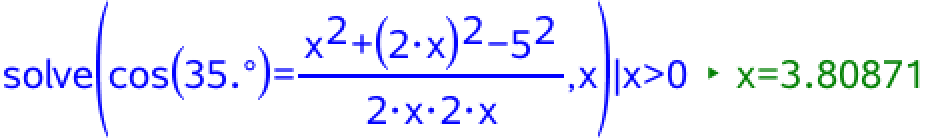
Dvs. x = 3,81
-
Arealet af trekant ABC er 0,5·grundlinje·højde. Grundlinje = 2x og højde = x·sin(35°). Dvs. man skal løse ligningen: 0,5·2x·x·sin(35°) = 20 med hensyn til x. Dette giver:
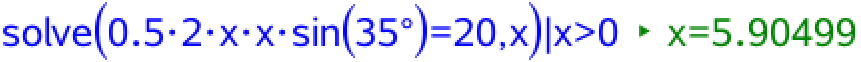
Dvs. x = 5,90
Svar på opgave 10 i Maple:
-
Man kender en vinkel og dens modstående side. Desuden kender man en sammenhæng mellem de hosliggende sider.
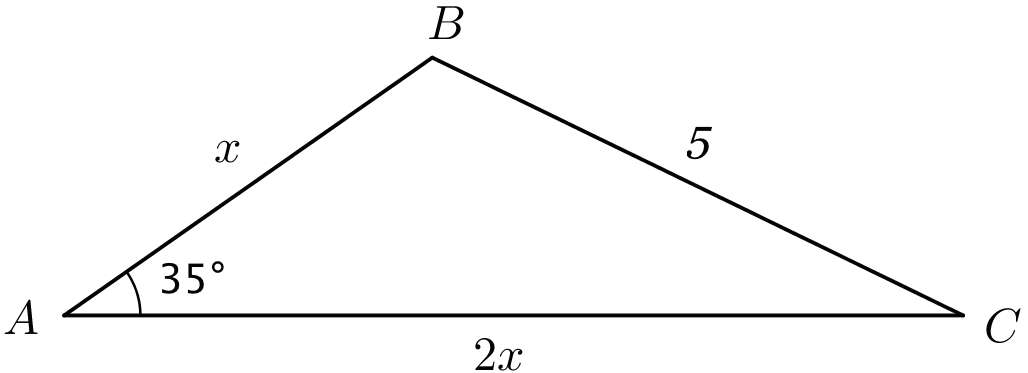
Man sætter oplysningerne ind i cosinusrelationen og løser den ligning, som man får, med hensyn til x, idet man kun ser på positive løsninger:
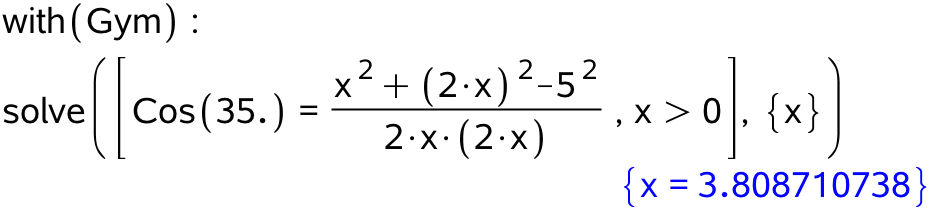
Dvs. x = 3,81
(Man bruger gympakken for at få adgang til Cos(v), der opfatter v som målt i grader. Funktionen cos(v) opfatter v som målt i radianer.)
-
Arealet af trekant ABC er 0,5·grundlinje·højde. Grundlinje = 2x og højde = x·sin(35°). Dvs. man skal løse ligningen: 0,5·2x·x·sin(35°) = 20. Dette giver (stadig med brug af gympakken):
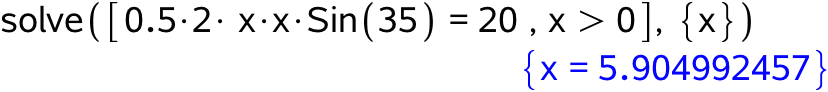
Dvs. x = 5,90
Opgave 11
I en bestemt kommune ønsker man at undersøge, om antallet af hjemmeboende børn i en husstand afhænger af, om der er kæledyr i familien. Resultatet fremgår af tabellen.
| Et eller flere kæledyr | Ingen kæledyr | |
| Ingen hjemmeboende børn | 133 | 202 |
| Et hjemmeboende barn | 24 | 28 |
| To eller flere hjemmeboende børn | 46 | 37 |
-
Opstil en nulhypotese, der kan anvendes til at teste, om der er sammenhæng mellem kæledyr i husstanden og antallet af hjemmeboende børn i husstanden, og opstil på grundlag heraf en tabel over de forventede værdier.
-
Bestem χ2-teststørrelsen, og undersøg, om nulhypotetsen kan forkastes på et 5 % signifikansniveau.
Svar på opgave 11 i Ti-Nspire:
-
Man skal lave en Chi-i-anden uafhængighedstest. Nulhypotesen er, at det som står i overskrifterne vandret er uafhængigt af det, som står i overskrifterne lodret, dvs.:
antallet af kæledyr er uafhængigt af antallet af hjemmeboende børn
Man opretter en matrix kaldet "obs" til de observerede værdier (matricens navn er underordnet). Man vælger menuerne: Beregninger ▸ Matricer og vektorer ▸ Opret ▸ Matrix...(3 rækker og 2 kolonner) og får:
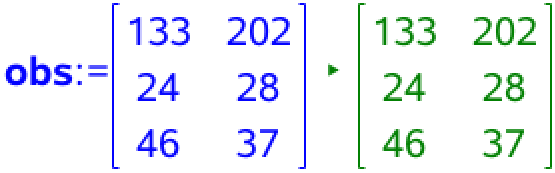
Man laver en Chi-i-anden uafhængighedstest på tabellens tal ved hjælp af kommendoerne: Beregninger ▸ Statistik ▸ Statistiske tests ▸ Χ2-Uafhængighedstest ▸ Observeret Matrix (vælg "obs"). Man får resultatet:

Når dette er gjort, finder man de forventede værdier ved hjælp af følgende kommando:

Dette kan evt. indsættes i tabellen:
Et eller flere kæledyr Ingen kæledyr Ingen hjemmeboende børn 144,69 190,31 Et hjemmeboende barn 22,460 29,540 To eller flere hjemmeboende børn 35,849 47,151 -
Det ses af resultat-skemaet fra opgave a), at p-værdien er 0,03 eller 3 %.

Da p-værdien er mindre end 5 % forkastes nulhypotesen
Svar på opgave 11 i Maple:
-
Man skal lave en Chi-i-anden uafhængighedstest. Nulhypotesen er, at det som står i overskrifterne vandret er uafhængigt af det, som står i overskrifterne lodret, dvs.:
antallet af kæledyr er uafhængigt af antallet af hjemmeboende børn.
Man bruger gympakken og opretter en matrix med tabellens tal:
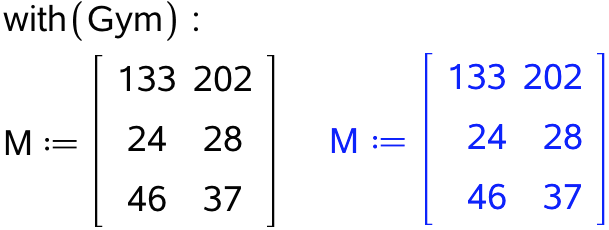
De forventede værdier findes med gympakkens kommando forventet():

Disse værdier indsættes i tabellen:
Et eller flere kæledyr Ingen kæledyr Ingen hjemmeboende børn 144,69 190,31 Et hjemmeboende barn 22,460 29,540 To eller flere hjemmeboende børn 35,849 47,151 -
Stadig med gympakken laver man en Chi-i-anden uafhængighedstest på de oprindelige data ved hjælp af ChiKvadratUtest() kommandoen:
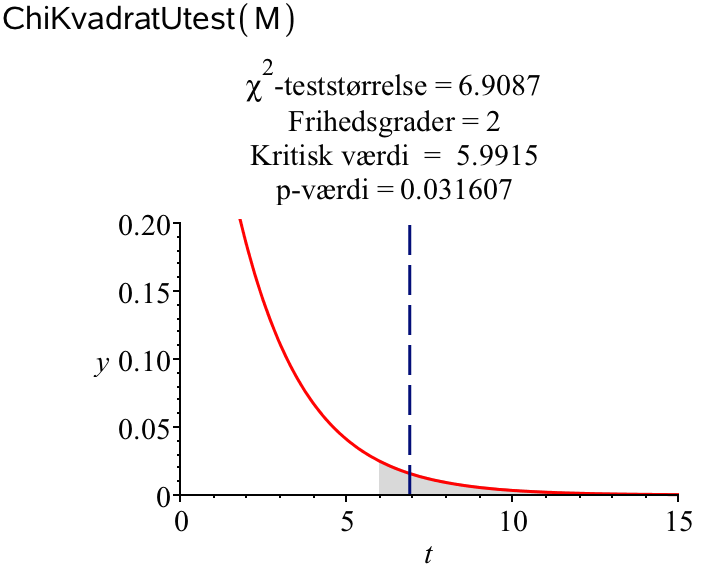
Det ses, at p-værdien er 0,03 eller 3 %. Da p-værdien er mindre end 5 % forkastes nulhypotesen
(Man kan også sige, at teststørrelsen (vist ved den stiplede linje) er større end den kritiske værdi eller ligger i det kritiske område (her vist med grå farve)).
Opgave 12
En persons alkoholpromille afhænger af flere faktorer, bl.a. mængden af indtaget alkohol, tiden efter indtaget, personens køn og personens vægt.
I en model er alkoholpromillen P(x) for kvinder til tidspunktet x (målt i timer efter indtagelse af alkohol) givet ved
P(x) = -0,15x + 20·(a/M),
hvor M er kvindens vægt i kg., og a er antallet af genstande, som indtages til tiden x = 0.
Anne vejer 70 kg, og Bente vejer 50 kg. De to kvinder indtager samtidig hver 4 genstande.
-
Benyt modellen til at bestemme, hvor meget længere det varer for Bente end for Anne at få en alkoholpromille på under 0,5.
-
Benyt modellen til at bestemme, hvor mange genstande Anne højst kan indtage, hvis hun ønsker en alkoholpromille på 0 efter 3 timer.
Svar på opgave 12 i Ti-Nspire:
-
Modellen viser, at der er en lineær sammenhæng mellem tid og alkohol promille. Promillen er størst lige efter indtagelse af alkohol og aftager derefter.
Man skal løse ligningen P(x) = 0,5 med hensyn til x for både Bente og Anne. Man opretter først P(x) som funktion:
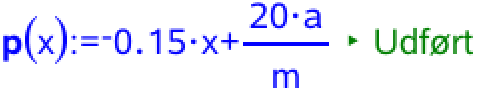
Derefter bruges solve-kommandoen for først Anne og så Bente med antal genstande og deres vægt indsat:
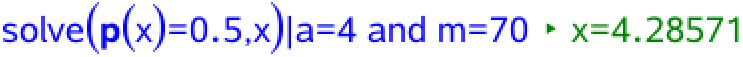
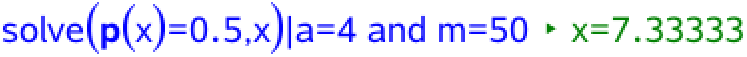
Dette viser, at det tager 4,29 timer for Anne at nå ned på en promille af 0,5, og at det tager 7,33 timer for Bente. Det tager dermed 7,33 - 4,29 timer = 3,05 timer længere for Bente end for Anne at nå ned på en promille på 0,5.
-
Her skal man løse ligningen P(3) = 0 med hensyn til a for M = 70. Dernæst skal man finde den heltallige værdi af a, der giver en promille på 0 eller derunder efter 3 timer. Man får:

Dermed er antallet af genstande, som Anne maksimalt kan indtage, 1,6
(Hvis der ønskes et helt antal genstande, så er facit 1.)
Svar på opgave 12 i Maple:
-
Modellen viser, at der er en lineær sammenhæng mellem tid og alkohol promille. Promillen er størst lige efter indtagelse af alkohol og aftager derefter.
Man skal løse ligningen P(x) = 0,5 med hensyn til x for både Bente og Anne. Man opretter først P(x) som funktion:
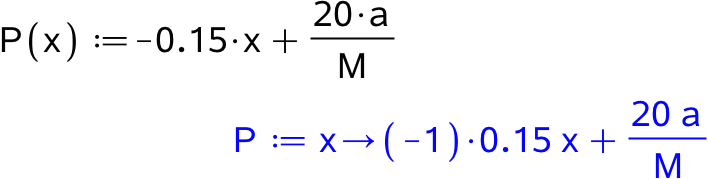
Derefter bruges solve-kommandoen for begge kvinder med deres tal indsat:
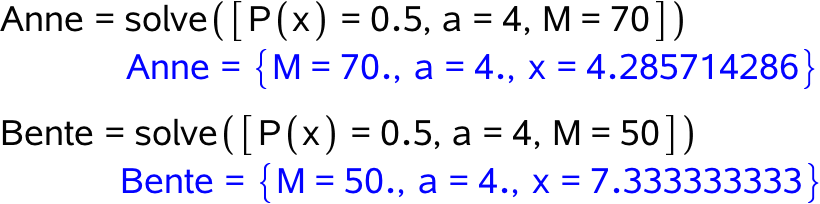
Dette viser, at det tager 4,29 timer for Anne at nå ned på en promille af 0,5, og at det tager 7,33 timer for Bente.
Det tager dermed 7,33 - 4,29 timer = 3,05 timer længere for Bente end for Anne at nå ned på en promille på 0,5.
-
Her skal man løse ligningen P(3) = 0 med hensyn til a for M = 70. Dernæst skal man finde den heltallige værdi af a, der giver en promille på 0 eller derunder efter 3 timer. Man får:
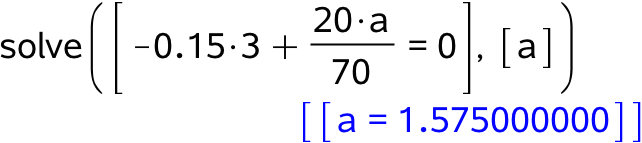
Dermed er antallet af genstande, som Anne maksimalt kan indtage, 1,6
(Det er usikkert, om der ønskes et helt antal genstande. I givet fald er facit 1.)
Opgave 13
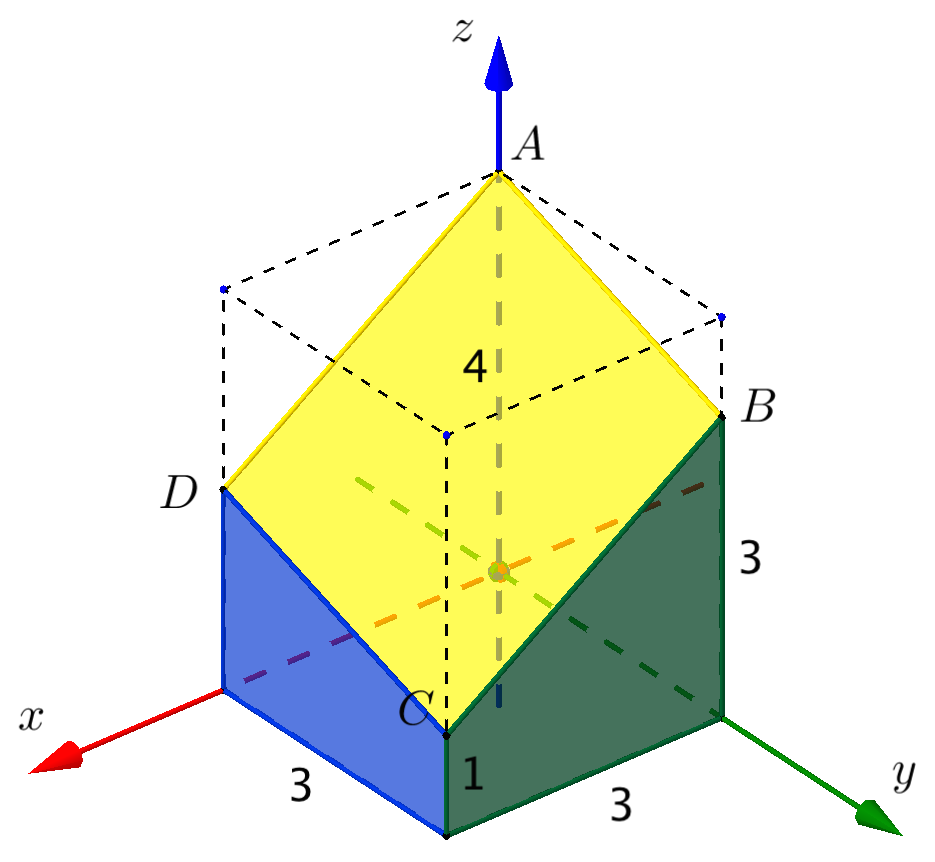
På figuren ses en model af en klods, der har kvadratisk bund med sidelængden 3, indtegnet i et koordinatsystem. Klodsen er placeret således, at bunden ligger i xy-planen, en side ligger i xz-planen og en anden side ligger i yz-planen.
Planen α gennemskærer klodsens kanter i punkterne A, B, C og D.
Det oplyses, at punkterne A, B og C ligger henholdsvis 4, 3 og 1 enheder over xy-planen (se figuren).
-
Gør rede for, at planen α er bestemt ved ligningen 2x + y + 3z = 12, og bestem koordinatsættet til D.
-
Bestem den stumpe vinkel mellem α og xz-planen.
Svar på opgave 13 i Ti-Nspire:
-
Man finder koordinaterne til A, B og C ved først at gå parallelt med først z-aksen, derefter y-aksen og til sidst x-aksen mod origo. Undervejs måler man, hvor langt man bevæger sig, og om man er på den positive eller negative del af den akse, som man bevæger sig på.
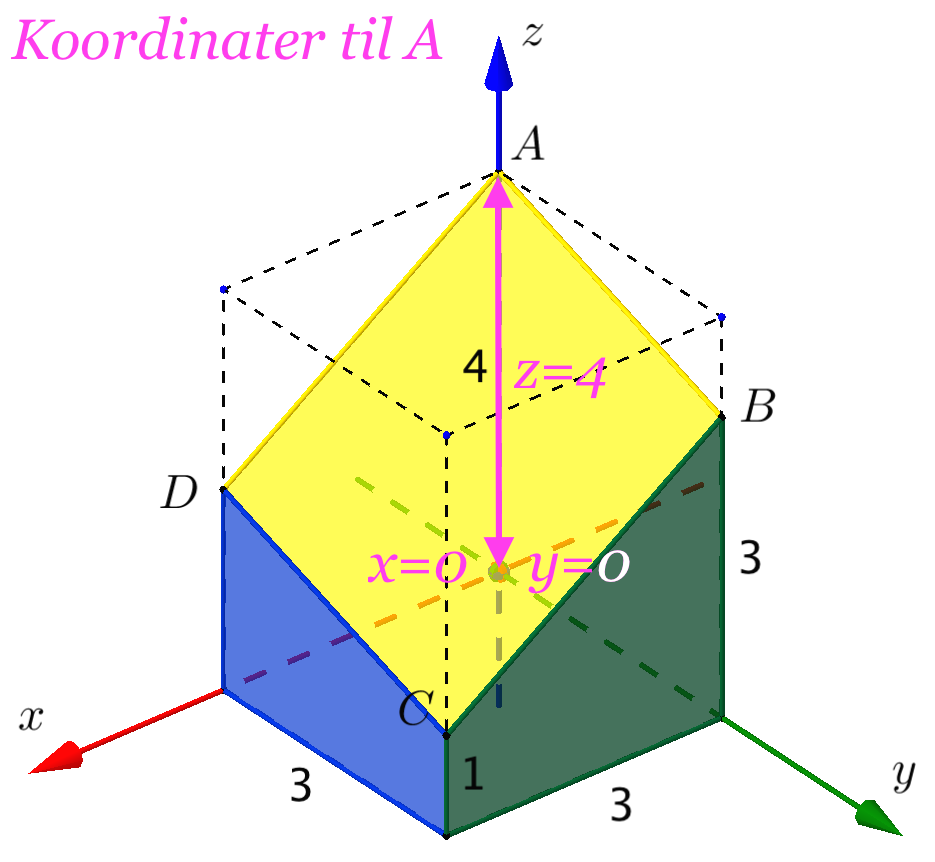
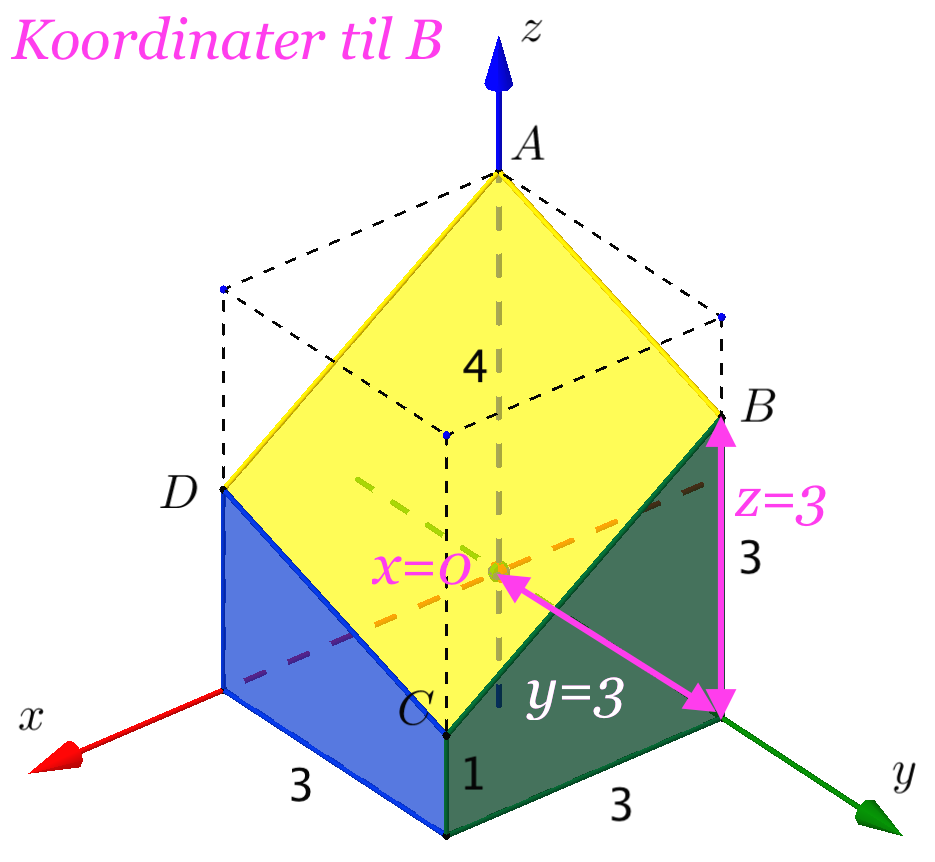
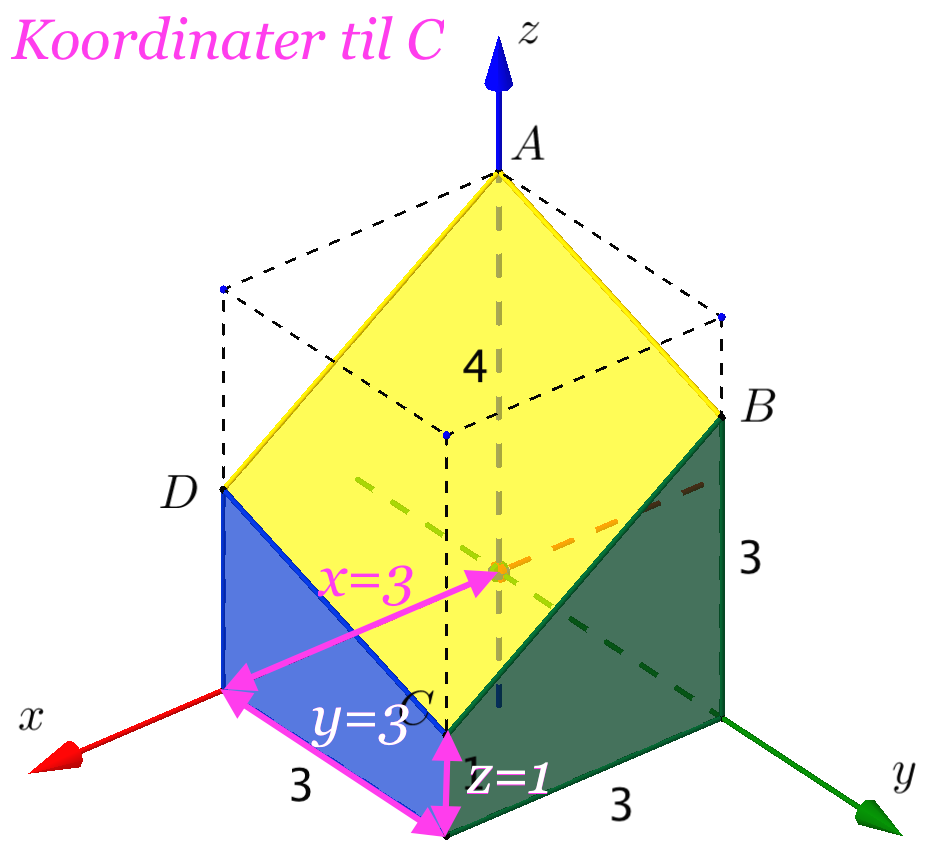
Man opretter de tre punkter som stedvektorer i Ti-Nspire:

Man opretter de to vektorer AB og AC, der ikke er parallelle og begge ligger i α:

Man tager krydsproduktet af AB og AC, der gemmes som normalvektoren n til α:
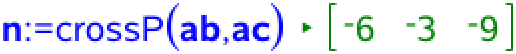
For en punkt P = (x,y,z) i α gælder, at skalarproduktet af vektoren AP (der ligger i α) og α's normalvektor n giver 0. Man tager derfor skalar- eller prikproduktet af de to vektorer ved hjælp af dotP() kommandoen:
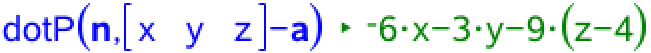
Dette skalarprodukt kan omskrives til -6x - 3y - 9z + 36, som sat lig med 0 giver: -6x - 3y - 9z + 36 = 0. Dette kan igen omskrives til følgende ligning for planen α: 2x + y + 3z = 12, som er det man skulle vise.
Man kender D's x- og y-koordinater, som er x = 3 og y = 0. Dette er fundet som vist nedenunder.
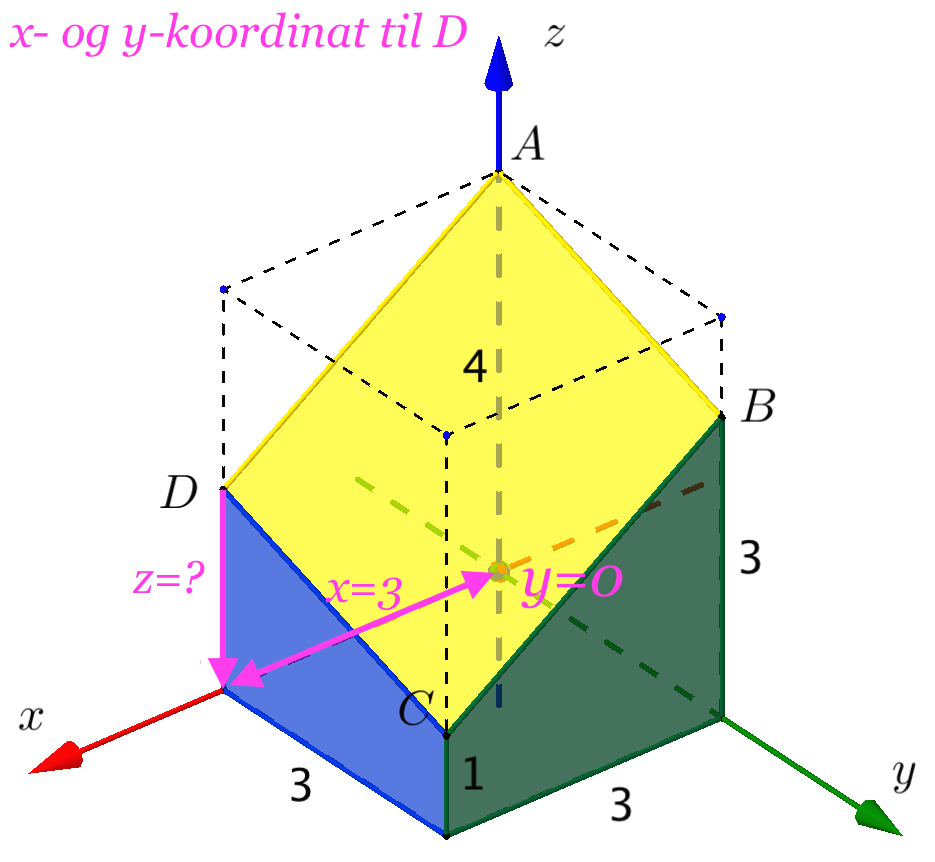
z-koordinaten for D er ukendt, men findes ved at indsætte x = 3 og y = 0 i α's ligning:
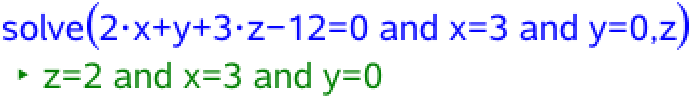
Dette giver z = 2 og dermed at D = (3,0,2)
-
xz-planen har normalvektoren m = (0,1,0). Denne vektor oprettes:
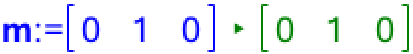
Ved hjælp af solve()-kommandoen finder man den stumpe vinkel mellem α og xz-planen som den stumpe vinkel mellem planernes normalvektorer. Hertil bruger man formlen for vinklen mellem to vektorer hvori indgår kommandoerne dotP()- (skalarproduktet) og norm() (længden af en vektor):
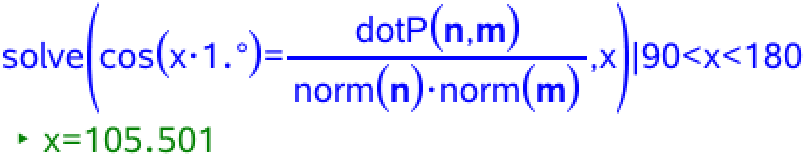
Dvs. den stumpe vinkel mellem α og xz-planen er 105,5°
Svar på opgave 13 i Maple:
-
Man finder koordinaterne til A, B og C ved først at gå parallelt med først z-aksen, derefter y-aksen og til sidst x-aksen mod origo. Undervejs måler man, hvor langt man bevæger sig, og om man er på den positive eller negative del af den akse, som man bevæger sig på.
Dette er vist på de tre tegninger nedenunder:
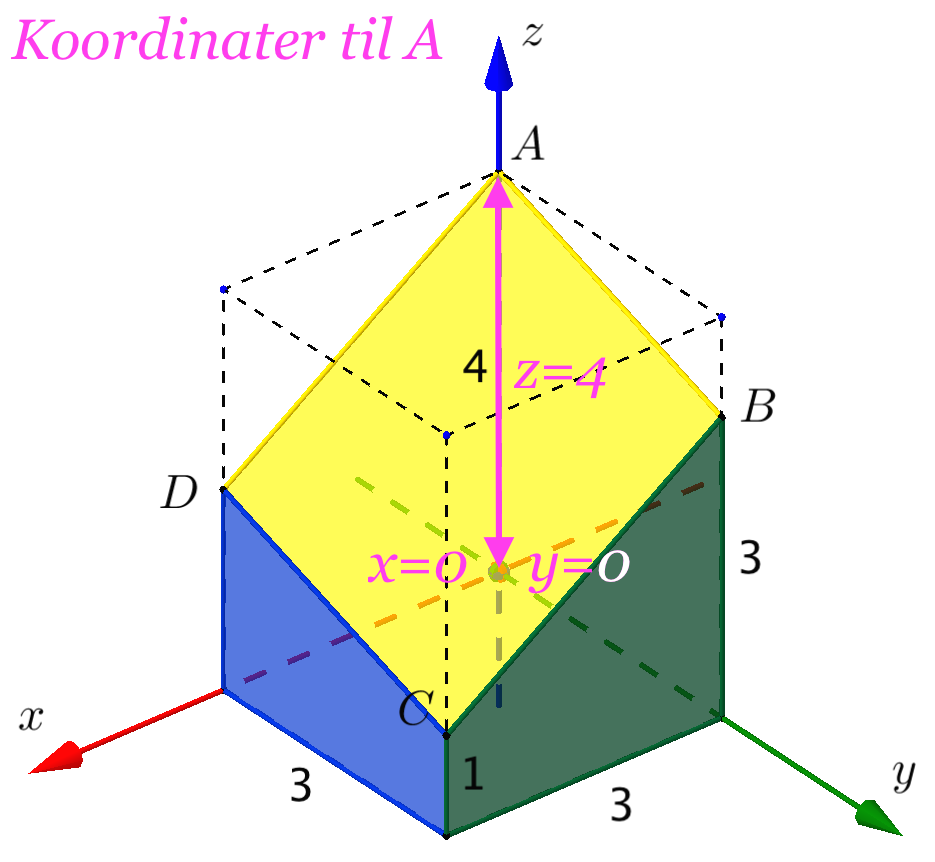
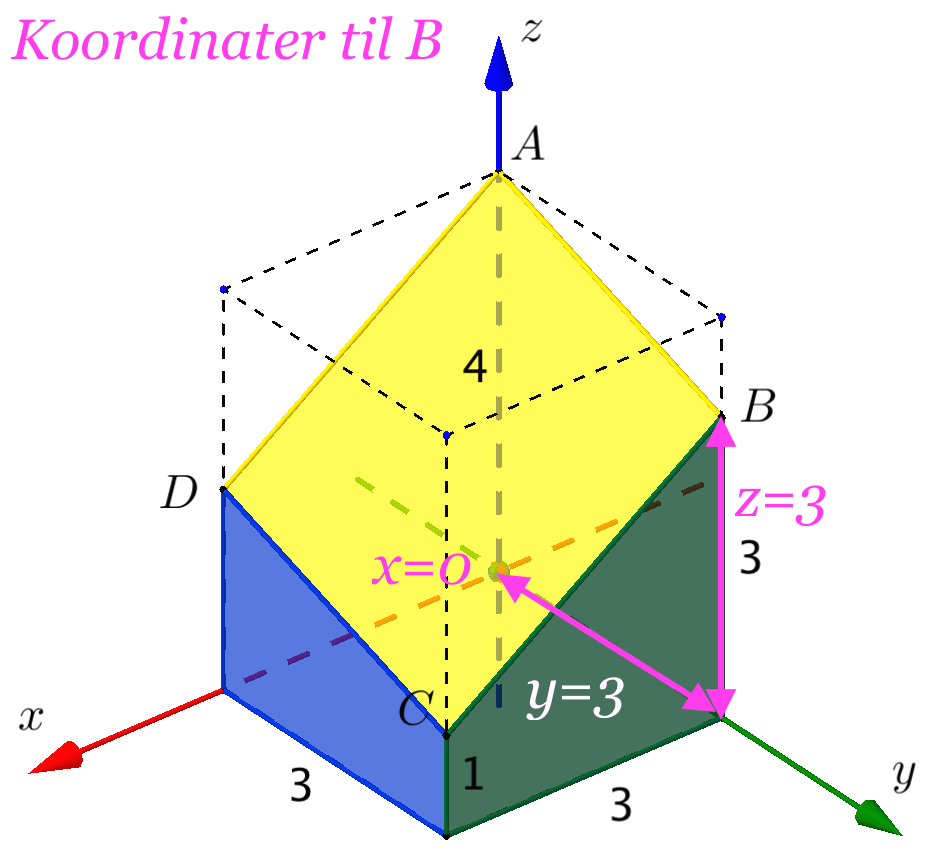
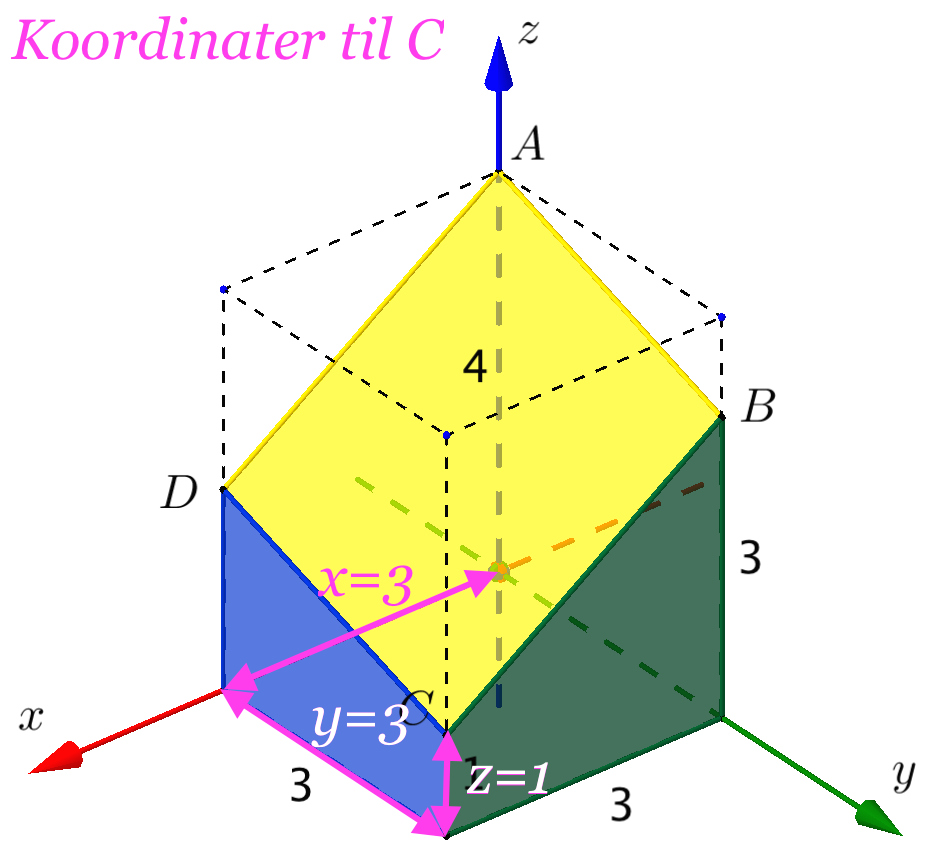
Man skal bruge pakken geom3d. Man opretter derefter punkterne A, B og C som vist:

Ved hjælp af punkterne A, B og C opretter man planen α:
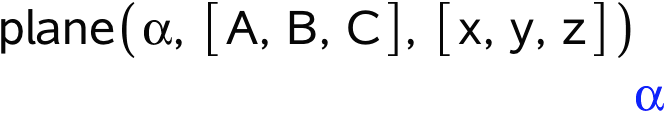
Til sidst får man Maple til at skrive planens ligning:
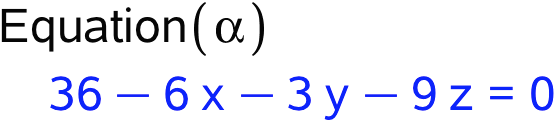
Dette kan ved at dividere igennem med -3 og flytte det konstante led over på højresiden omskrives til følgende ligning for α: 2x + y + 3z = 12, hvilket skulle vises.
Man ved at punktet D ligger i planen α, da α indeholder den gule firkant. Af nedenstående tegning fremgår det, at x-koordinaten til D er 3, og at y-koordinaten er 0.
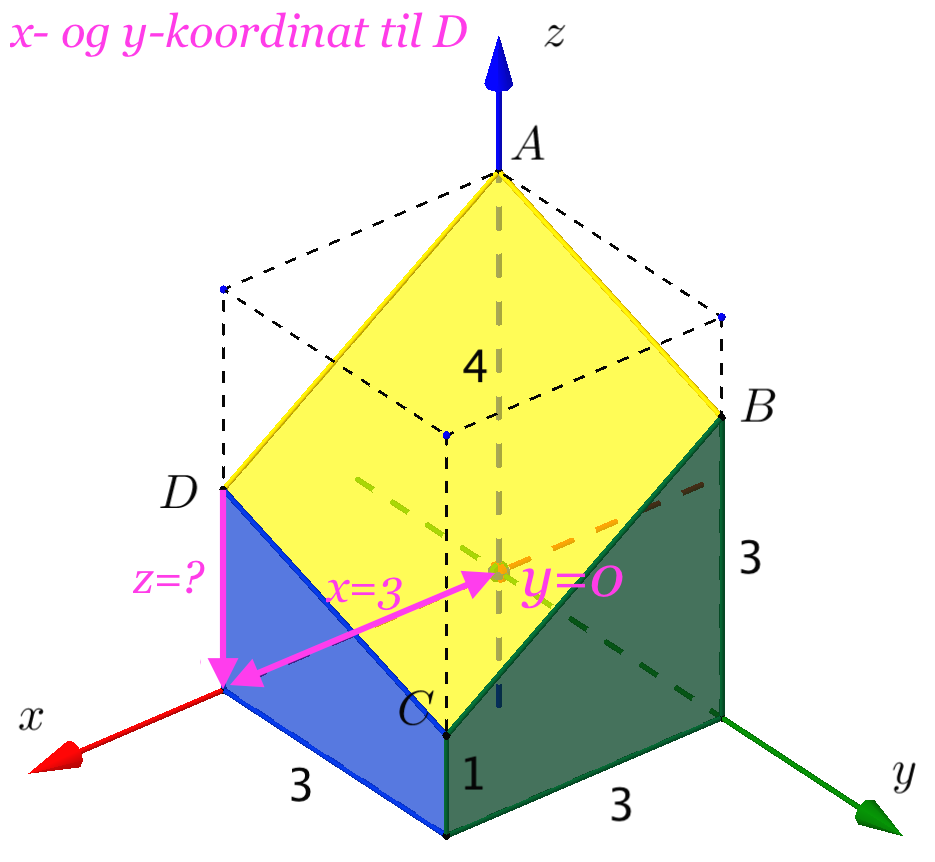
Man mangler derfor kun at finde z-koordinaten, som findes af ligningen for α ved at indsætte x = 3 og y = 0 og derpå løse ligningen med hensyn til z:
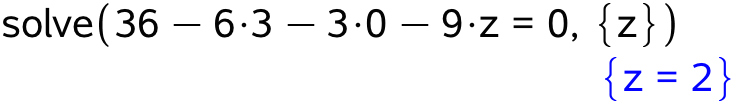
Dermed er D = (3,0,2).
-
xz-planen har ligningen y = 0 (y-aksen er den af akserne, der ikke indgår i planens navn). Denne ligning bruges til at oprette planen i Maple (planen kaldes xz som vist):
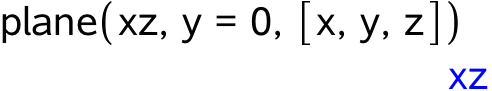
Dernæst bruges geom3d-kommandoen FindAngle() til at finde vinklen mellem α og xz-planen:
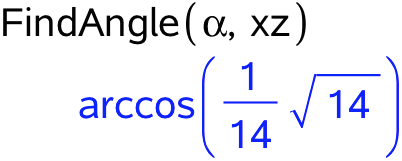
Man bruger dernæst evalf() kommandoen for at få resultatet som decimaltal:
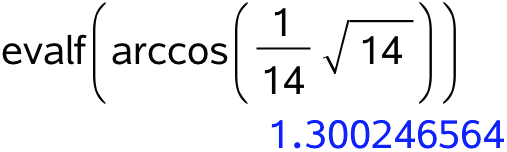
Dette omskrives fra radianer til grader:

Dette er den spidse vinkel mellem α og xz-planen. Dvs. den stumpe vinkel er 180° - 74,5° = 105,5°
Opgave 14
En nyåbnet butik i en lufthavn sælger kaffe til de rejsende. Butikkens ejere forventer, at væksthastigheden for det daglige salg af kaffe er proportional med det daglige salg af kaffe.
Tiden t måles i antal døgn efter åbningen af butikken, og det daglige salg af kaffe, f(t), måles i antal kopper. Proportionalitetskonstanten forventes at være 0,025.
-
Opstil en differentialligning, der beskriver udviklingen i det daglige salg af kaffe.
-
Bestem en forskrift for N(t), og benyt modellen til at bestemme det daglige salg af kaffe 30 døgn efter åbningen af butikken.
-
Tegn grafen for N i et passende interval, og benyt modellen til at bestemme den øvre grænse for det daglige salg af kaffe.
Efter nogen tid viser det sig, at følgende differentialligning er en bedre model for det daglige salg af kaffe:
dN/dt = 0,00017·N·(200 - N),
hvor N(t) angiver det daglige salg af kaffe (målt i antal kopper), og t angiver tiden (målt i antal døgn efter åbningen af butikken).
Det oplyses, at butikken sælger 50 kopper kaffe den første dag efter åbningen af butikken.
Svar på opgave 14 i Ti-Nspire:
-
Differentialligningen er
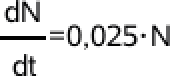
-
Man anvender begyndelsesbetingelsen N(0) = 50 og løser ligningen:
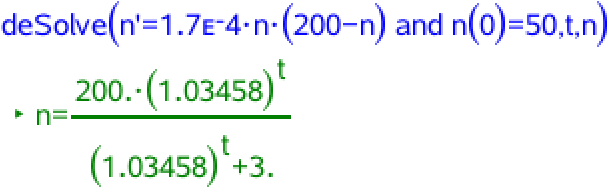
Dvs. løsningen er:
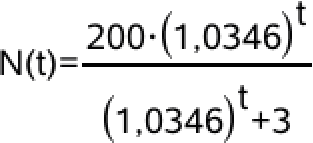
(Den første dag opfattes her som t = 0, da det er den laveste værdi for t.)
-
Man opretter N(t) som funktion:
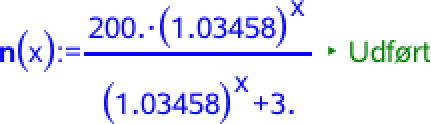
Man afbilder grafen af N(t) for t (her erstattet af x) mellem 0 og 200:
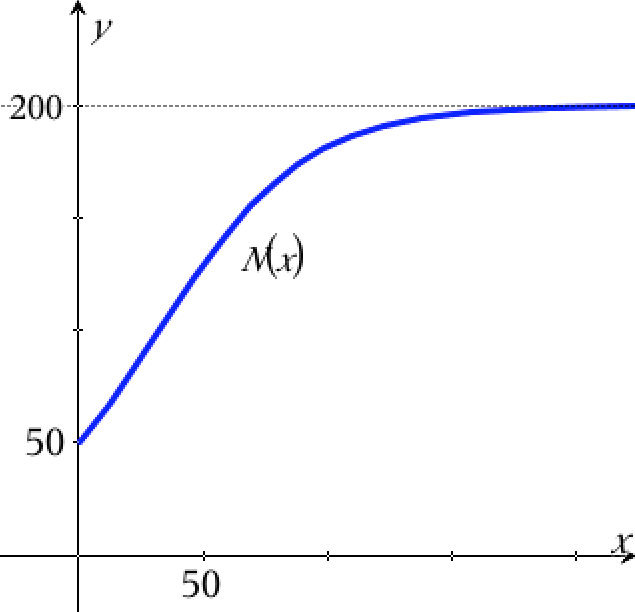
Ud fra grafen bedømmer man grænseværdien (toppen af figuren) til 200 kopper om dagen.
Svar på opgave 14 i Maple:
-
Differentialligningen er dN(t)/dt = 0,025·N(t) (eller kortere: dN/dt = 0,025·N)
-
Man anvender begyndelsesbetingelsen N(0) = 50 og løser ligningen i Maple:

Dvs. løsningen er:
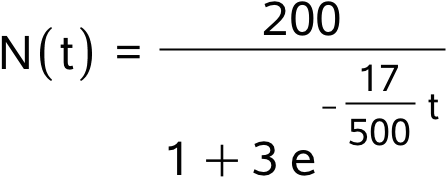
(Bemærk at begyndelsesbetingelsen både kan forstås som om t = 0 og t = 1. Her vælges t = 0, da det er den laveste værdi, som dermed står for den første dag.)
-
Man opretter N(t) som funktion i Maple:
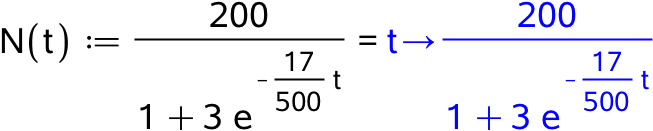
Man afbilder grafen af N(t) for t mellem 0 og 250 samt for N(t) mellem 0 og 200:
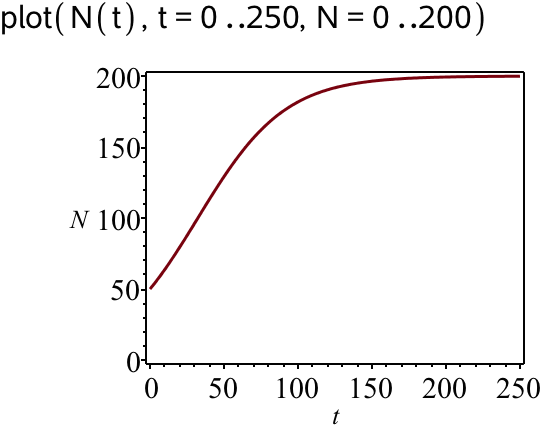
Ud fra grafen bedømmer man grænseværdien (toppen af figuren) til 200 kopper om dagen.
Opgave 15
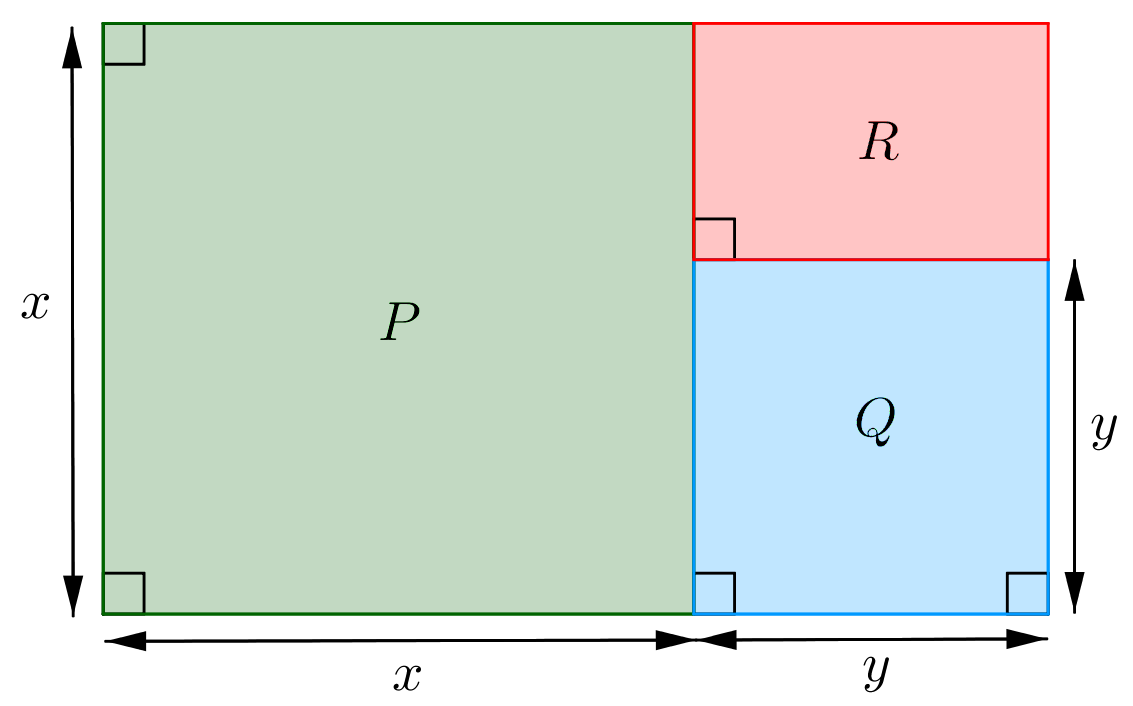
Et rektangulært område er opdelt i tre mindre områder P, Q og R, hvor P og Q er kvadrater med sidelængden henholdsvis x og y, og R er et rektangel (se figuren).
-
Opstil et udtryk for arealet af område R, udtrykt ved x og y.
-
Bestem x og y.
Det oplyses, at områdets bredde er 3/5 af længden, og at arealet af område R er 1800.
Svar på opgave 15 i Ti-Nspire:
-
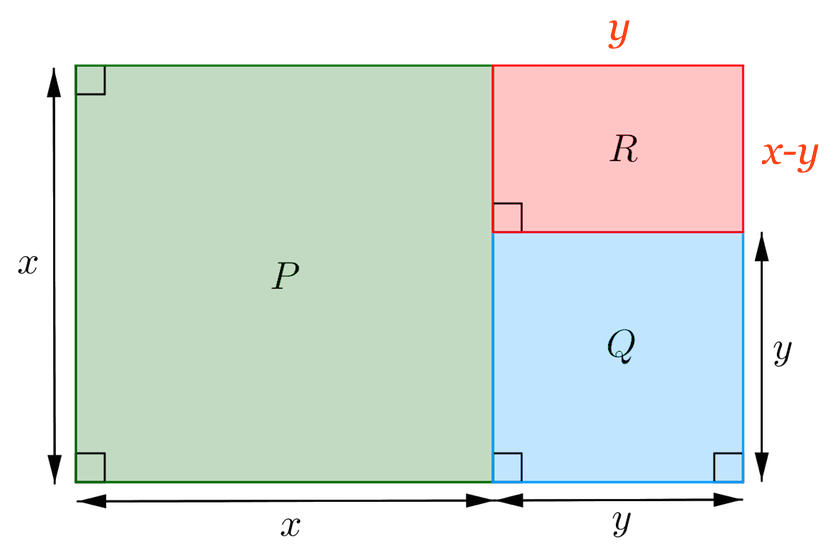
Den lodrette kant på R har længden (x - y) og den vandrette har længden y.
Dermed har R arealet y·(x - y)
-
Områdets bredde er x og dets længde er x + y. Dermed gælder, at x = (3/5)·(x+y). Arealet af R er y·(x - y), dvs. y·(x - y) = 1800. Disse to ligninger løses med hensyn til x og y:
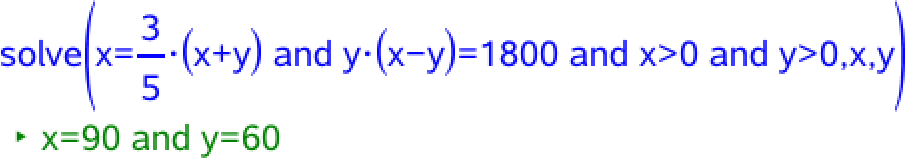
Dvs. x = 90 og y = 60
Svar på opgave 15 i Maple:
-
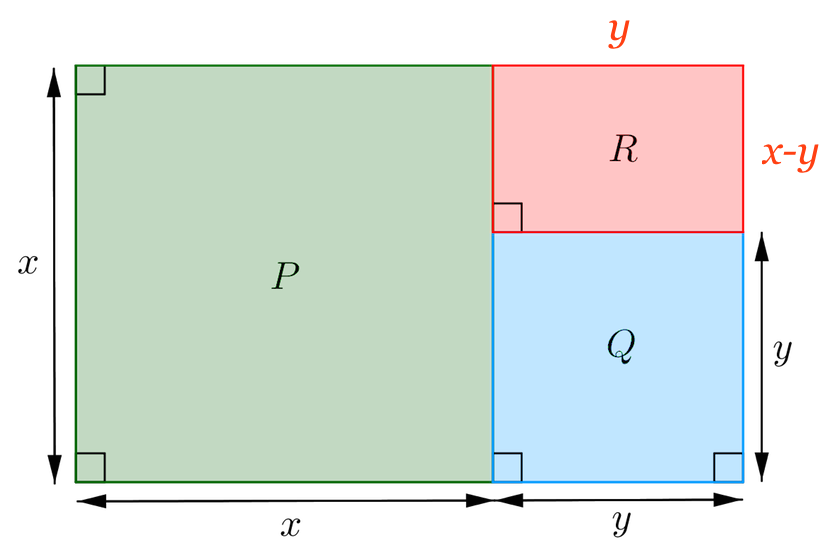
Den lodrette kant på R har længden (x - y) og den vandrette har længden y.
Dermed har R arealet y·(x - y)
-
Områdets bredde er x og dets længde er x + y. Dermed gælder, at x = (3/5)·(x+y). Arealet af R er y·(x - y), dvs. y·(x - y) = 1800. Disse to ligninger løses med hensyn til x og y:
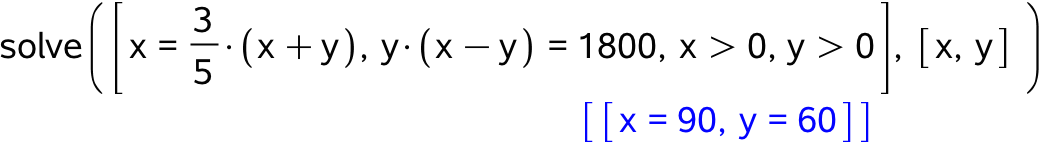
Dvs. x = 90 og y = 60