Svar på opgave 1:

1. A) svarer til g(x), da g(x) har negativ koefficient for x og dens graf dermed også en negativ hældning.

   B) svarer til f(x), da denne har positiv koefficient for x og dens graf dermed også en positiv hældning.

   C) svarer til h(x), da koefficienten til x er (usynligt lig) nul og hældningen af grafen dermed også er nul.

Svar på opgave 2:

1. Arealet af parallelogrammet er den numeriske værdi af determinaten til a og b.

   Determinanten er: (−1)·2 - 5·6 = −32.

   Dermed er arealet af parallelogrammet = 32

Svar på opgave 3:

1. Man finder nulpunkterne for f´(x) = x² + 2x - 3:

   x² + 2x - 3 = 0 ⇔

   x = -1 ± (1/2)·√[4 + 12] ⇔

   x = -1 ± 2 ⇔

   x = -3 ∨ x = 1

   For et tredjegradspolynomium f(x), hvor koefficienten for tredjegradsleddet er positiv, og hvor f´(x) har to nulpunkter, vil der gælde, at f(x) vokser før første nulpunkt for f´(x), aftager mellem de to nulpunkter for f´(x) og vokser igen efter andet nulpunkt for f´(x).

   Dvs. f vokser for x<-3, aftager for -3<x<1 og vokser for x>1

Svar på opgave 4:

1. Reducering:

   a² + 2ab - (a + b)² =

   a² + 2ab - (a² + 2ab + b²) =

   a² + 2ab - a² - 2ab - b² =

   (a² - a²) + (2ab - 2ab) - b² =

   −b²

   (x² + 2x)/(x + 2) =

   x·(x + 2)/(x + 2) =

   x

Svar på opgave 5:

1. Polynomiets toppunkt ligger midt mellem de to nulpunkter (2,0) og (4,0), dvs. x-værdien af toppunktet er (2+4)/2 = 3. Desuden er P'(x) = 0 i toppunktet, dvs. P'(3) = 0. Man får:

   P'(x) = 2ax + b ⇒ P'(3) = 2a·3 + b = 0 ⇔ b = -6a.

   Man ved, at P(2) = 0, da punktet (2,0) ligger på grafen for P. Dette giver sammen med b = -6a:

   P(2) = 0 ⇒ a·2² + (-6a)·2 + 4 = 0 ⇔ 4a - 12a + 4 = 0 ⇔ -8a = -4 ⇔ a = 1/2.

   Dette giver svaret: a = 1/2 og b = -6·(1/2) = -3

Svar på opgave 6:

1. For at beregne integralet, så bruger man substitutionen:

   u = x² + 1,

   du/dx = 2x ⇒ du = 2x·dx,

   u_start = 0²+1 = 1 og

   u_slut = 1²+1 = 2.

   Man får:

   

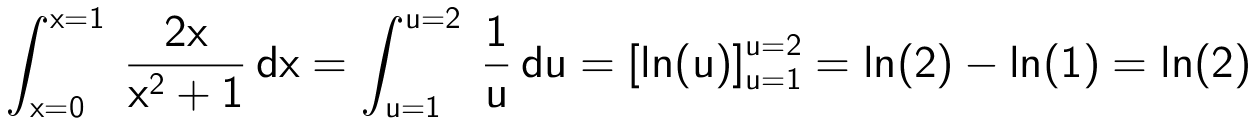
   Dvs. det bestemte integral er ln(2) = 0,693

Svar på opgave 7 i Ti-Nspire:

1. For at bestemme konstanterne a og b laver vi potensregression, da vi har fået angivet, at udviklingen kan beskrives ved y=bx^a. Vi opretter lister med nedslagsenergi og krafterradius.

   nedslagsenergi:={26,33,37,46,55,65} ▸ {26,33,37,46,55,65}

   kraterradius:={47,51,54,57,61,65} ▸ {47,51,54,57,61,65}

   Vi laver en potensregression, hvor resultatet gemmes i f1(x):

   

   Vi opskriver regressionsfunktionen:

   f1(x) ▸ 15.139*x^(0.348394)

   Heraf ses at a = 0,34839 og b = 15,139

2. For at bestemme nedslagsenergien, x, løses ligningen 48 = f1(x):

   solve(48=f1(x),x) ▸ x=27.4435

   Dvs. nedslagsenergien er 27,4 mJ

3. Lad x betegne start nedslagsenergien. Startværdien af kraterradius er f1(x). Slutværdien af kraterradius er f1(1.4*x). Den procentvise forskel på start og slut er:

   ((f1(1.4*x)-f1(x))/f1(x))*100 ▸ 12.4372

   Dvs. kraterradius øges med 12,4 %, når nedslagsenergien øges med 40 %.

   (Man kan også bruge formlen for procent-procent vækst: (1+r_y) = (1+r_x)^a ⇒ r_y = (1,4^0,348-1)·100% = 12,4 %.)

Svar på opgave 7 i Maple:

1. Man bruger gympakken til regression.

   with(Gym): ↵

   Man laver en potensregression på de to tabelrækker:

   PowReg([26, 33, 37, 46, 55, 65], [47, 51, 54, 57, 61, 65]) ↵

   

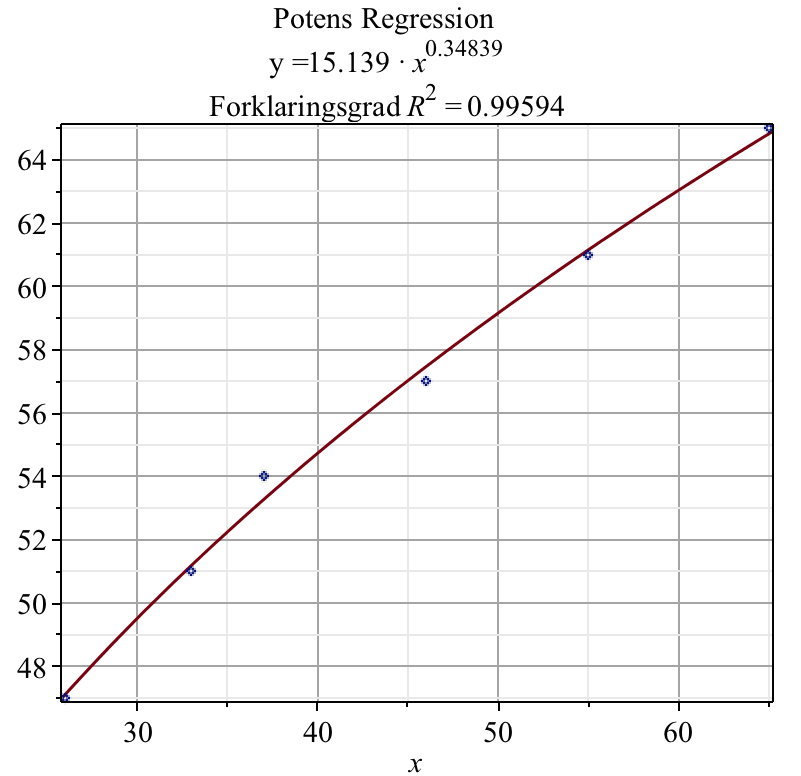
   Af anden linje på billedet ses, at a = 0,34839 og b = 15,139

2. For at bestemme nedslagsenergien, x, løses ligningen 15,139·x^0,34839 = 48 med hensyn til x:

   solve(15.139*x^0.34839 = 48, x) ↵ 27.44461

   Dvs. nedslagsenergien er 27,4 mJ

3. Man bruger formlen for procent-procent vækst: (1+r_y) = (1+r_x)^a ⇒ r_y = (1,4^0,348-1)·100% = 12,4 %.

   Dvs. kraterradius øges med 12,4 %, når nedslagsenergien øges med 40 %.

Svar på opgave 8 i Ti-Nspire:

1. Funktionen f oprettes:

   f(x):=x³-x²-4*x+4 ▸ Udført

   Grafen for f tegnes:

   

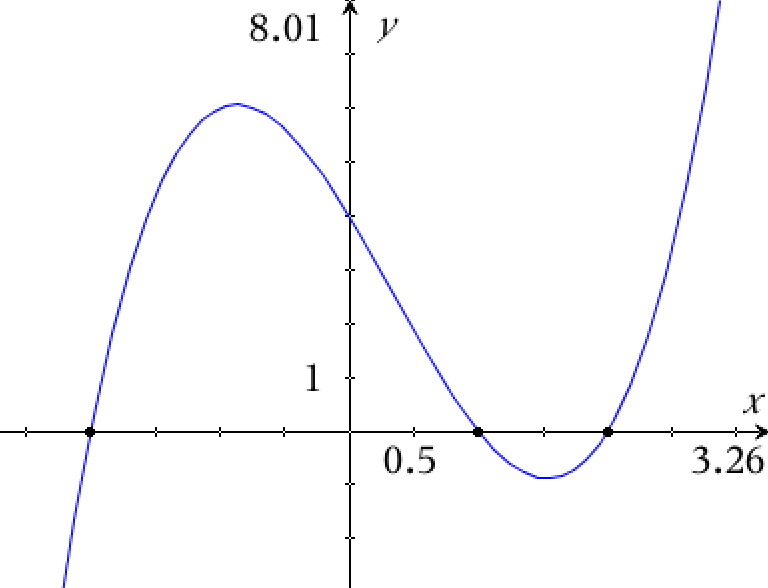
   Man bestemmer x-koordinaterne til nulpunkterne ved at løse ligningen f(x) = 0:

   solve(f(x)=0,x) ▸ x=−2 or x=1 or x=2

   Dvs. koordinatsættene til funktionens nulpunkter er: (-2,0), (1,0) og (2,0)

2. Ligningen til tangenten til grafen f i punktet P(3,f1(3)) har formlen: y = f´(x)·(x - 3) + f(3). Man har:

   f(3) ▸ 10

   derivative(f(x),x)|x=3 ▸ 17 (f´(3) = 17)

   Dette giver følgende ligningen for tangenten gennem P(3,f(3)): y = 17·(x - 3) + 10 ⇔ y = 17x - 41

   (Man kan også i Ti-nSpire bruge kommandoen tangentLine(): tangentLine(f1(x),x,3) ▸ y = 17x - 41)

Svar på opgave 8 i Maple:

1. (Gympakken er ikke nødvendig)

   Man opretter f(x):

   f := x³-x²-4*x+4 ↵ f := x → x³-x²-4*x+4

   Funktionen f plottes:

   plot(f(x), x = -3 .. 3) ↵

   

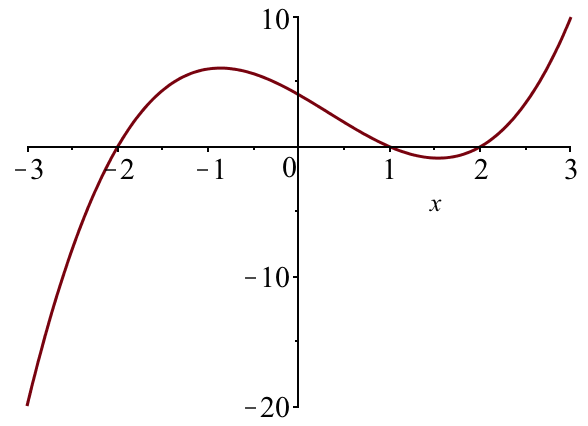
   Man bestemmer x-koordinaterne til nulpunkterne ved at løse ligningen f(x) = 0:

   solve(f(x) = 0, x) ↵ 1, 2, -2

   Dvs. koordinatsættene til funktionens nulpunkter er: (-2,0), (1,0) og (2,0)

2. Formlen for tangenten gennem P(3,f1(3)) er: y = f´(x)·(x - 3) + f(3). Man har:

   f'(3) ↵ 17

   f(3) ↵ 10

   Dvs. ligningen for tangenten gennem P(3,f(3)) er: y = 17·(x - 3) + 10 ⇔ y = 17x - 41

Svar på opgave 9 (uden CAS):

1. Arealet af trekant ABC kaldes T. Der gælder: T = (1/2)·|AB|·|AC|·sin(A)

   Da vi kender både |AB|, |AC| og arealet T, som er lig 3, og ved at ∠A er spids, skal vi løse ligningen: 30 = (1/2)·7·10·sin(∠A) med hensyn til ∠A og vælge den løsning, der ligger mellem 0 og 90°:

   30 = (1/2)·7·10·sin(∠A) ⇔ 30/35 = sin(∠A) ⇒ ∠A = sin^-1(6/7) = 58,9975°

   Dvs. ∠A = 59,0°

2. For at bestemme omkredsen af ABC, mangler vi at bestemme |BC|, som kan findes ved hjælp af en cosinusrelation:

   |BC|² = |AB|² + |AC|² - 2·|AB|·|AC|·cos(∠A) ⇒

   |BC| = √[7² + 10² - 2·7·10·cos(58,9973°)] = 8,76864

   Dvs. omkredsen af ABC er: 7 + 10 + 8,76864 = 25,8

Svar på opgave 10 i Ti-Nspire:

1. Nulhypotese: Artsfordeling er uafhængig af habitater

   Man laver en matrix (kaldet obs) med de observerede værdier:

   

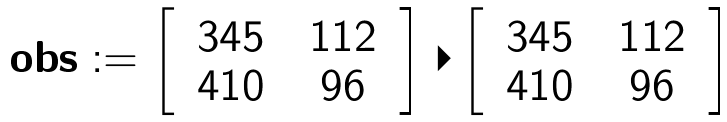
   Man laver en Chi-i-anden uafhængighedstest på matricen.

   χ²2way obs: stat.results ▸

   

   Det ses, at p-værdien (PVal) er 0,0371 = 3,71 %. Derfor forkastes nulhypotesen, da p-værdien er under signifikansniveauet på 5 %.

Svar på opgave 10 i Maple:

1. Man bruger gympakken til Chi-i-anden test.

   with(Gym): ↵

   Nulhypotese: Artsfordeling er uafhængig af habitater

   Man laver en matrix (kaldet obs) med de observerede værdier:

   

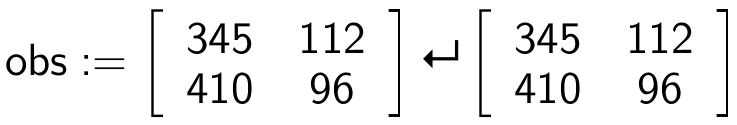
   Man laver en Chi-i-anden uafhængighedstest på matricen.

   ChiKvadratUtest(obs) ↵

   

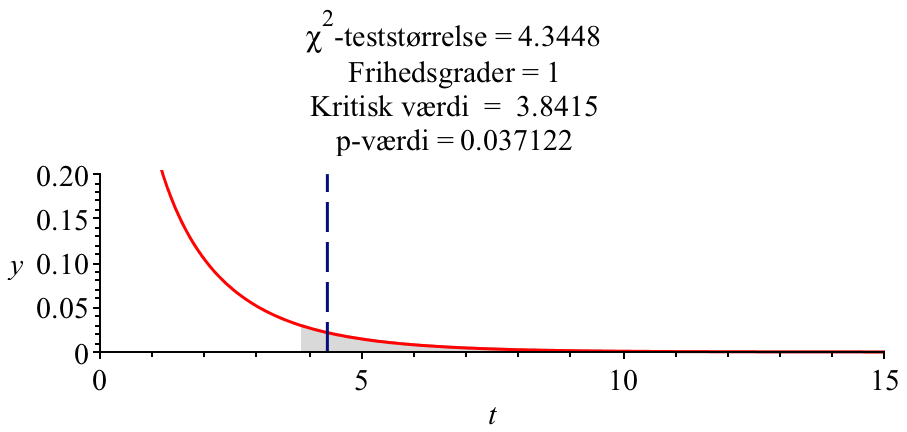
   Det ses i fjerde linje på billedet, at p-værdien er 0,0371 = 3,71 %. Dette er under signifikans­niveauet og derfor forkastes nulhypotesen.

Svar på opgave 11 i Ti-Nspire:

1. For at bestemme arealet af glasfladen OAB, defineres punkterne A og B som stedvektorer:

   a:=[14,0,24] ▸ [14,0,24]

   b:=[0,10,20] ▸ [0,10,20]

   Arealet af glasfladen kan bestemmes som halvdelen af længden af krydsproduktet (kaldet kryds) af vektorene OA og OB.

   kryds:=crossP(oa,ob) ▸ [−240,−280,140] (krydsproduktet af vektorerne OA og OB)

   norm(kryds)*1. ▸ 394.462 (længden af krydsproduktet)

   Dvs. arealet af glasfladen OAB er 0,5·394,462 dm² = 197,2 dm²

2. Vi ved, at parameterfremstillingen ser således ud: (x,y,z) = (x₀,y₀,z₀) + t·(r₁,r₂,r₃), hvor (x₀,y₀,z₀) er et punkt på linjen og (r₁,r₂,r₃) er en retningsvektor for linjen og t er et reelt tal.

   Linjens retningsvektor er OB = (0,10,20).

   Vi indsætter punket O = (0,0,0) og retningsvektoren OB i parameterfremstillingen og får:

   l: (x,y,z) = t·(0,10,20), t ∈ R

3. Den spidse vinkel mellem l og xy-planen er 90° - u, hvor u er vinklen mellem linjens retningsvektor og planens normalvektor. Vinklen u findes af formlen for vinklen mellem to vektorer:

   cos(u) = n·r/(|n|·|r|), hvor n er normalvektoren til planen og r er retningsvektoren for linjen l.

   Normalvektoren for xy-planen er (0,0,1). Retningsvektoren for linjen l er OB = [0,10,20]. Man får:

   u = cos^-1(n·r/(|n|·|r|)) = cos^-1((0,0,1)·(0,10,20)/(|(0,0,1)|·|(0,10,20)|)) = cos^-1(20/√500) = 26.565°.

   Den spidse vinklen mellem xy-planen og linjen l er derfor: 90° - 26,57° = 63,4°

Svar på opgave 11 i Maple:

1. Man bruger pakken "geom3d".

   with(geom3d): ↵

   Man opretter punkterne A og B (O behøver man ikke at oprette).

   point(A, 14, 0, 24) ↵ A

   point(B, 0, 10, 20) ↵ B

   Man opretter trekanten mellem punkterne O, A og B og kalder den T:

   triangle(T, [O, A, B]) ↵ T

   Man finder arealet af T:

   evalf(area(T)) ↵ 197.2308

   Dvs. arealet af glasfladen OAB er 197,2 dm²

2. Man opretter linjen l gennem punkterne O og B:

   line(l, [O, B]) ↵ l

   Man finder parameterfremstillingen for l:

   Equation(l) ↵ [0, 10 t, 20 t]

   Dvs. l: (x,y,z) = t·(0,10,20), t ∈ R

3. Man opretter xy-planen (kaldet xy) gennem punktet O og med normalvektoren (0,0,1), der er basisvektor for z-aksen.

   plane(xy, [O, [0, 0, 1]]) ↵ xy

   Man finder vinklen mellem i og xy-planen som decimaltal i radianer:

   evalf(FindAngle(l, xy)) ↵ 1.107149

   Dette omregnes til grader:

   (1.107148717*180)/π ↵ 63.43495

   Den spidse vinklen mellem xy-planen og linjen l er derfor: 63,4°

Svar på opgave 12 i Ti-Nspire:

1. Begge sider af differentialligningen angiver ændringen i temperatur pr. tidsenhed.

   For at bestemme temperaturens væksthastighed, når temperaturen i akvariet er 26°C, så indsættes T = 26 i differentialligningen:

   dT/dx = 1,54 - 0,259·(26-22) °C/time = 0,504 °C/time

2. For at bestemme hvor lang tid, der går før T = 27 nås, løses differentialligningen med hensyn til T(x):

   deSolve(t'=1.54-0.259*(t-22) and t(0)=22,x,t) ▸ t=27.9459-5.94595*(0.771823)^x

   Løsningen oprettes som funktion.

   t(x):=27.9459-5.94595*(0.771823)^x ▸ Udført

   Man løser ligningen T(x) = 27, med hensyn til x:

   solve(27=t(x),x) ▸ x=7.09779

   Dvs. fisken kan slippes ned i akvariet efter 7,1 time

Svar på opgave 12 i Maple:

1. Begge sider af differentialligningen angiver ændringen i temperatur pr. tidsenhed.

   For at bestemme temperaturens væksthastighed, når temperaturen i akvariet er 26°C, så indsættes T = 26 i differentialligningen:

   dT/dx = 1,54 - 0,259·(26-22) °C/time = 0,504 °C/time

2. For at bestemme hvor lang tid, der går før T = 27 °C nås, løses differentialligningen med hensyn til T(x). Man bruger evalf(desolve()) for at få resultatet som decimaltal.

   evalf(dsolve([T(0) = 22, T'(x) = 1.54-.259*(T(x)-22)])) ↵

      T(x) = 27.94595 - 5.945946*exp(-0.2590000 x)

   Man løser ligningen T(x) = 27, med hensyn til x:

   fsolve(27.94595-5.945946*exp(-.2590000*x) = 27) ↵ 7.097604

   Dvs. fisken kan slippes ned i akvariet efter 7,1 time

Svar på opgave 13 i Ti-Nspire:

1. Man opretter f(x) og g(x):

   f(x):=2*(0.5)^x ▸ Udført

   g(x):=4 ▸ Udført

   Arealet af M kan bestemmes ved at finde det bestemte integral af f(x)-g(x) mellem x-værdien til skæringspunktet mellem f(x) og g(x) og x=0:

   solve(f(x)=g(x),x) ▸ x=−1.

   Skæringspunktets x-værdi indsættes i det bestemte integral:

   integral(g(x)-f(x),x,−1,0) ▸ 1.11461

   Dvs. arealet af punktmængden M er 1,115

2. For at finde k skal man løse følgende ligning med hensyn til k:

   

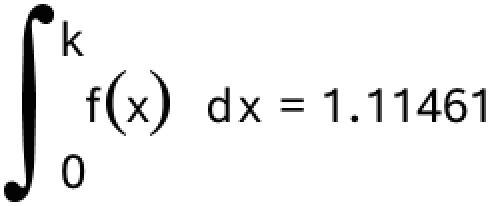
   Man får:

   solve(integral(f(x),x,0,k)=1.11461,k) ▸ k=0.704381

   Dvs., når k = 0,704, er arealerne af M og N lige store.

Svar på opgave 13 i Maple:

1. Man opretter f(x) og g(x):

   f := 2*.5^x ↵ x → 2 0.5^x

   g := 4 ↵ x → 4

   Arealet af M kan bestemmes ved at finde det bestemte integral af f(x)-g(x) mellem x-værdien til skæringspunktet mellem f(x) og g(x) og x=0:

   solve(f(x) = g(x)) ↵ -1.

   Skæringspunktets x-værdi indsættes i det bestemte integral:

   int(g(x)-f(x), x = -1 .. 0) ↵ 1.114610

   Dvs. arealet af punktmængden M er 1,115

2. Man skal finde det k, der gør at integralet af f(x) fra x=0 til x=k er lig med 1,114610. Man får:

   solve(1.114610 = int(f(x), x = 0 .. k), k) ↵ 0.7043813

   Dvs., når k = 0,704, er arealerne af M og N lige store.

Svar på opgave 14 i Ti-Nspire:

1. Udviklingen er: y = b*a^t, hvor t er antal år efter 1980 og y er antal rygere i mio.

   Man skal finde a og b. Man ved, at y = 721 for t = 0. Dette giver b:

   721 = b·a⁰ ⇒ b = 721.

   Tallet a findes for året 2012, der svarer til t = (2012-1980) = 32. Her er y = 967. Man får:

   967 = 721·a³² ⇒ a = ³²√[967/721] = 1,00922.

   Dvs. y(t) = 721·1,00922^t

2. Man opretter y(t):

   y(t):=721.*1.00922^t ▸ Udført

   Man opretter N(t):

   n(t):=(12245./(1+1.74*exp(−0.0273*t)) ▸ Udført

   Man opretter en funktionen g(t) = y(t)/N(t), som angiver andelen af rygere af verdens befolkning:

   g(t):=y(t)/n(t) ▸ Udført

   Man udskriver g(t):

   g(t) ▸ 0.058881*0.982041^t*(1.02768^t+1.74)

   Dvs. g(t) = 0,058881·0,982041^t·(1,02768^t + 1,74)

   Man bruger kommandoen fMin() for at finde det t, der giver minimum: fMin(g(t),t)|t>0 ▸ t=45.2104

   Dette svarer til år 1980 + 45 = 2025

Svar på opgave 14 i Maple:

1. Udviklingen er: y = b*a^t, hvor t er antal år efter 1980 og y er antal rygere i mio.

   Man skal finde a og b. Man ved, at y = 721 for t = 0. Dette giver b:

   721 = b·a⁰ ⇒ b = 721.

   Tallet a findes for året 2012, der svarer til t = (2012-1980) = 32. Her er y = 967. Man får:

   967 = 721·a³² ⇒ a = ³²√[967/721] = 1,00922.

   Dvs. y(t) = 721·1.00922^t

2. Man opretter y(t):

   y := 721*1.009216^t ↵ t → 721*1.009216^t

   Man opretter N(t):

   N := 12245/(1+1.74*exp(-0.0273*t)) ↵ N:= t → 12245/(1+1.74*exp(-0.0273*t))

   Man opretter en funktionen g(t) = y(t)/N(t), som angiver andelen af rygere af verdens befolkning:

   g:= y(t)/N(t) ↵ t → y(t)/N(t)

   Man udskriver g(t):

   evalf(g(t)) ↵ t → 0.058881*1.009216^t*(1+1.74*exp(-0.0273*t))

   Dvs. g(t) = 0,058881·1,009216^t·(1+1,74·exp(-0,0273*t))

   Man bruger minimize() kommandoen:

   minimize(g, t = 0 .. infinity, location) ↵ 0.13429, {[{t = 45.234}, 0.13429]}

   Dette viser, at andelen af rygere ud af verdens befolkning når sin minimum for t=45,2, dvs. i år 1980 + 45 = 2025

   Kontrol af afrunding: g(45) ↵ 0.134292 og g(46) ↵ 0.134298. Dvs. t=45 giver den mindste værdi, når t er et helt tal.

Svar på opgave 15 (uden CAS):

1. ACF og ABG er ligebenede trekanter, hvor topvinklen er 33° i dem begge. For en ligebenet trekant gælder, at grundlinje = 2·benlængde·cos(grundvinkel).

   Grundvinklen er (180° - topvinkel)/2 = (180° - 33°)/2 = 73,5°. Dette giver:

   |AF| = 2·340·cos(73,5°) = 193,13 og

   |AG| = 2·210·cos(73,5°) = 119,29.

   Dvs. |AF|/|AG| = 193,13/119,29 = 1,62, som er lig med det gyldne snit med to decimalers nøjagtighed.

2. Da trekant ACF og trekant ABG er ensvinklede, så gælder, at |AF|/|AG| = |AC|/|AB| = 340/210 = 1,62, der er lig med det gyldne snit med to decimalers nøjagtighed.