Svar på opgave 1:

1. (x + 5)² - 25 = x² + 10x + 25 - 25 = x² + 10x

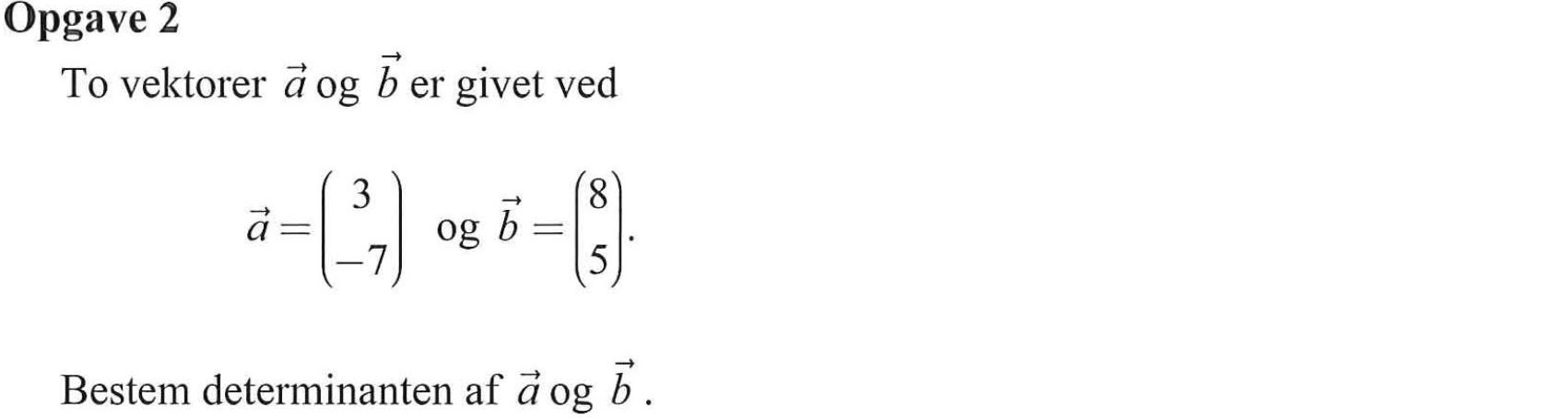
Svar på opgave 2:

1. det(a,b) = 3·5 - (-7)·8 = 15 + 56 = 71

Svar på opgave 3:

1. x er år efter 2010, mens f(x) er indtægter i mio. kr.

   Den årlige fremskrivningsfaktor er 1,118 og startværdien er 15.

   Man får modellen: f(x) = 15·1,118^x, x > 0

Svar på opgave 4:

1. En vilkårlig stamfunktion F til f har formen F(x) = (1/4)·x⁴ + 5·x² + k.

   Man skal bestemme k, så F(2) = 20 ⇒ (1/4)·2⁴ + 5·2² + k = 20 ⇒ k = -4.

   Dermed bliver stamfunktionen (¼)·x⁴ + 5·x² - 4

Svar på opgave 5:

1. Man skal indsætte f(x) og f´(x) i ligningen for at gøre prøve. Man får f´(x) = 5·e^x + 1. Indsat i differentialligningen får man:

   Venstre side: 5·e^x + 1

   Højre side: 5·e^x + x - x + 1 = 5·e^x + 1

   Da venstre og højre side giver det samme, stemmer prøven, og f(x) er dermed en løsning til differentialligningen.

Svar på opgave 6:

1. Begge parabler går gennem (-2,0) og (6,0) der ud fra nulreglen ses at være rødder i begge polynomier. De vender begge grenene opad, da både k og m er positive. Da k > m har f et lavere toppunkt end g og mere samlede grene.

   Tegning i Geogebra:

   

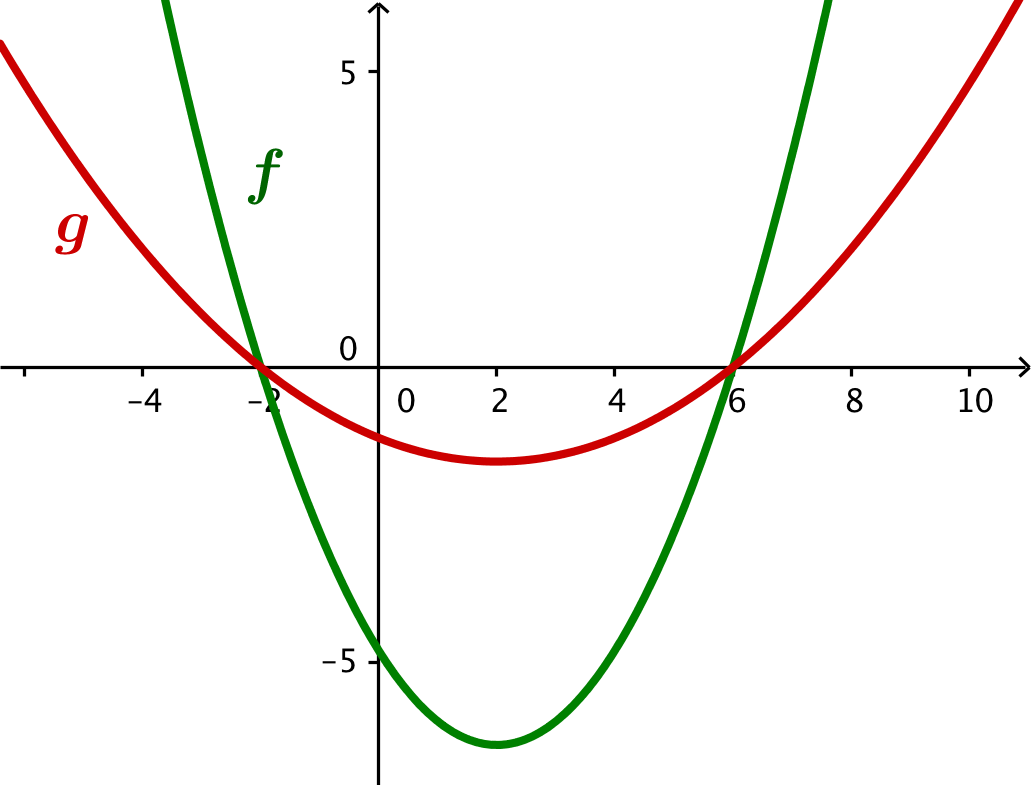
Svar på opgave 7:

1. I Ti-Nspire laver man en liste med x, hvor x er antal år efter 2000:

   x:={0,2,4,6,8,10,12,14} ▸ {0,2,4,6,8,10,12,14}

   Tilsvarende laver man en liste med gennemsnitlig levealder:

   alder:={74.3,74.7,75.2,75.9,76.3,77.1,77.9,78.5} ▸ {74.3,74.7,75.2,75.9,76.3,77.1,77.9,78.5}

   Man vælger kommandoen:

   Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Lineær regression (mx + b)...

   Derefter vælger man de to lister og får resultatet:

   

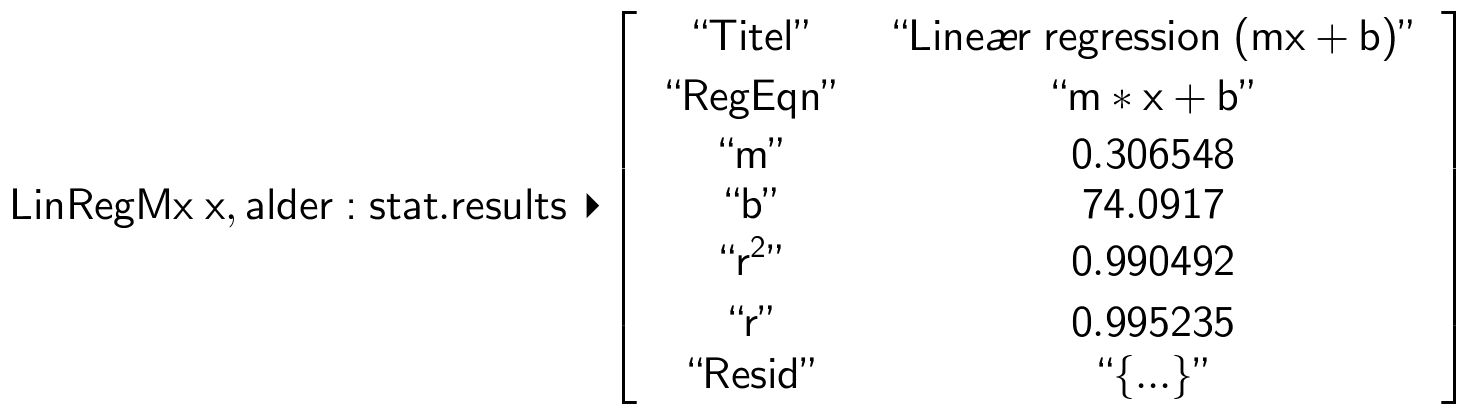
   Forskriften for f(x) bliver: f(x) = 0,31x + 74,1

2. 0,26 er det antal år som gennemsnitslevealderen stiger med hvert år for kvinder, og 79 er den gennemsnitlige levealder for kvinder i 2000.

3. Løsning i Ti-Nspire: Man definerer først f(x) og g(x):

   f(x):=0.31*x+74.1 ▸ Udført

   g(x):=0.26*x+79 ▸ Udført

   Dernæst findes det antal år, der går før kvinders gennemsnitslevealder er 81 år:

   solve(g(x)=81,x) ▸ x=7.69

   Dette tal sættes ind i forskriften for f:

   f(7.69) ▸ 76.5

   Dermed er mænds gennemsnitslevealder 76,5 år, når kvinders er 81 år.

Svar på opgave 8:

1. Grafen for f er tegnet i Geogebra:

   

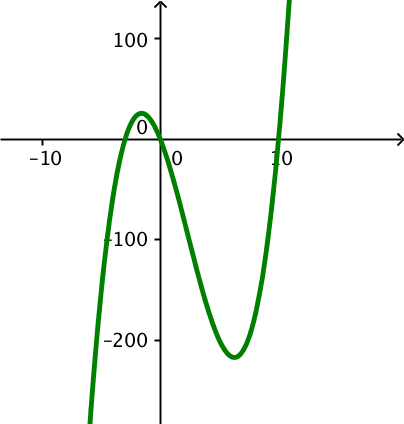
   Nulpunkter for f findes i Ti-Nspire:

   solve(x³-7*x²-30*x=0,x) ▸ x=−3 or x=0 or x=10

   Dvs. nulpunkterne er x = −3 ∨ x = 0 ∨ x = 10

2. Man bruger Ti-Nspire kommandoen: y=tangentLine(x³-7*x²-30*x,x,3) ▸ y=9-45*x

   Dvs. tangentligningen er y = -45x + 9

3. Man skal finde de intervaller hvor f´(x) < 0, og hvor f´(x) > 0 . Dette gøres i Ti-Nspire:

   solve(3*x²-14*x-30 < 0.,x) ▸ −1.59661 < x < 6.26328

   solve(3*x²-14*x-30 > 0.,x) ▸ x < −1.59661 or x > 6.26328

   Dvs. f(x) vokser for x kommende fra minus uendelig og gående mod -1,60, aftager derefter for x liggende mellem -1,60 og 6,26 og vokser til sidst for x større end 6,26

Svar på opgave 9:

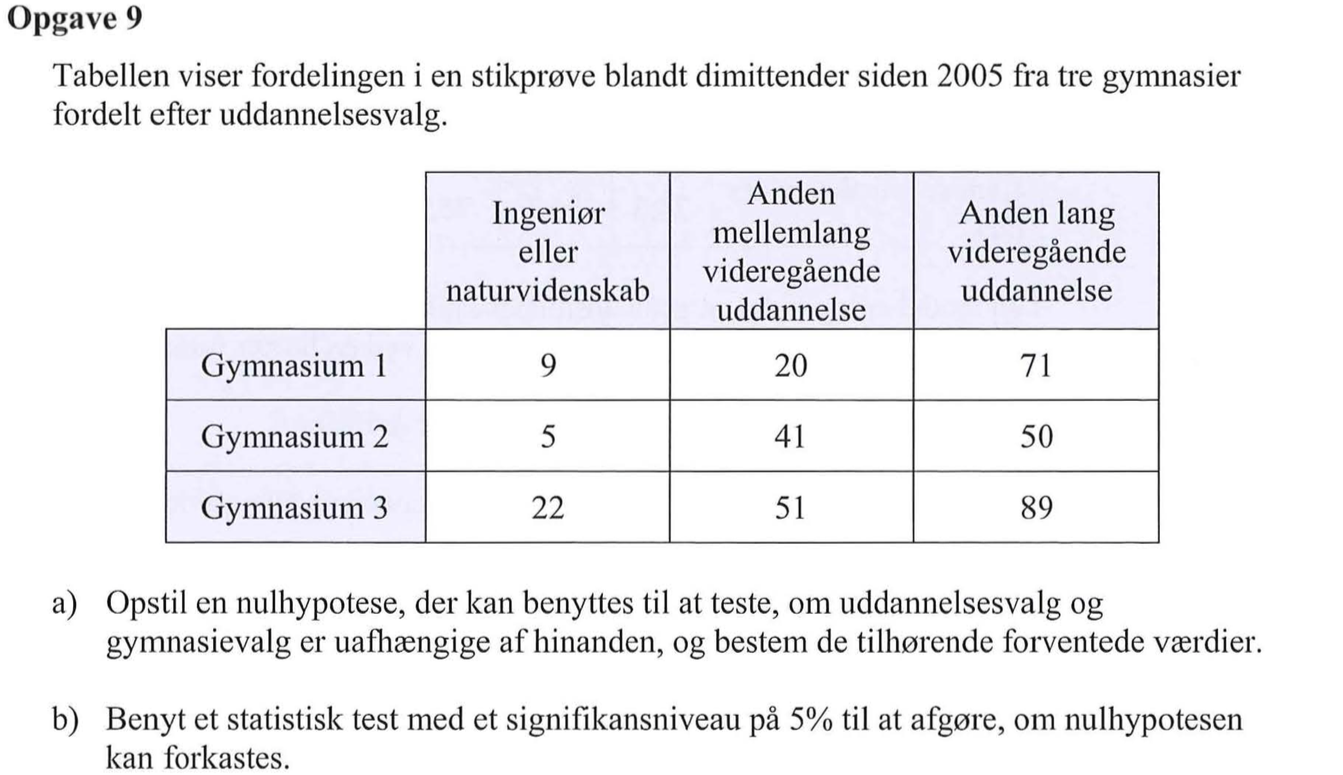
1. Nulhypotesen er, at uddannelsesvalg er uafhængigt af valg af gymnasium

   Man opretter en matrix med de observerede værdier i Ti-Nspire.

   

   Man vælger kommandoen: Beregninger ▸ Statistik ▸ Statistiske tests ▸ χ²-uafhængighedstest og matricen observeret, som man lige har oprettet. Det giver:

   

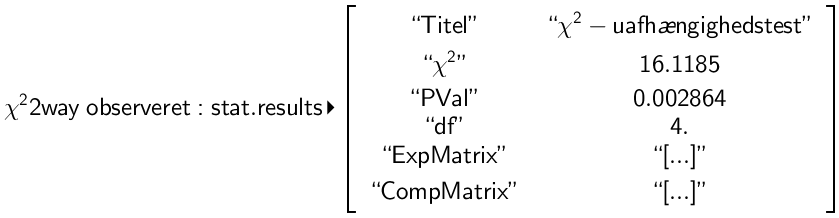
   Dernæst finder man de forventede værdier med kommandoen:

   

2. Man aflæser PVal = 0,00286 = 0,3 % ovenfor. Da den er mindre end 5% forkastes nulhypotesen.

Svar på opgave 10 (potentiel energi for Argonatomer):

1. Man definerer U(r) i Ti-Nspire:

   

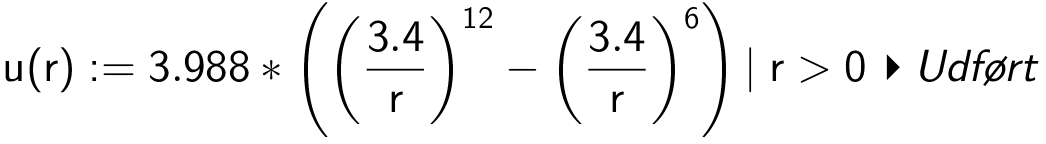
   Herfra beregnes U(3,4) i Ti-Nspire: u(3.4) ▸ 0

   Tegning i Geogebra:

   

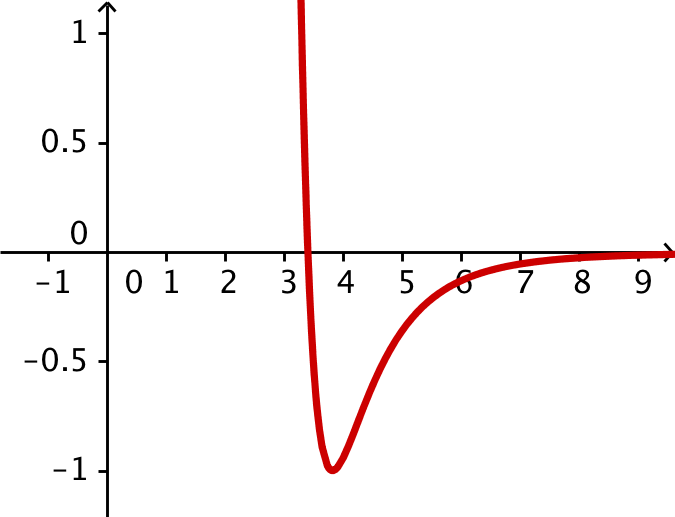
2. Man finder minimum for den potentielle energi i Ti-Nspire ved hælp af fMin() kommandoen:

   fMin(u(r),r)|r>0 ▸ r=3.816

   Minimumsværdien for U(r) er u(3.8164) ▸ −0,997

   Alternativ løsning: Man kan bestemme minimumspunktet for den potentielle energi ved at finde nulpunkter for U'(r).

   U'(r) = 36964,1·(r⁶ - 3089,61)/r¹³. Det ses, at U'(r) = 0 ⇒ (r⁶ - 3089,61) = 0 ⇒ r = 3,81637. Dette indsættes i U(r) og man får samme minimumsværdi som ovenfor.

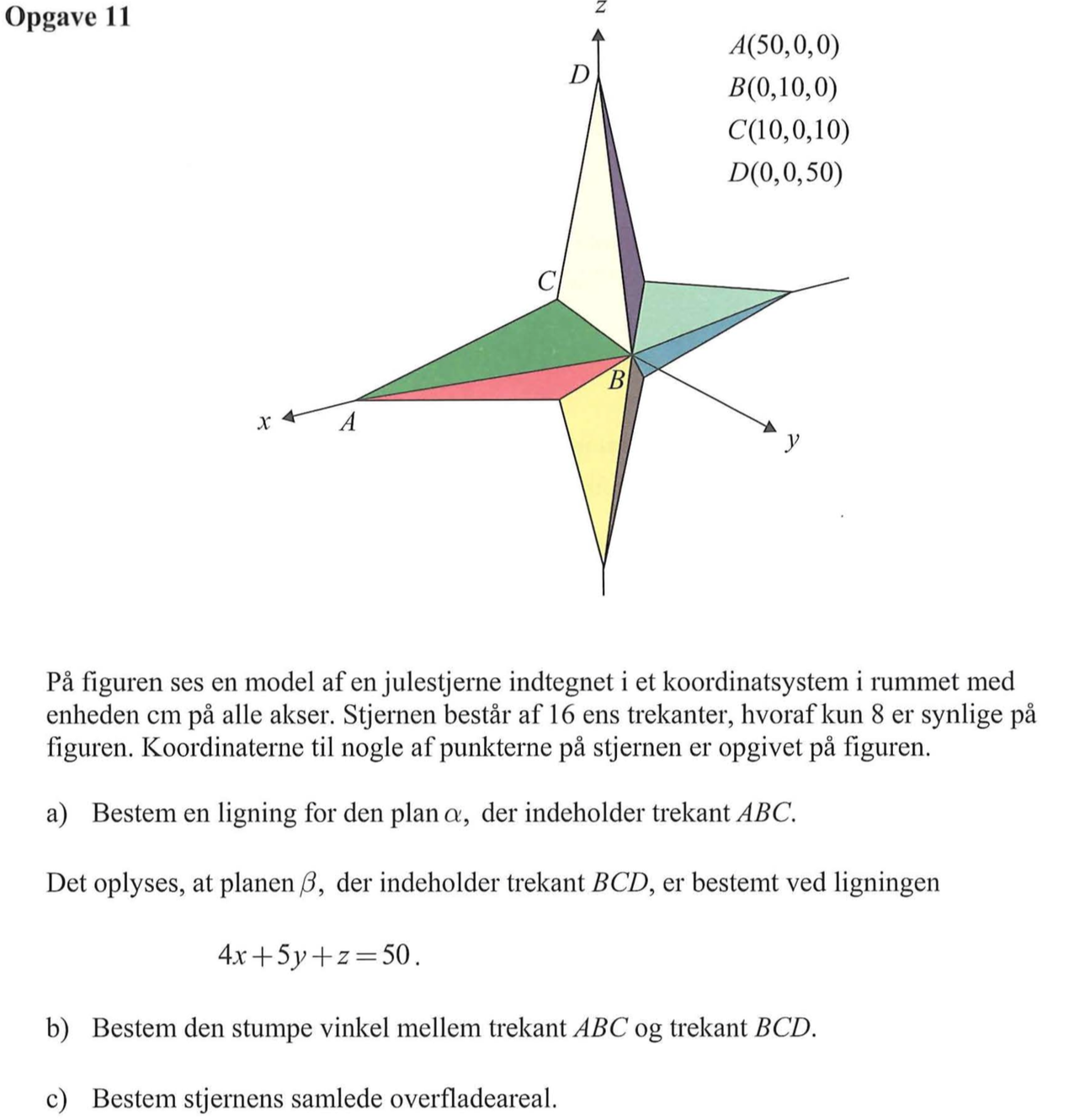
Svar på opgave 11:

Løsning i Geogebra:

1. Punkterne A-D indsættes ved hjælp af input-feltet. Derefter bruges Flade Gennem Tre Punkter-værktøjet til at oprette α, der er vist med rødt.

   Ligningen for α aflæses og omskrives til x + 5y + 4z - 50 = 0

2. Planen β, som er blå på tegningen, oprettes ved at skrive β's ligning i inputfeltet. Ved hjælp af vinkel-værktøjet findes den stumpe vinkel mellem α og β til 141,8°

   Bemærk: vinkel-værktøjet kan både give den spidse og den stumpe vinkel mellem to planer. Hvilken én, som man får, afhænger af den rækkefølge, som man bruger, når man opretter α. Rækkefølgen A-B-C giver den spidse vinkel, mens rækkefølgen A-C-B giver den stumpe.

3. Man finder arealet af ABC ved at tegne trekant ABC med polygon-værktøjet. Trekanten er vist med grønt og dens areal aflæses til 324,0. Stjernens overfladeareal bliver 16·324,0 = 5.184,6

Løsning i Ti-Nspire.

1. Man starter med at definere punkterne A-C som vektorer (D er ikke nødvendigt).

   a:=[50,0,0] ▸ [50,0,0]

   b:=[0,10,0] ▸ [0,10,0]

   c:=[10,0,10] ▸ [10,0,10]

   Planen har normalvektoren ABxAC = crossP(b-a,c-a) ▸ [100,500,400]. Denne forenkles ved at dividere igennem med mindste koordinat: [1,5,4]. En vektor fra A til et punkt i planen står vinkelret på normalvelktoren, hvilket giver ligningen:

   dotP([1,5,4],[50-x,0-y,0-z])=0 ▸ −x-5*y-4*z+50=0, hvilket giver planen α's ligning:

   x + 5y + 4z - 50 = 0

2. β's normalvektor af læses af koefficienterne i dens ligning til (4,5,1). Det samme med α's. Den stumpe vinkel, x, mellem α og β findes som den største vinkel mellem deres normalvektorer :

   

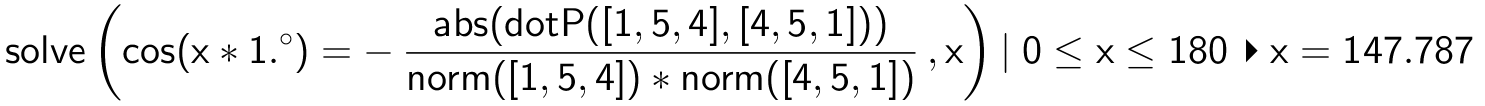
   Dvs. den stumpe vinkel mellem α og β er 141,8°

3. Stjernen består af 16 ens trekanter, der hver har et areal, der er halvdelen af længden af krydsproduktet ABxAC, dvs. 0.5*norm([100,500,400]) ▸ 324.037. Dette giver den samlede overfadeareal for stjernen: 16*324.037 ▸ 5.184,6

Svar på opgave 12:

Løsning i Geogebra.

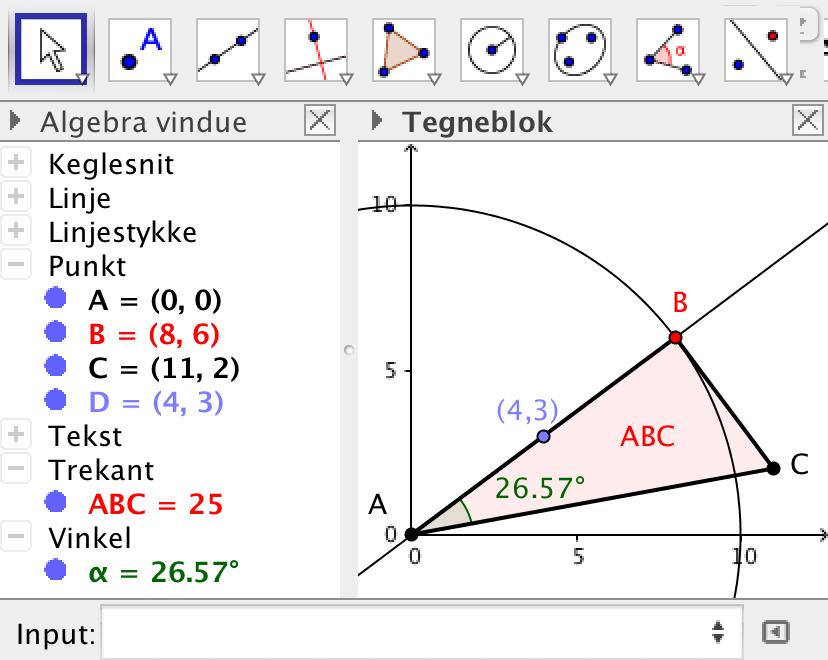
1. Punkterne A og C oprettes i input-feltet. Hjælpepunktet D = (4,3) indføres til støtte for oprettelse af linjen l. D svarer til punktet for t = 1 på l. Punktet A svarer til t = 0.

   Linjen l konstrueres ved hjælp af linje-værktøjet ud fra A og D. En cirkel med centrum i A og radius = 10 konstrueres ved hjælp af "Cirkel ud fra centrum og radius"-værktøjet. Cirklens skæring med l i første kvadrant er punktet B.

   A, B og C forbindes med polygon-værktøjet. Vinkel A findes til 26,6° ved hjælp af vinkel-værktøjet.

2. Koordinaterne til B aflæses til (8,6) og arealet af ABC til 25

Løsning i Ti-Nspire.

1. Man skal finde vinklen mellen vektor AC og retningsvektoren for linjen l:

   

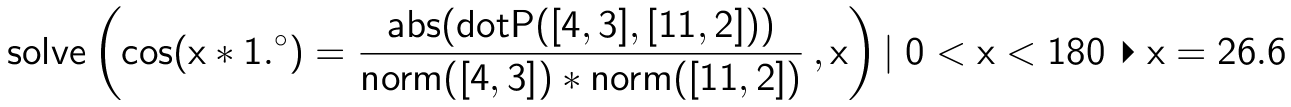
   Dette bliver 26,6°

2. Retningsvektoren for linjen er r = (4,3). Vektoren AB = c·(4,3), hvor c er en konstant.

   Man skal bestemme c, |AB| = 10. Dvs. man skal løse følgende ligning med hensyn til c:

   |c·(4,3)| = 10 ⇔

   |c·(4,3)|² = 100 ⇔

   (4·c)² + (3·c)² = 100 ⇔

   (16 + 9)·c² = 100 ⇔

   25·c² = 100 ⇔

   c² = 4 ⇒

   c = 2

   Dernæst indsættes c: AB = 2·(4,3) = (8,6).

   Dvs. B = (8,6)

   Arealet af den trekant, der udspændes af to vektorer, er halvdelen af den numeriske værdi af determinaten af vektorerne.

   AB = (8,6) og AC = (11,2).

   Dvs. arealet af trekant ABC er: 0,5·|det((8,6),(11,2))| = 0,5·|8·2 - 6·11| = 25

Svar på opgave 13:

1. Man løser differentialligningen i Ti-Nspire:

   deSolve(n'=0.01*sin(0.017*t-1.03)*n and n(0)=100,t,n)|0≤t≤365 ▸

   0≤t≤365 and n=135.369*(0.555306)^{cos(0.017*t-1.03)}

   Dvs. N(t) = 135,4·0,555^{cos(0,017·t - 1,03)} mio. stk., 0 ≤ t ≤ 365 døgn

   Tegnet i Geogebra:

   

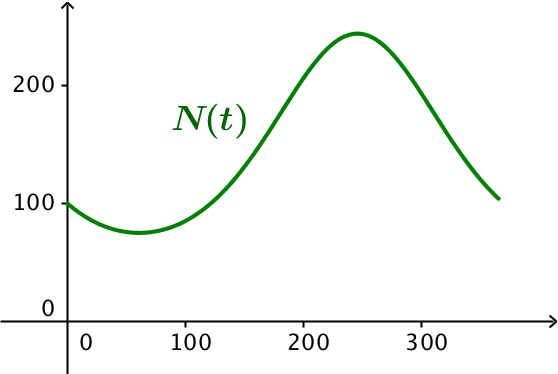
2. Man skal finde den t-værdi, der hører til den største værdi af N'(t) i intervallet 0 ≤ t ≤ 365. Man bruger fMax() kommandoen kombineret med kommandoen derivative() (dvs. afledet funktion) i Ti-Nspire:

   fMax(derivative(135.369*0.555306^{cos(0.017*t-1.03)},t),t)|0≤t≤365 ▸ t=181.267

   Dette viser, at den største væksthastighed findes for t = 181 døgn

Svar på opgave 14:

1. f(x) defineres i Ti-Nspire: f(x):=a*sqrt(x*(16-x))| 0 ≤ x ≤ 10 ▸ Udført

   Konstanten a findes med kommandoen

   

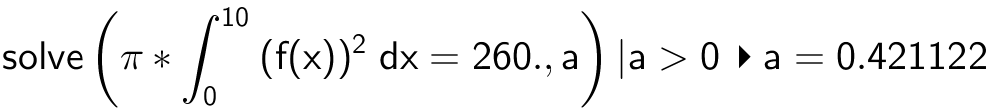
   Værdien af a bliver 0,42

2. Markeringen kaldes b og findes med kommandoen

   

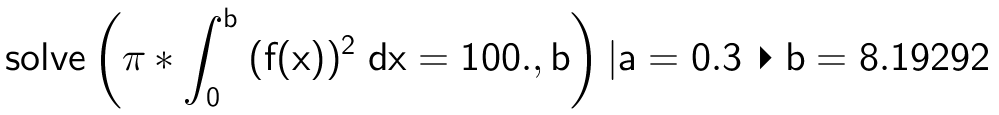
   Dvs. markeringen skal anbrínges ved 8,19