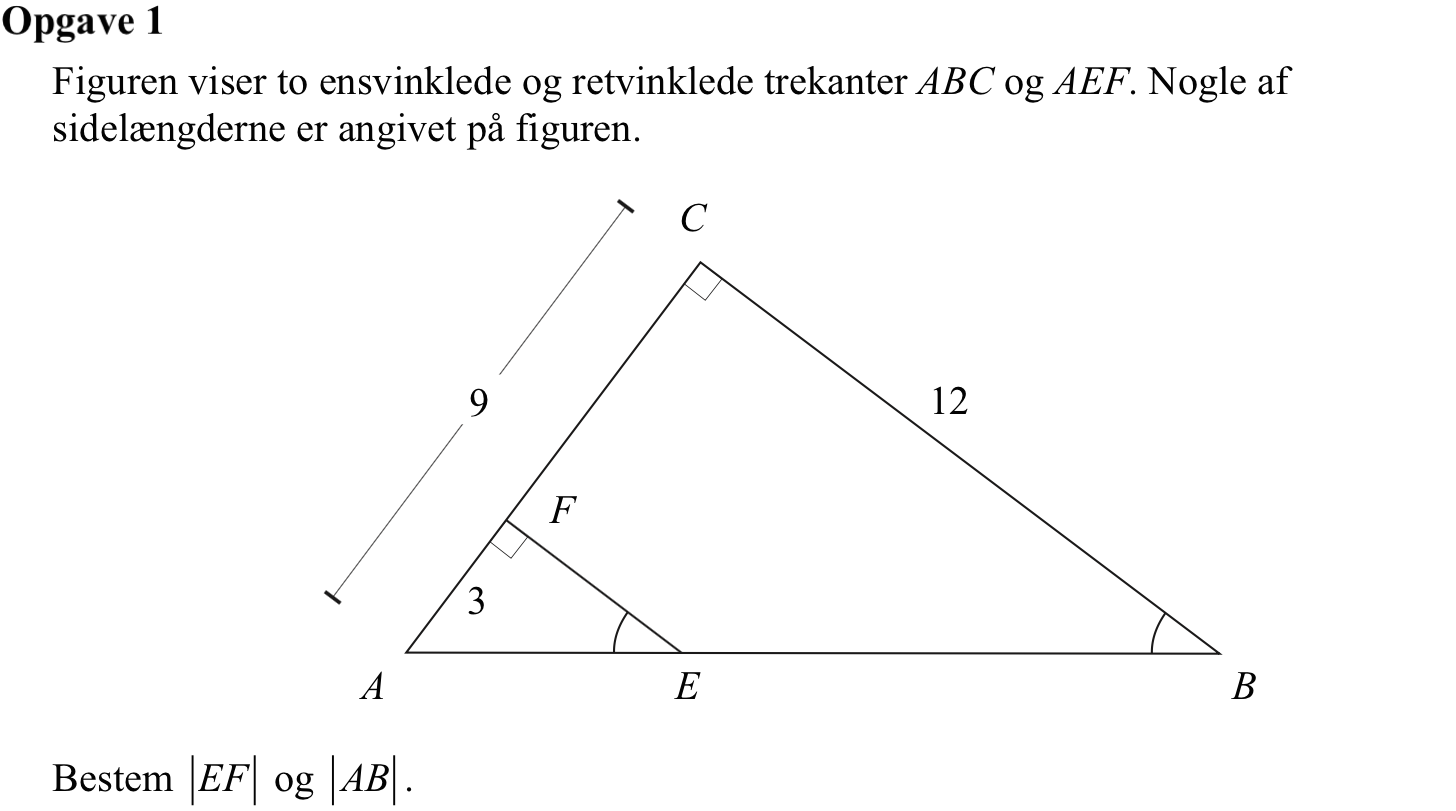
Svar på opgave 1:

1. Skaleringsfaktoren er 9/3 = 3. Dvs. |EF| = 12/3 = 4.

   |AB| findes ved hjælp af Pythagoras læresætning: |AB| = √[12² + 9²] = 15

Svar på opgave 2:

1. 3x + y -11 = 0 ∧ 2x - 3y + 11 = 0 ⇒

   y = -3x + 11 ∧ 2x - 3·(-3x + 11) + 11 = 0 ⇒

   y = -3x + 11 ∧ 2x + 9x - 33 + 11 = 0 ⇒

   y = -3x + 11 ∧ 11x - 22 = 0 ⇒

   y = -3·(2) + 11 ∧ x = 2 ⇒

   x = 2 ∧ y = 5

Svar på opgave 3:

1. Tangentens ligning: y = f´(3)·(x - 3) + f(3).

   Her findes f´(3) ved at indsætte x = 3 og y = 5 i højre side af differentialligningen, og man får: 5·(3 - 1) = 10, hvilket indsat giver tangentens ligning:

   y = 10x - 25

Svar på opgave 4:

1. Der er tale om en aftagende eksponentiel udvikling. x = antal år efter 2004, f(x) er antallet af myg. Startværdien er 5.382.

   f(x) = 5.382·(1 - 70%)^x = 5.382·0,30^x

Svar på opgave 5:

1. Man skal undersøge om f´(x) = g(x). Hvis det er tilfældet, er f(x) en stamfunktion til g(x).

   f´(x) = 2·ln(x) + (2x + 1)·(1/x) = 2·ln(x) + 2 + (1/x) ≠ g(x).

   Dermed er f(x) ikke stamfunktion til g(x)

Svar på opgave 6:

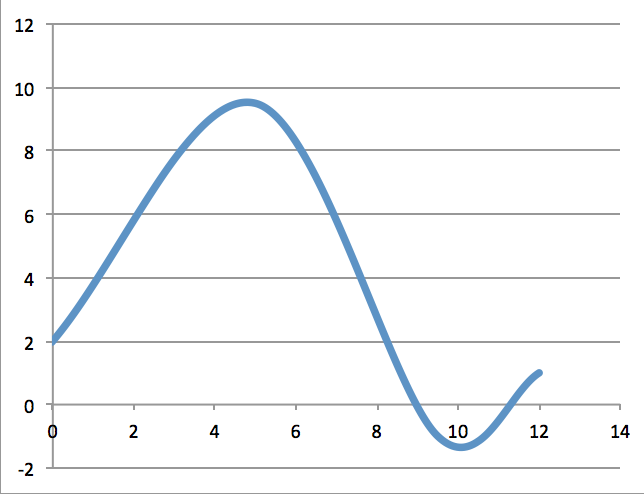
1. Funktionen vokser hele vejen for x gående fra minus-uendelig til x = 5. På vejen skærer den y-aksen i y = 2. For x = 5 har den et lokalt maksimum for derefter at falde til x = 10, hvor den har lokalt minimum. Den vokser derefter igen for x gående mod uendelig og antager undervejs y-værdien 1 for x = 12.

   Nedenstående graf er lavet i Excel ud fra 4 punkter som punktdiagram med jævne kurver:

   

Svar på opgave 7:

1. Man indfører variablen t = (2011 - årstal). Man opretter følgende lister for t og omsætning i Ti-Nspire:

   t:={0,1,2,3} ▸ {0,1,2,3} og omsaetning:={0.3,0.8,1.6,4.9} ▸ {0.3,0.8,1.6,4.9}

   Man vælger kommandoen Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression... ▸ listerne "t" og "omsaetning", hvilket giver:

   

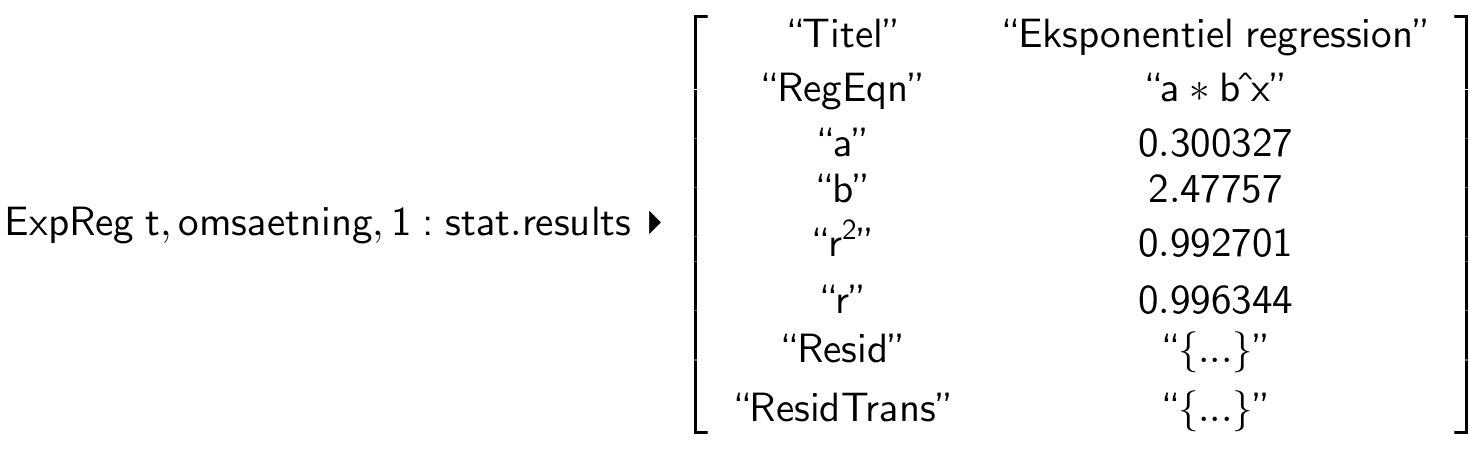
   Af regressionen fremgår det, at a = 2,478 og b = 0,3

   Bemærk: brugen af a og b i Ti-Nspire er den omvendte af den i opgaven.

2. Omsætningen i 2015 er lig med f(4) = 11,32 mia. kr. (beregnet i Geogebra)

   Den årlige vækstrate er (2,478 - 1)·100% = 148 %.

3. Fordoblingstiden er ln(2)/ln(a) = ln(2)/ln(2,478) = 0,764 år = 9 måneder

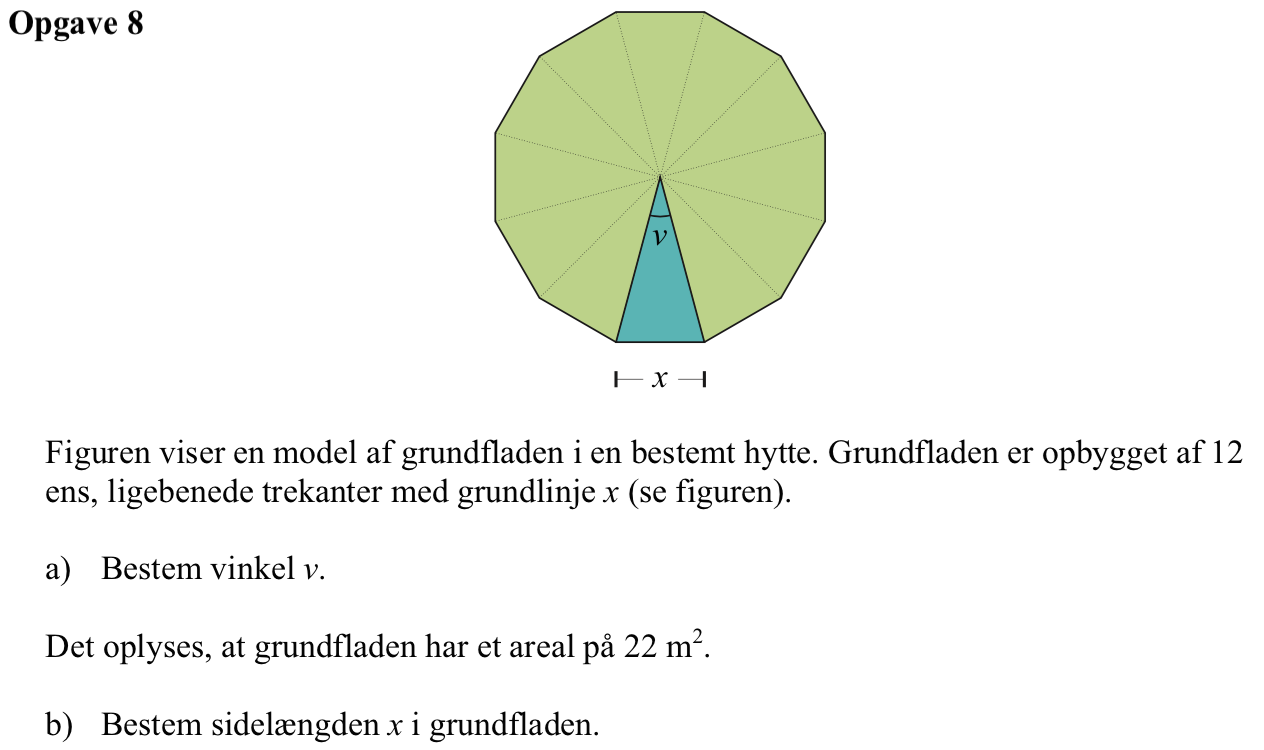
Svar på opgave 8:

1. Vinklen v = 2π/12 = π/6 = 0.5236^rad eller 30°.

2. Arealet af en regulær 12-kant med siden x er

   

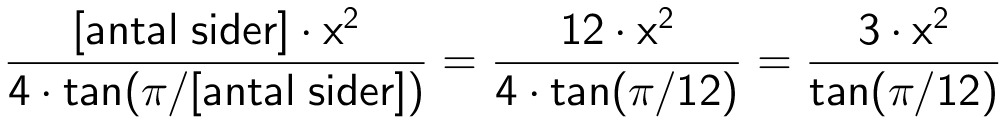
   Idet værdien af arealet er 22, finder man x i Ti-Nspire med kommandoen:

   solve(3*x²/tan(π/12)=22.0,x)|x>0 ▸ x=1.40177

   Dvs. længden af siden i grundfladen er 1,402

   Bemærk: hvis man vil bruge 15° i stedet for 12/π, skal man huske gradtegnet, ellers vil Ti-Nspire opfatte det som 15 radianer.

Svar på opgave 9:

1. For at finde nulpunkterne definerer man først f(x) i Ti-Nspire: f(x):=x³-5*x²+4*x ▸ Udført.

   Derefter finder man nulpunkterne for f(x) med kommandoen:

   solve(f(x)=0,x) ▸ x=0 or x=1 or x=4

   Dvs. nulpunkterne er x = 0, x = 1 eller x = 4

2. Man skal bestemme fortegns-intervaller for f´(x). Man får i Ti-Nspire:

   

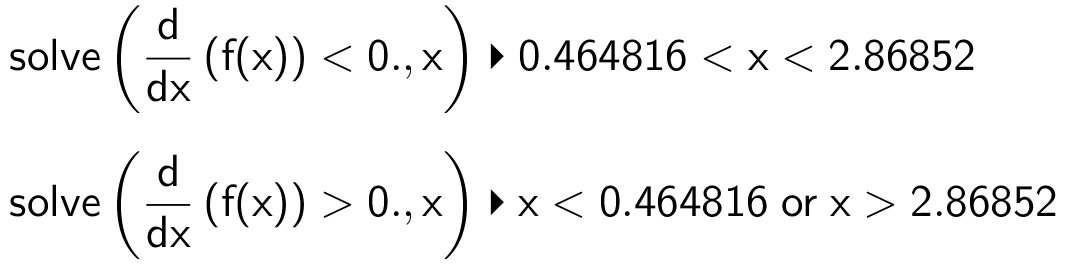
   Af dette fremgår det, at f(x) er voksende for x < 0,4648, aftagende for 0,4648 < x < 2,869 og voksende for x > 2,869

3. Idet tangentens hældning er 1 (y = 1·x - 9), skal man finde x, så f´(x) = 1. Det gøres i Ti-Nspire med kommandoen :

   solve(g(x)=1.,x) ▸ x=0.3333 or x=3.

   Dvs. første koordinaten til Q er 0,333, idet x = 3 er førstekoordinaten til P.

Svar på opgave 10:

1. Der er tale om en uafhængighedstest. Man opretter en matrix med de observerede værdier:

   

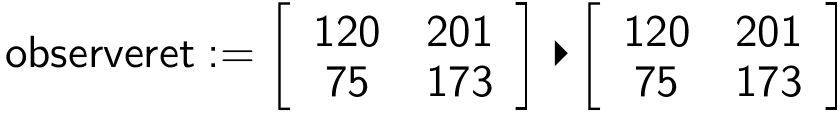
   Man vælger kommandoen: Statistik > Statistiske test > Χ²-uafhængighedstest... , vælger "observeret" på listen over matricer og får:

   

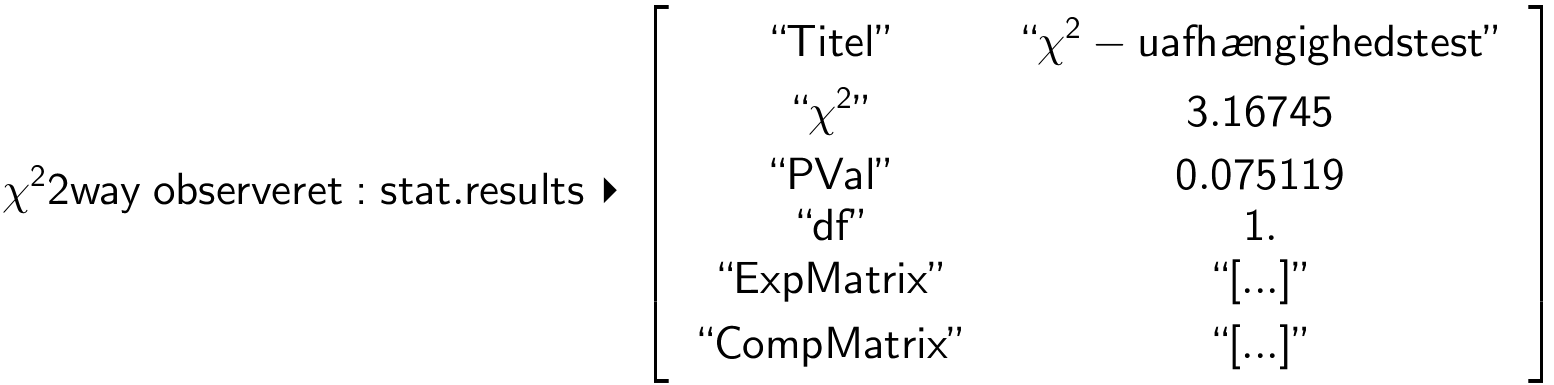
   Herefter skaber man en matrix med de forventede værdier:

   

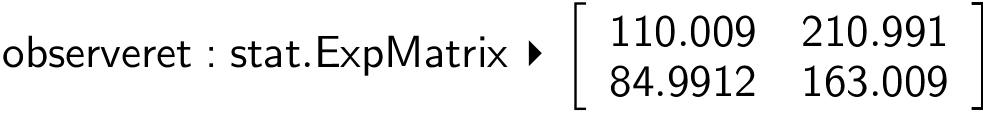
   PVal er sandsynligheden for at testørrelsens værdi kan forklares ved tilfældighed. Da PVal = 0,075 = 7,5% og dermed større end 5% accepteres nulhypotesen.

2. Man får følgende matrix af nye observerede værdier efter, at tallene for "bor sammen med en forældre" er splittet op.

   

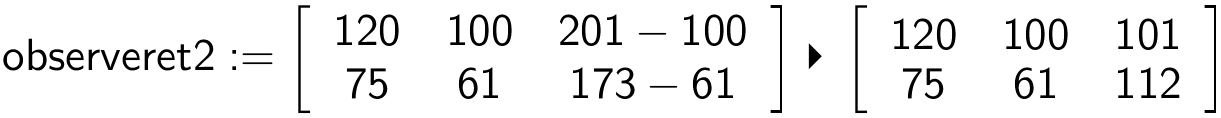
   Man vælger igen kommandoen: Statistik > Statistiske test > Χ²-uafhængighedstest... , vælger denne gang "observeret2" på listen over matricer og får:

   

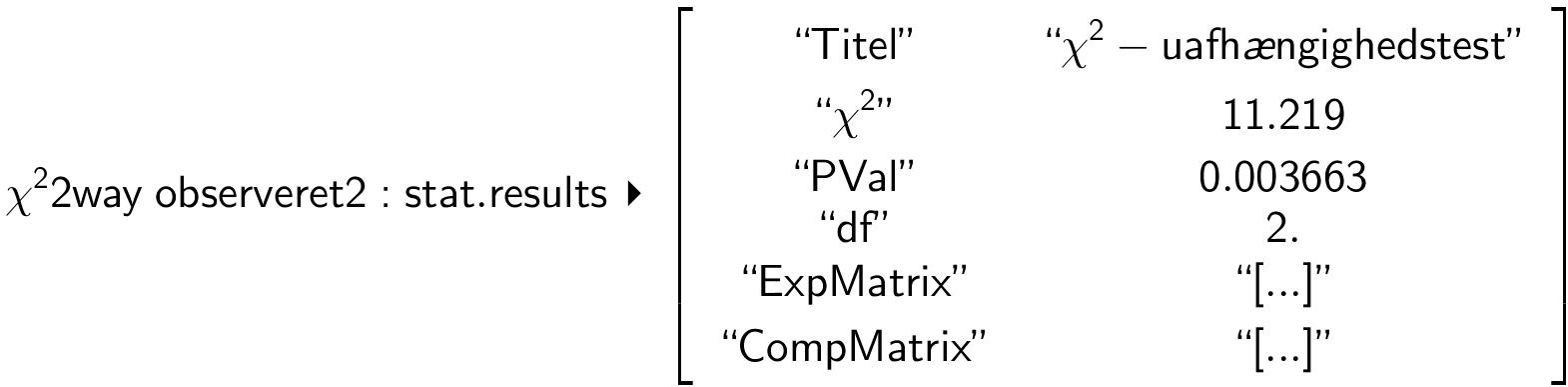
   Her er PVal = 0,0037 = 0,37%, som er mindre end 5% og derfor forkastes nulhypotesen

Svar på opgave 11:

Løsning i Geogebra.

Til venstre på figuren er punkterne og de beregnede værdier, til højre 3D tegningen. Man indsætter punkterne A-E via Geogebras input-felt.

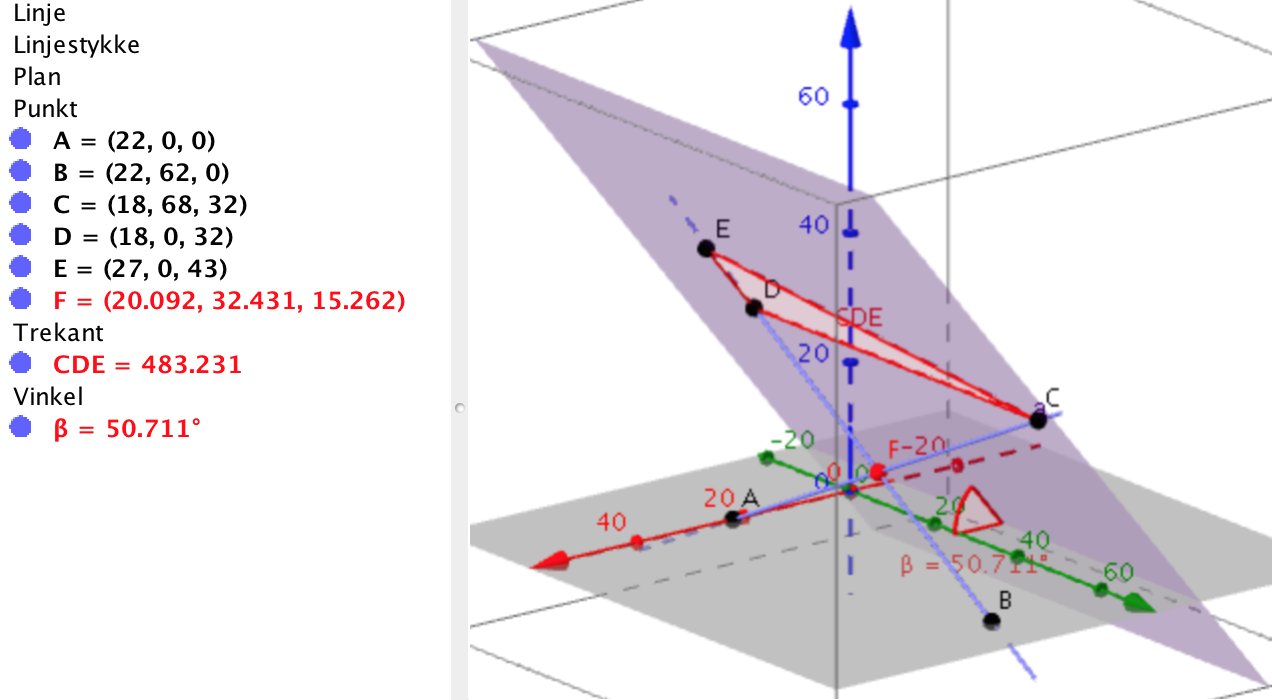
1. Man aktiverer polygon-værktøjet og klikker på C, D, E og C. Dermed får man trekanten som er vist med rødt midt i billedet. Til venstre aflæser man arealet 483,2

2. Man opretter det lilla plan, som C, D og E ligger i, ved at aktivere plan-gennem-tre-punkter værktøjet og klikke på C, D og E. Dernæst vælger man vinkelmåler-værktøjet og klikker på denne plan og dernæst xy-planen. Man får vinklen β = 50,7°

3. Ved hjælp af linje-værktøjet opretter man først en ret linje gennem A og C ved at klikke på de to punkter og dernæst en linje gennem B og D ved at klikke på disse punkter. Ved hjælp af skærings-værktøjet finder man de to linjers skæring ved at klikke på dem.

   Skæringspunktet kaldet F har koordinaterne (20,1;32,4;15,3), som aflæses til venstre.

Løsning i Ti-Nspire. Man starter med at definere punkterne som vektorer:

1. Man finder krydsproduktet af vektor CD og vektor ED. Dernæst finder man arealet som en halv gange længden af krydsproduktet:

   

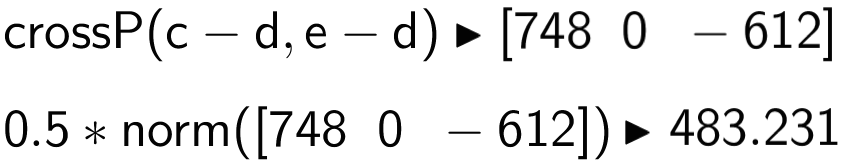
   Arealet er 483

2. Man bruger formlen for cosinus til vinklen mellem normalvektorerne for de to planer for at finde vinklen mellem planerne. Til normalvektor for xy-planen vælges (0,0,1), der er basis-vektor for z-aksen:

   

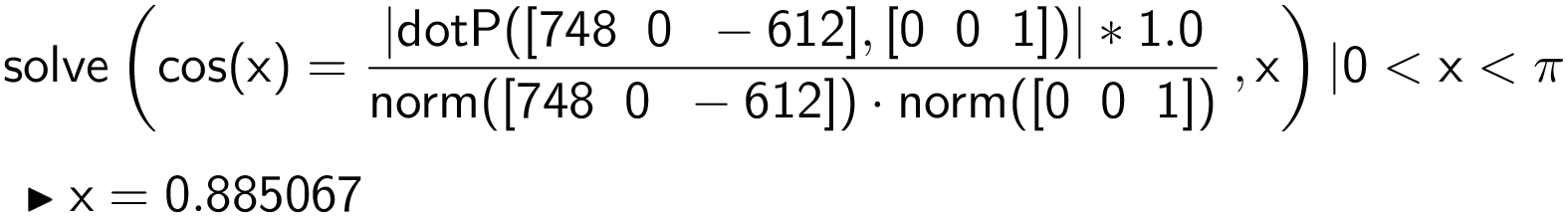
   Efter at have omregnet fra radianer til grader får man vinklen β = 50,7° som vist

   

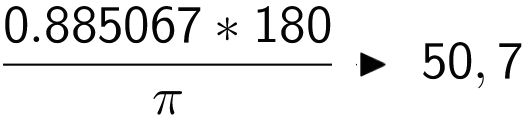
3. Ud fra punkterne A og C opretter man linjen l(t) defineret ved dens parameterfremstilling, idet den går gennem A og har retningsvektoren AC. Det samme gøres med m(s), der er en parameterfremstilling for linjen gennem B og D.

   

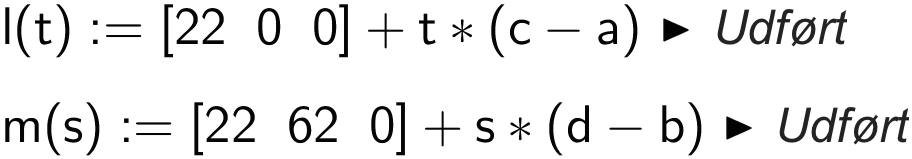
   Man bruger solve() for at finde t værdien for linjernes skæringspunkt.

   

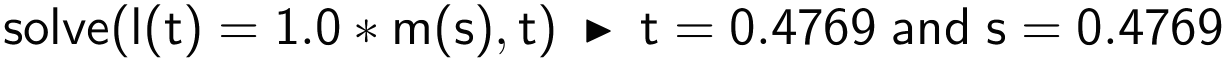
   Den fundne t-værdi indsættes i l(t).

   

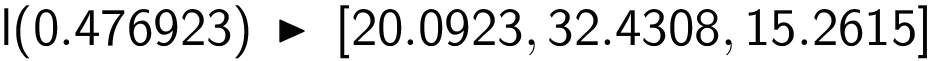
   Skæringspunktet har koordinaterne (20,1; 32,4; 15,3)

Svar på opgave 12:

1. Hastigheden er lig med y'(t) når y(t) = 1,2 mg/L og findes af differentialligningen til -0,03·1,2 mg/L/time = -0,036 mg/L/time

2. Løsning i Geogebra:

   Differentialligningen løses i Geogebras CAS modul. Her bruges x i stedet for t.

   

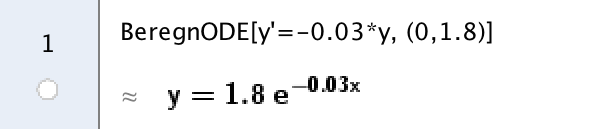
   Løsningen er med t indsat: y(t) = 1,8·e^-0,03·t

   For at kunne beregne koncentrationen af klor til tiden 24 timer indfører man f(x) og sætter den lig med udtrykket for y (stadig med x i stedet for t).

   

   Man skal beregne f(24) og får

   

   Dvs. koncentrationen af klor er 0,876 mg/L efter 24 timer.

   Løsning i Ti-Nspire:

   Man bruger desolve-kommandoen:

   deSolve(y'=−0.03*y and y(0)=1.8,t,y) ▸ y=1.8*(0.970446)^t

   Dvs. y(t) = 1,8·(0,9704)^t

   Man finder værdien af y(24):

   1.8*(0.9704)²⁴ ▸ 0.876

   Dvs. koncentrationen efter 24 timer er 0,876 mg/L

Svar på opgave 13:

1. Grafen for f tegnes i Geogebra med t ud af første-aksen:

   

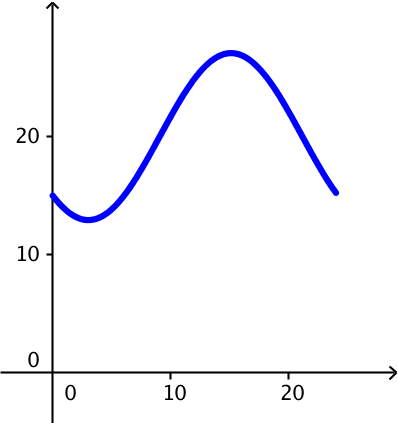
   Man finder minimum og maksimum i Geogebra med funktionsundersøgelses-værktøjet:

   

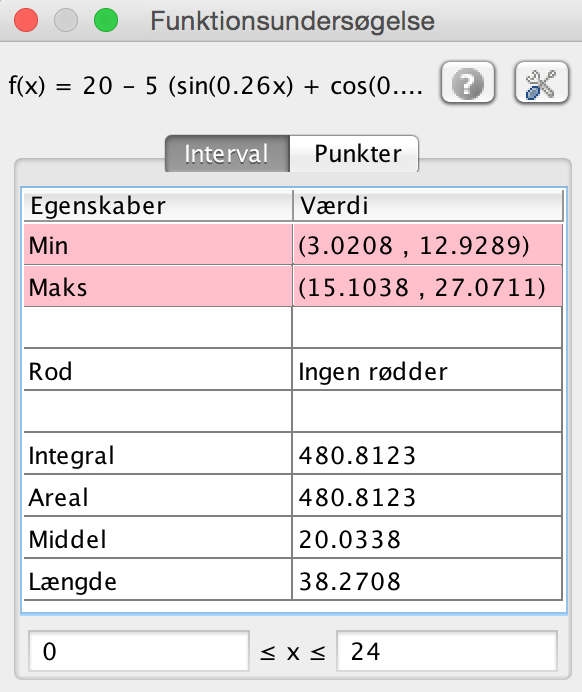
   Minimum aflæses til 12,9 °C og maksimum til 27,1 °C

   Løst i Ti-Nspire:

   f(t) defineres:

   f(t):=20-5*(sin(0.262*t)+cos(0.262*t))|0≤t≤24 ▸ Udført

   Den t-værdi, der giver minimumsværdien af f(t) findes med fMin()-kommandoen:

   fMin(f(t),t) ▸ t=2.9977

   Ved indsættes af dette i f(t) får man minimum for funktionen:

   f(2.9977) ▸ 12.93

   Tilsvarende finder man maksimum-værdien for f(t):

   fMax(f(t),t) ▸ t=14.9885

   f(14.9885) ▸ 27.07

   Dvs. mindste temperatur er 12,9 °C og højeste temperatur er 27,1 °C

2. Man finder f´(8) i geogebra:

   

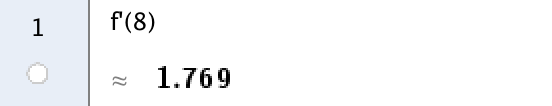
   Dette tal er antallet af grader celsius, som temperaturen ændrer sig med i timen kl. 8 om morgenen, dvs. 1,8°C

Svar på opgave 14:

1. Grafen for f er en halvcirkel, som er tegnet i Geogebra og vist med grønt:

   

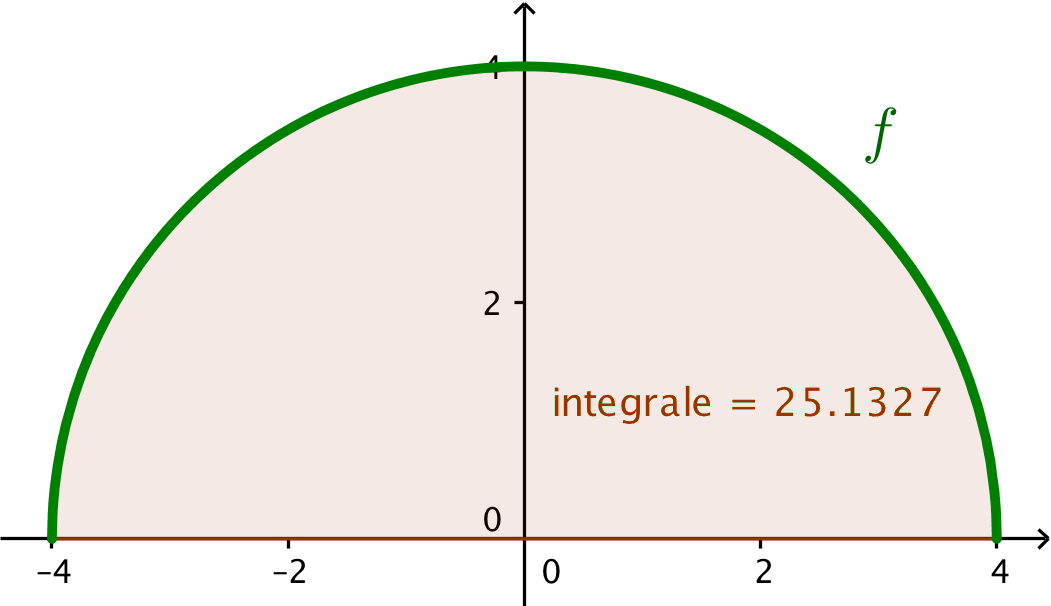
   f(x) oprettes i Geogebra ved at skrive sqrt(4^2-x^2) i input-feltet og trykke enter. Integralet fra x = -4 til x = 4 beregnes med Geogebra-kommandoen: Integral[f,-4,4] ▸ 25,133

   Resultatet og punktmægden under kurven er vist med brunt på ovenstående billede.

2. Man skal bestemme radíus, kaldet a, i en halvcirkel, hvis areal er 4. Man får: 0,5·a²·π = 4 ⇒ a = √[8/π] = 1,60