Svar på opgave 1:

1. Ligningen er en andengradsligning skrevet på standardform: ax² + bx + c = 0, hvor a = 1, b = 2 og c = -35. Løsningen er:

   

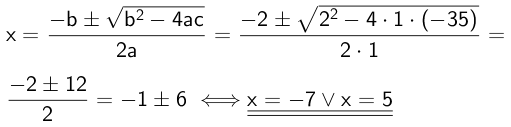
Svar på opgave 2:

1. Modellen er: f(x) = 25x + 420, hvor x er antal år efter 2010 og f(x) er antallet af medlemmer. Modellen er linært voksende med en årlig tilvækst på 25 medlemmer. Antal medlemmer ved start er 420.

Svar på opgave 3:

1. Man differentierer f(x) med produktreglen:

   

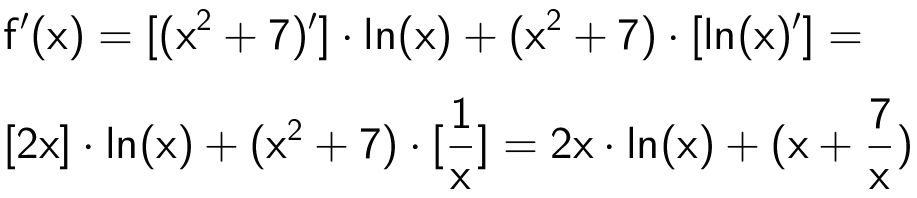
   Man finder f'(1) ved at indsætte x = 1:

   

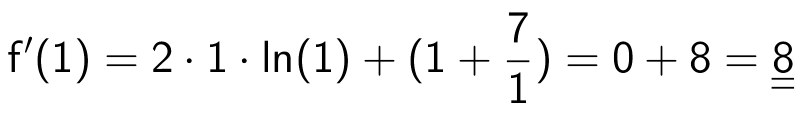
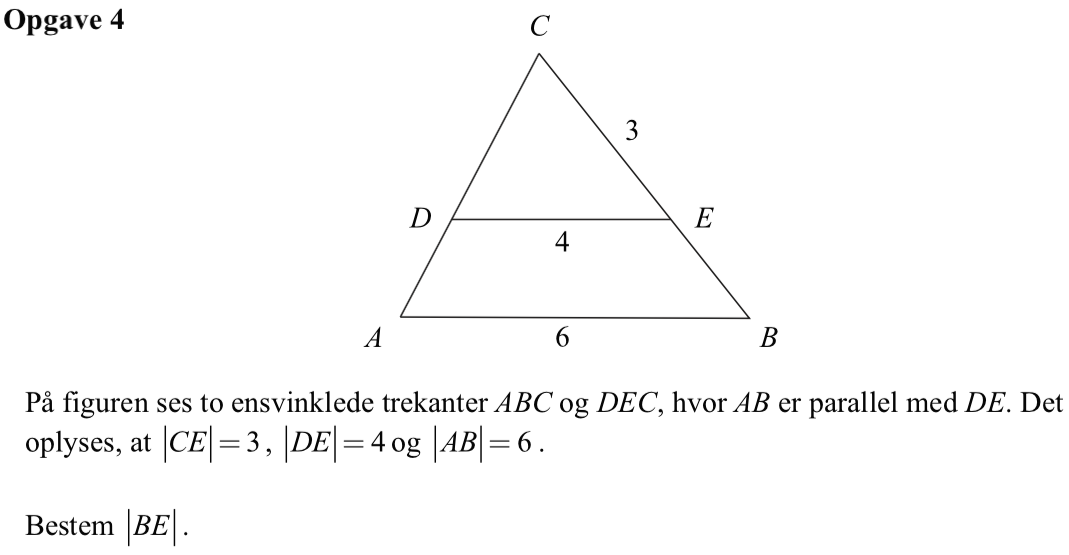
Svar på opgave 4:

1. Skaleringsfaktoren er |AB|/|DE| = 6/4 = 1,5. |CE| + |EB| = 1,5·|CE| ⇒ 3 + |BE| = 1,5·3 ⇒ |BE| = 1,5

Svar på opgave 5:

1. En vilkårlig stamfunktion til f(x) kaldet F(x) kan findes som det ubestemte integrale af f(x).

   

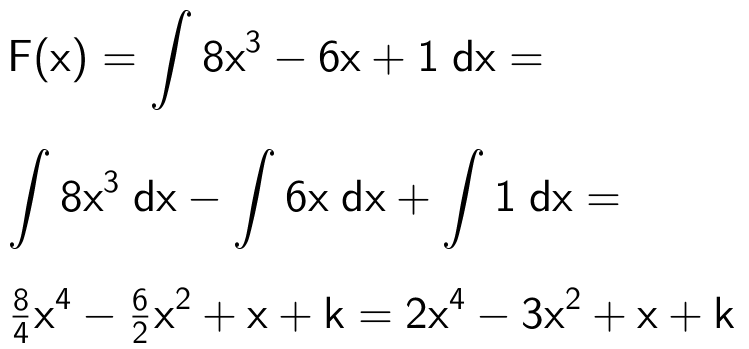
   Man skal finde den stamfunktion, hvorom det gælder, at F(2) = -6. Dette giver følgende ligningen i k: 2·2⁴ - 3·2² + 2 + k = -6 ⇔ 22 + k = -6 ⇔ k = -28.

   Man får dermed, at den søgte stamfunktion er: 2x⁴ - 3x² + x - 28

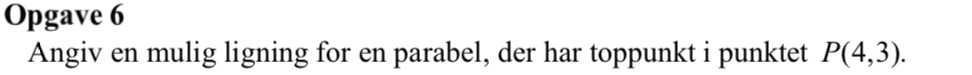
Svar på opgave 6:

1. Parablen y = x² har toppunkt i (0,0). En parabel med toppunkt i (4,3) kan laves ved at parallelforskyde denne parabel med vektoren (4,3).

   Dette giver: (y - 3) = (x - 4)² ⇔ y = x² - 8x + 19

Svar på opgave 7:

1. Man skal undersøge om skalarproduktet af a og b er nul. Man får: a · b = (1,3)·(2,-2) = 1·2 + 3·(-2) = -4 ≠ 0. Dermed er a og b ikke ortogonale.

2. Da a er parallel med l gælder, at tværvektoren til a er en normalvektor til l. Tværvektoren til a er (-3,1). Når man kender en normalvektor (-3,1) til linjen og punktet (-8,1) på linjen er dens ligning:

   l: -3·(x - (-8)) + 1·(y - 1) = 0 ⇔ -3·(x + 8) + (y - 1) = 0 ⇔ -3x + y - 25 = 0

Svar på opgave 8:

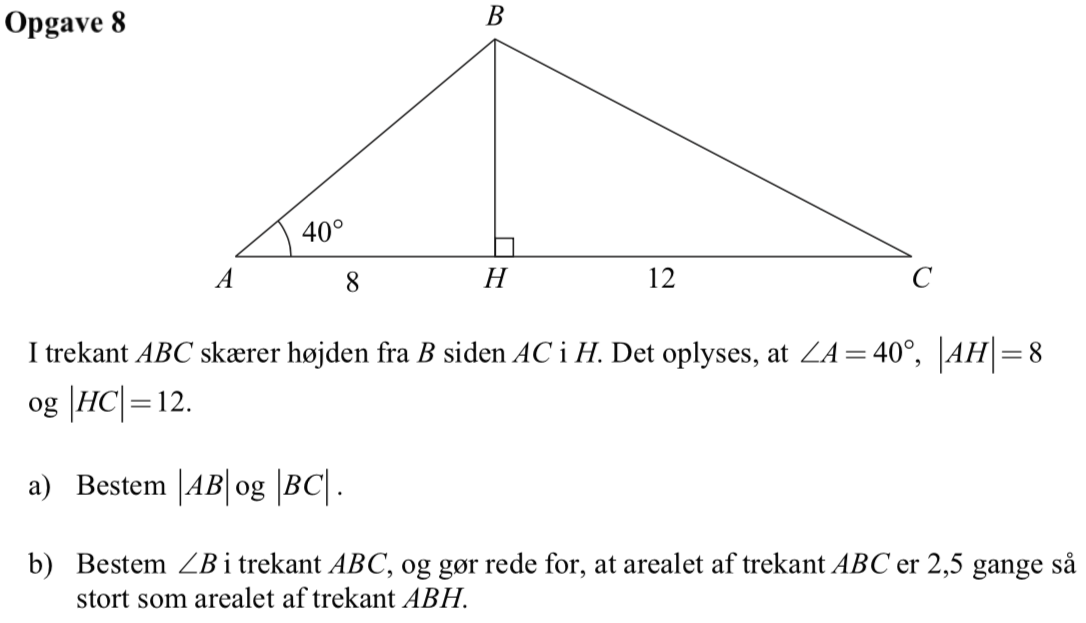
1. Trekant ABH er retvinklet med AB som hypotenusen og AH dens hosliggende katete i forhold til vinklen A. Der gælder, at |AB|·cos(∠A) = |AH| ⇒ |AB| = 8/cos(40°) = 10,44

   |BC| kan findes ved hjælp af Pythagoras læresætning, idet |BC|² = |BH|² + 12².

   |BH|² findes ved at anvende Pythagoras læresætning på trekant ABH, hvilket giver: |BH|² = 10,44² - 8² = 45,06.

   Dette indsættes i den første ligning: |BC|² = 45,06 + 144 = 189,06. Tager man kvadratroden af dette, får man: |BC| = 13,75

2. ∠B kan findes ved hjælp af cosinusrelationen.

   Der gælder, at cos(∠B) = (|AB|² + |BC|² - |AC|²)/(2·|AB|·|BC|) ⇒ cos(∠B) = (10,44² + 13,75² - 20²)/(2·10,44·13,75) ⇒ cos(∠B) = -0,3551 ⇒ ∠B = cos^-1(-0,3551) ⇒ ∠B = 110,8°

   Arealet af trekant ABC er 0,5·|BH|·|AC| = 0,5·|BH|·(8 + 12) = 10·|BH|. Arealet af trekant ABH er 0,5·|BH|·8 = 4·|BH|.

   Forholdet mellem deres arealer er derfor: (10·|BH|)/(4·|BH|) = 10/4 = 2,5

Svar på opgave 9:

Lavet i Ti-Nspire

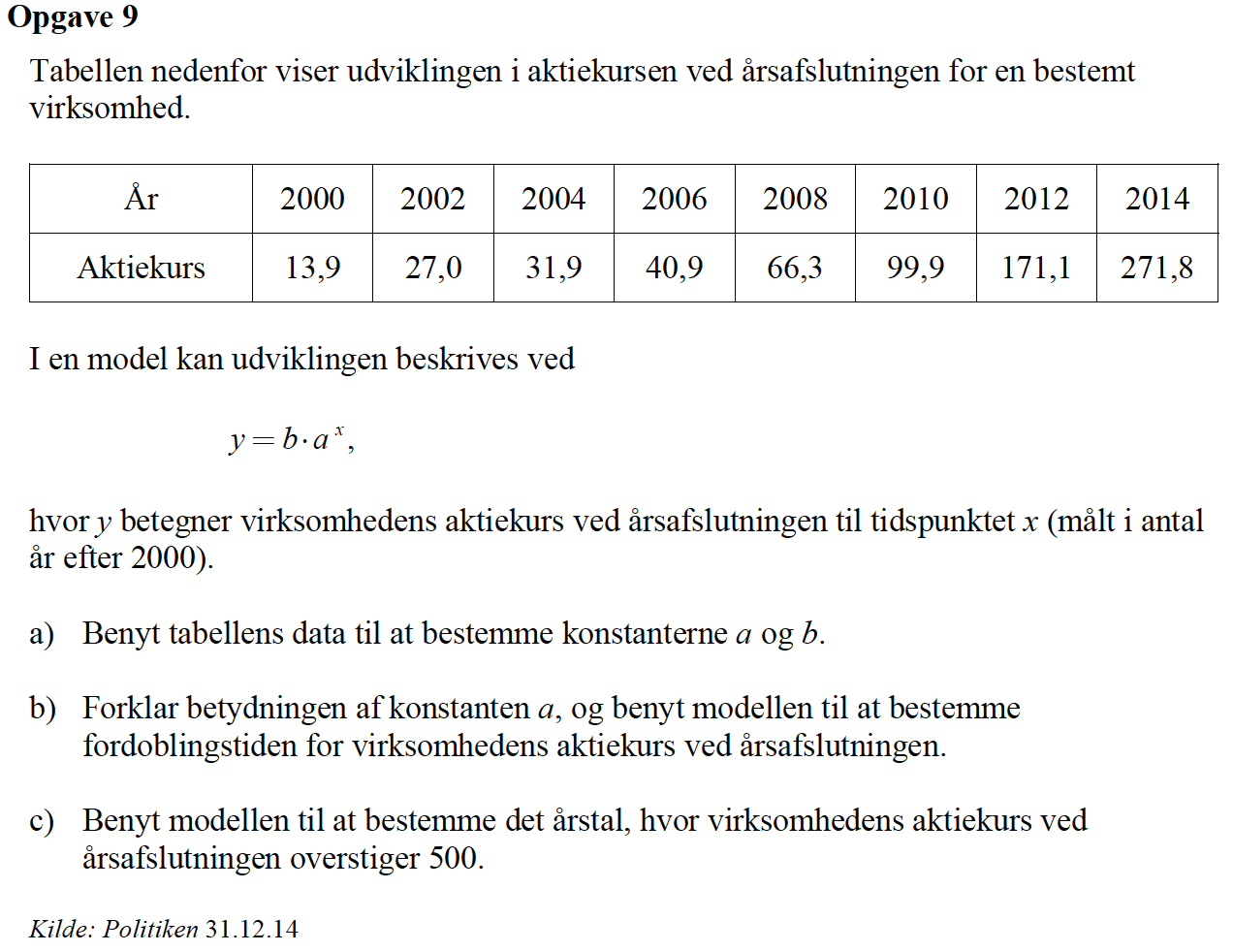
1. Man opretter lister for x og aktiekurs, hvor x er antallet af år efter 2000.

   x:={0,2,4,6,8,10,12,14} ▸ {0,2,4,6,8,10,12,14} og

   aktiekurs:={13.9,27,31.9,40.9,66.3,99.9,171.1,271.8} ▸ {13.9,27,31.9,40.9,66.3,99.9,171.1,271.8}

   Man bruger kommandoen: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression og vælger de to lister. Man får resultatet:

   

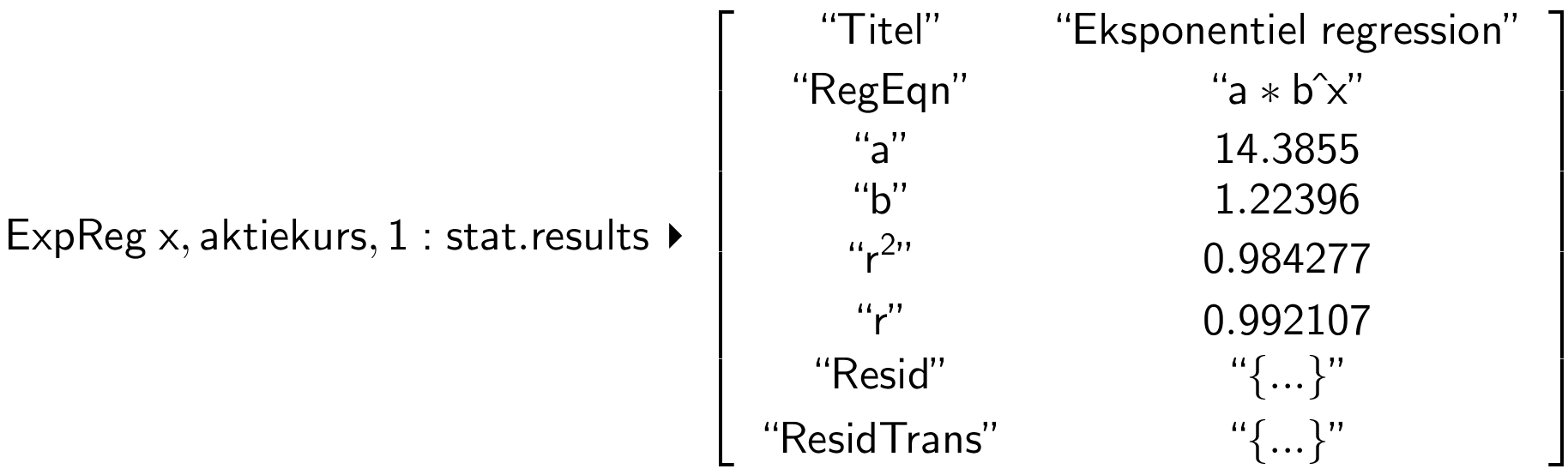
   Af figuren ses (idet a og b skal byttes om) at: a = 1,224 og b = 14,386.

2. Konstanten a er fremskrivningfaktoren. Det er det tal, som den gamle kurs hvert år ganges med, for at få den nye. (Vækstraten er a - 1).

   Fordoblingstiden, T, for en eksponentiel voksende funktion, hvor tiden måles i år, er T = ln(2)/ln(a) år = 0,693/0,202 år = 3,45 år

3. Man skal findes det x, hvorom det gælder, at y(x) = 500. Beregningen af x er vist nedenunder:

   solve(14.386*1.224^x=500,x) ▸ x=17.5553

   Dette lægges til 2000 og man får, at kurs 500 passeres 17,6 år efter afslutningen af år 2000, dvs. årstallet er 2018

Svar på opgave 10:

1. Funktionen sin(x) har mindsteværdien -1 og størsteværdien +1 (det gælder også her, hvor x blot er udskiftet med 0,52·t - 3,14).

   Dette giver mindste-værdien for d(t): 2·(-1) + 7 m = 5 m og største-værdien: 2·(+1) + 7 m = 9 m

Svar på opgave 11:

1. Figuren nedenunder viser grafen for f med grønt og integralerne af de to områder. Tegnet i Geogebra.

   

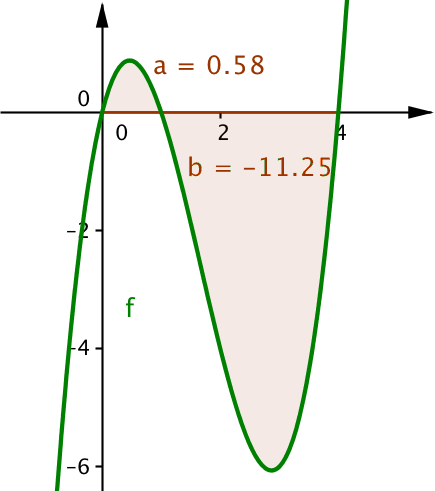
   Det samlede areal er 0,58 + 11,25 = 11,83

2. For at beregne rumfanget skal man kende grænserne for de to områder. Grænserne findes i ti-Nspire til x = 0, x = 1 og x = 4 som vist:

   solve(x^3-5*x^2+4*x=0,x) ▸ x=0 or x=1 or x=4

   Dernæst skal man bruge formlen for rumfang af et omdrejningslegeme ved rotation om x-aksen:

   

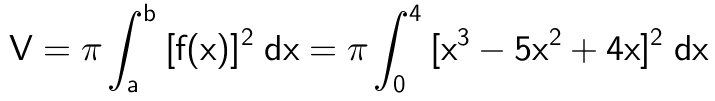
   Den beregnes i Ti-Nspire til: 168,51

Svar på opgave 12:

1. A'(t) = [8·t^1,5]' = 8·1,5·t^0,5 = 12·t^0,5. Heraf får man: A'(100) = 12·100^0,5 m²/time = 120 m²/time. Dette tal er den væksthastighed, som oliepletten har efter 100 timer.

2. Det maksimale areal (i m²) findes ved at indsætte 1,5 m³ (uden enhed) i formlen for A_max.

   Det giver maksimum-arealet: A_max = 10⁴·1,5^0,75 m² = 13.554 m²

   For at finde tidspunktet, hvor olieudslippet har nået sit maksimale areal, skal man løse ligningen: A(t) = A_max = 13.554 m² med hensyn til t. Dette giver i Ti-Nspire:

   solve(8*t^1.5=13554,t) ▸ t=142.119

   Det tager med andre ord 142 timer før olieudslippet når sin maksimale størrelse.

Svar på opgave 13:

1. Ligningen for en kugle med centrum i punktet (a,b,c) og radius r kan skrives: (x - a)² + (y - b)² + (z - c)² = r². I dette tilfælde er a = 2, b = 3, c = -4 og r = 5.

   Dette giver ligningen for kuglen: (x - 2)² + (y - 3)² + (z + 4)² = 5²

   Punktet P ligger på cirklen, idet det opfylder cirklens ligning: (6 - 2)² + (0 - 3)² + (-4 + 4)² = 4² + 3² + 0² = 25 ✔

2. Ligningen til en plan, der har normalvektoren (a, b, c) og indeholder punktet (x₀, y₀, z₀) har ligningen: a·(x - x₀) + b·(y - y₀) + c·(z - z₀) = 0. P ligger i planen α, og vektoren PC er en normalvektor til planen, da tangentplanen til en kugle står vinkelret på radius. PC = (6, 0, -4) - (2, 3, -4) = (4, -3, 0).

   Dette indsættes og man får ligningen for planen α: 4·(x - 6) + (-3)·(y - 0) + 0·(z - (-4)) = 0 ⇒ 4x - 3y - 24 = 0

3. Linjen m ligger i planen α, hvis dens retningsavektor (0,0,-6) er vinkelret på planens normalvektor (4, -3, 0), dvs. hvis de to vektorers skalarprodukt er 0. Man får skalarproduktet: (0, 0, -6)·(4, -3, 0) = 0·4 + 0·(-3) + (-6)·0 = 0. Dermed ligger m i α.

   Linjen m skærer eller rører kuglen, hvis den indeholder punktet P, der er det eneste punkt i planen, der ligger på kuglefladen. Dette kræver at P's koordianter opfylder linjens ligning. Det ses at ikke være tilfældet, da alle punkter på m har x-koordianten = 3 og y-koordinaten = -4, hvilket P ikke har. Dermed skærer linjen m ikke kuglen.

Svar på opgave 14:

Beregninger i Geogebra.

1. h isoleres fra volumenformlen idet V sættes lig med 1000. Af Ti-Nspire beregningerne nedenunder følger, at h = 5000·0,0769 / a² = 384,5/a²

   v(h):=2.6*a^2*h ▸ Udført

   solve(v(h)=1000,h) ▸ h=384.615/(a^2)

2. Man definerer O(h) og bruger fMin() kommandoen i Ti-Nspire, idet man forudsætter, at h = 384.615/a^2 og a>0. Det giver:

   o(h):=2.6*a^2+6*a*h ▸ Udført

   fMin(o(h),a)|h=(384.615/a^2) and a>0 ▸ a=7.62766

   Man får resultatet a = 7.628.

Svar på opgave 15:

1. p = 3 og s = 7000 indsættes i differentialligningen, hvor startbetingelsen A(0) = 50.000 kr. er medtaget. Man får i Ti-Nspire

   deSolve(a'=3*a/100+7000 and a(0)=50000.,t,a) ▸ a=283333.*1.03045^t-233333.

   A(t) = 28,3333·1,03^t - 23,3333 kr.

   Der går 5,4 år før beløbet når op på 100.000 kr. Det er fundet i Ti-Nspire:

   solve(283333.*1.03045^t-233333.=100000,t) ▸ t=5.4181

2. p = 2,5 og begyndelsesbetingelsen A(0) = 30.000 kr. indsættes i differentialligningen og den løses i Ti-Nspire.

   deSolve(a'=(2.5*a/100)+s and a(0)=30000,t,a) ▸ a=s*(40.*1.02532^t-40.)+30000.*1.02532^t

   Man skal nu løse ligningen A(8) = 70.000 med hensyn til s ved hjælp af nedenstående beregning:

   solve(s*(40.*1.02532^t-40.)+30000.*1.02532^t=70000,s)|t=8 ▸ s=3765.71

   Årligt indsat beløb = 3765,71 kr.