Svar på opgave 1:

1. Når x = 7, bliver y = 3·7 + 4 = 25. Væksten bliver: 3·5 = 15

Svar på opgave 2:

1. Der er tale om eksponentiel vækst, fordi prisen vokser med en konstant procent­sats hvert år.

   De variable er: x, antal år efter 2015 og y, prisen i kr.

   Til en eksponentiel vækstmodel hører en startværdi (prisen for x = 0) og en fremskrivningsfaktor. Startværdien er 213 kr. og fremskrivnings­faktoren er 1 + 4,5% = 1,045. Modellen bliver:

   f(x) = 213·1,045^x, x > 0

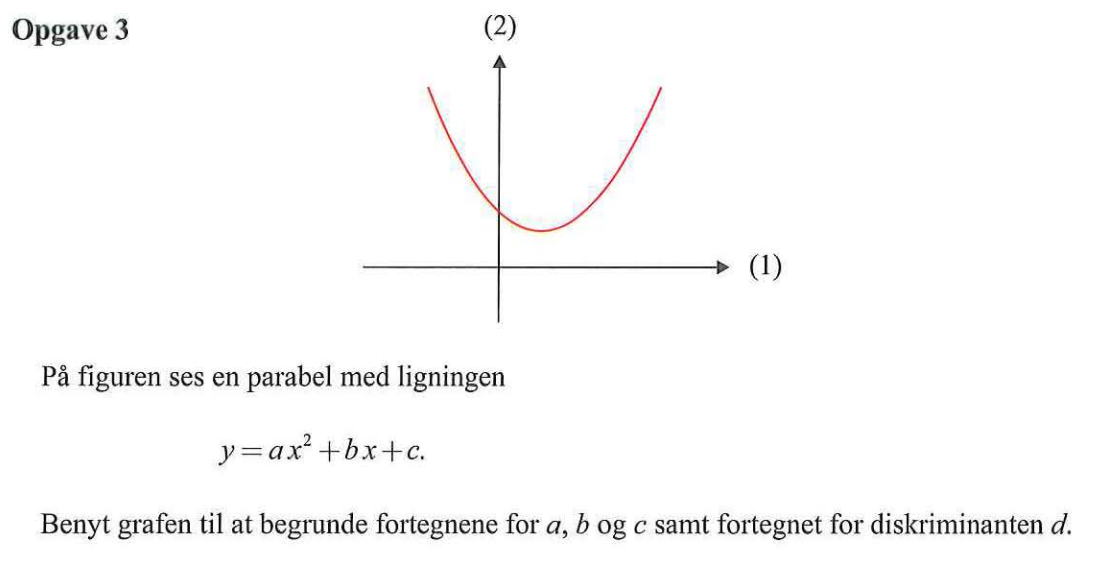
Svar på opgave 3:

1. a > 0, da grenene på kurven vender opad.

   b < 0, da hødningen til kurven er negativ, der hvor den skærer y-aksen.

   c > 0, da kurven skærer y-aksen i en værdi, der er større end 0.

   d < 0, da kurven ikke skærer x-aksen.

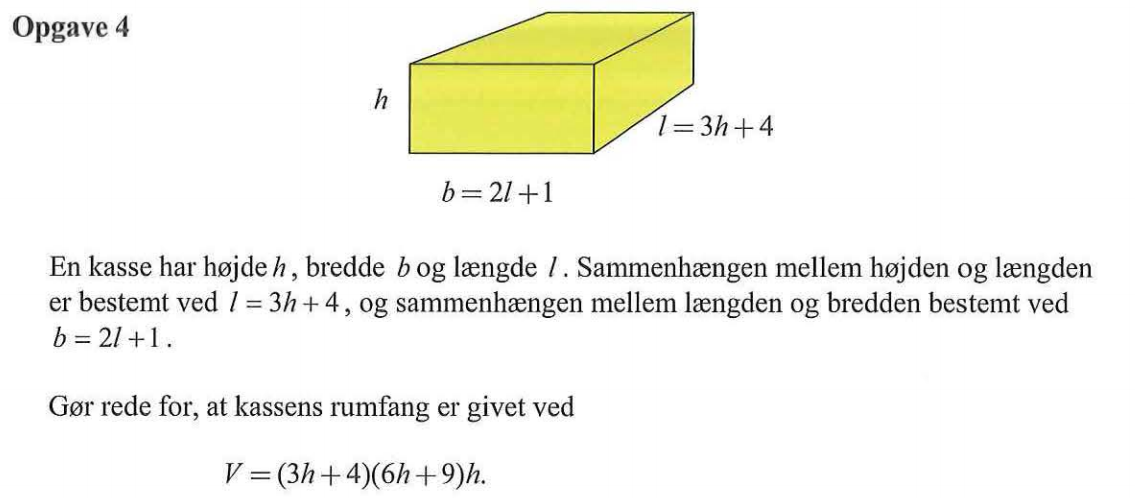
Svar på opgave 4:

1. V = l·b·h = (3h + 4)·(2l + 1)·h = (3h + 4)·(2(3h + 4) + 1)·h = (3h + 4)·(6h + 9)·h

Svar på opgave 5:

1. Man indsætter f(x) = x·e^x på begge sider af differentialligningen og ser, om man får det samme.

   Venstre side giver:

   

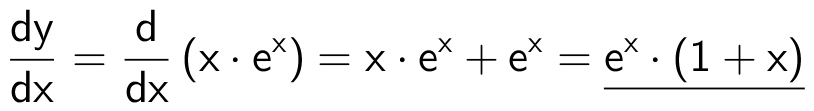
   Højre side giver:

   

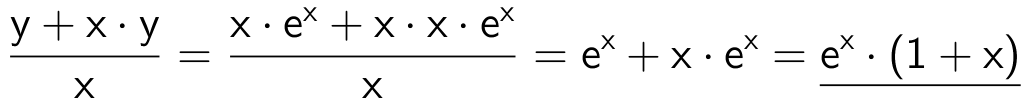
   Da venstre og højre side er ens, er f(x) en løsning.

Svar på opgave 6:

1. Man laver substitutionen:

   

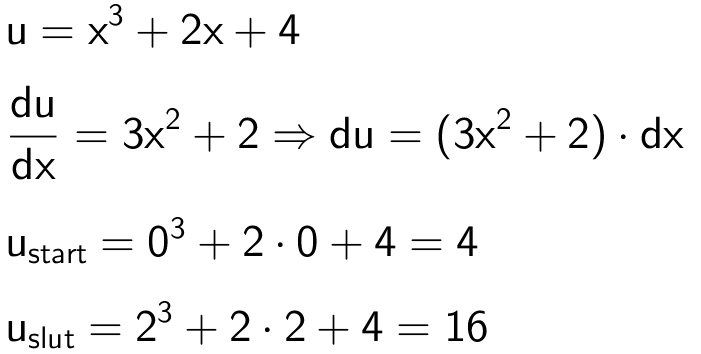
   Dette giver:

   

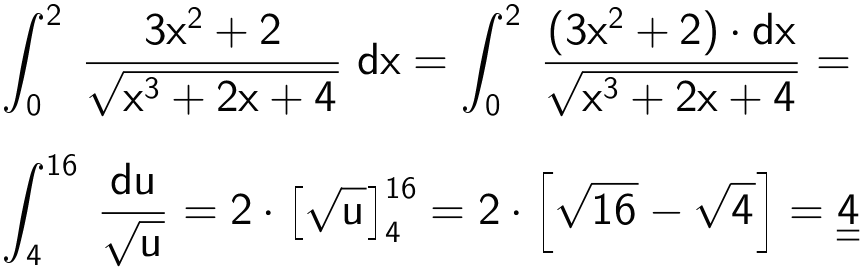
Svar på opgave 7:

1. Man skal finde de t, for hvilke skalarproduktet af de to vektorer er 0:

   

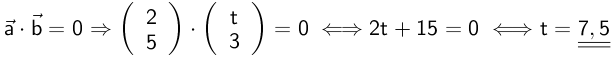
2. Man skal løse følgende ligning med hensyn til t:

   

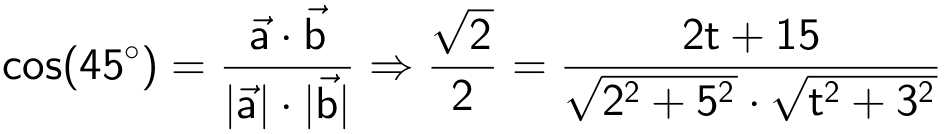
   Den løses i TiNspire:

   

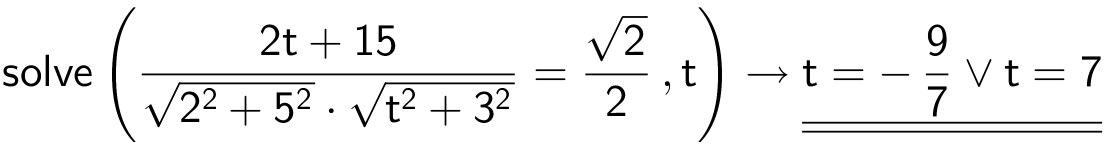
Svar på opgave 8:

Løst i Geogebra.

1. Man sætter tallene ind i et regneark og indfører variablen x = årstal - 2007:

   

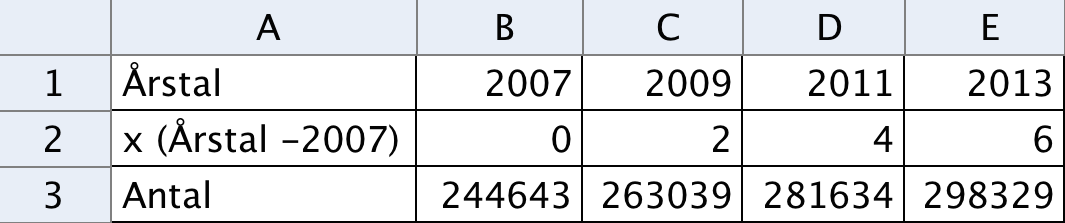
   Heraf får man ved hjælp af tovaribel-regressionsanalyse følgende lineære regressionskurve:

   

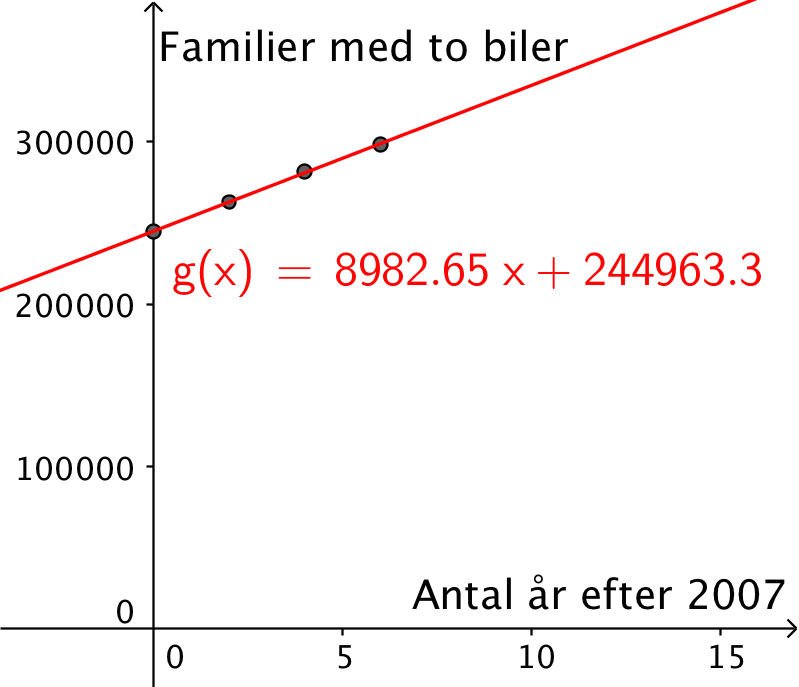
   Det fremgår af figuren, at a = 8.983 og b = 244.963

2. a er væksten målt i antal familier pr. år.

   Antallet af familier med to biler i 2020 er: f(2020-2007) = f(13) = 8.983·13 + 244.963 = 361.738 biler

Svar på opgave 9:

1. Man bruger cosinusrelationen:

   

   

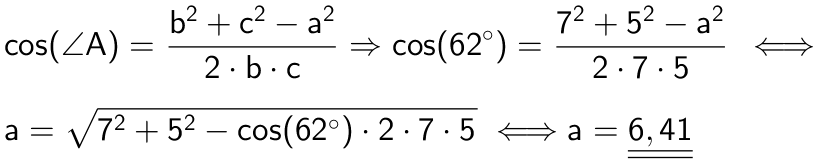
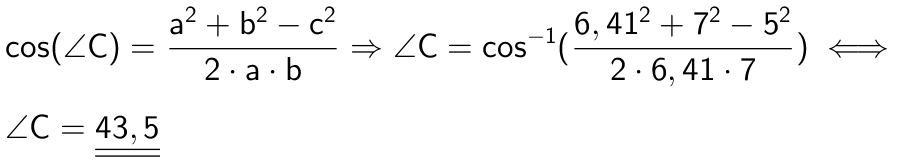
   Det samme løst i Geogebra:

   

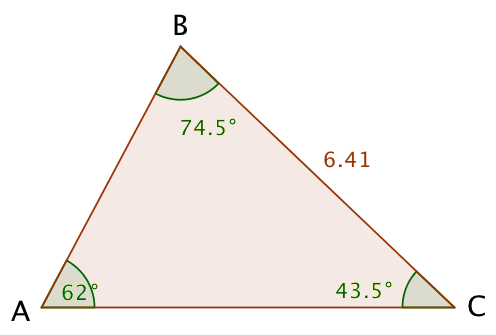
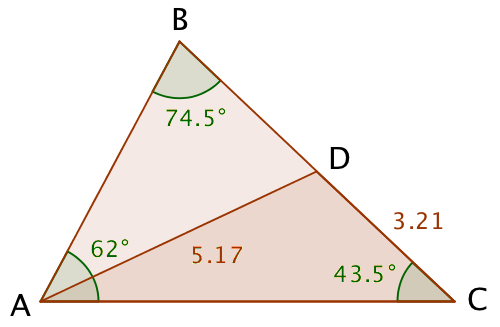
2. En median deler en trekant i to trekanter med samme areal. D er dermed punktet hvor medianen fra hjørnet A skærer siden a. Da |BC| = 6,41 er |CD| = 3,21. Man finder derefter |AD| med cosinusrelationen:

   

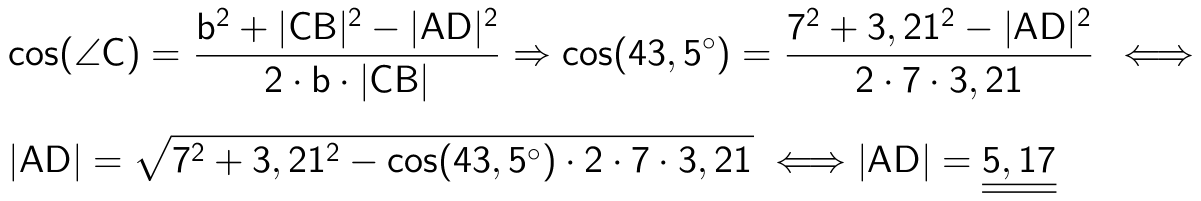
   Det samme løst i Geogebra:

   

Svar på opgave 10:

Løsning i Ti-Nspire.

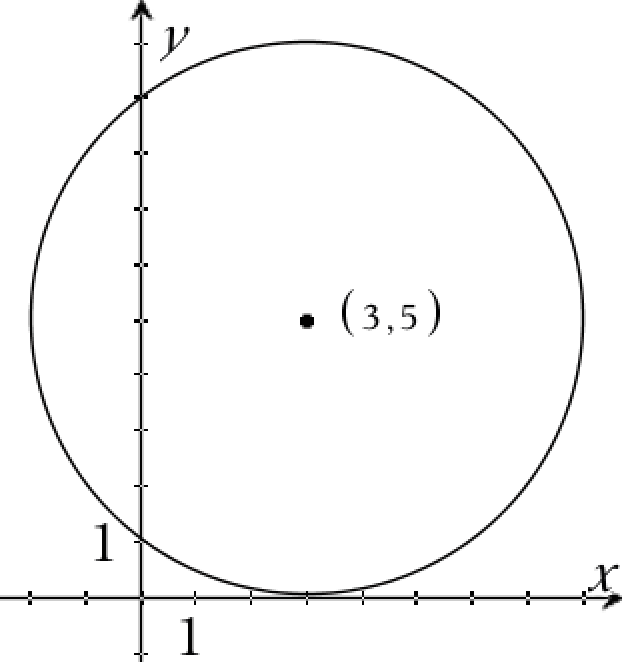
1. Man skal vise, at afstanden fra cirklens centrum til førsteaksen er lig med radius.

   Afstanden fra centrum til førsteaksen er lig med centrums y-værdi = 5, hvilket ses af cirklens ligning. Radius = √25 = 5, hvormed det ønskede er bevist.

   

2. Tangenternes røringspunkter kan findes som skæringspunkterne mellem cirklen og en linje gennem centrum og vinkelret på linjen y = (4/3)·x.

   Denne linje har ligningen - ¾·x + b, hvor b kan findes ved at indsætte centrumskoordinater i ligningen: - ¾·(3) + b = 5 ⇒ b = 29/4. Skæringspunkterne findes ved Ti-Nspire kommandoen:

   solve(y=(−3/4)*x+(29/4) and (x-3)²+(y-5)²=25.,x,y) ▸ x=−1. and y=8. or x=7. and y=2.

   Dette giver skæringspunkterne: (x,y) = (-1,8) og (x,y) = (7,2)

Svar på opgave 11:

1. Geogebra:

   Man får følgende grønne kurve for G(t) (x er valgt i stedet for t, da det er lettere i Geogebra).

   G(2) = 161,8 mg/dl

   

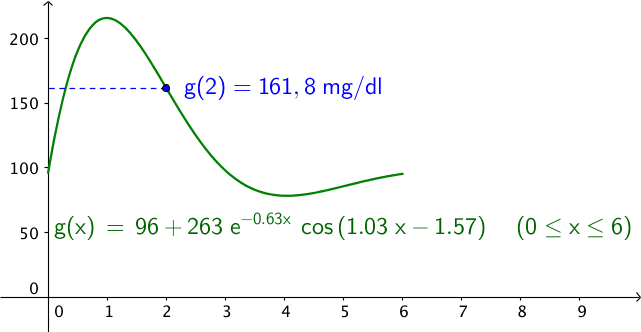
2. Ti-Nspire:

   Man definerer G(t) og løser G'(t) = 0 ved hjælp af kommandoerne:

   

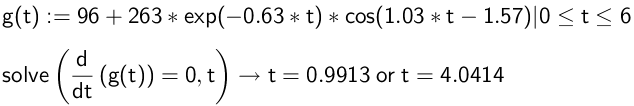
   Man beregner derefter G(0,9913) og G(4,0414) for at finde henholdsvis maksimums- og minimumsværdien (se nedenstående figur).

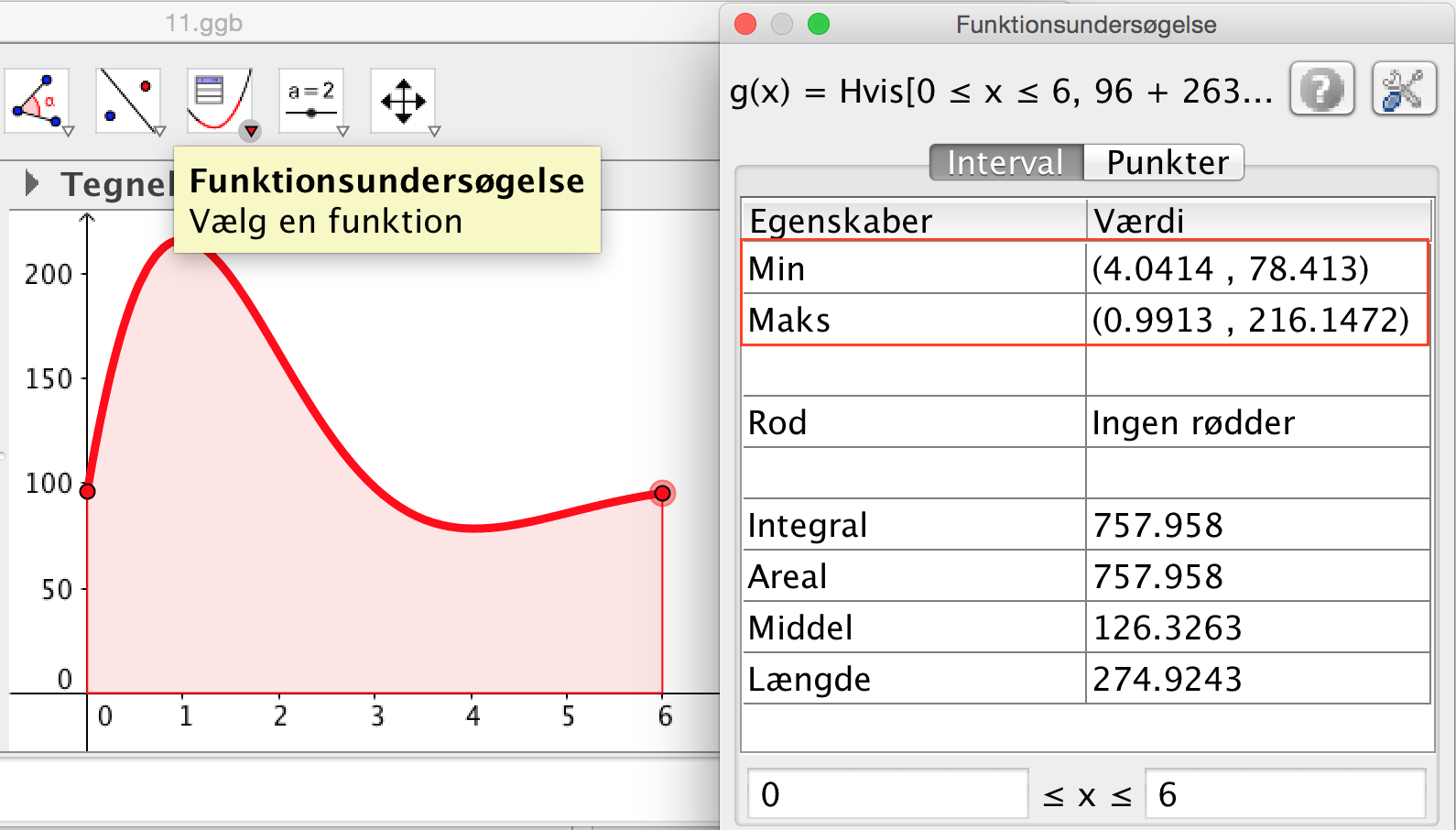
   Geogebra:

   funktionsundersøgelses-værktøjet bruges til at finde minimum og maksimum. Minimum = 78,4 mg/dl og maksimum = 216,1 mg/dl

   

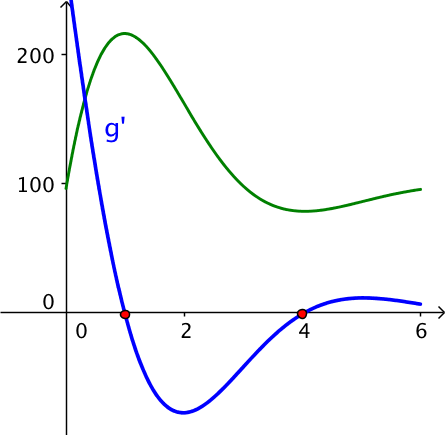
3. Nedenstående figur, der er lavet i Geogebra, viser G'(t) med blå streg. Der er to nulpunkter for G'(t) : et ved maksimum og et ved minimum. Mellem disse værdier er G'(t) < 0 og G(t) dermed aftagende. Dvs. G(t) er aftagende mellem t = 1,0 timer og t = 4,0 timer

   

Svar på opgave 12:

Løsning i Geogebra.

1. Nulhypotesen er, at afvigelserne mellem observerede og forventede hyppigheder skyldes tilfældigheder.

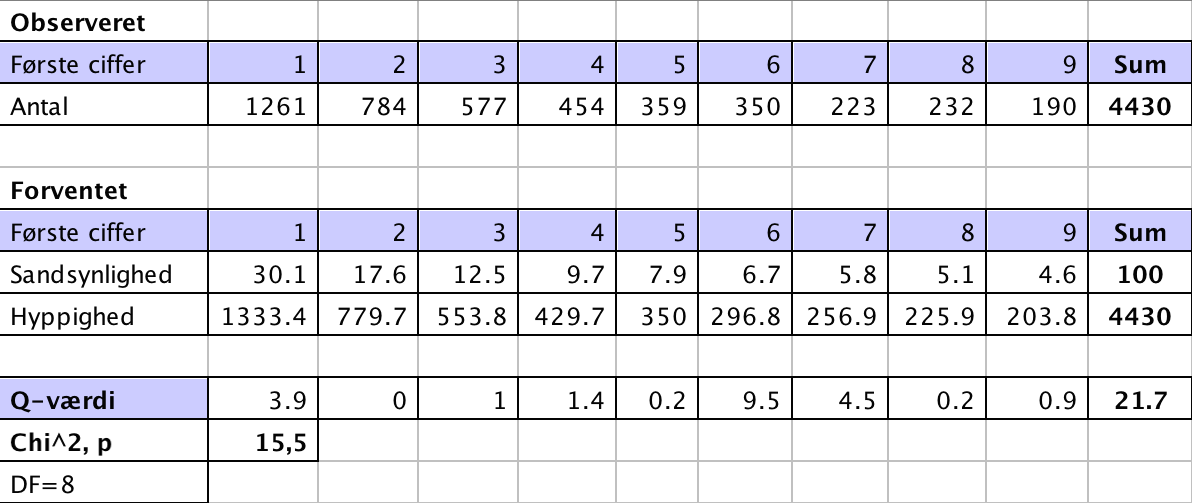
   Der er tale om en goodness-of-fit test, idet man får opgivet forventede sandsynligheder. Disse tal (divideret med 100) ganger man det samlede antal observationer for at finde forventede hyppigheder. Resultatet er vist i tabellen nedenunder.

   

2. Af tabellen fremgår det, at Q-værdien er 21,7. Dette sammenlignes med tallet 15,5, der er nedre grænse for det kritiske område (P(X ≥ 15,5) = 0,05, for en Chi^2 fordeling med 8 frihedsgrader). Da 21,7 ligger i det kritiske område, forkastes nul-hypotesen

Svar på opgave 13:

Løsning i Geogebra.

1. Man indtaster punkterne og bruger Flade gennem 3 punkter-værktøjet.

   

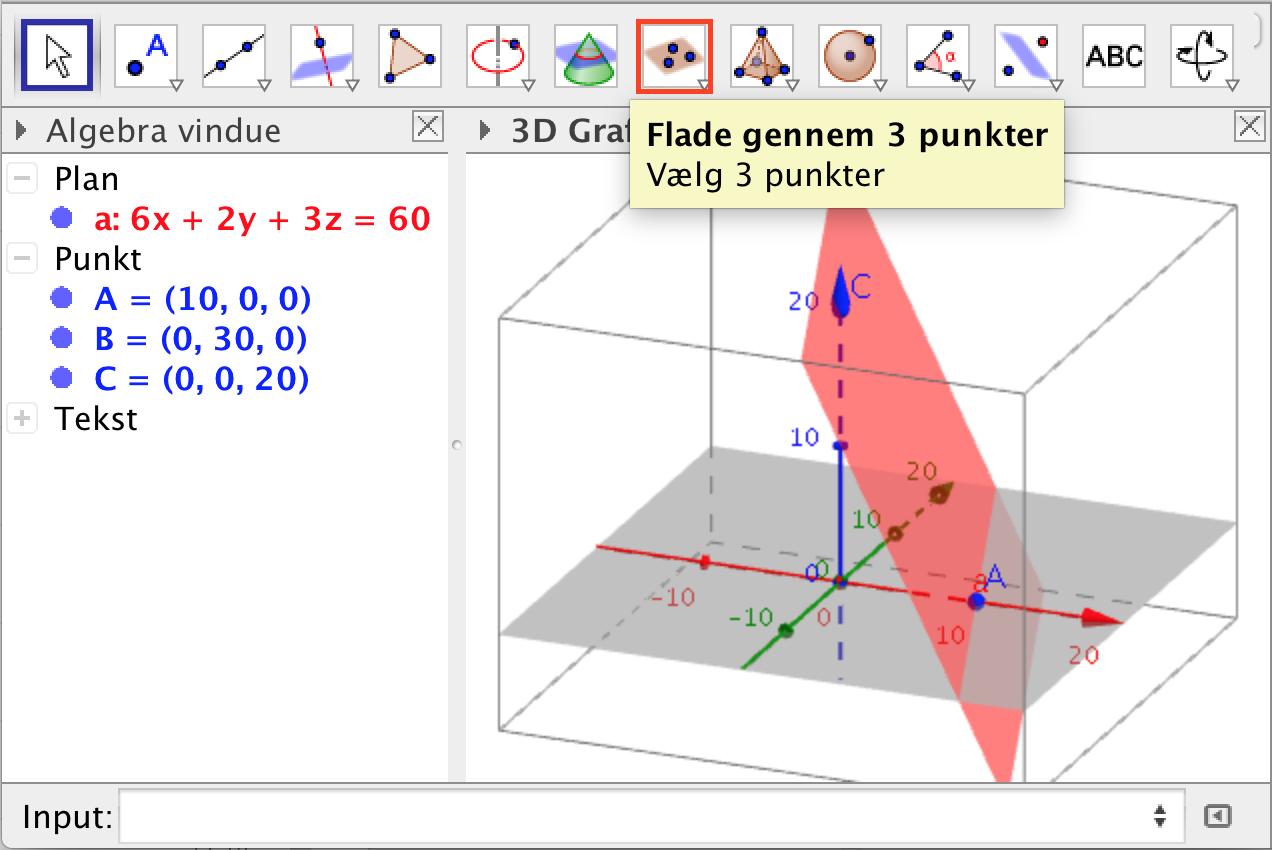
2. Man indtaster punkterne D og E. Man vælger linje-værktøjet (1. i rød ramme fra venstre) og klikker på de to punkter. Dermed får man linjen med det automatisk valgte navn b, der svarer til l. Den har parameterfremstillingen: (x,y,z) = (6,-2,9) + t·(1,-5,1), t er et reelt tal.

   Skæringspunktet F findes ved hjælp af skæringsværktøjet (2. i rød ramme fra venstre). Man klikker først på planen og dernæst på linjen samtidig med at skæringsværktøjet er aktiveret og får F = (5,3,8)

   

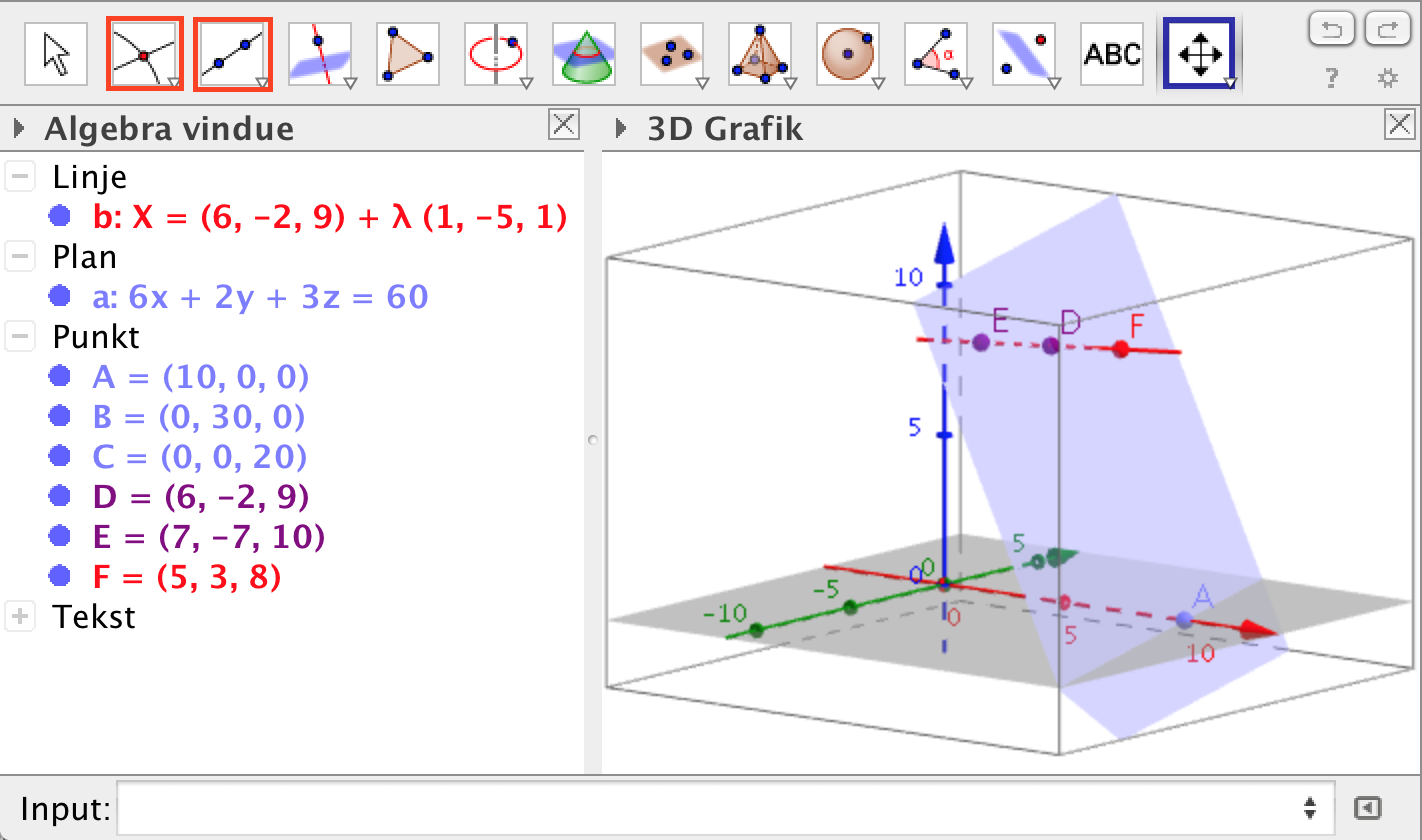
Løsning i Ti-Nspire.

1. AB×AC er normalvektor til planen. Den findes med Ti-Nspire kommandoen:

   

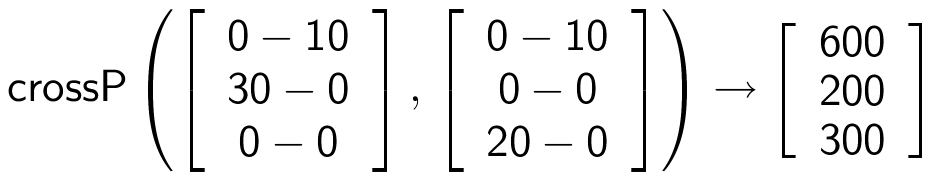
   Et punkt P = (x,y,z) i planen skal opfylde at AP·(AB×AC) = 0. Man findes (AB×AC)·AP ved hjælp af Ti-Nspire kommandoen:

   

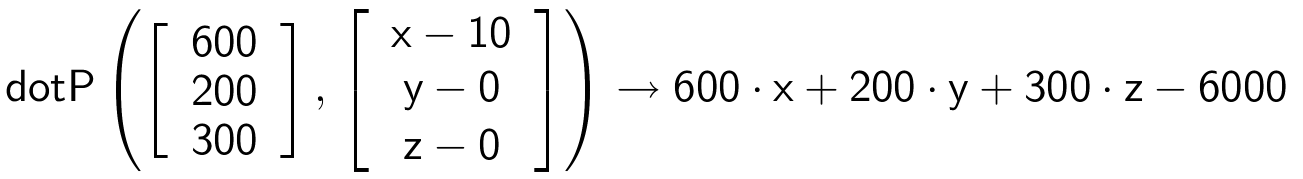
   Dvs. planens ligning er 600x + 200y + 300z - 6000 = 0 eller kortere: 6x + 2y + 3z - 60 = 0

2. Vektoren DE er retningsvektor til linjen. DE = (7 - 6, -7 - (-2), 10 - 9) = (1,-5,1). Linjen går gennem punktet D = (6, -2, 9). Parameterfremstillingen bliver:

   l: (x,y,z) = (6,-2,9) + t·(1,-5,1), t ∈ R.

   Skæringspunktet findes ved først at tage paramterværdierne for x, y og z i linjens parameterfremstilling og indsætte dem i planens ligning.

   Man får: 6x + 2y + 3z - 60 = 0 ∧ (x,y,z) = (6,-2,9) + t·(1,-5,1) ⇔

   6x + 2y + 3z - 60 = 0 ∧ (x = 6 +t ∧ y = -2 -5t ∧ z = 9 + t) ⇒

   6·(6 + t) + 2·(-2 -5t) + 3·(9 + t) - 60 = 0 ⇔

   36 + 6t - 4 - 10t + 27 + 3t - 60 = 0 ⇔ t = -1

   Dette t indsættes i linjens ligning og man finder skæringspunktet: (x,y,z) = (6,-2,9) - 1·(1,-5,1) = (5,3,8)

Svar på opgave 14:

Løsning i Ti-Nspire.

1. Man bruger kommandoerne:

   

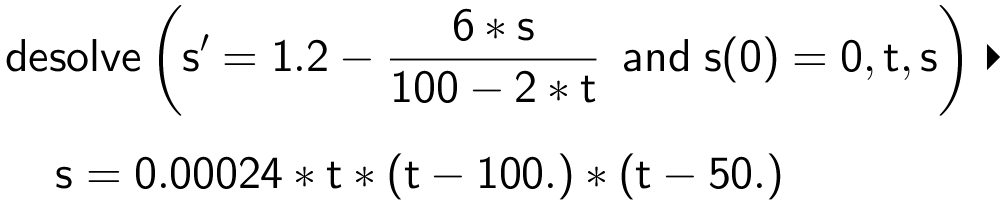
   og

   expand(2.4E^-4*t*(t-100.)*(t-50.)) ▸ 0.00024*t³ - 0.036*t² + 1.2*t

   Løsning: S(t) = 0,00024·t³ - 0,036·t² + 1,2·t, 0 ≥ t ≥ 50

2. Man bruger kommandoen:

   fMax(2.4E^-4*t³-0.036*t²+1.2*t,t)|0≤t≤50 ▸ t=21.13

   Tidspunktet, hvor saltmængden er størst er derfor: t = 21,1 timer

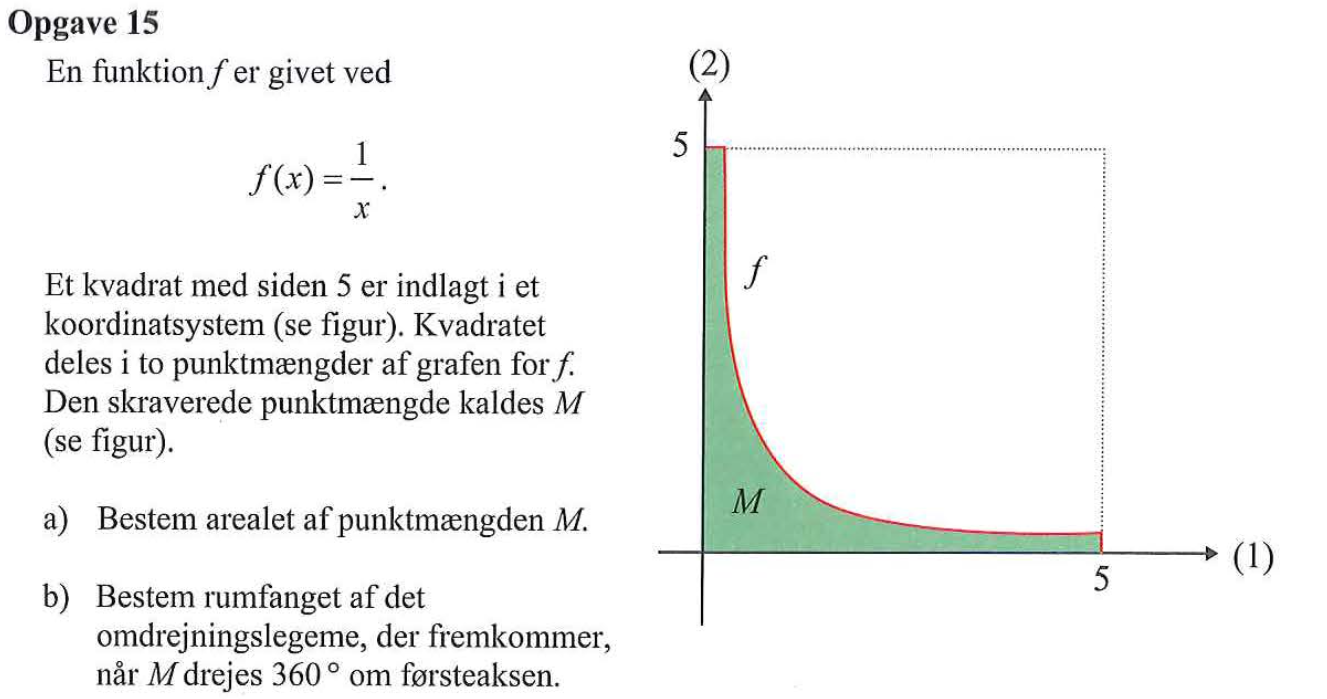
Svar på opgave 15:

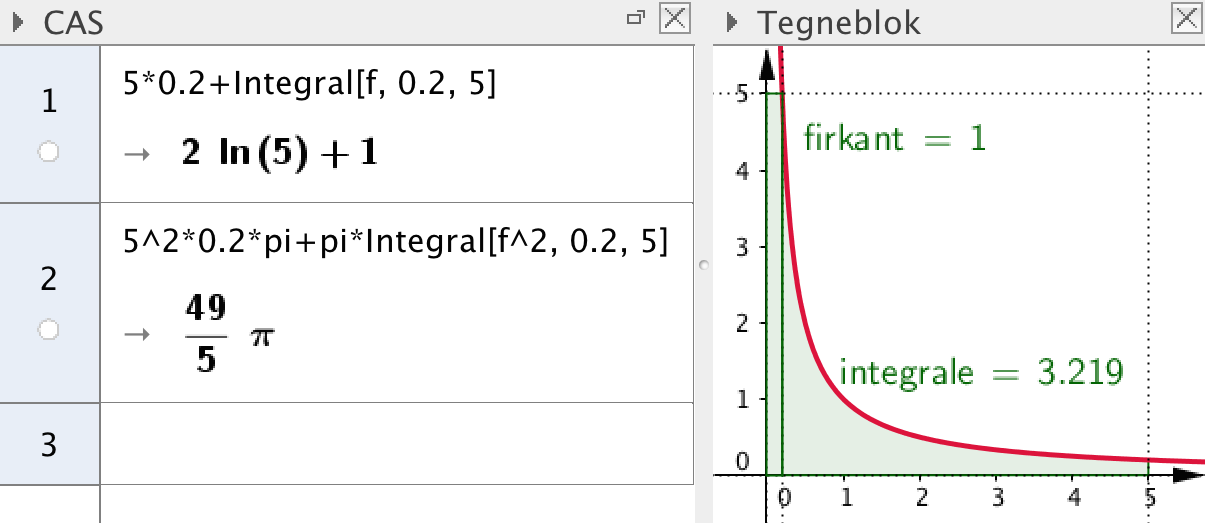
1. Indfør den konstante funktion g(x) = 5. Arealet bliver:

   Areal af rektangel + areal under grafen for f =

   

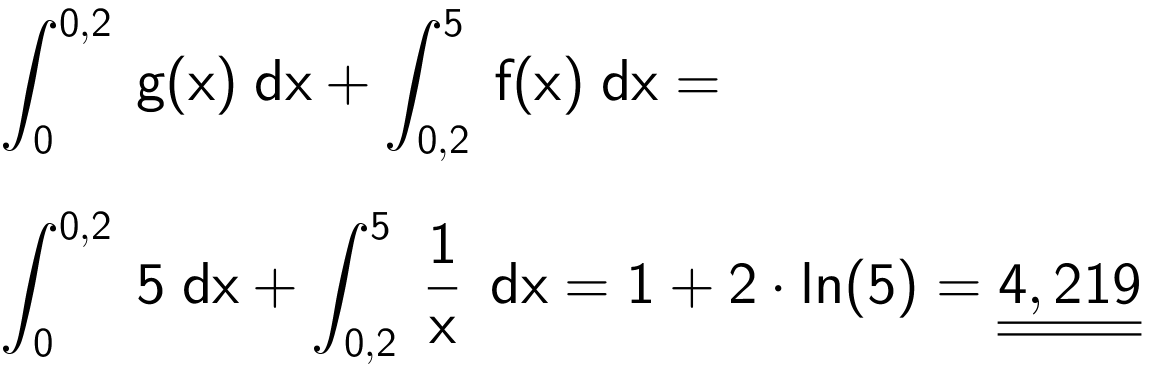
2. Omdrejningslegemet har rumfanget:

   Rumfang af cylinderskive + rumfang af f-grafens omdrejningslegeme =

   

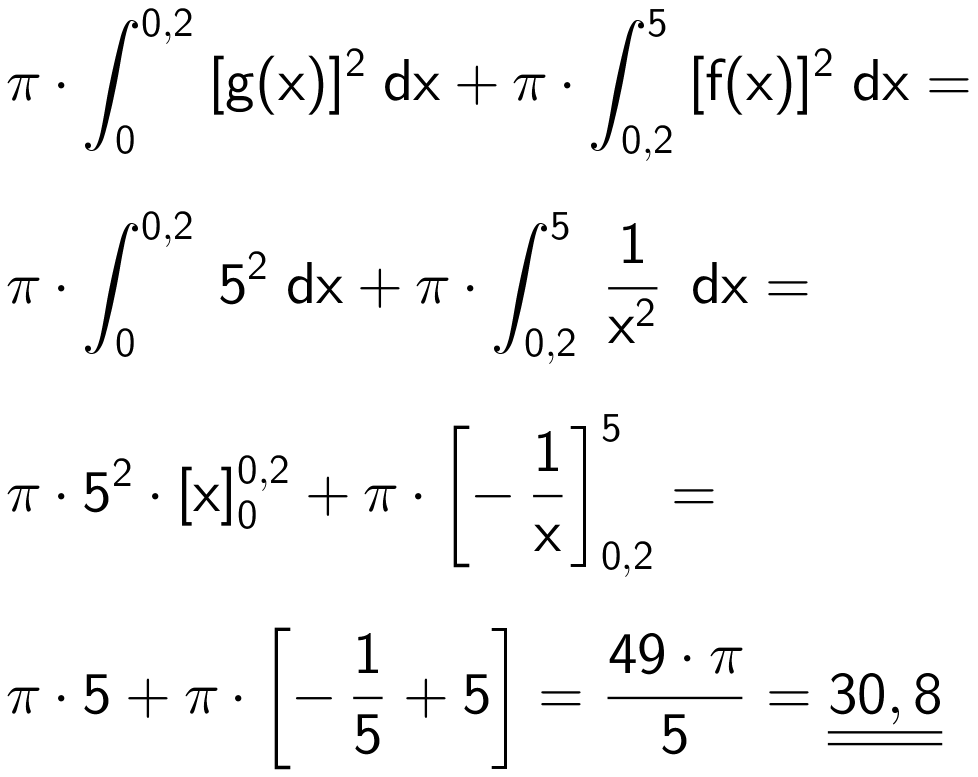
Løsning i Geogebra: