Svar på opgave 1:

1. Variable: x er antallet af år efter 2001, y er antallet af pengeinstitutter.

   Der er tale om en aftagende lineær sammenhæng: y = a·x + b, hvor a er et negativt tal, der viser den årlige nedgang som fast tal. b = y(0) = 190. a = -8.

   Modellen bliver: y = -8·x + 190, hvor 0 ≤ x

   (Da y ikke kan blive negativ, kræves det også, at x ≤190/8 = 23,75.)

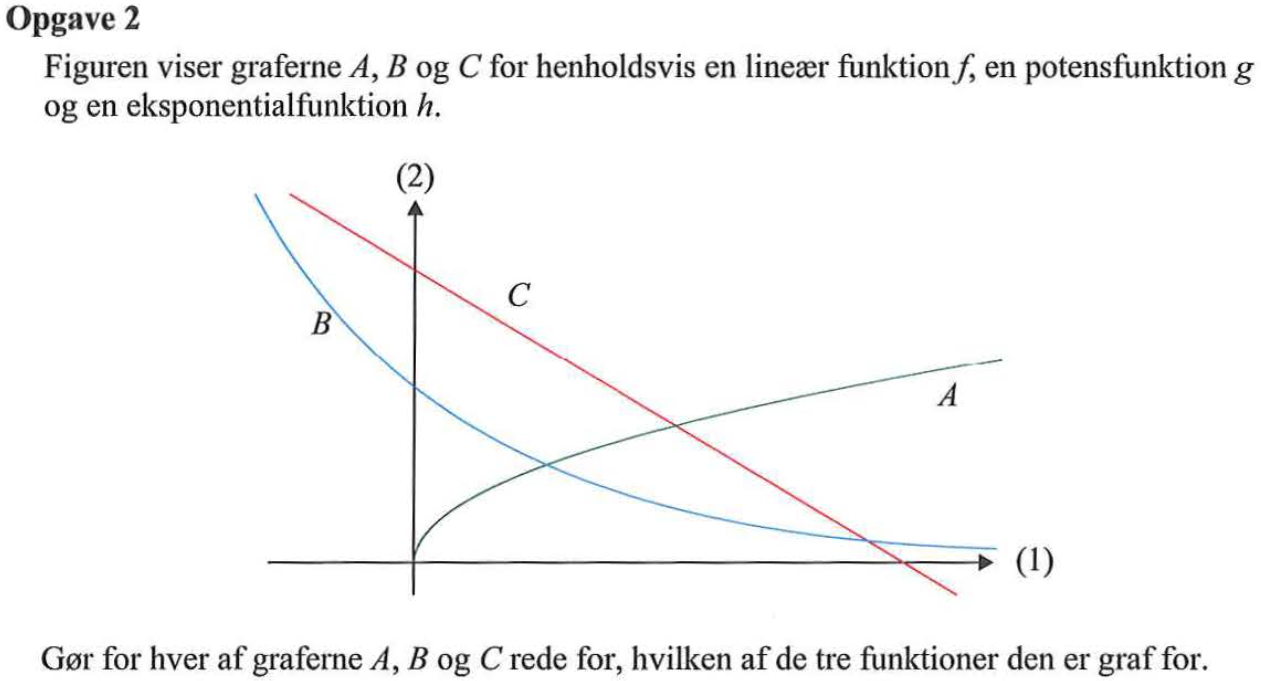
Svar på opgave 2:

1. Den lineære funktion er nemmest at se fordi, den er en ret linje, dvs. C er grafen for f.

   Eksponential-funktionen skærer y-aksen (er defineret for alle x), det gør potensfunktionen ikke (er kun defineret for x > 0). Dermed er A grafen for g og B grafen for h.

Svar på opgave 3:

1. Man skal undersøge om 3³ - 9·3² + 23·3 - 15 er lig med 0. Man får: 3³ - 9·3² + 23·3 - 15 = 27 - 81 + 46 - 15 = 0.

   Svar: 3 er en løsning til ligningen

Svar på opgave 4:

1. Tangentens ligning i (0,f(0)) er: y = f´(0)·(x - 0) + f(0).

   f´(x) = 5·e^x. Man får ligningen: y = 5·e⁰·x + (5·e⁰ + 4) ⇒ y = 5x + 9

Svar på opgave 5:

1. h(x) er stamfunktion til f(x), idet h(x)' = [5·ln(x) + x²]' = 5·[ln(x)]' + [x²]' = 5/x + 2·x = f(x)

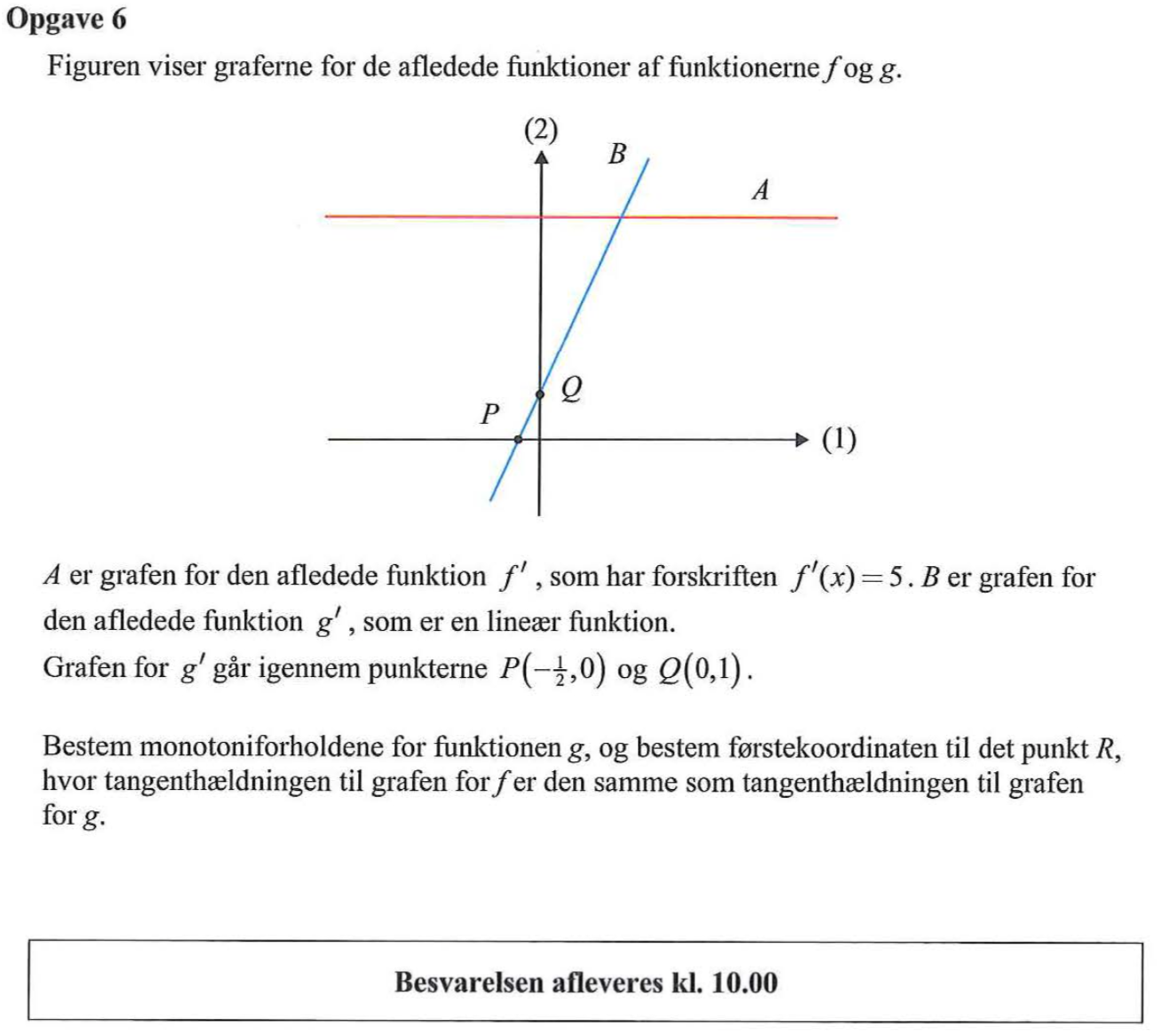
Svar på opgave 6:

1. g' er negativ for x < -1/2 og positiv for x > -1/2, dvs. g er aftagende for x < -1/2 og voksende for x > -1/2

   Tagenthældningen til g skal være 5 , dvs. man skal finde x så g'(x) = 5. Da g' er en lineær fuktion, der går gennem punkterne (-1/2,0) og (0, 1) har den hældningen (1 - 0)/(0 - (-1/2)) = 2. Den skærer y-aksen i y = 1. Dette giver: g'(x) = 2x + 1. g'(x) = 5 ⇒ 2x + 1 = 5 ⇒ x = 2. Førstekoordinaten til R = 2

Svar på opgave 7:

Løsning i Geogebra:

1. Punktet P's koordinater "(5,4)" skrives ind i input-feltet. Det samme gøres med ligningen for l: "x - y + 2 = 0".

   

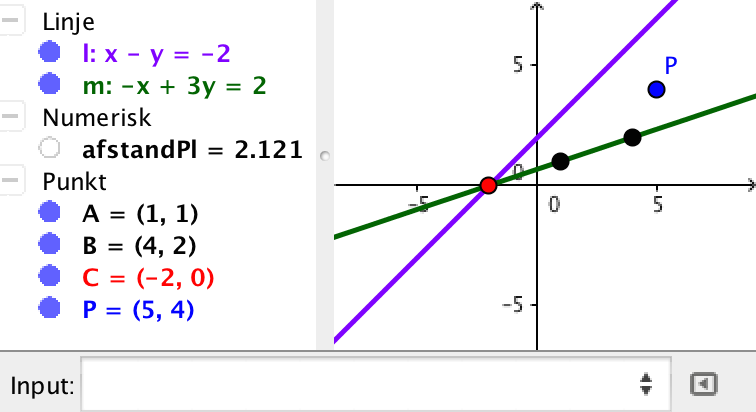
   Afstanden mellem P og l findes til 2,121 ved hjælp af afstandsværktøjet.

2. Parameterfremstillingen for m kan ikke skrives direkte ind. I stedet for indsætter man "(1,1)" og "(4,2)", der er punkterne på m for t = 0 henholdsvis t = 1. Gennem disse punkter oprettes m ved hjælp af linje-værktøjet.

   Ved hjælp af skæringsværktøjet findes skæringen mellem l og m til (-2,0)

Løsning i hånden:

1. Man har: l: 1·x + (-1)·y + 2 = 0 og P = (5,4).

   Afstandsformlen giver: afstand(P,l) = |1·5 + (-1)·4 + 2|/√[1² + (-1)²] = 3/√2 = 2,121

2. Skæringspunktet (x,y) skal opfylde betingelserne:

   1) l : x - y + 2 = 0

   2) m : x = (1 + 3·t) og y = (1 + t)

   Ved at indsætte 2) i 1), så får man løsningen for t:

   (1 + 3·t) - (1 + t) + 2 = 0 ⇒ t = -1

   t = -1 indsættes i 2) og man får skæringspunktet (x,y) = (-2,0)

Svar på opgave 8:

Løsning i Ti-Nspire.

1. Man to lister: en kaldet aarstal med antal år efter 2006 og en kaldet omsaetning, der indeholder omsætningen i mio.

   aarstal:={0,1,2,3,4,5} ▸ {0,1,2,3,4,5}

   omsaetning:={329,434,607,909,1502,2030} ▸ {329,434,607,909,1502,2030}

   

   Heraf aflæses: a = 1,459 og b = 306,5 mio. USD

   Bemærk: Ti-Nspire bruger a og b omvendt i forhold til opgaven. Hvis man er i tvivl, kan man få Ti-Nspire til at udskrive funktionsforskriften ved hjælp af kommandoen:

   f1(x) ▸ 306.515*(1.4592)^x

   f1(x) indgår i kommandoen ExpReg aarstal,omsaetning,1: CopyVar stat.RegEqn,f1: stat.results. Hvis der står et andet tal end 1 efter f, så skal man skrive det i stedet for.

2. Man skal løse ligningen f(x) = 10.000.

   f(x):=306.515*1.45924^x ▸ Udført (f(x) defineres)

   solve(f(x)=10000,x) ▸ x=9.22 (ligningen løses)

   Dvs. der går 9,2 år. Dette rundes op til 10, og man får årstallet: 2006 + 10 = 2016

3. Den årlige vækstrate er (1,459 - 1)·100% = 46%

   Fordoblingstiden er ln(2)/ln(1,459) = 1,85 år

Svar på opgave 9:

1. Man skal løse ligningssystemet: f(3) = 100 ∧ f(15) = 50, med hensyn til a og b.

   Det gøres i Ti-Nspire:

   f(x):=b*x^a ▸ Udført

   solve(f(3)=100 and f(15)=50.,a,b) ▸ a=−0.4307 and b=160.50

   f(x) = 160,5·x^-0,4307

2. Man får f(20) = 44,17. Dette resultat findes med Ti-Nspire:

   f(20)|a=-0.4307 and b=160.5 ▸ 44.17 (beregn f(20), når a er -0,4307 og b er 160,5)

   Man bruger formlen for procentvis ændring af potensfunktioner:

   ((1 + r)^a - 1)·100% = ((1 + 70%)^-0,4307 - 1)·100% = (1,70^-0,4307 - 1)·100% =

   −20.4%, dvs. f(x) falder med 20,4%.

Svar på opgave 10:

1. Løsning i Ti-Nspire:

   f(x):=x⁶-5*x³+4 ▸ Udført

   solve(f(x)=0.,x) ▸ x=1. or x=1.5874

   Dvs.: x = 1 ∨ x = 1,587

2. Man skal finde nulpunkter og fortegn for f´(x). Det gøres i Ti-Nspire:

   1) solve(derivative(f(x),x)<0.,x) ▸ x≠0. and x<1.3572

   2) solve(derivative(f(x),x)>0.,x) ▸ x>1.3572

   3) solve(derivative(f(x),x)=0.,x) ▸ x=0. or x=1.3572

   Af 1) og 3) ses, at f´(x) ≤ 0 for x < 1,3572, mens det af 2) ses, at f´(x) > 0 for x > 1,357. Dvs.:

   f(x) er aftagende (men ikke strengt aftagende) for x < 1,357 og voksende for x > 1,357

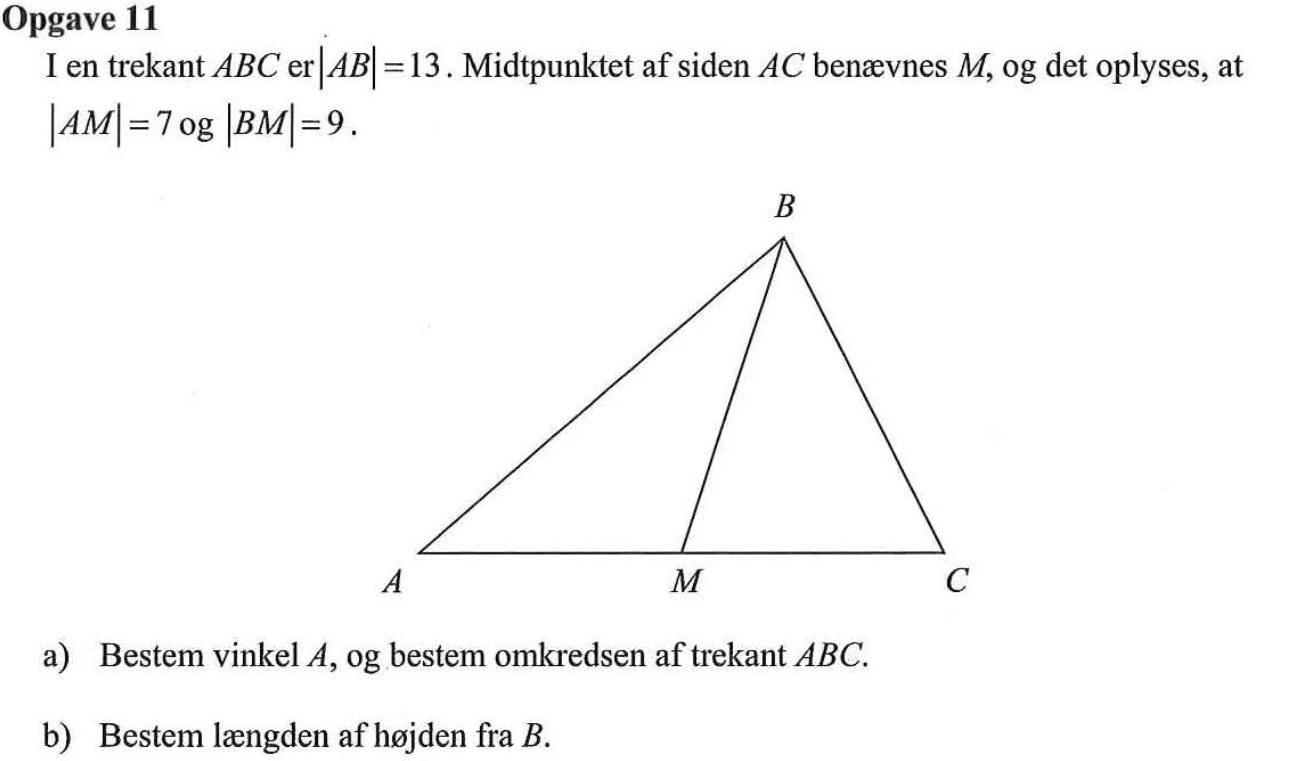
Svar på opgave 11:

Løsning i Geogebra: (konstruktionsforklaring udeladt)

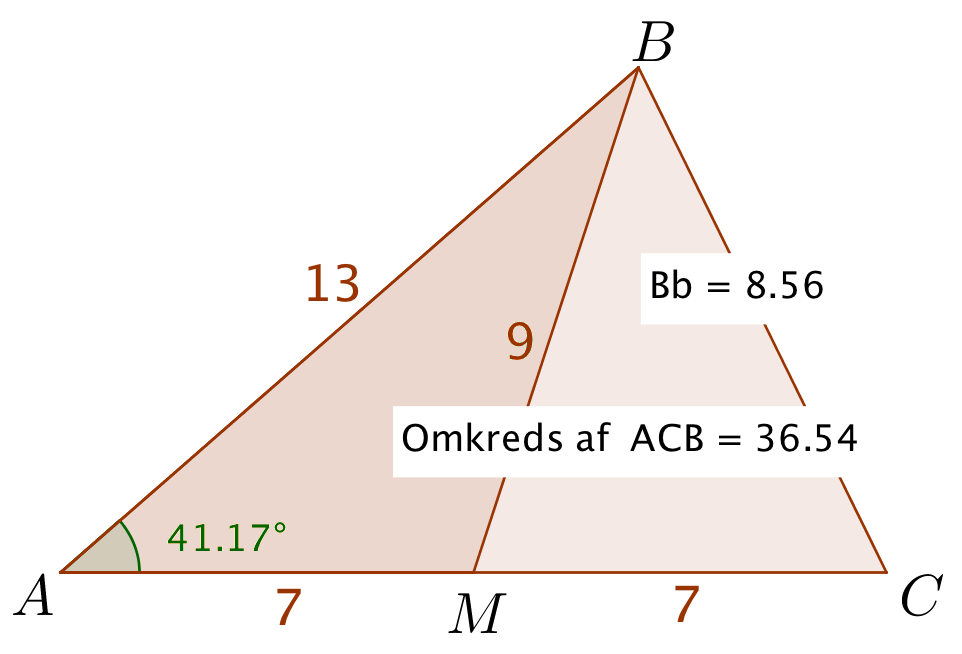
Man aflæser værdierne:

1. ∠A = 41,2°. Omkreds af ABC = 36,5

2. Højden fra B til b er 8,56

Beregnet i hånden:

1. Man bruger cosinusrelationen til at finde vinkel A:

   

   For at finde omkredsen, skal man finde |BC|. Den findes igen ved hjælp af cosinusrelationen:

   

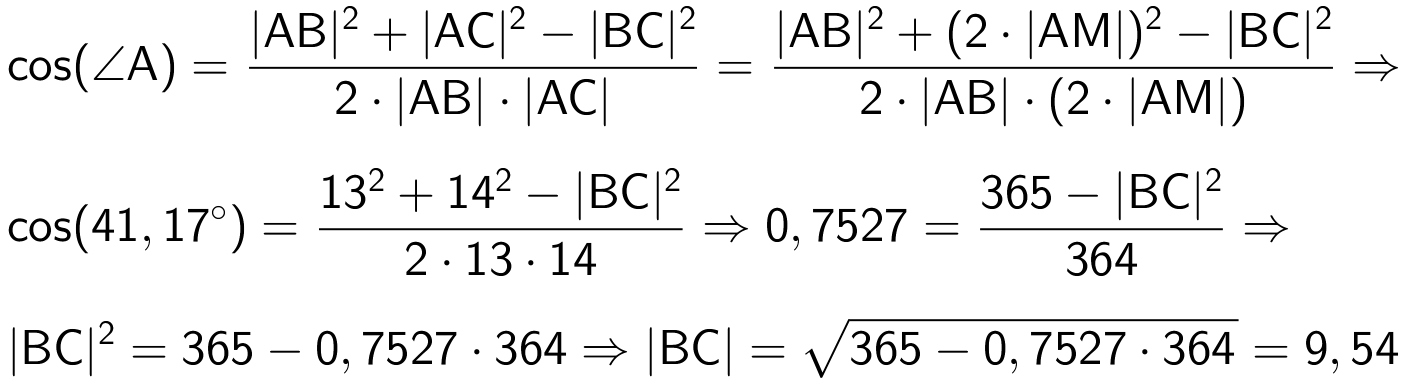
   Omkredsen bliver: 13 + 9,54 + 2·7 = 36,5

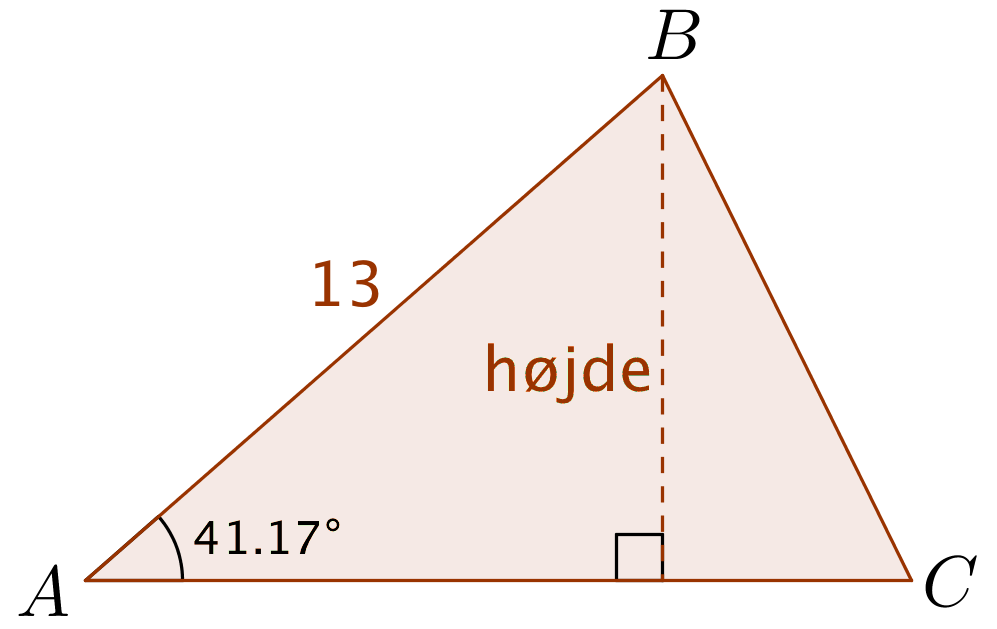
2. Man bruger formlen højde = 13·sin(41,17°) ⇒ højde = 8,56

   

Svar på opgave 12:

Løsning i Geogebra med regneark.

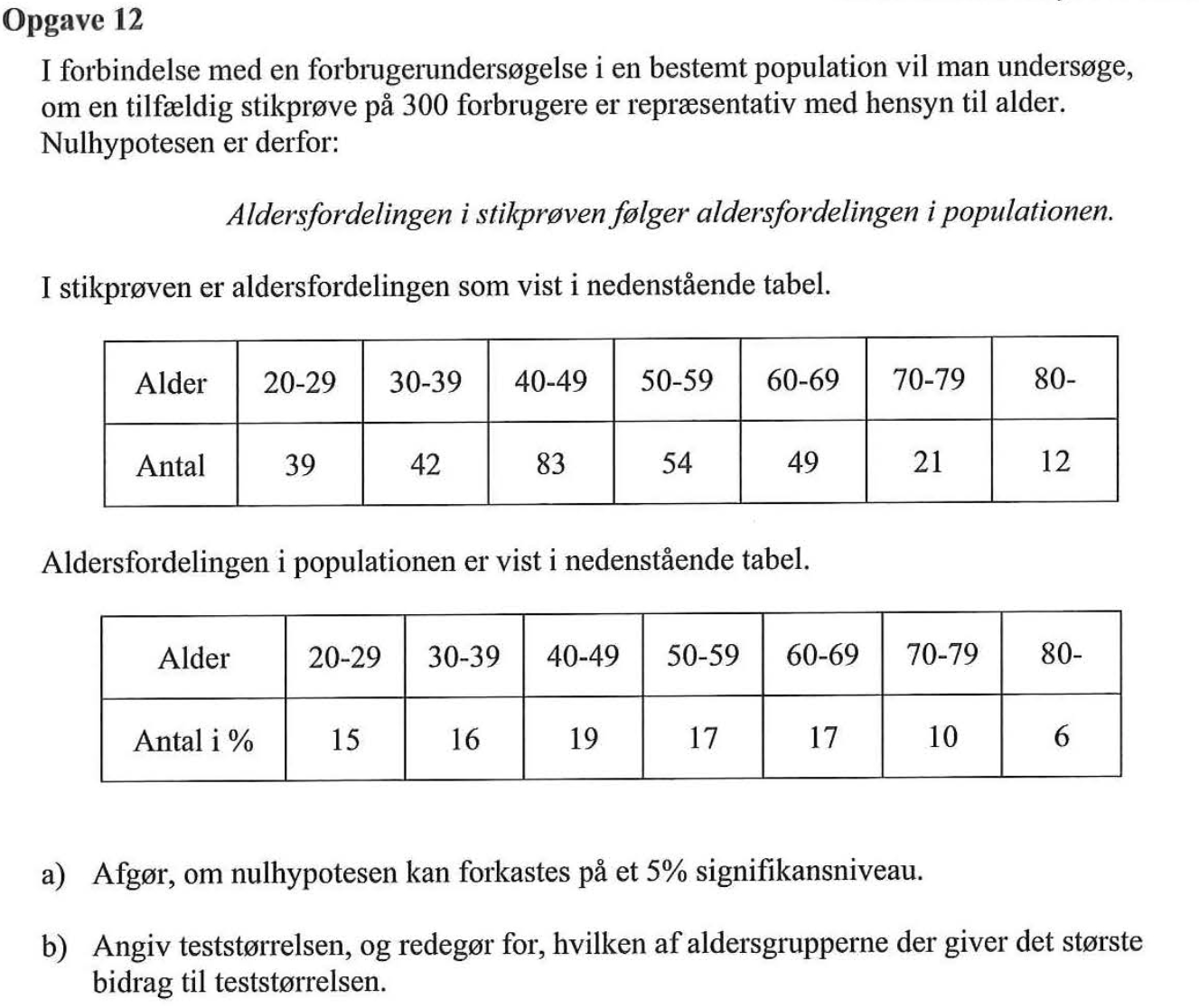
1. Der er tale om GOF, idet man sammenligner et antal med nogle procentdele. Man ordner data i et skema som vist nedenfor. Det forventede antal er summen af observerede antal (300) gange forventede antal i % gange 100.

   

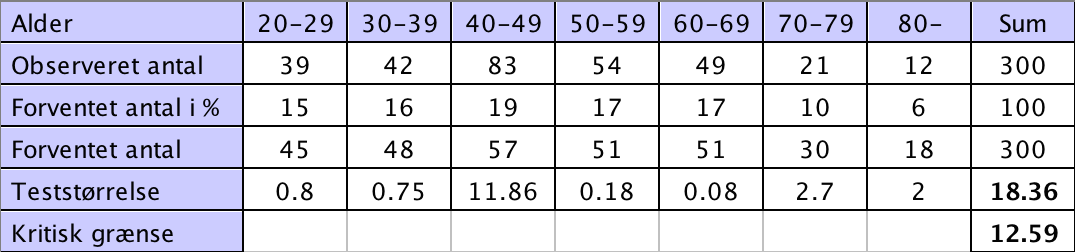
   Den kritske grænse er fundet ved hjæp af Geogebra sandsynligheds­lommergner (den værdi som en stokastisk variabel har 5%'s sandsynlighed for at ligge over med den anvendte sandsynligheds­fordeling).

   Der er brugt en Chi-i-anden fordeling med 6 frihedsgrader (antal aldersgrupper minus en):

   

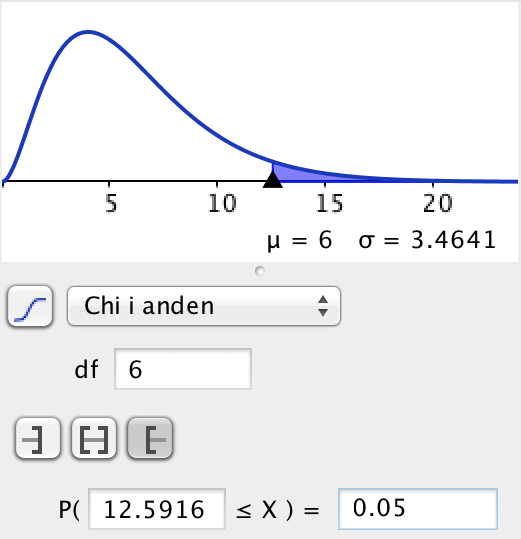
   Teststørrelsen er større end den kritiske grænse, så nul-hypotesen forkastes

2. Teststørrelsen er 18,36 og aldersgruppen 40-49 det største bidrag til den (11,86)

Løsning i Ti-Nspire uden brug af regneark.

1. Man opretter en liste med observerede værdier:

   observeret:={39,42,83,54,49,21,12} ▸ {39,42,83,54,49,21,12} ("observeret" er navnet på listen, hvis enkelte led adskildt af komma)

   En liste med forventede værdier (kaldet "forventet") beregnes ved at gange summen af antallet af observerede værdier med de enkelte forventede procenttal:

   forventet:=sum(observeret)*{0.15,0.16,0.19,0.17,0.17,0.1,0.06} ▸ {45.,48.,57.,51.,51.,30.,18.}

   På disse lister bruger man kommandoen:

   Beregninger ▸ Statistik ▸ Statistiske tests ▸ Χ²-Goodness of Fit test...

   og får:

   χ²GOF observeret,forventet,6: stat.results ▸

   

2. Teststørrelsen fremgår af ovenstående liste ud for χ². Den er: 18,36

   For at finde teststørrelserne for de enkelte aldersgrupper bruger man følgende kommando:

   observeret: stat.CompList ▸ {0.8,0.75,11.86,0.176,0.0784,2.7,2.}

   (Det ses, at tallene på listen svarer til tallene ud for "Teststørrelse" i Geogebra-skemaet ovenfor.)

   På denne liste er det det tredje tal: 11,86, som er det største. Dette gælder for den tredje aldersgruppe: 40-49 år. Man får:

   Aldersgruppen 40-49 det største bidrag til teststørrelsen, nemlig 11,86.

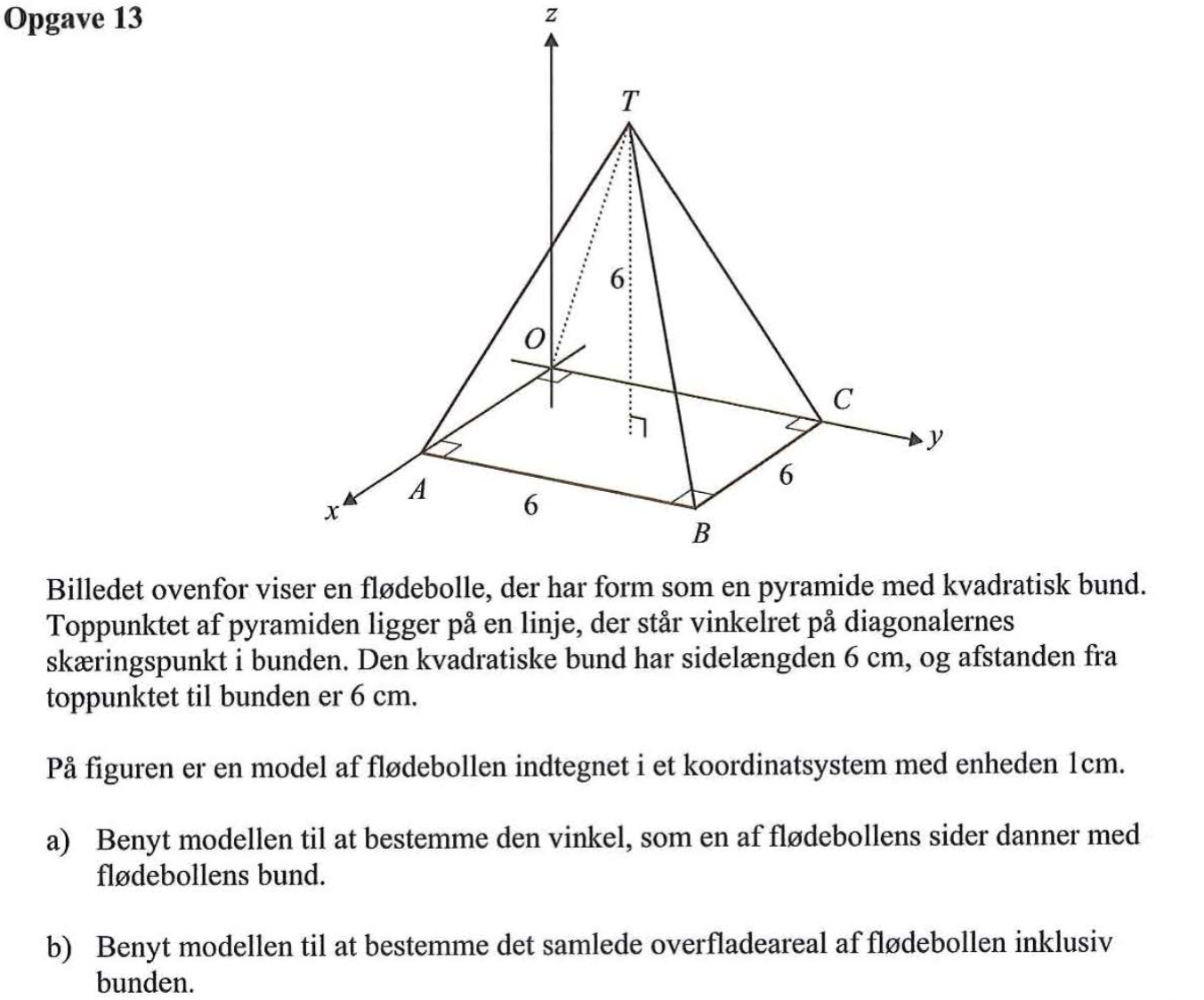
Svar på opgave 13:

Opgaven kan løses alene ved hjælp af plangeometri.

1. Man tegner en trekant RTS som vist nedenunder. R er midtpunktet mellem O og A, og S er midtpunktet mellem B og C (se nedenfor).

   Midtpunktet mellem R og S kaldes P. Dette punkt er også fodpunktet for højden fra T på grundfladen OABC.

   

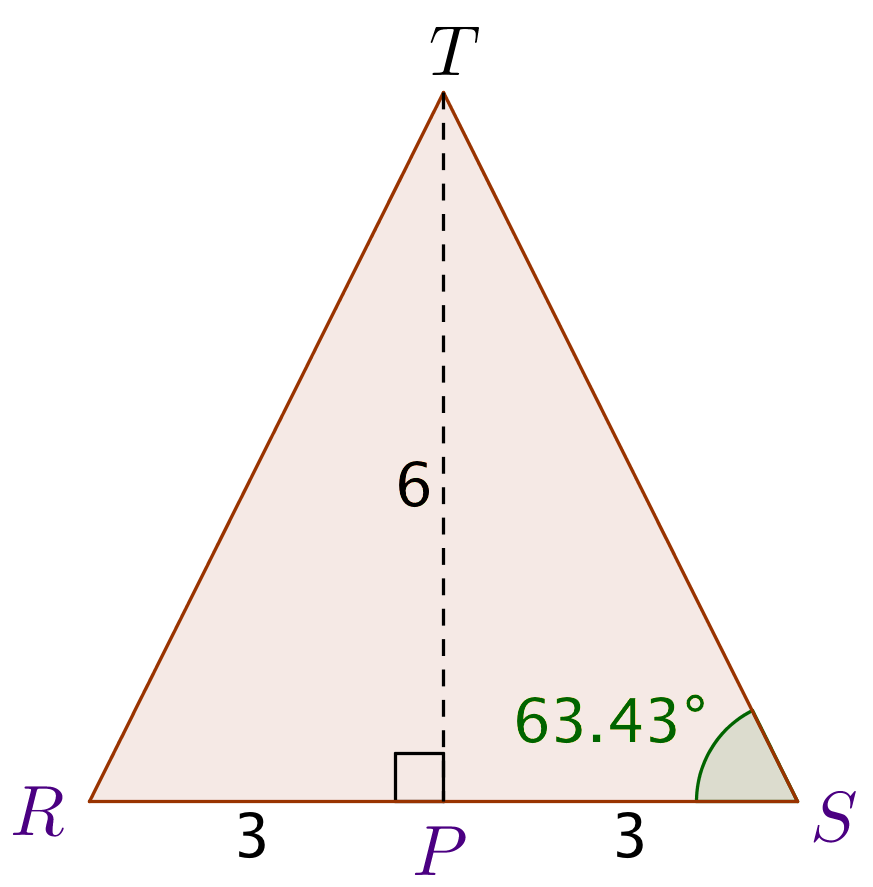
   Den søgte vinkel v kan findes som vinkel S. Der gælder, at |TP|/|PS| = tan(v) ⇒ v = tan^-1 (6/3) = 63,4°

2. Længden |ST| er højden i den ene af fire ens sideflader. Arealet af denne sideflade er ½·6·|ST|. |ST| findes ved hjælp af Pythagoras læresætning og tegningen fra opgave a) til √[6² + 3²] = √[36 + 9] = √45.

   Arealet af en sideflade bliver: ½·6·√45 = 20,12. Det samlede areal af sidefladerne er 4·½·6·√45 = 80,50. Bundfladen er 6² = 36.

   I alt får man følgende overfladeareal af pyramiden: 80,50 + 36 = 116,5

Løsning i Geogebra 3D grafik.

1. Man laver to planer: et ud fra A, B og T (et plan, der indeholder en side) og et ud fra O, A og B (et plan, der indeholder bunden). Man finder vinklen mellem de to planer med vinkelværktøjet.

   

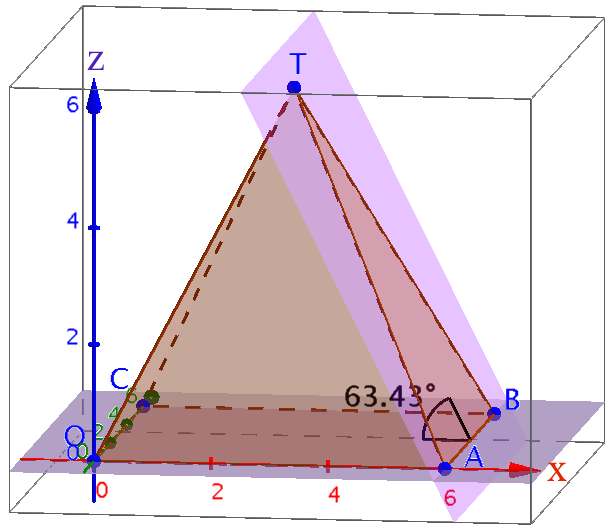
2. Arealet af de enkelte flader er vist til venstre på figuren nedenunder. Trekanten fra 2D løsningen er vist med grønt.

   

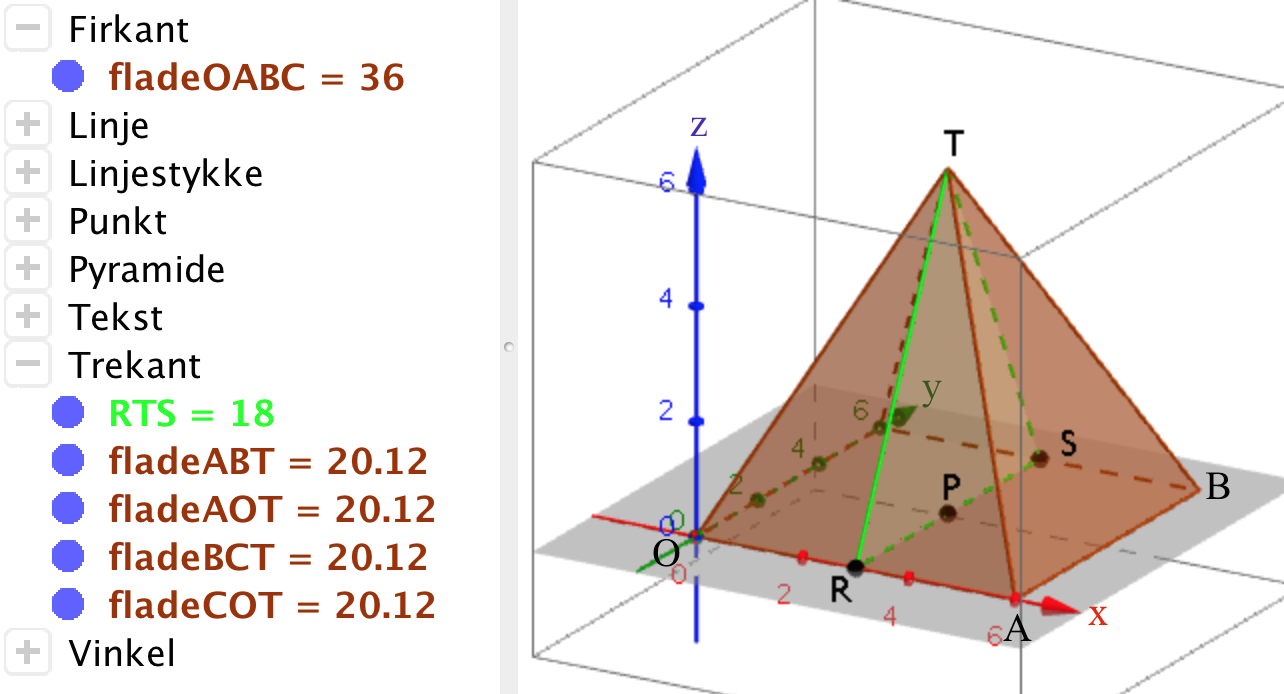
Svar på opgave 14:

1. Området M er vist med brunt på nedenstående tegning, som er lavet i Geogebra.

   

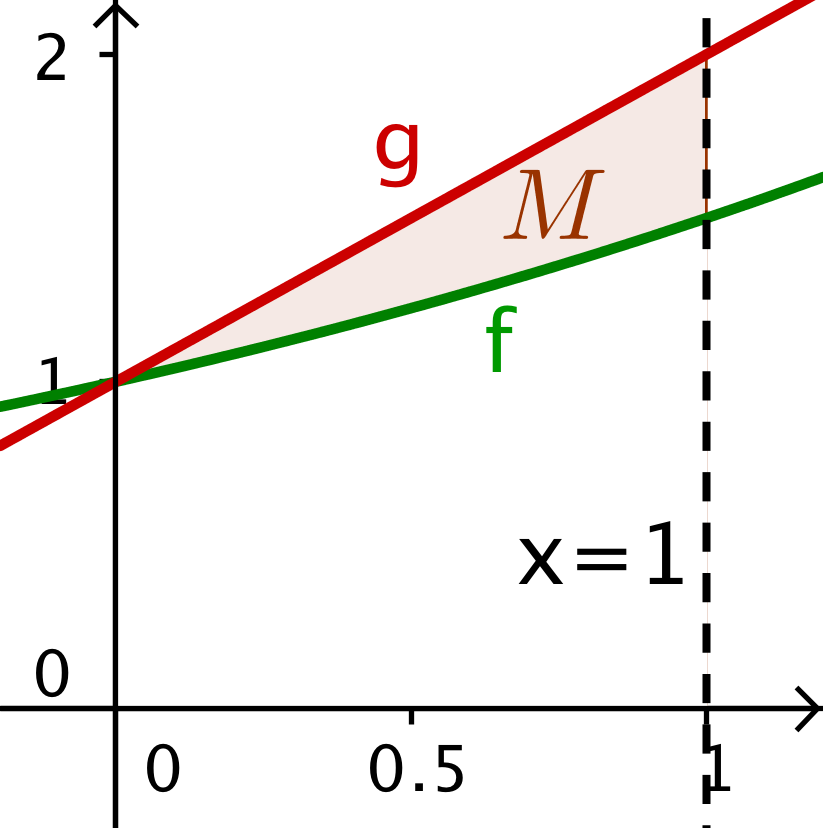
   Arealet af M er:

   

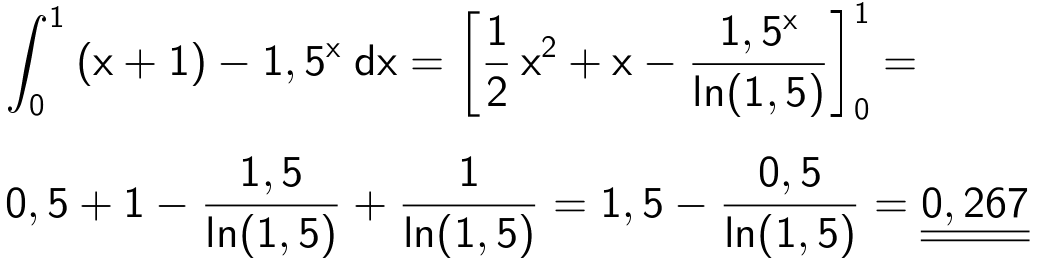
2. Man skal løse nedenstående ligning med hensyn til a (idet det antages, at a > 1):

   

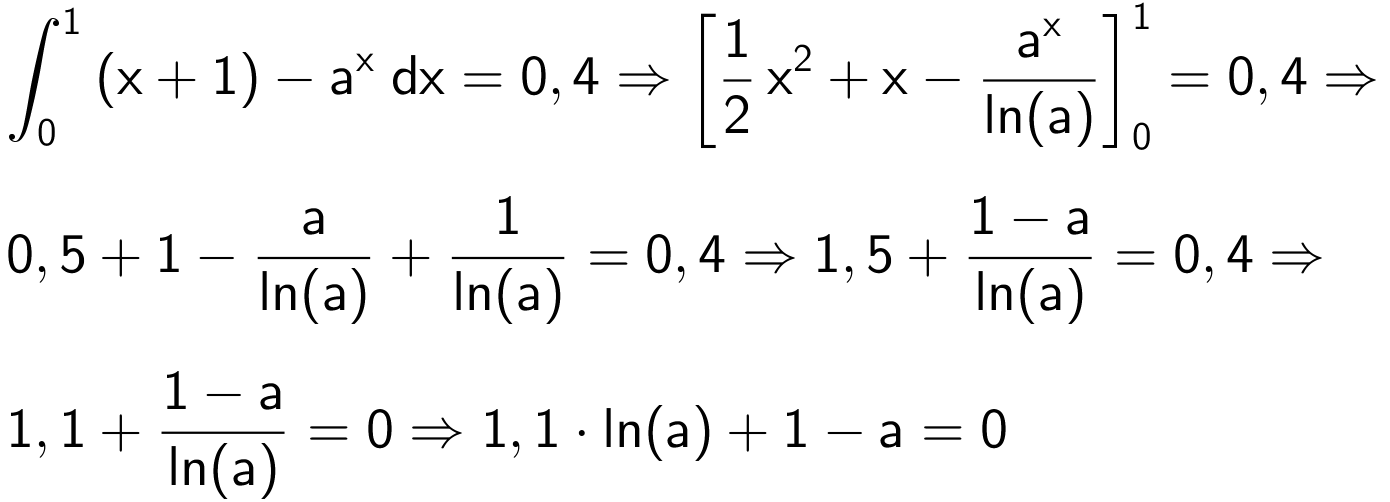
   Dette kan løses som en nulpunktsbestemmelse for funktionen h(x) = 1,1·ln(x) - a - 1.

   I Geogebra får man følgende grafiske løsning, idet den lilla streg er grafen for h(x):

   

   Det ses at skæringspunktet er x = 1,206 (med tre decimalers nøjagtighed) og dermed er værdien af a: 1,206

   I Ti-Nspire løses ligningen ved kommandoen:

   solve(1.1*ln(a) + 1 - a = 0, a) ▸ a = 1. or a = 1.206

   Her er kun a = 1,206 gyldig, da a skal være større end 1.

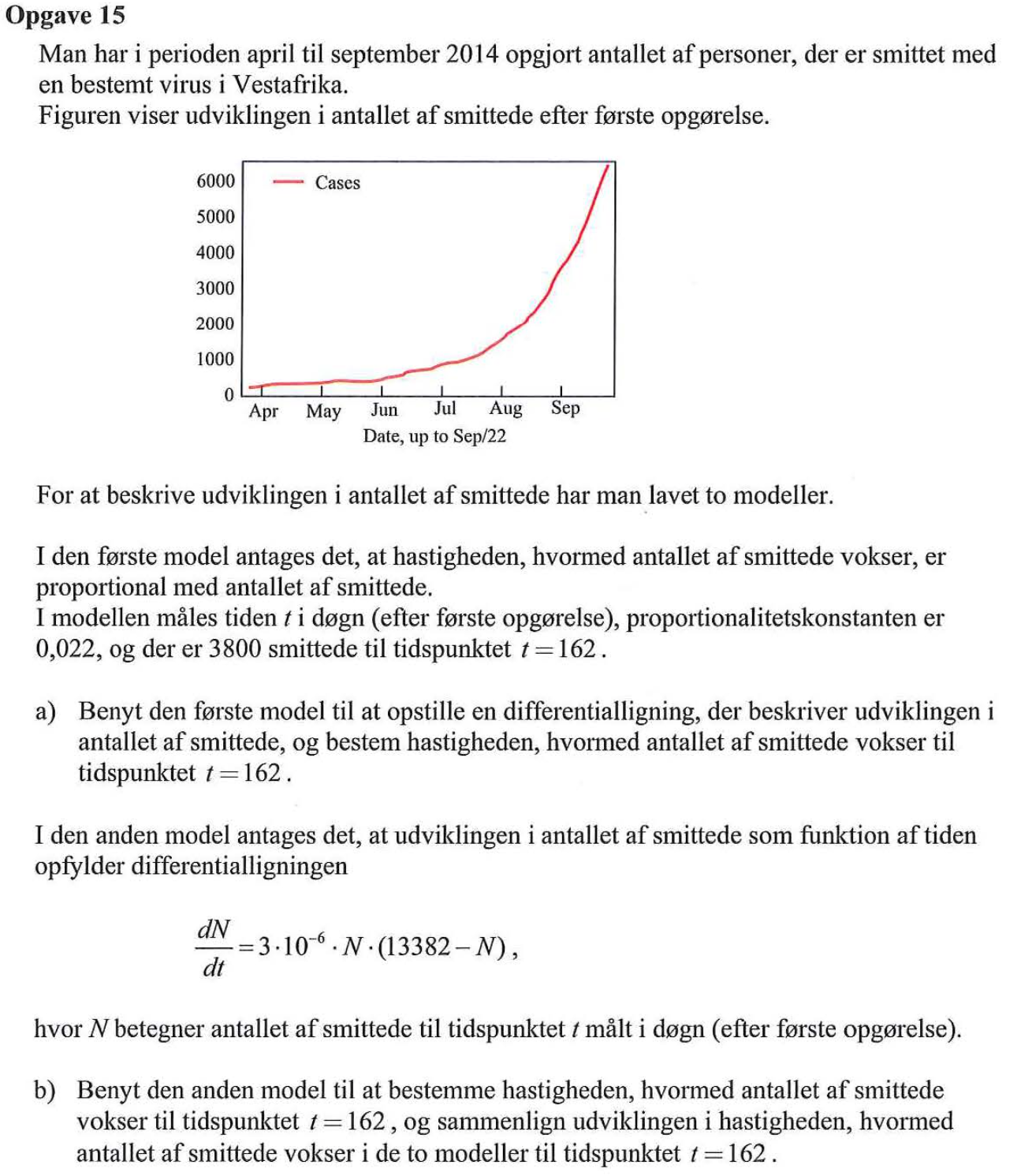
Svar på opgave 15:

Bemærk, at man ikke behøver at løse differentialligningerne for at svare på spørgsmålene, idet der spørges om en hastighed til et givet tidspunkt og ikke et antal. Antallet er i begge tilfælde kendt. For begge modeller gælder: N(162) = 3800.

1. Man får differentialligningen: dN(t)/dt = 0,022·N(t), N(t) > 0, t > 0.

   Man ved at N(162) = 3.800 og får, at væksthastigheden ved t = 162 døgn er lig med: dN(162)/dt = 0,022·N(162) = 0,022·3.800 smittede pr. døgn = 83,6 smittede pr. døgn

2. Væksthastigheden til 162 døgn er:

   dN(162)/dt = 3,0·10^-6·N(162)·(13.382 - N(162)) = 3,0·10^-6·3.800·(13.382 - 3.800) = 109,2 smittede pr. døgn

   Det ses, at antallet af smittede vokser hurtigere til tidspunktet t = 162 døgn med den anden model end med den første.