Svar på opgave 1:

1. Løsning:

   x² + 5x - 14 = 0 ⇔

   x = -5/2 ± (1/2)·√[25 - 4·1·(-14)] ⇔

   x = -5/2 ± (1/2)·√[25 + 56] ⇔

   x = -5/2 ± (1/2)·√81 ⇔

   x = -5/2 ± (1/2)·9 ⇔

   x = -7 ∨ x = 2

Svar på opgave 2:

1. Modellen bliver f(x) = 6·0,987^x,

   f(x) er arealet af havis i mio. km² og x er antal år efter 2008. (0,987 = 1 - 1,3 %.)

Svar på opgave 3:

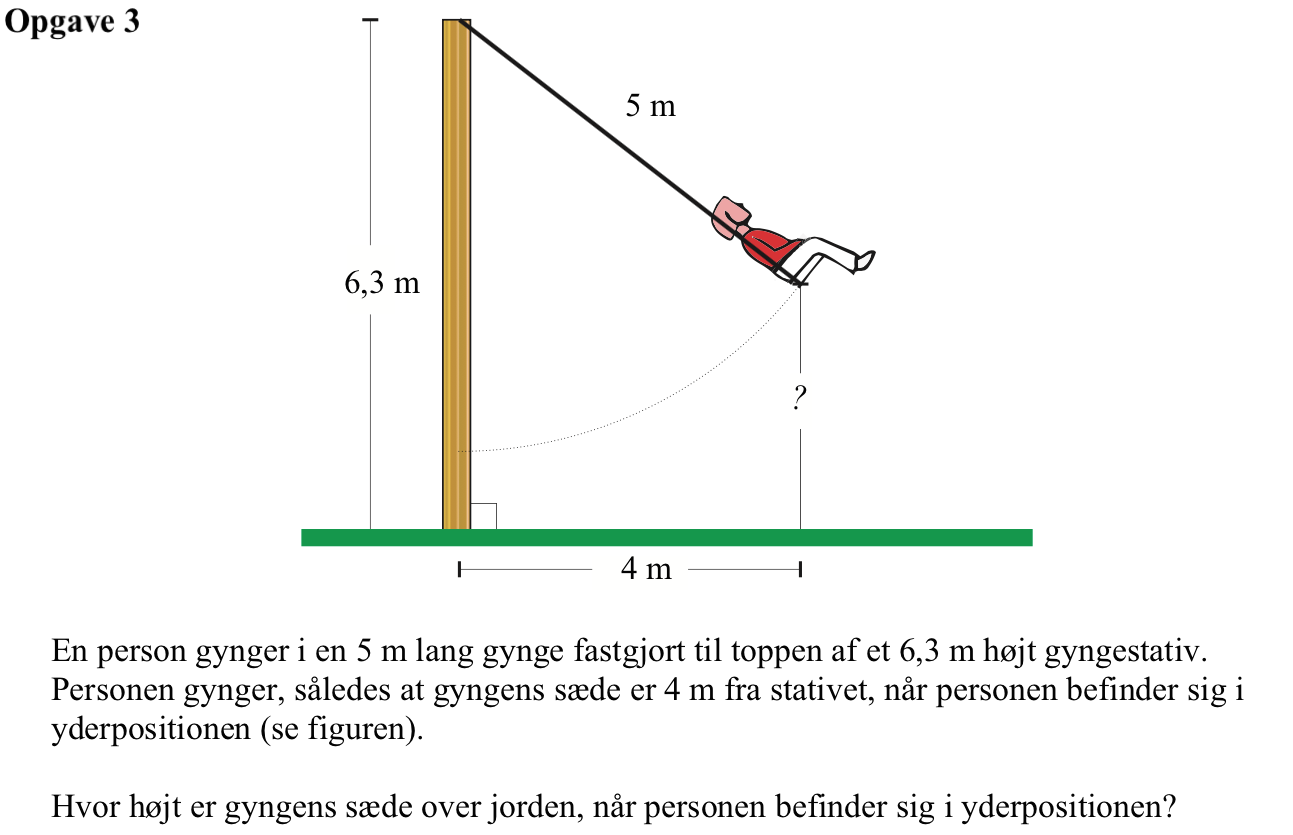
1. Den lodrette afstand fra sædet på gyngen til toppen af stativet kan findes som den korteste katete i en 3-4-5 retvinklet trekant. Dvs. den lodrette afstand fra sædet til toppen er 3 m.

   Disse 3 m skal trækkes fra stativets højde og man får sædets højde over jorden til (6,3 - 3) m = 3,3 m

Svar på opgave 4:

1. Stamfunktionen til f(x) er ln(x) + 2x³ + k.

   Man skal løse ligningen: ln(1) + 2·1³ + k = 8 med hensyn til k:

   ln(1) + 2·1³ + k = 8 ⇔

   2 + k = 8 ⇔

   k = 6

   Dvs. stamfunktionen bliver F(x) = ln(x) + 2·x³ + 6, x > 0

Svar på opgave 5:

1. Tangenten har ligningen: y = ax + b, hvor hældningen a kan findes ved at indsætte (x,y) = (2,3) på højreside af differentialligningen (forudsat der står dy/dx på venstre side og ikke andet):

   (x² + 1)/(y - 1) = (2² + 1)/(3 - 1) = 5/2

   Man har y = (5/2)·x + b

   Derefter findes b ved at indsætte (x,y) = (2,3) i y = (5/2)·x + b og løse den fremkomne ligning med hensyn til b:

   y = (5/2)·x + b ⇒ 3 = (5/2)·2 + b ⇒ b = -2

   Dette giver tangentlignigen:

   y = (5/2)·x - 2

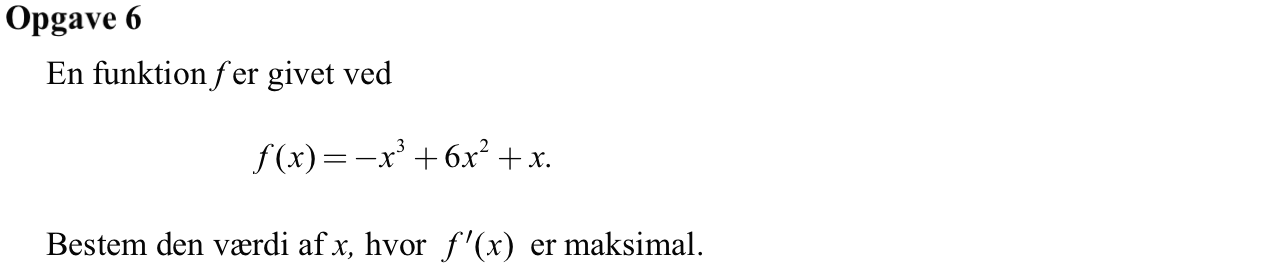
Svar på opgave 6:

1. Da f(x) er et tredjegradspolynomium og man ved at f´(x) har et maksimum, gælder at dette maksimum optræder for det x hvor f''(x) = 0.

   Man har at f´(x) = -3x² + 6x + 1 og f''(x) = -6x + 6

   f''(x) = 0 ⇒ -6x + 6 = 0 ⇔ x = 1

   Dvs. den værdi af x hvor f´(x) er maksimal er x = 1

Svar på opgave 7:

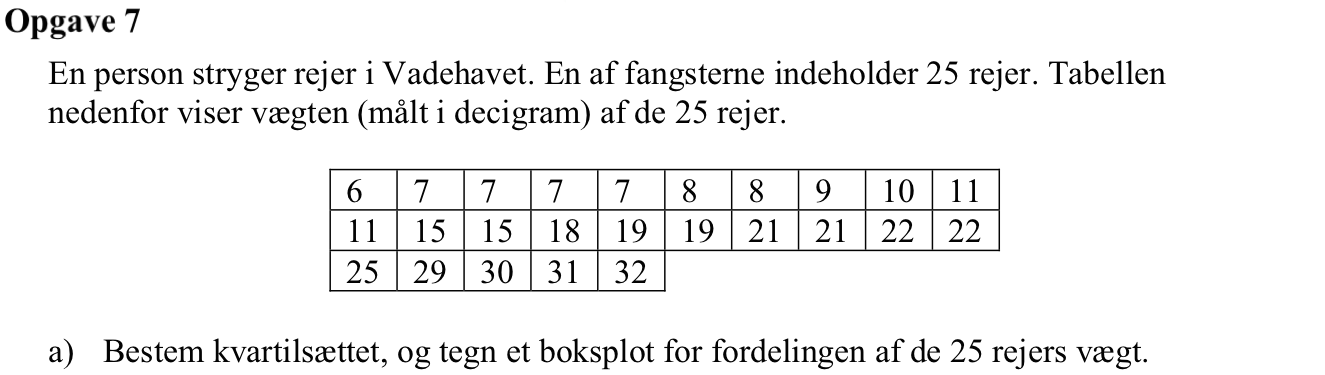
1. Man opretter en liste med vægtene.

   rejevaegt:={6,7,7,7,7,8,8,9,10,11,11,15,15,18,19,19,21,21,22,22,25,29,30,31,32} ▸ {6,7,7,7,7,8,8,9,10,11,11,15,15,18,19,19,21,21,22,22,25,29,30,31,32}

   Ved at bruge kommandoen OneVar rejevaegt,1: stat.results får man en liste over statistiske oplysninger, hvoraf kvartilsættet kan aflæses: 1. kvartil (Q₁X) = 8, median (MedianX) = 15 og 3. kvartil (Q₃X) = 22

   Nedenstående er tegnet i Geogebra:

   

   I Ti-Nspire tegnes boksplot sådan: Man åbner en Tilføj diagrammer og statistik applikation. Man vælger listen rejevaegt på x-aksen. Man højre-klikker på graf-fladen og vælger boxplot.

Svar på opgave 8:

1. Man omskriver ligningen til standardform med kommandoen:

   completeSquare(x²-2*x+y²+2*y-23,x,y)=0 ▸ (x-1)²+(y+1)²-25=0

   Dette kan også skrives: (x-1)² + (y+1)² = 5², som er ligningen for en cirkel med centrum i (1,-1) og radius 5.

2. Man bruger kommandoen:

   solve((x-1)²+(y+1)²-25=0 and x-7*y+17=0,x,y) ▸ x=−3 and y=2 or x=4 and y=3

   Dvs. skæringspunkterne er (x,y) = (-3,2) og (x,y) = (4,3)

Svar på opgave 9:

1. Man deler tabellens data op på to lister:

   temp:={288,298,308,318,328,338,348,358,368} ▸ {288,298,308,318,328,338,348,358,368}

   hast:={340,346,352,357,363,369,374,379,385} ▸ {340,346,352,357,363,369,374,379,385}

   Man bruger kommandoen:

   Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Potensregression... på listerne x=temp og y=hast og får:

   

   f(x) = 19,63·x^0,5037 (Bemærk, Ti-Nspire bruger a og b i omvendt rækkefølge af opgaven).

2. Man bruger formlen for procentvis ændring af potensfunktioner og finder følgende ændring:

   ((1 + r)^a - 1)·100% = ((1 + 5%)^0,5037 - 1)·100% = (1,05^0,5037 - 1)·100% = 2,5 %, dvs. hastigheden vokser med 2,5 %, når temperaturen vokser med 5 %.

Svar på opgave 10:

1. Tegnet i Geogebra:

   

   Arealet af trekanten er 0,5·højde·grundlinje = 0,5·4·10 = 20

2. Der gælder, at |AB|·sin(20°) = højde. |AB| findes ved Ti-Nspire-kommandoen:

   solve(x*sin(20°)=4.,x) ▸ x=11.695

   Dvs. |AB| = 11,7

   Man bruger sinusrealtionen, idet ∠C kaldes x og ∠B dermed bliver 180° - 20° - x. Man får i Ti-Nspire ved hjælp af solve:

   

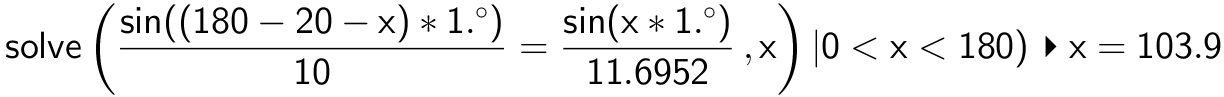
   Dvs. vinkel C = 103,9°

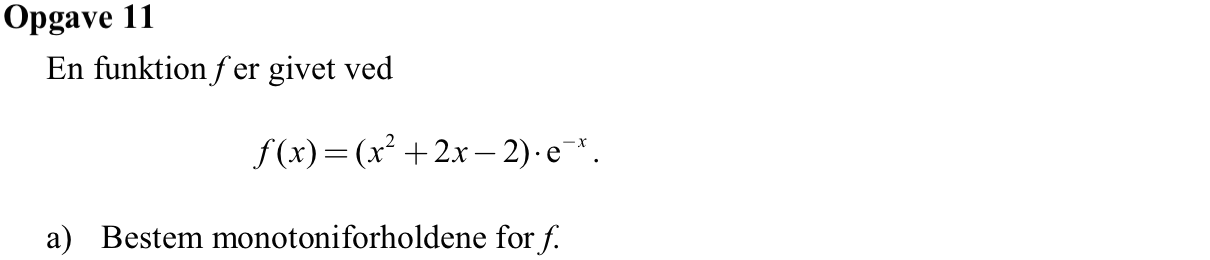
Svar på opgave 11:

1. f(x):=(x²+2*x-2)*exp(−x) ▸ Udført (man definerer f(x))

   solve(derivative(f(x),x)<0,x) ▸ x<−2 or x>2 (man finder de x, hvor f´(x)<0)

   solve(derivative(f(x),x)>0,x) ▸ −2<x<2 (man finder de x, hvor f´(x)>0)

   Man får monotoniforholdene:

   f(x) aftager for x < -2

   f(x) vokser for -2 < x < 2

   f(x) aftager for x > 2

Svar på opgave 12:

1. Tegning i Ti-Nspire (med x i stedet for t):

   

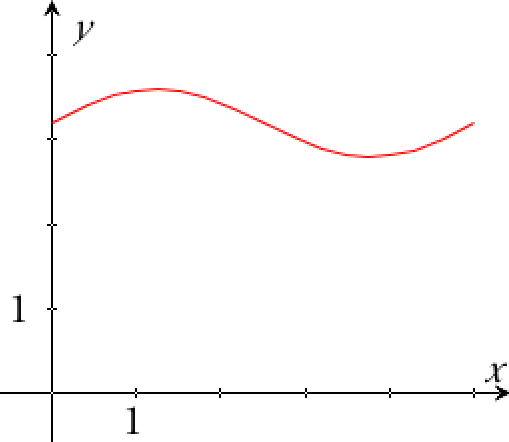
   sinus-funktionen kan højst give værdien 1. Derfor er maksimum for f(x) = 3,2 + 0,4 = 3,6

2. f(t):=3.2+0.4*sin(1.25*t) ▸ Udført (man definerer f(t))

   solve(f(t)=3.5,t)|0≤t≤5 ▸ t=0.6784 or t=1.8348 (man finder de t, hvor f(t) = 3,5)

   De t hvor f(t) er 3,5 er t = 0,68 og t = 1,83

3. derivative(f(t),t)|t=2 ▸ −0.401 (beregning af f´(2))

   Man får at f´(2) = -0,40. Dvs. luftmængden i lungerne aftager med 0,4 liter/sekund til tiden 2 sekunder.

Svar på opgave 13:

1. Nulhypotesen er, at rygevaner og aktivitetsniveau er uafhængige af hinanden.

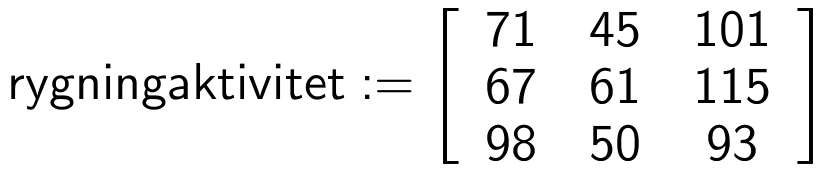   (man definerer matricen)

   

   ...(man udfører en chi-i-anden uafhængighedstest)

   PVal = 0.038324 = 3,8 %. Da dette tal er mindre end 5 % forkastes nulhypotesen.

Svar på opgave 14:

1. f(x):=sqrt(25-((5*x/2.1))²) ▸ Udført (man definerer f(x))

   pi*integral((f(x))²,x,-2.1,2.1) ▸ 219.9 (beregning af rumfang ved rotation om x-aksen)

   Dvs. rumfanget er 219 m³

2. Man får i Ti-Nspire:

   2*π*integral(f(x)*sqrt(1+(derivative(f(x),x))²),x,−2.1,2.1) ▸ 203.28 (bereging af integrale)

   Man får, at husets overfladeareal er 203,3 m²

Svar på opgave 15:

1. Væksthastigheden dh/dt beregnes ved at indsætte h = 4 på højre side af differentialligningen. Man får

   Væksthastighed = dh/dt = 0,16·4 cm/døgn = 0,64 cm/døgn

2. deSolve(h'=0.16*h and h(0)=3,x,h) ▸ h=3.*(1.1735)^x (løsning af differentialligningen med startbetingelsen h(0) = 3 cm)

   solve(8=3.*(1.17351)^x,x) ▸ x=6.13 (man finder det t, hvor h(t) = 8 cm)

   Det ses, at der går 6,13 døgn mellem de to klipninger

Svar på opgave 16:

1. Man opretter punkterne som stedvektorer

   a:=[3,0,0] ▸ [3,0,0]

   b:=[0,5,0] ▸ [0,5,0]

   c:=[0,0,t] ▸ [0,0,t]

   ab:=b-a ▸ [−3,5,0]

   ac:=c-a ▸ [−3,0,t]

   Arealet findes som halvdelen af længden (normen) af krydsproduktet AB × AC for t = 4

   0.5*norm(crossP(ab,ac))|t=4 ▸ 13.865

   Dvs. arealet er 13,9

2. Man finder det t som gør, at skalarproduktet af vektoren (AB + AC) med l's retningsvektor (10,6,15) giver resultatet 0:

   solve(dotP([10,6,15],ab+ac)=0,t) ▸ t=2

   Dvs. den værdi af t, som gør at l står vinkelret på planen som A, B og C ligger i, er 2