Svar på opgave 1:

1. Løsning:

   x² + 2x - 15 = 0 ⇔

   x = -1 ± (1/2)·√[4 - 4·1·(-15)] ⇔

   x = -1 ± (1/2)·√64 ⇔

   x = -1 ± 4 ⇔

   x = -5 ∨ x = 3

Svar på opgave 2:

1. Tallet -2,5 er faldet i antal solgte is ved en prisstigning på 1 kr. pr. is

   Prisen, der betyder, at der ikke længere sælges nogen is, findes som løsningen til ligningen f(x) = 0:

   f(x) = 0 ⇒ -2,5x + 125 = 0 ⇔ x = 50

   Dvs. prisen, hvor der ikke længere sælges nogen is, er 50 kr.

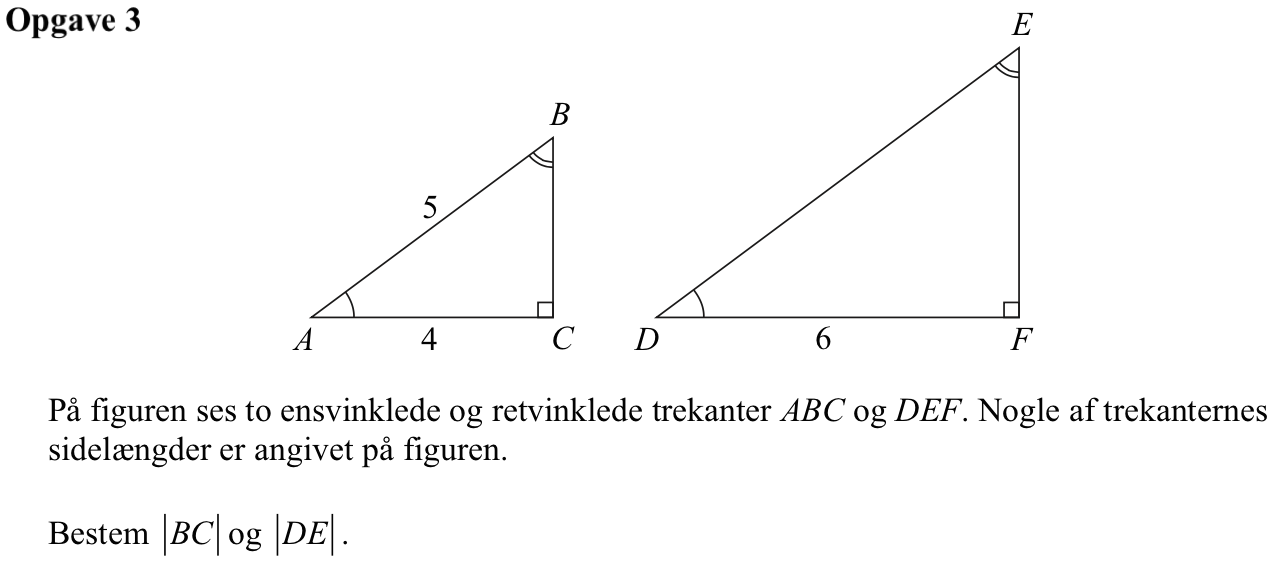
Svar på opgave 3:

1. |BC| findes ved hjælp af Pythagoras læresætning:

   |BC| = √[5² - 4²] = 3

   Skaleringsfaktoren er |DF|/|AC| = 6/4 = 1,5.

   |DE| = 1,5·|AB| = 1,5·5 = 7,5

Svar på opgave 4:

1. Man laver en kvadratkomplettering for at opstille cirklens ligning på standardform:

   x² - 4x + y² + 6y - 3 = 0

   (x - 2)² - 4 + (y + 3)² - 9 - 3 = 0

   (x - 2)² + (y + 3)² = 16 = 4²

   Heraf ses, at cirklens centrum er (2,-3) og radius er 4

Svar på opgave 5:

1. Man skal gøre prøve for at se, om man får det samme på begge sider af lighedstegnet.

   Venstre side: dy/dx = f´(x) = e^x + x·e^x = (1 + x)e^x

   Højre side: y + e^x = f(x) + e^x = x·e^x + e^x = (1 + x)e^x

   Dvs. prøven stemmer og f(x) er en løsning til differentialligningen.

Svar på opgave 6:

1. Man bruger substitutionen: y = x³ - 7,

   dy/dx = 3x² ⇒ dy = 3x²dx,

   y_start = (x_start)³ - 7 = 2³ - 7 = 1,

   y_slut = (x_slut)³ - 7 = 3³ - 7 = 20

   Man får det omskrevne integrale:

   

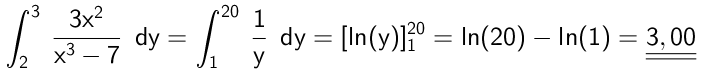
Svar på opgave 7:

Løsning i Ti-Nspire.

Vektorerne oprettes:

a:=[−1,3] ▸ [−1,3]

b:=[2,5] ▸ [2,5]

1. Man bruger formlen for vinklen mellem to vektorer og solve() kommandoen:

   solve(cos(x*1.°)=dotP(a,b)/(norm(a)*norm(b)),x)|0<x<180 ▸ x=40.236

   Vinklen mellem vektor a og vektor b er 40,2°

2. Man bruger formlen for projektionen af en vektor på en anden: a_b = b·(a·b)/|b|²

   b*1.*dotP(a,b)/(norm(b))² ▸ (0.897,2.24)

   Dvs. a_b = (0,897;2,24)

Svar på opgave 8:

Løst i Ti-Nspire.

1. Man opretter to liter med data for henholdsvis højder og diameter:

   hoejde:={0.5,1.,1.5,2.,2.5,3.,3.5} ▸ {0.5,1.,1.5,2.,2.5,3.,3.5}

   diameter:={20.5,21.,21.4,22.,22.3,23.,23.5} ▸ {20.5,21.,21.4,22.,22.3,23.,23.5}

   Man bruger kommandoen:

   ExpReg hoejde,diameter,1: CopyVar stat.RegEqn,f1: stat.results ▸

   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",20.0385]
   ["b",1.04624]
   ["r²",0.995882]
   ["r",0.997939]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Her aflæses a til 1.046 og b til 20,04

   Bemærk at Ti-Nspire bruger a og b i modsat betydning af opgaven.

2. Man skal beregne d(6) = 20,04·1.046⁶ = 26.28, dvs. diameteren er 26.28 m

3. Tallet a er fremskrivningsfaktoren, dvs. det tal som man skal gange diameteren med hver gang højden stiger en km.

   Forøgelsen af højden kaldes x. Man skal løse ligningen: d(h+x) = 1,5·d(h):

   d(h):=20.0385*(1.04624)^h ▸ Udført

   solve(d(h+x)=1.5*d(h),x) ▸ x=8.97

   Dvs. højden skal forøges med 8,97 km før diameteren bliver 50 % større

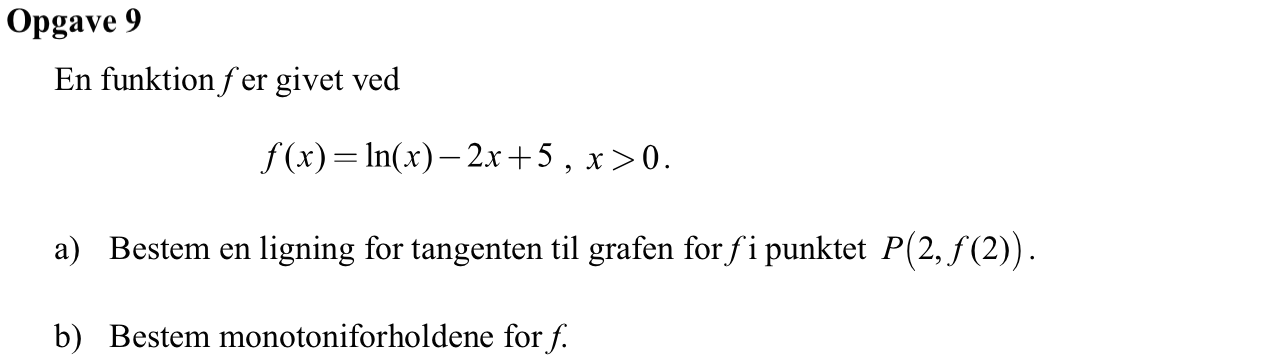
Svar på opgave 9:

Løsning i Ti-Nspire.

1. Funktionen f(x) defineres:

   f(x):=ln(x)-2*x+5 ▸ Udført

   Man bruger tangentLine():

   y=tangentLine(f(x),x,2.) ▸ y=4.6931-1.5*x

   Dvs tangenten gennem P er: y = -1.5x + 4.69

2. Man finder de x > 0, hvor f´(x) < 0:

   solve(derivative(f(x),x)<0.,x)|x>0 ▸ x>0.5

   Man finder de x hvor f´(x) > 0:

   solve(derivative(f(x),x)>0.,x)|x>0 ▸ 0.<x<0.5

   Man får monotoniforholdene:

   f(x) vokser for 0 < x < 0,5

   f(x) aftager for x > 0,5

Svar på opgave 10:

1. Radius for kuglen er lig med længden af vektoren CP = (1,0,5) - (1,2,-1) = (0,-2,6)

   Længden af CP er sqrt(0² + (-2)² + 6²) = √40

   Kuglens ligning bliver: (x - 1)² + (y - 2)² + (z + 1)² = 40

2. Α er tangentplan til kuglen, hvis afstanden mellem α og kuglens centrum er lig med kuglens radius. Man bruger afstandsformlen for et punkt og et plan:

   abs(0*1+1*2+6*(−1)+(−40.))/sqrt(0²+1²+6²) ▸ 7.2336

   Denne afstand er større end radius, som er kvadratrod 40 = 6.32. Dermed er α ikke tangentplan til kuglen.

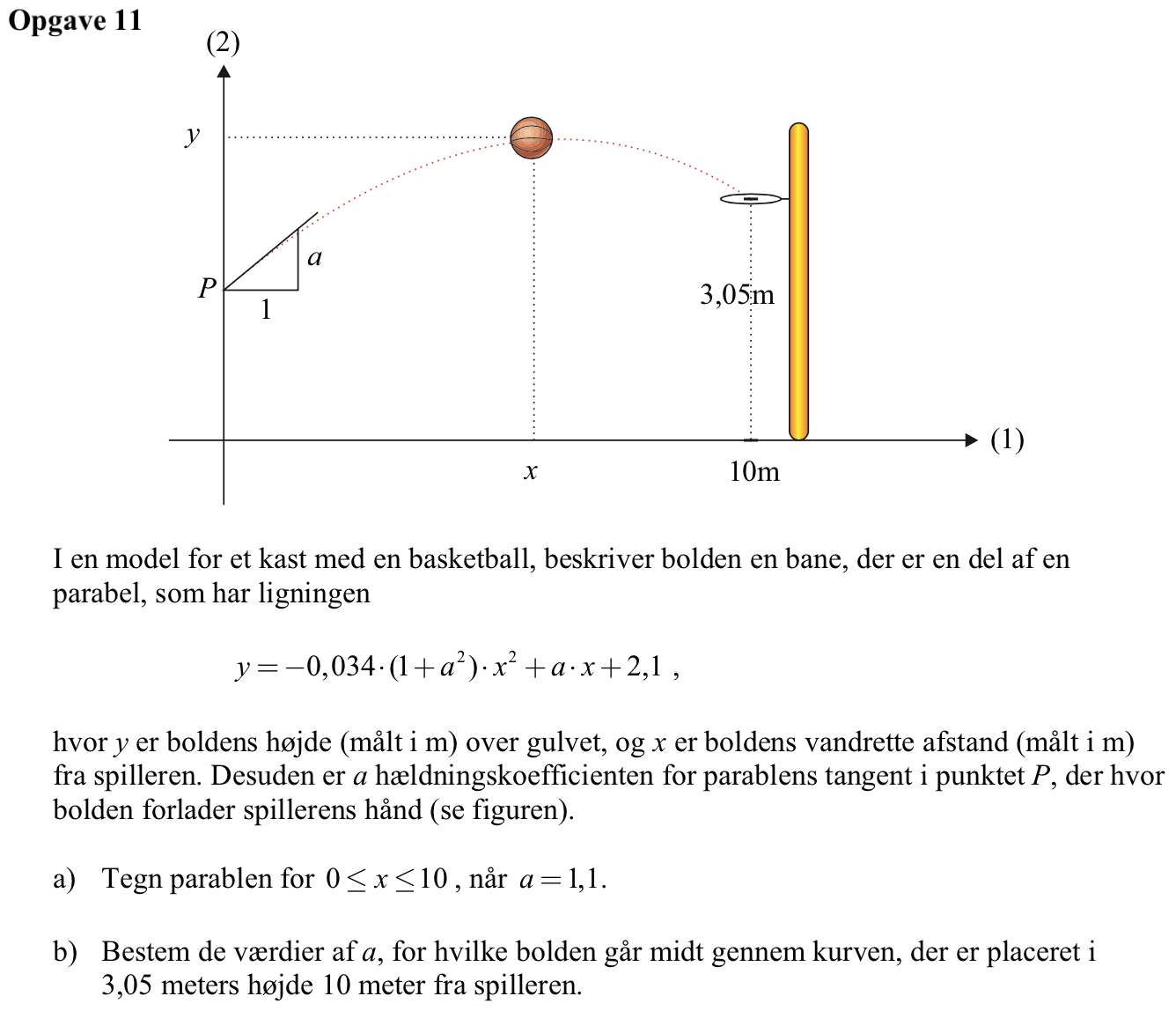
Svar på opgave 11:

1. Tegnet i Geogebra:

   

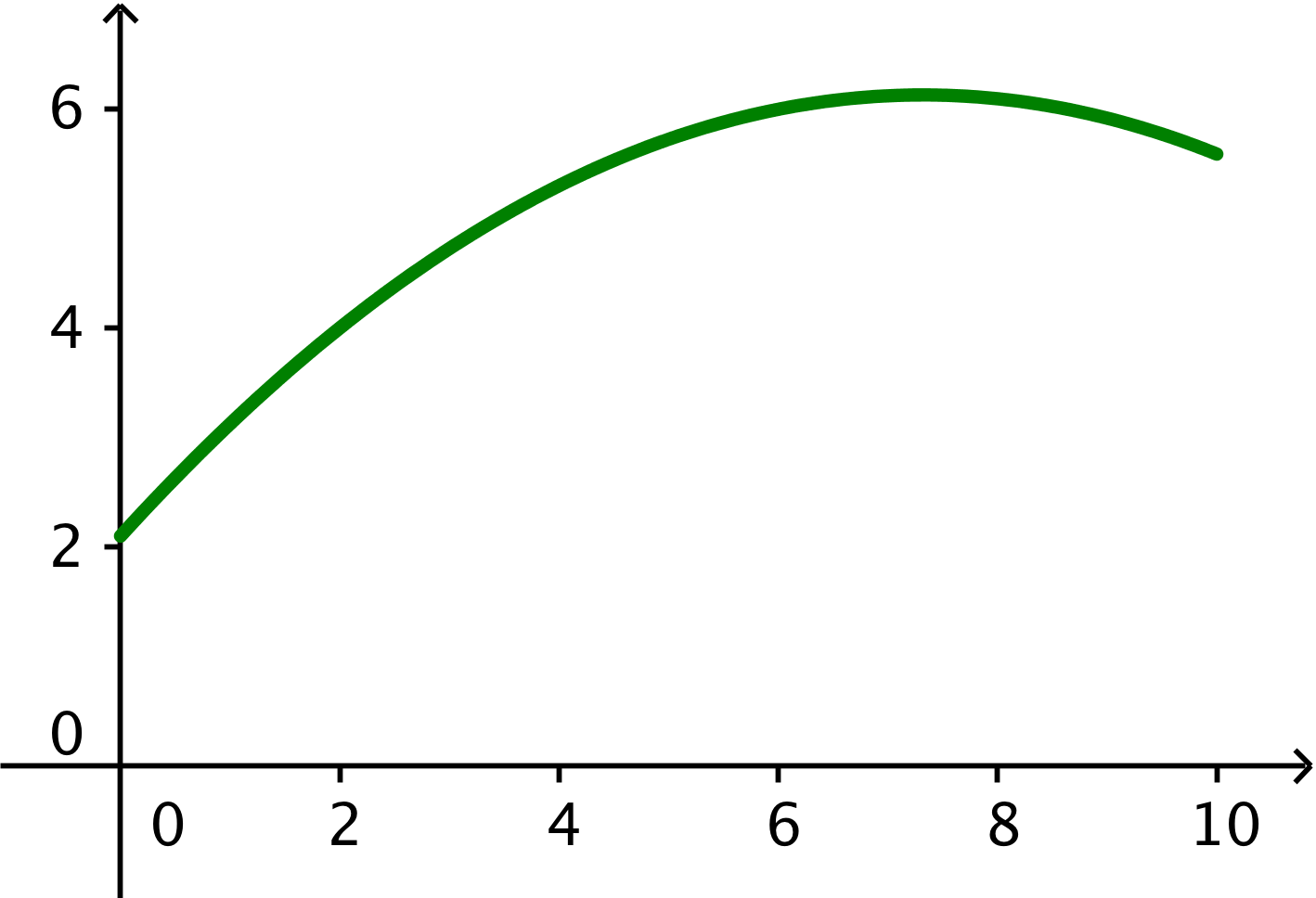
2. Man skal finde de a, hvor x = 10 og y = 3,5. Løst i Ti-Nspire:

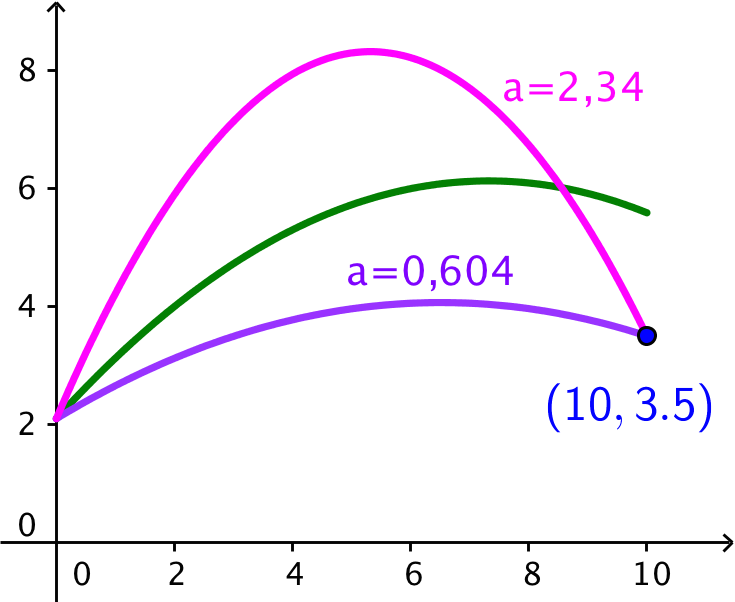
   solve(y=−0.034*(1+a²)*x²+a*x+2.1,a)|x=10 and y=3.5 ▸ a=0.60406 or a=2.3371

   Dvs. a = 0,604 eller a = 2,34

   Kontroltegning i Geogebra:

   

Svar på opgave 12:

Løsning i Ti-Nspire:

1. Nulhypotese: afvigelsen mellem observerede og forventede hyppigheder skyldes tilfældigheder.

2. Man opretter to lister med henholdsvis observationer og forventede hyppigheder:

   observeret:={172,168,150,188,185,137} ▸ {172,168,150,188,185,137}

   forventet:=sum(observeret)*{(1./6),(1./6),(1./6),(1./6),(1./6),(1./6)} ▸ {166.67,166.67,166.67,166.67,166.67,166.67}

   Kommandoen χ²GOF observeret,forventet,5: stat.results, hvor 5-tallet er antal frihedsgrader, giver resultatet:

   [["Titel","χ²-Goodness of Fit test"]
    ["χ²",11.876]
    ["PVal",0.0365]
    ["df",5.]
    ["CompList","{...}"]]

   Man aflæser PVal = 0,0365 = 3,7 %. Da dette er mindre en 5 % forkastes nulhypotesen.

Svar på opgave 13:

Løsning i Ti-Nspire.

1. Man definerer f(x):

   f(x):=−0.00105*x³+0.0467*x²-0.452*x+4.78 ▸ Udført

   Arealet af M er integralet fra x = 0 til x = 20.

   integral(f(x),x,0,20) ▸ 87.733

   Dvs. arealet af M er 87,73

2. Rumfanget er

   π*integral((f(x))²,x,0,20) ▸ 1246.2

   Dvs. rumfanget af vasen er 1246

Svar på opgave 14:

1. Løst i Ti-Nspire. Man bruger oplysningen fra skemaet: N(0) = 3:

   deSolve(n'=a*n*(90-n) and n(0)=3,t,n) ▸ n=90*exp(90*a*t)/(exp(90*a*t)+29)

   Her skal man bruge den anden oplysning: N(11) = 43 til at finde a:

   solve(90*exp(90*a*t)/(exp(90*a*t)+29)=43.,a)|t=11 ▸ a=0.00331

   Dvs. N(t) = 90*1,347^t/(1,347^t+29) = 90/(1 + 29*1,347^-t)

2. Den øvre grænse for antallet af ulvepar er antallet af uvepar for tiden gående mod uendelig. Af udtrykket 90/(1 + 29*1,347^-t) ses, at når t går mod uendelig, går 1,347^-t mod nul og dermed går nævneren mod 1.

   Dermed går N(t) mod 90 ulvepar for tiden gående mod uendelig.

   Man skal finde maksimum for N'(t) og bruger fMax():

   fMax(derivative(N(t),t),t) ▸ t=11.298

   Dvs. største væksthastighed optræder efter 11,3 år

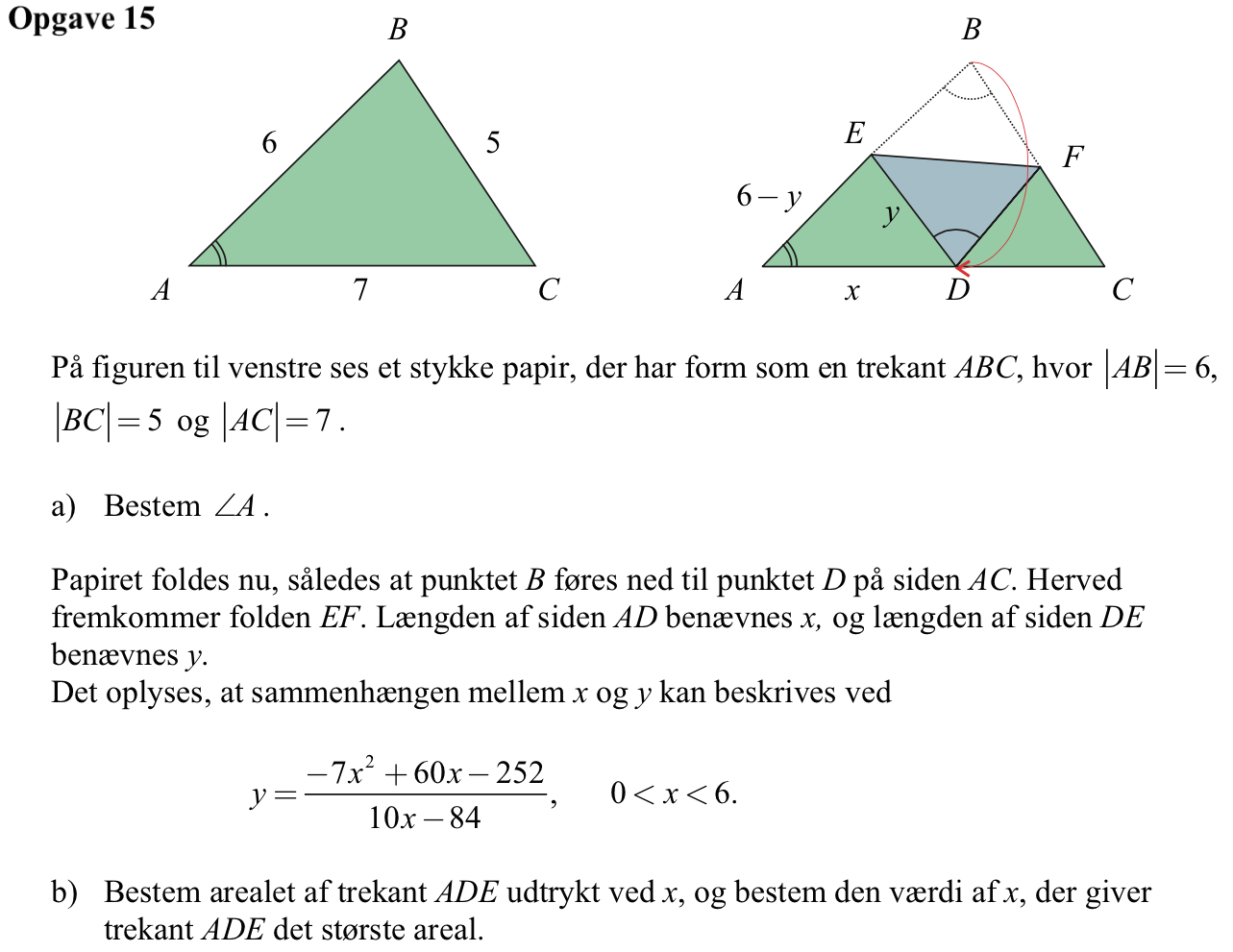
Svar på opgave 15:

Løsning i Ti-Nspire.

1. Vinkel A findes ved hjælp af en cosinusrelation:

   

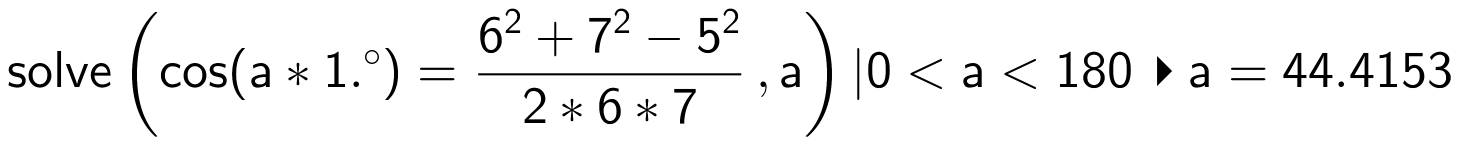
   Dvs. vinkel A = 44.4°

2. Trekantens areal er 0,5·grundlinje·højde. Grundlinje = x og højde = (6 - y)·sin(∠A). Man bruger fMax() på udtrykket for arealet med de givne betingelser:

   

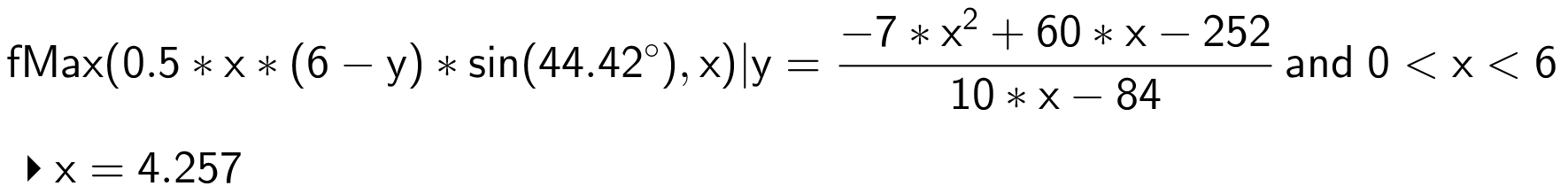
   Det ses, at det x, som giver det maksimale areal, er 4,26