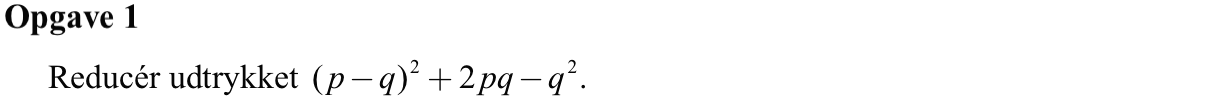
Svar på opgave 1:

1. (p - q)² + 2pq - q² =

   p² - 2pq + q² + 2pq - q² =

   p²

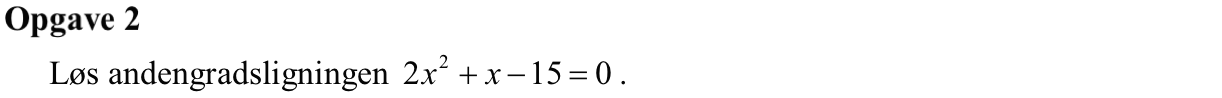
Svar på opgave 2:

1. 2x² - x - 15 = 0 ⇔

   x = -0,25 ± 0,25·√[1 + 4·2·15] ⇔

   x = -0,25 ± 0,25·11 ⇔

   x = -3 ∨ x = 2

Svar på opgave 3:

1. 1,5 er startværdien for koncentrationen, mens 0,64 er fremskrivningsfaktoren som koncentrationen ganges med hver time.

Svar på opgave 4:

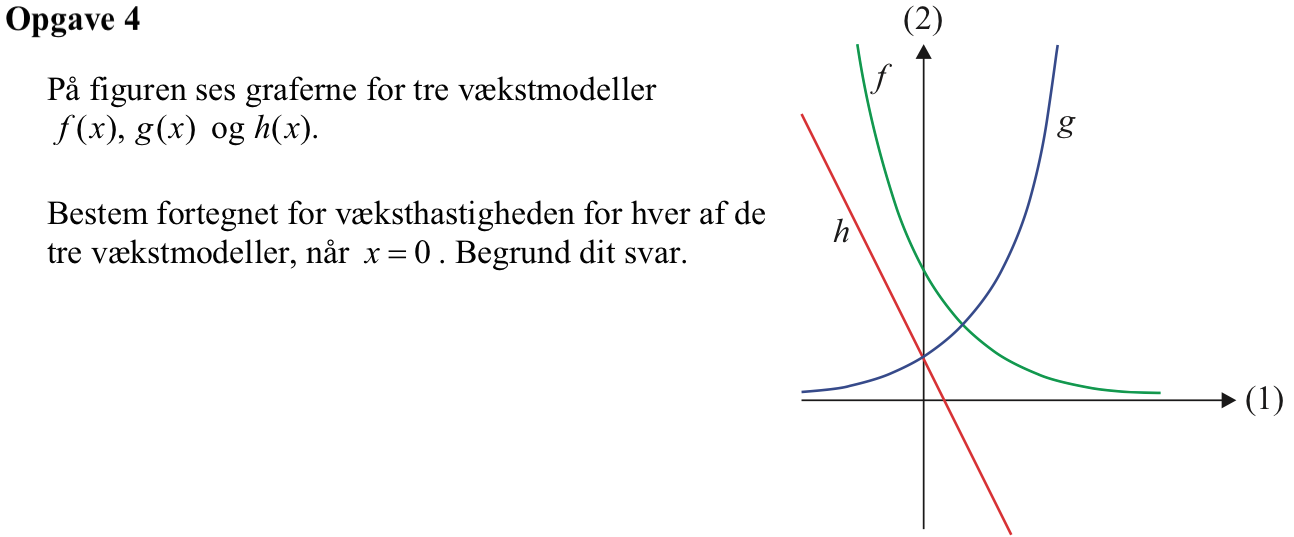
1. Man aflæser følgende af hældningen af kurverne i deres skæringspunkt med y-aksen:

   f: fortegn er negativt

   g: fortegn er positivt

   h: fortegn er negativt

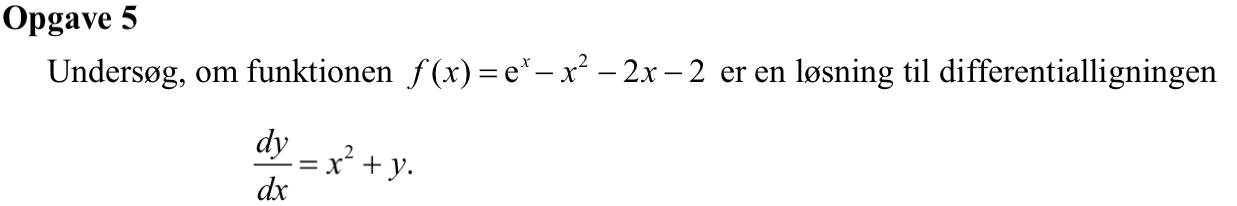
Svar på opgave 5:

1. Man skal gøre prøve og se om man får det samme på begge sider af differentialligningen.

   Venstre side: dy/dx = f´(x) = e^x - 2x - 2

   Højre side: x² + y = x² + f(x) = x² + e^x - x² - 2x -2 = f(x) + e^x = e^x - 2x - 2

   Dvs. prøven stemmer og f(x) er en løsning til differentialligningen.

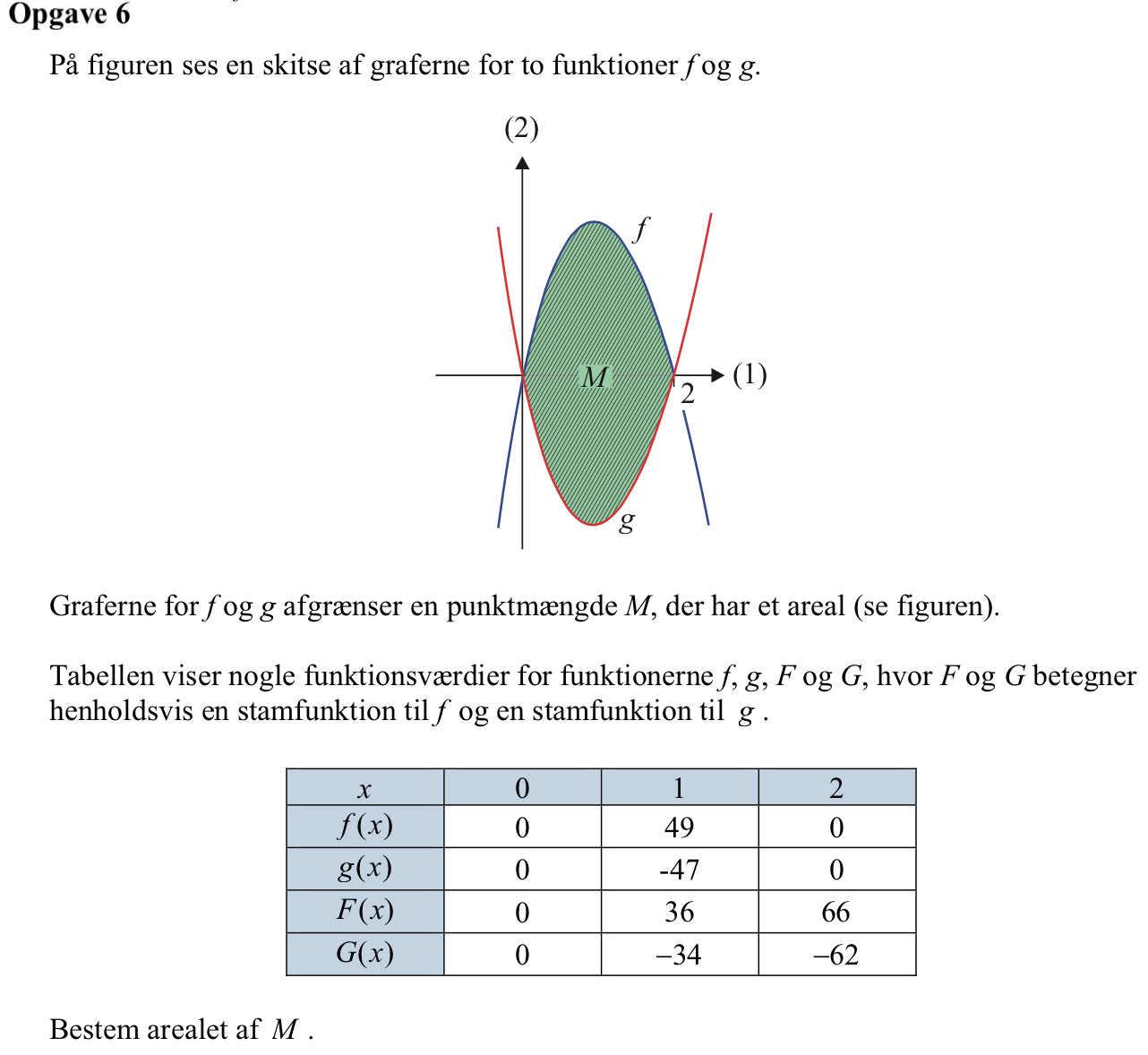
Svar på opgave 6:

1. Arealet af M er [F(2) - G(2)] - [F(0) - G(0)] = 66 - (-62) - 0 - 0 = 128

Svar på opgave 7:

Løsning i Ti-Nspire.

Vektorerne oprettes:

a:=[7,3] ▸ [7,3]

b:=[t,6] ▸ [t,6]

1. Man bruger formlen for vinklen mellem to vektorer og solve() kommandoen:

   solve(cos(x*1.°)=dotP(a,b)/(norm(a)*norm(b)),x)|0<x<180 and t=2 ▸ x=48.36

   Vinklen mellem vektor a og vektor b er 48,4°

2. Man opretter en 2×2 matrix, hvor første søjle er vektor a og anden søjle er b. På den bruger man det() kommandoen og solve():

   

   Dvs. den værdi af t, som giver determinanten 30 er t = 4

Svar på opgave 8:

Løst i Ti-Nspire.

1. Man opretter to lister med data for henholdsvis højder og belastningsevner:

   hoejde:={359,395,432,478,524,572,620,716} ▸ {359,395,432,478,524,572,620,716}

   belastning:={3800,4300,4820,5500,6180,6920,7660,9200} ▸ {3800,4300,4820,5500,6180,6920,7660,9200}

   Man bruger kommandoen for potensregression på de to lister:

   PowerReg hoejde,belastning,1: CopyVar stat.RegEqn,f1: stat.results ▸

   [["Titel","Potensregression"]
   ["RegEqn","a*x^b"]
   ["a",2.02499]
   ["b",1.28131]
   ["r²",0.999985]
   ["r",0.999993]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Her aflæses a til 1,281 og b til 2,025

   Bemærk at Ti-Nspire bruger a og b i modsat betydning af opgaven.

2. Man skal beregne f(668) = 2,025·668^1,28131 = 8430,187, dvs. belastningsevnen er 8430·10³ mm³

3. Man bruger formlen for procent-procentvækst for potensfunktioner:

   (1,15^1,281 - 1)·100 % = 19.61 %, dvs. belastningsevnen vokser med 19,6 % når højden vokser med 15 %.

Svar på opgave 9:

Løsning i Ti-Nspire.

1. Funktionen f(x) defineres:

   f(x):=ln(x^(2)+5)+0.5*x+1 ▸ Udført

   Man finder skæringspunktet med x-aksen:

   solve(f(x)=0,x) ▸ x=−12.0116

   Dvs skæringspunktet med førsteaksen har koordinaterne: (−12,01;0)

2. Arealet er lig med integralet af f(x) fra x = -12,01 til x = 0:

   integral(f(x),x,−12.0116,0) ▸ 18.248

   M har arealet 18,248

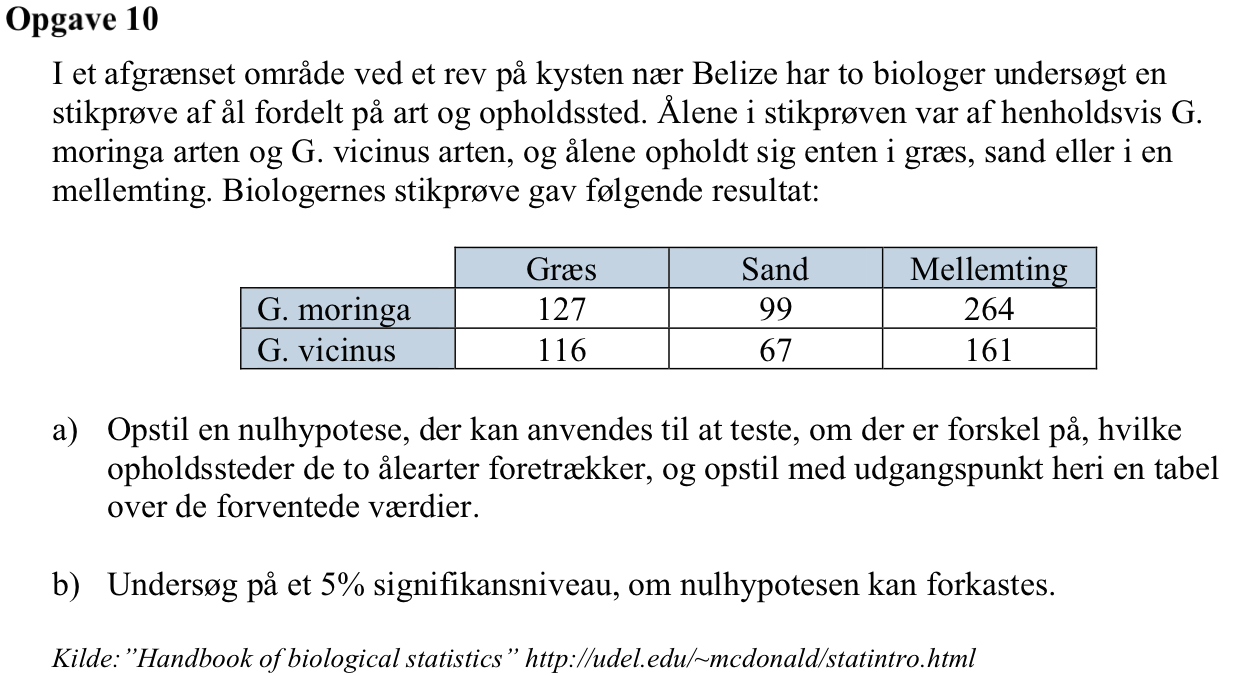
Svar på opgave 10:

Løsning i Ti-Nspire:

1. Nulhypotesen er, at valg af opholdssted er uafhængig af fiskeart.

2. Man opretter en matrix med observerede data:

   

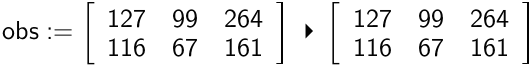
   Man bruger kommandoen for en chi-i-anden uafhængighedstest på matricen af observationer:

   χ²2way obs: stat.results ▸

   [["Titel","χ²-uafhængighedstest"]
   ["χ²",6.2621260618814]
   ["PVal",0.043671348574177]
   ["df",2.]
   ["ExpMatrix","[...]"]
   ["CompMatrix","[...]"]]

   Af testen fremgår, at PVal = 0,044 = 4,4 %. Da dette er mindre end 5 % forkastes nulhypotesen

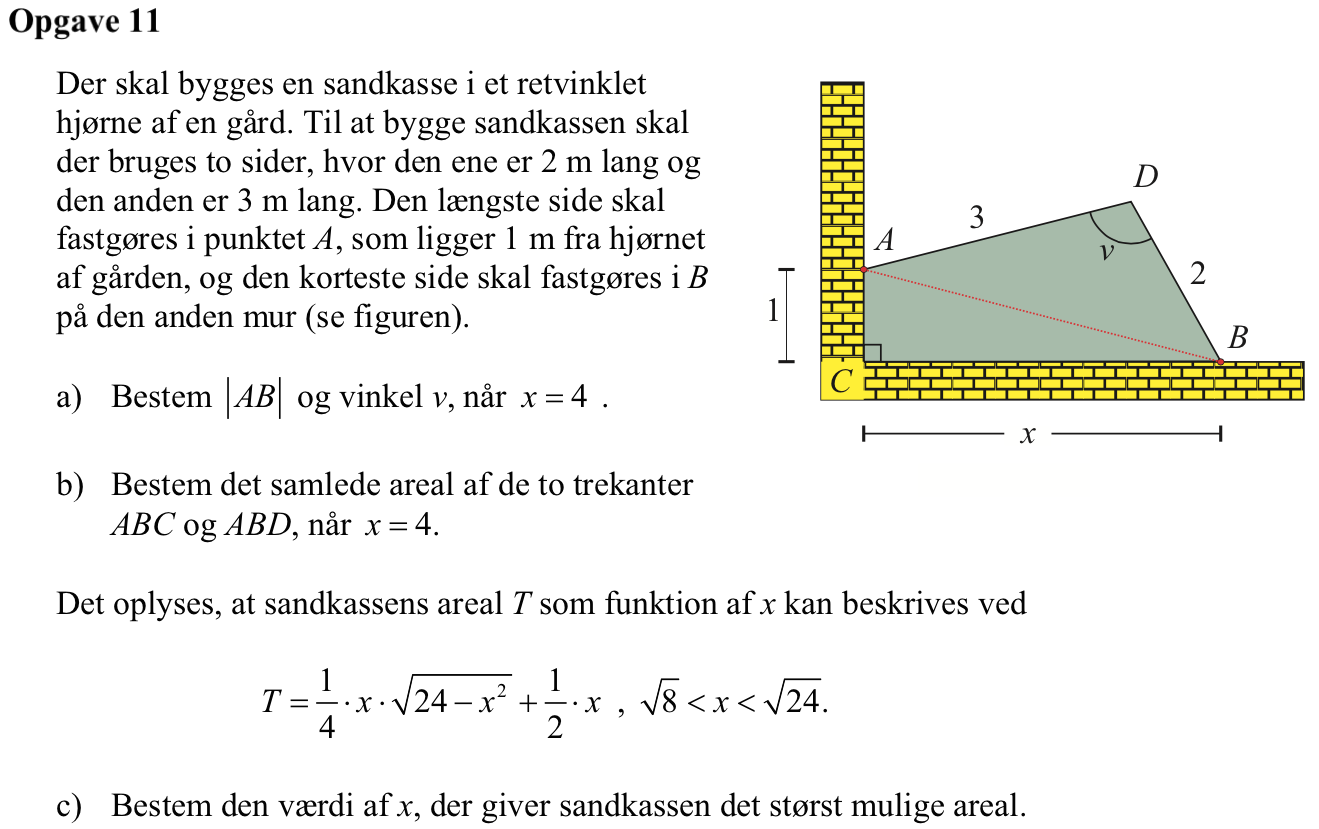
Svar på opgave 11:

1. |AB| findes ved hjælp af Pythagoras læresætning:

   1² + 4² = |AB|² ⇒ |AB| = √17 = 4,123

   Man bruger en cosinusrealtion:

   solve(cos(v*1.°)=(3²+2²-17)/(2*3*2),v)|0<v<180 ▸ v=109.471

   Vinklen v = 109,5°

   Arealet af trekant ABC er 0,5·1·4 = 2

   For st finde arealet af trekant ADB finder man først vinklen BAD ved hjælp af en sinusrelation:

   solve(sin(x*1.°)/2=sin(109.471*1.°)/sqrt(17),x)|0<x<90 ▸ x=27.21

   Dvs. vinkel BAD er 27,21°. Arealet af trekant ADB = 0,5·3·sin(27,21°) = 2,828

   Dermed bliver det samlede areal af de to trekanter 2 + 2,828 = 4,828

2. Det x der giver det maksimale areal findes ved kommandoen fMax():

   t(x):=(1/4)*x*sqrt(24-x²)+(1/2)*x

   fMax(t(x*1.),x)|sqrt(8)<x<sqrt(24) ▸ x=3.87298

   Dvs. det x, som giver det største areal for sandkassen er 3,873

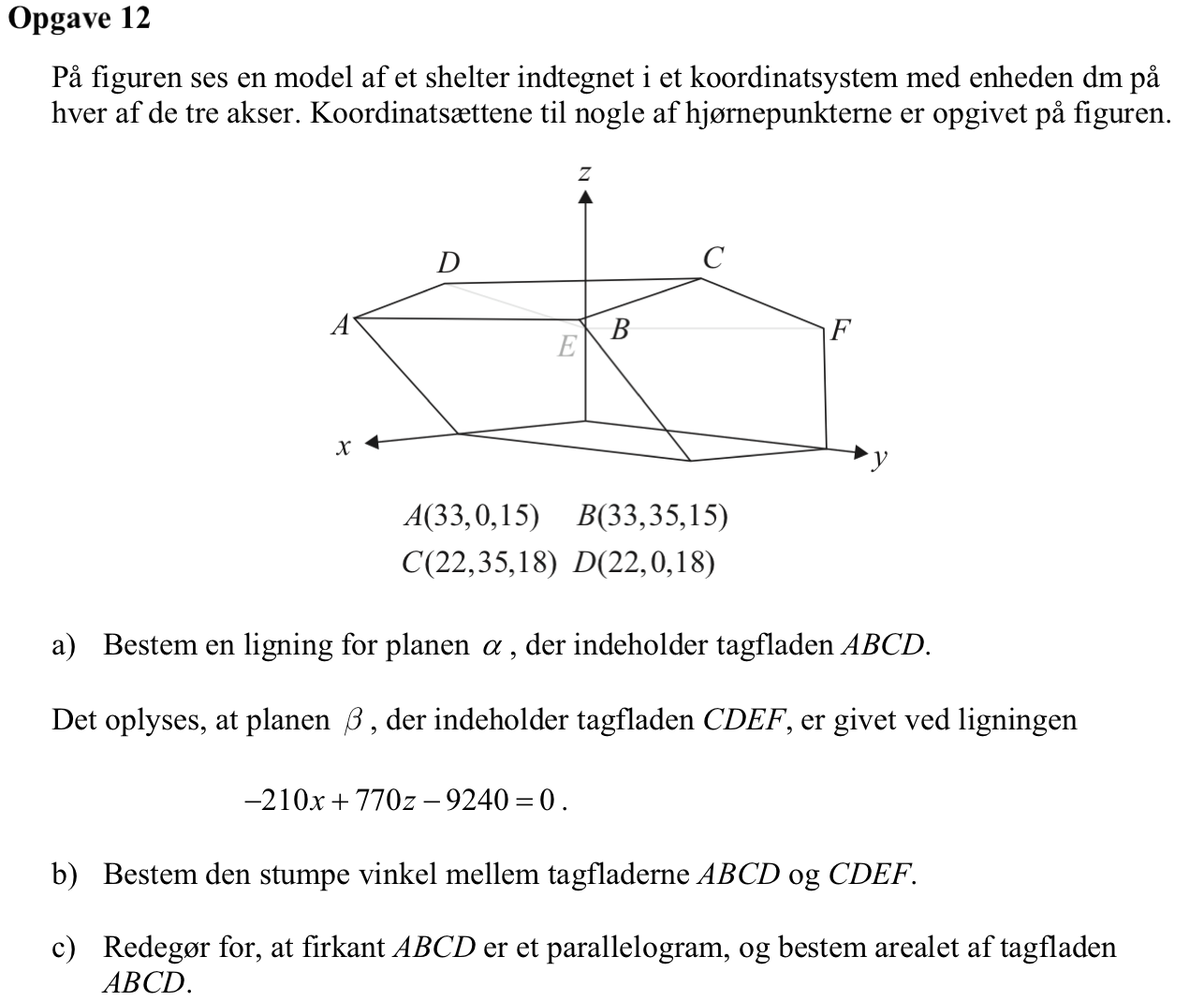
Svar på opgave 12:

Løsning i Ti-Nspire:

1. Man opretter punkterne A-D og vektorerne AB og AC:

   a:=[33,0,15] ▸ [33,0,15]

   b:=[33,35,15] ▸ [33,35,15]

   c:=[22,35,18] ▸ [22,35,18]

   d:=[22,0,18] ▸ [22,0,18]

   ab:=b-a ▸ [0,35,0]

   ac:=c-a ▸ [−11,35,3]

   Man finder en normalvektor n til planen ved at tage krydsproduktet AB×AC (dette divideres derefter med største fælles divisor (greatest common divisor) for at få små hele tal):

   abxac:=crossP(ab,ac) ▸ [105,0,385]

   n:=abxac/gcd(105,385) ▸ [3,0,11]

   Planens ligning findes:

   dotP(n,[x,y,z]-a)=0 ▸ 3*x+11*z-264=0

   Dvs. planens ligning er 3x + 11z - 264 = 0

2. Planens β's ligning kan skrives: -210x + 0y + 770z - 9240 = 0. Dens normalvektor m aflæses til (-210,0,770). Dette divideres igennem med 70 for at få små hele tal: m = (-3,0,11).

   Den stumpe vinkel mellem α og β beregnes:

   solve(cos(x*1.°)=−abs(dotP(n,m))/(norm(n)*norm(m)),x)|0<x<180 ▸ x=149.49

   Dvs. den stumpe vinkel er 149,5°

3. ABCD er et parallelogram, fordi AD + AB = AC. Bevis:

   ad:=d-a ▸ [−11,0,3]

   ad+ab ▸ [−11,35,3]

   ac = [−11,35,3], dermed er AD + AB = AC.

   Arealet af ABCD er længden af ab×ac = norm(abxac)*1. ▸ 399.061 = 399,1

Svar på opgave 13:

Løsning i Ti-Nspire.

1. Man definerer f(x):

   f(x):=3*sin(2*x+0.7)+1 ▸ Udført

   Man bruger kommandoen tangentLine()

   y=tangentLine(f(x),x,3) ▸ y=5.486*x-14.24

   Dvs. tangentlinjen gennem (3,f(3)) er y = 5,486x - 14,24

2. Mindsteværdien for sinusfunktionen er -1 og størsteværdien er 1. Det giver for f(x):

   Mindsteværdi: 3·(-1) + 1 = -2, størsteværdi: 3·1 + 1 = 4

   Perioden for sin(v) er 2π. Her er v = 2·x + 0,7, dvs. perioden bliver det p for hvilke 2·(x+p) + 0,7 øges med 2π.

   Man får: 2·(x+p) + 0,7 = 2x + 0,7 + 2π ⇒ 2p = 2π ⇒ p = π

   Dvs. perioden for f(x) er π

Svar på opgave 14:

Løst i Ti-Nspire.

1. Man bruger desolve kommandoen:

   deSolve(y'=a*(20+5*t-y) and y(0)=20,t,y) ▸ y=5*((a*t+4*a-1)*exp(a*t)+1)*exp(−a*t)/a

   Løsningen f(t) defineres ud fra dette:

   f(t):=5*((a*t+4*a-1)*exp(a*t)+1)*exp(−a*t)/a

   Man finder temperaturen efter 16 minutter, når a=0,07:

   f(16)|a=0.07 ▸ 51.877

   Dvs. temperaturen efter 16 minutter er 51,9°C

2. Man løser ligningen f(16) = 50 med hensyn til a:

   solve(f(16)=50,a) ▸ a=−1.175494E−38 or a=1.175494E−38 or a=0.06419

   Løsningerne: a=±1.175494E−38 er ugyldige, da de svarer til det mindste tal, som kan repræsenteres i Ti-Nspire. Når man når grænsen for Ti-Nspire's præcision opstår let afrundingsfejl.

   Den gyldige løsning er a = 0,064