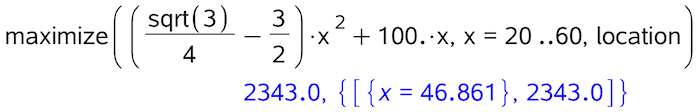Svar på opgave 1:

1. Parablens toppunkt har formlen: (-b/(2·a),c - b²/(4·a)) =

   (-4/(2·2),-6 - 2²/(4·2)) =

   (-1,-8)

Svar på opgave 2:

1. Trekant ABC og trekant ADE er ensvinklede, fordi de har vinkel A til fælles, og fordi de to modstående sider til vinkel A er parallelle.

   Skaleringsfaktoeren er |AE|/|AC| = 10/4 = 5/2

   |DE| = |BC|·5/2 = 2·5/2 = 5

Svar på opgave 3:

1. x + y = 11 ∧ 6x + 2y = 42 ⇔

   x = 11 - y ∧ 3x + y = 21 ⇔

   x = 11 - y ∧ 3·(11 - y) + y = 21 ⇔

   x = 11 - y ∧ 33 - 3y + y = 21 ⇔

   x = 11 - y ∧ -3y + y = 21 - 33 ⇔

   x = 11 - y ∧ -2y = -12 ⇔

   x = 11 - 6 ∧ y = 6 ⇔

   x = 5 ∧ y = 6

Svar på opgave 4:

1. Man omskriver cirklens ligning til standardform ved hjælp af kvadratkomplettering:

   x² - 6x + y² + 2y - 26 = 0 ⇔

   (x - 3)² - 9 + (y + 1)² -1 - 26 = 0 ⇔

   (x - 3)² (y + 1)² = 36 = 6²

   Heraf ses at centrum er: (3,-1) og radius er 6

Svar på opgave 5:

1. Man får: f´(x) = 3·a·x² + 10x + 2.

   f´(1) = 3·a·1² + 10·1 + 2 = 3·a + 10 + 2 = 3·a + 12.

   f´(1) = -3 ⇒ 3·a + 12 = -3 ⇔ a = -5

Svar på opgave 6:

1. Man bruger substitutionen: y = x² + 7, dy = 2xdx, der giver:

   

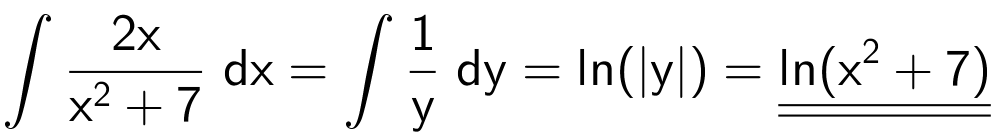
   Numerisktegnene kan udelades til sidst, da x² + 7 altid er større end 0.

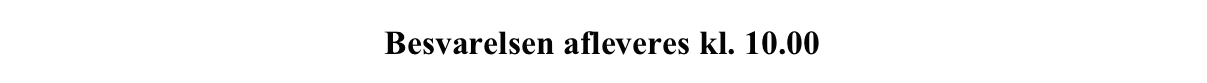
Svar på opgave 7:

Løsning i Ti-Nspire.

1. Man bruger en sinusrealtion til at finde ∠B. Man sætter x = ∠B og bemærker, at ∠B <100°, da ∠B + ∠C = 180° - 80° = 100°. Man får:

   

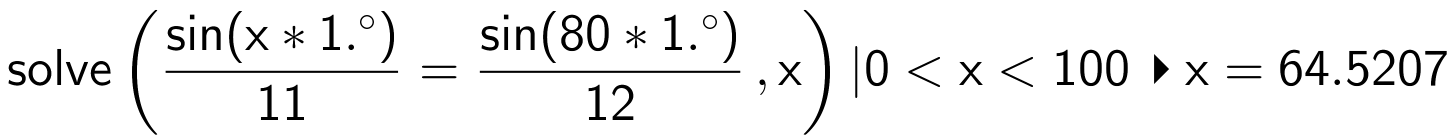
   Dvs. ∠B = 64,5°

   ∠C = 180° - ∠A - ∠B = 180° - 80° - 64,5° = 35,48° = 35,5°

2. Tegningen nedenfor, som er lavet i Geogebra, viser trekanten med medianen m_a. Man kalder fodpunktet for medianen for D.

   

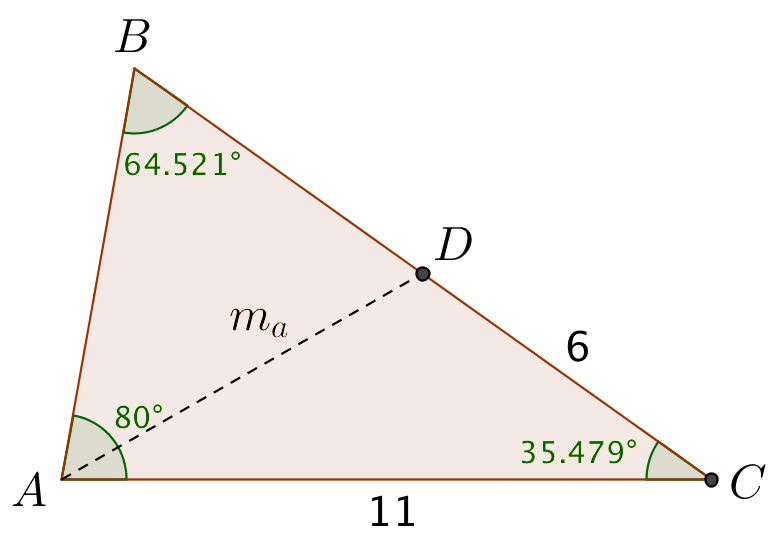
   Man anvender en cosinusrelation på trekanten ACD, idet længden af m_a kaldes x, og idet det kræves at x > 0:

   

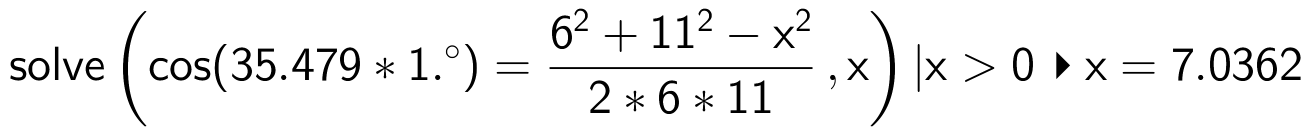
   Man får at m_a = 7,036

Svar på opgave 8:

Løst i Ti-Nspire.

1. Man opretter to lister med data for henholdsvis højder og belastningsevner:

   aar:={0,5,10,15,20,25,30,35,40,45} ▸ {0,5,10,15,20,25,30,35,40,45}

   moeder:={359,539,811,1195,1717,2452,3372,5107,8164,10969} ▸ {359,539,811,1195,1717,2452,3372,5107,8164,10969}

   Man bruger kommandoen for potensregression på de to lister:

   ExpReg aar,moeder,1: CopyVar stat.RegEqn,f1: stat.results ▸

   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",370.3758045107]
   ["b",1.0786603416125]
   ["r²",0.99894670557677]
   ["r",0.99947321403666]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Her aflæses a til 1,0787 og b til 370,38

   Bemærk at Ti-Nspire bruger a og b i modsat betydning af opgaven.

2. År 2010 svarer til t = 2010 - 1963 = 47.

   Man skal finde M(47) = 370,38·1,0787⁴⁷ = 13008

   Fordoblingskonstanten er ln(2)/ln(1,0787) år = 9,15 år

3. M'(37) findes ved kommandoen:

   derivative(370.376*(1.07866)^t,t)|t=37 ▸ 461.9

   Dvs. M'(37) = 461,9 møder/år, dvs. antal møder pr. år steg med 462 i år 2000.

Svar på opgave 9:

Løsning i Geogebra og Ti-Nspire.

1. Nedenfor er grafen skitseret i Geogebra.

   

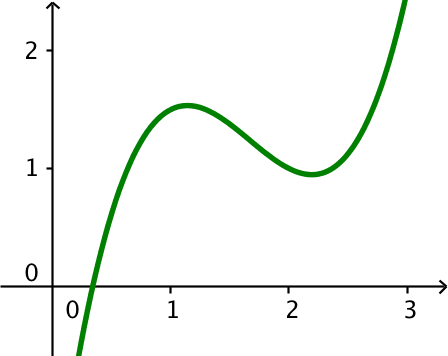
   Man finder ligningen for tagenten i Ti-Nspire:

   y=tangentLine(x³-5*x²+7.5*x-2,x,1) ▸ y=0.5*x+1.

   Dvs. tangenten har ligningen y = 0,5·x + 1

2. M tegnet i Geogebra:

   

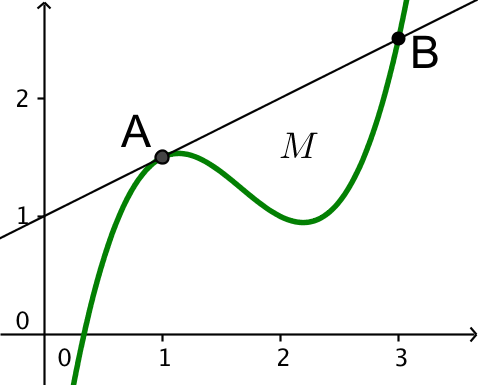
   Førstekoordinaten til B findes i Ti-Nspire:

   solve(x³-5*x²+7.5*x-2=0.5*x+1.,x)|x≠1 ▸ 3 (A har første koordinaten x=1)

   Dvs. førstekoordinaten for B er x = 3

   M's areal findes med kommandoen:

   integral(abs(x³-5*x²+7.5*x-2-(0.5*x+1.)),x,1,3) ▸ 1.333 (integralet af den numeriske værdi af y-værdien af tangenten og f(x) fra x=1 til x=3)

   Dvs. arealet af M er 1,333

Svar på opgave 10:

Løsning i Ti-Nspire.

1. Linjen går igennem A og har vektoren AB som retningsvektor.

   AB = (9,17) - (1,5) = (8,12)

   Parameterfremstillingen for l bliver: (1,5) + t·(8,12), t ∈R

2. P's projektion på l findes som OA + AP's projektion på AB:

   a:=[1,5] ▸ [1,5]

   b:=[9,17] ▸ [9,17]

   p:=[−10,21] ▸ [−10,21]

   ab:=b-a ▸ [8,12]

   ap:=p-a ▸ [−11,16]

   ap_ab:=(dotP(ab,ap)/norm(ab)²)*ab ▸ [4,6] (vektor AP's projektion på vektor AB)

   a+ap_ab ▸ [5,11]

   Dvs. P's projektion på l er (5,11)

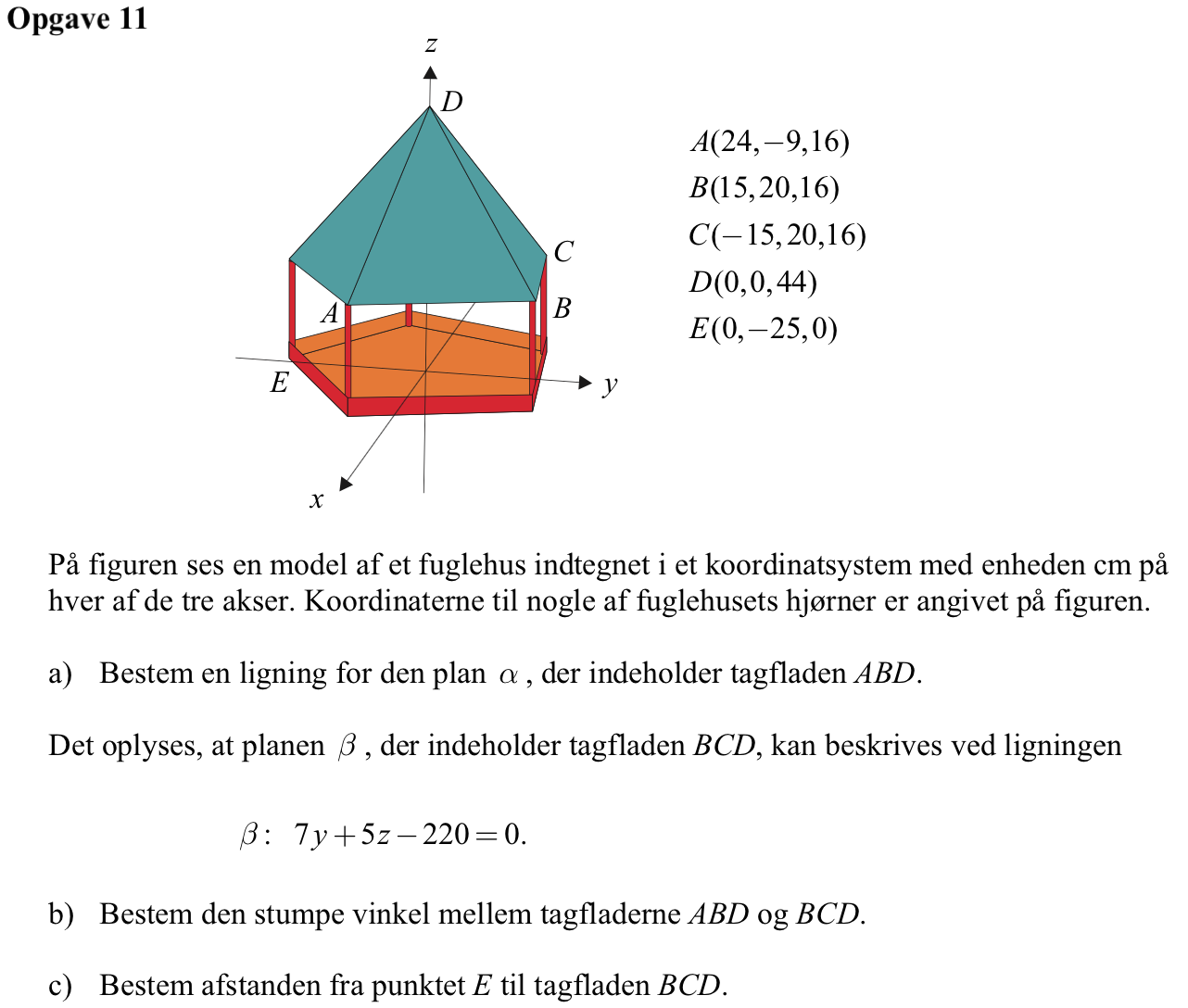
Svar på opgave 11:

Løsning i Ti-Nspire.

1. a:=[24,−9,16] ▸ [24,−9,16]

   b:=[15,20,16] ▸ [15,20,16]

   c:=[−15,20,16] ▸ [−15,20,16]

   d:=[0,0,44] ▸ [0,0,44]

   e:=[0,−25,0] ▸ [0,−25,0]

   ab:=b-a ▸ [−9,29,0]

   ad:=d-a ▸ [−24,9,28]

   n:=crossP(ab,ad) ▸ [812,252,615]

   dotP(n,[x,y,z]-a)=0 ▸ 812*x+252*y+615*z-27060=0

   Planens ligning er α: 812x + 252y + 615z - 27060 = 0

2. Den stumpe vinkel mellem α og β findes som den stumpe vinkel mellem deres normalvektorer n og m.

   Planen βs normalvektor m aflæses af ligningen: 0x + 7y + 5z - 220 = 0 og oprettes i Ti-Nspire:

   n:=[0,7,5] [0,7,5]

   Den stumpe vinkel mellem n og m findes ved kommandoen:

   solve(cos(x*1.°)=−abs(dotP(n,m))/(norm(n)*norm(m)),x)|0<x<180 ▸ x=122.42

   Dvs. den stumpe vinkel mellem α og β er 122,4°

3. Man bruger afstandsformlen mellem punkt og plan. Her får man i Ti-Nspire:

   Formlen giver her:

   abs(0*0+(−25)*7+0*5-220)/sqrt(0²+7²+5²)*1. ▸ 45.918

   Dvs. afstanden mellem punktet E og tagfladen BCD er 45,92

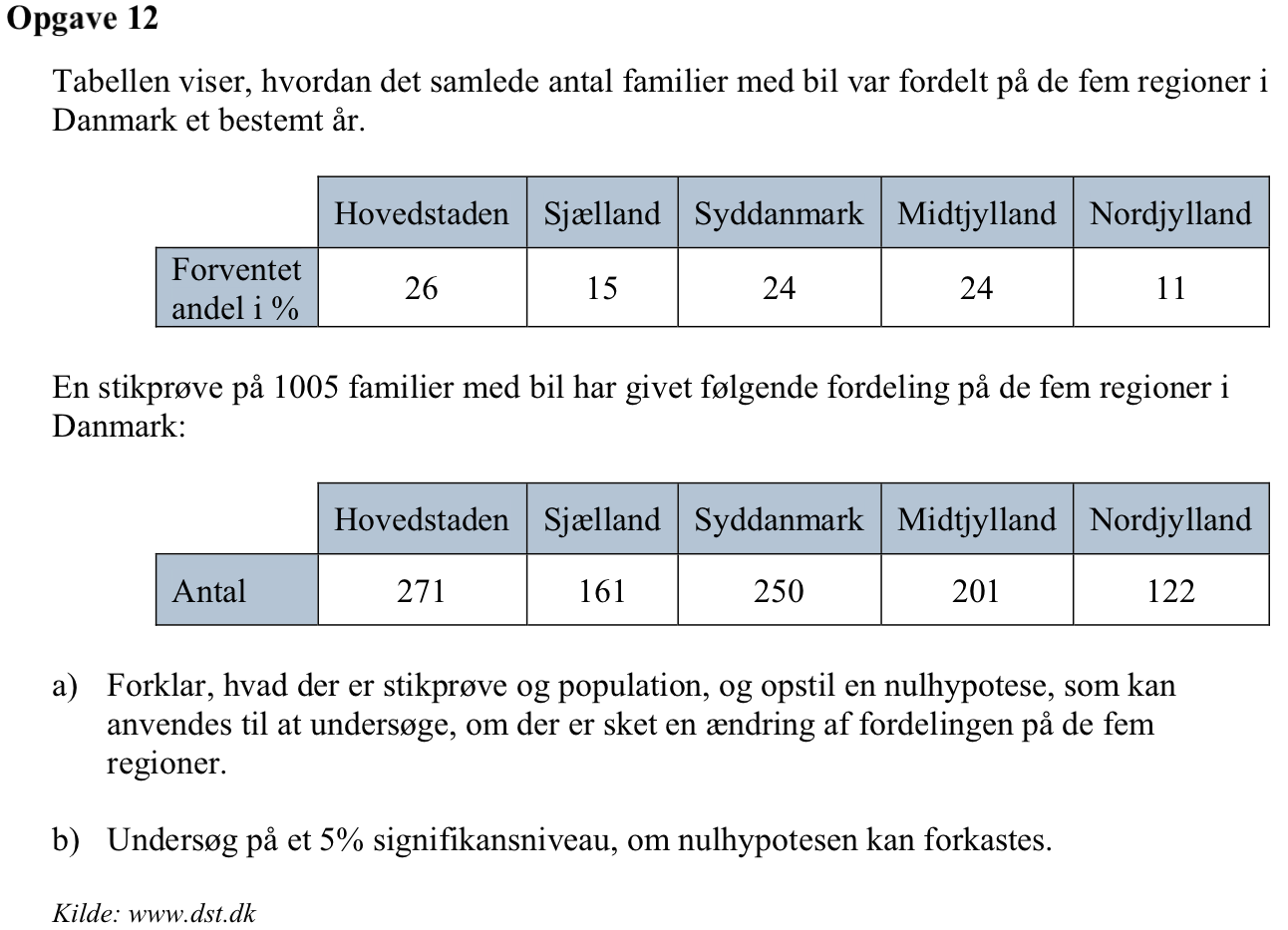
Svar på opgave 12:

Løsning i Ti-Nspire (uden regneark):

1. Det første skema er populationen udtrykt i %. Det andet skema er observeret stikprøve.

   Nulhypotesen er, at stikprøvens afvigelse fra populationen kan forklares ved tilfældigheder

2. Man opretter en liste med observerede hyppigheder:

   observeret:={271,161,250,201,122} ▸ {271,161,250,201,122}

   Man opretter en liste med forventede frekvenser:

   forventet_fre:={26%,15%,24%,24%,11%}*1. ▸ {0.26,0.15,0.24,0.24,0.11}

   Man opretter en liste med forventede hyppigheder som er lig med 1005 gange listen over forventede frekvenser:

   forventet_hyp:=sum(observeret)*forventet_fre ▸ {261.3,150.75,241.2,241.2,110.55}

   Man laver en chi-i-anden goodness-of-fit test på listerne observeret og forventet_hyp:

   χ²GOF observeret,forventet_hyp,4: stat.results ▸
   
   [["Titel","χ²-Goodness of Fit test"]
   ["χ²",9.2639889132426]
   ["PVal",0.054829285434625]
   ["df",4.]
   ["CompList","{...}"]]

   Man ser at PVal = 0,055 = 5,5%. Da dette er større end 5%, accepteres nulhypotesen.

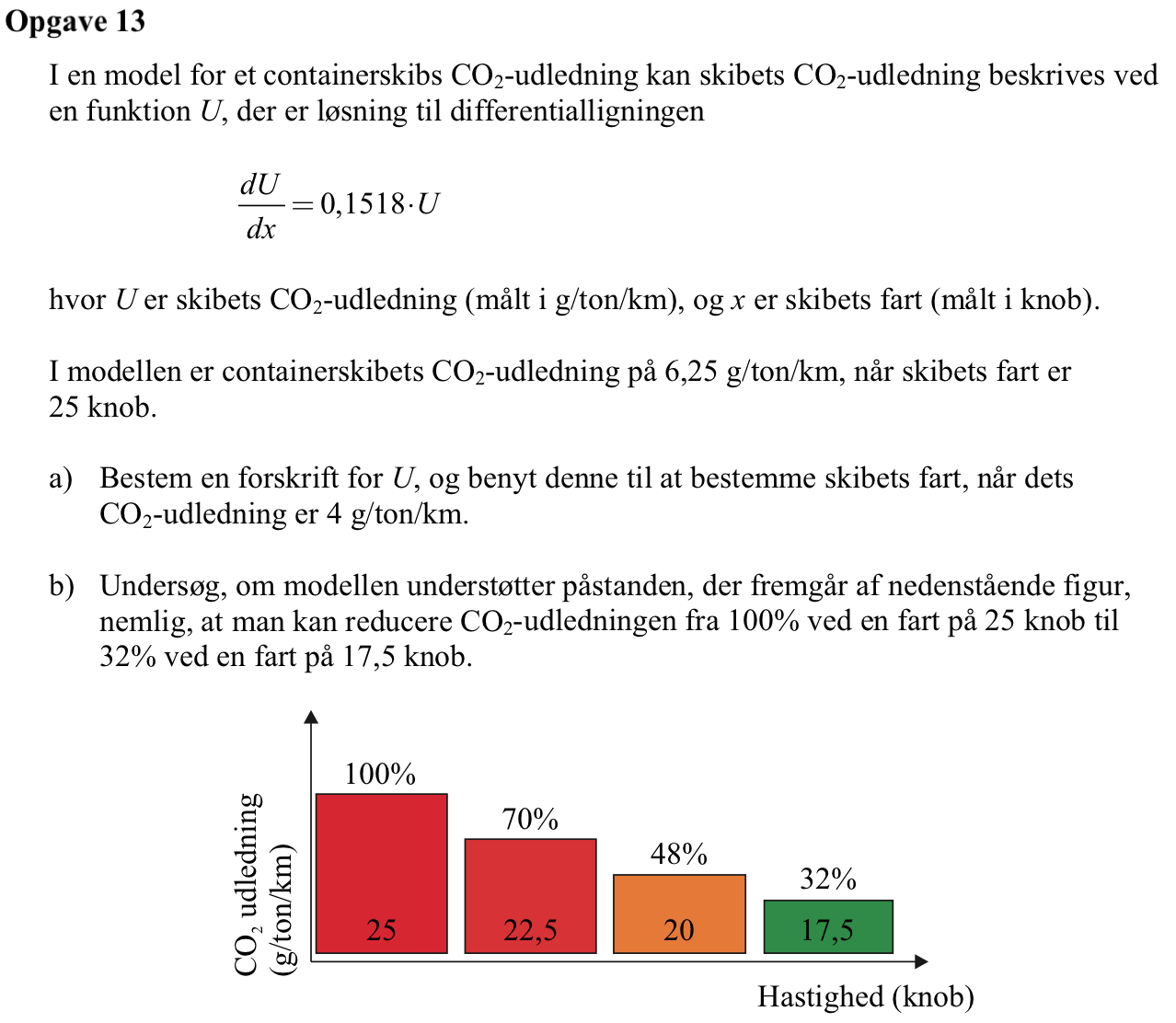
Svar på opgave 13:

Løsning i Ti-Nspire.

1. Man bruger desolve() kommandoen med startbetingelsen u(25) = 6,25:

   deSolve(u'=0.1518*u and u(25)=6.25,x,u) ▸ u=0.140518*(1.163927)^x

   Dette giver løsningen u(x) = 0,1405*(1,1639)^x

   Man skal finde det x, der er løsning til ligningen u(x) = 4. Man får:

   solve(0.140518*(1.163927)^x=4,x) ▸ x=22.060

   Dvs. 22 knob er den fart, der giver en CO₂-udledning på 4 g/ton/km.

2. Man skal udregne forholdet u(17,5)/u(25):

   (0.140518*(1.163927)^17.5/(0.140518*(1.163927)²⁵) ▸ 0.320

   Det ses, at forholdet er 0,32 = 32% og dermed er påstanden rigtig

Svar på opgave 14:

1. Omkredsen er 3x+2y.

   Arealet af trekanter er x²·(√3)/4, da trekanten er ligesidet og x dens sidelængde.

   Arealet af rektanglet er x·y

   Det samlede areal af figuren er x²·(√3)/4 + x·y

   Når x = 50 m og y = 100 m, er omkredsen 3·50 m + 2·100 m = 350 m

   Arealet med de samme værdier af x og y er 50²·(√3)/4 + 50·100 m² = 6082,5 m²

2. Omkredsen er 3x+2y = 200, dvs. y udtrykt ved x for den givne omkreds er:

   y = (200 - 3x)/2 = 100 - 3x/2

   Indsættes dette i formlen for arealet fås:

   Areal = T(x) = x²·(√3)/4 + x·y =

   x²·(√3)/4 + x·(200 - 3x)/2 =

   x²·(√3)/4 + 100x - 3x²/2 =

   ((√3)/4 - 3/2)·x² + 100x

3. Man finder først x med fMax() kommandoen i Ti Nspire

   fMax(((sqrt(3)/4)-(3/2))*x²+100.*x,x)|20≤x≤60 ▸ x=46.861

   Dvs x = 46,86 og y = 100 - 3·46,86/2 = 29,71

   Beregning af x i Maple: