Svar på opgave 1:

1. Toppunktet koordianter er (-b/(2·a),c-(b²/(4·a))) = (-(-8)/(2·2),15-(-8)²/(4·2)) = (2,7)

Svar på opgave 2:

1. 25000 er startværdien for t=0.

   1,03 er fremskrivningsfaktoren, som er det tal man ganger N(t) med hvert år.

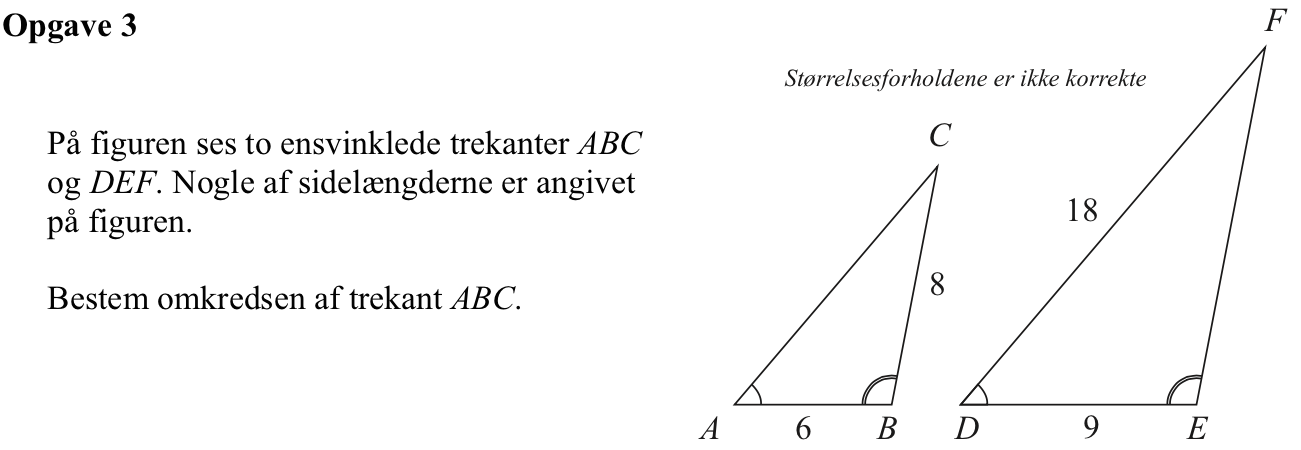
Svar på opgave 3:

1. Skaleringsfaktoren mellem de to ensvinklede trekanter er 6/9 = 2/3.

   |AC| = (2/3)·18 = 12. Omkredsen er 6 + 8 + 12 = 26

Svar på opgave 4:

1. En vilkårlig stamfunktion kaldes F(x). Man bruger integrationsreglen for polynomier (reglen for potensfunktioner plus reglen for summen af funktioner) og får: F(x) = 2·x³ + 3·x + k, hvor k er en konstant.

   Der gælder følgende krav til den søgte stamfunktion: F(2) = 10, som giver 2

   2·2³ + 3·2 + k = 10 ⇒

   16 + 6 + k = 10 ⇒

   k = -12

   Det giver stamfunktionen: F(x) = 2·x³ + 3·x - 12

Svar på opgave 5:

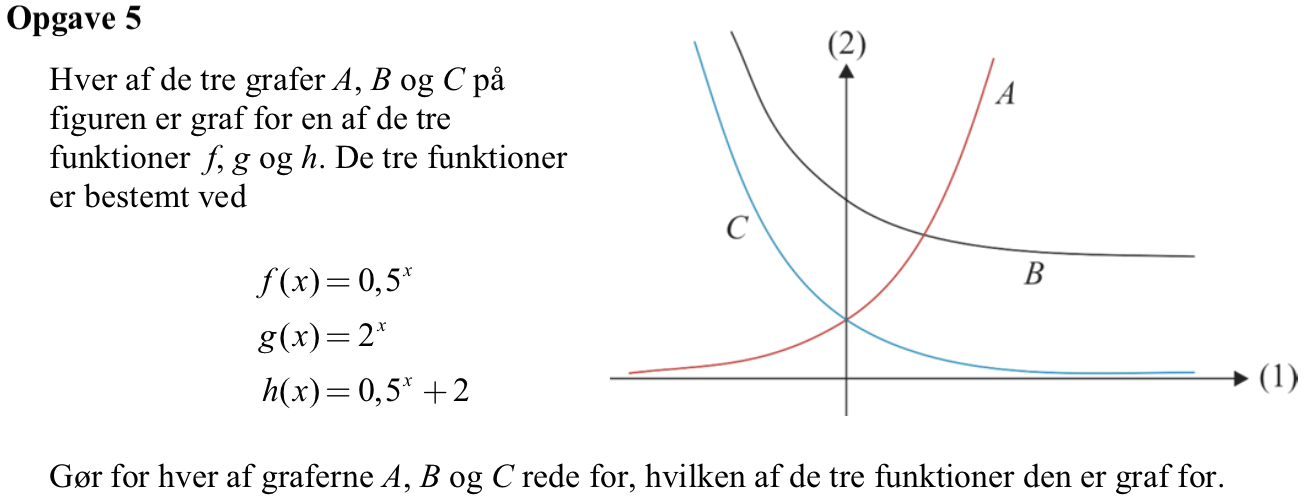
1. f(x) og g(x) er eksponentialfunktioner. h(x) er f(x) plus en positiv konstant.

   f(x) har en fremskrivningsfaktor mellem 0 og 1, mens g(x) har en fremskrivningsfaktor større end 1.

   Det betyder, at f(x) og h(x) er aftagende, mens g(x) er voksende.

   Da h(x) har værdier der er større end f(x) for alle x, får man at:

   A er graf for g(x)

   B er graf for h(x)

   C er graf for f(x)

Svar på opgave 6:

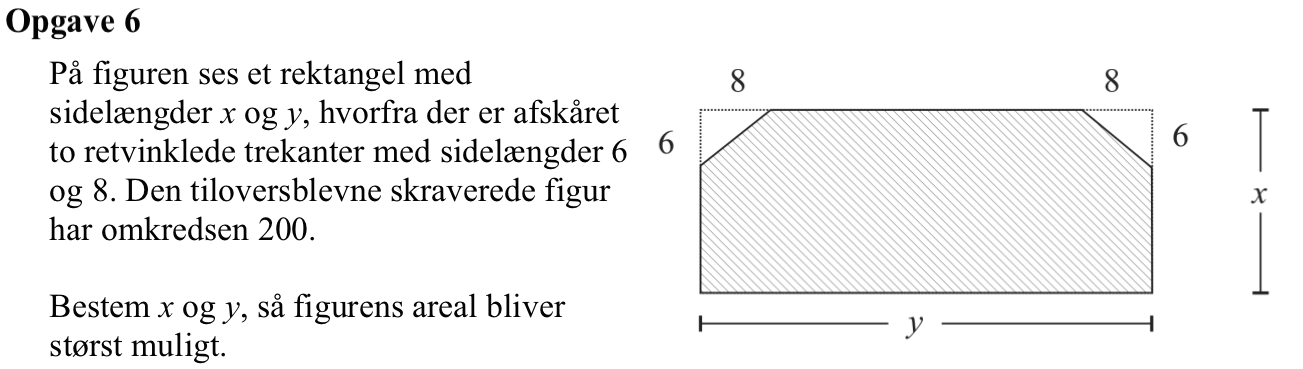
1. Omkredsen kan skrives: y + (x-6) + √[8² + 6²] + (y - 2·8) + √[8² + 6²] + (x-6) = 2·(x + y) - 8.

   Betinegelsen omkreds = 200 giver 2·(x + y) - 8 = 200 ⇒ y = 104 - x

   Arealet er x·y + 8·6 = x·y - 48. Man får følgende med betingelsen for omkredsen indsat i arealformlen:

   Areal = x·(104 - x) - 48 = -x² + 104·x - 48. Dette er en parabel med toppunkt og maksimum for x = -104/(-2) = 52. Dette giver y = 104 - 52 = 52.

   Dvs. man får det maksimale areal for x = y = 52

Svar på opgave 7:

1. Man opretter punkterne som stedvektorer:

   Vektoren AB = (5,10) - (20,5) = (-15,5)

   Man finder arealet af parallelogrammet som den numeriske værdi af determinanten af a og AB:

   |det(a,AB)| = |det((-1,2),(-15,5))| = |-5 - 2·(-15)| = |25| = 25

2. Projektionen af AB på a er

   a·(AB·a)/(|a|²) = (-1,2)·[(-15,5)·(-1,2)]/(1 + 4) = (-1,2)·[15+10]/5 = (-1,2)·5 = (-5,10)

Svar på opgave 8:

1. Man opretter listerne:

   motoreffekt:={1537,2003,2637,3489,4537,5755,7606} ▸ {1537,2003,2637,3489,4537,5755,7606}

   fart:={10,11,12,13,14,15,16} ▸ {10,11,12,13,14,15,16}

   Man bruger formlen for potens regression på to lister:

   PowerReg motoreffekt,fart,1: CopyVar stat.RegEqn,f1: stat.results

   [["Titel","Potensregression"]
   ["RegEqn","a*x^b"]
   ["a",1.1793548128832]
   ["b",0.29330525997458]
   ["r²",0.9965997312771]
   ["r",0.99829841794781]["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Heraf ses at a = 0,2933 og b = 1,179

   Bemærk at Ti-Nspire bruger a og b modsat opgaveteksten.

2. Man skal finde f(8000) = 1,179·8000^0,2933 = 16,46. Dvs skibet sejler med 16,5 knob

3. Man bruger formlen for procent-procent vækst for en potensfunktion og får:

   (1,3^0,2933 - 1)·100 % = 7.999 % = 8,0 %

Svar på opgave 9:

1. Grafen for f(x) er tegnet i Geogebra og vist nedenunder.

   

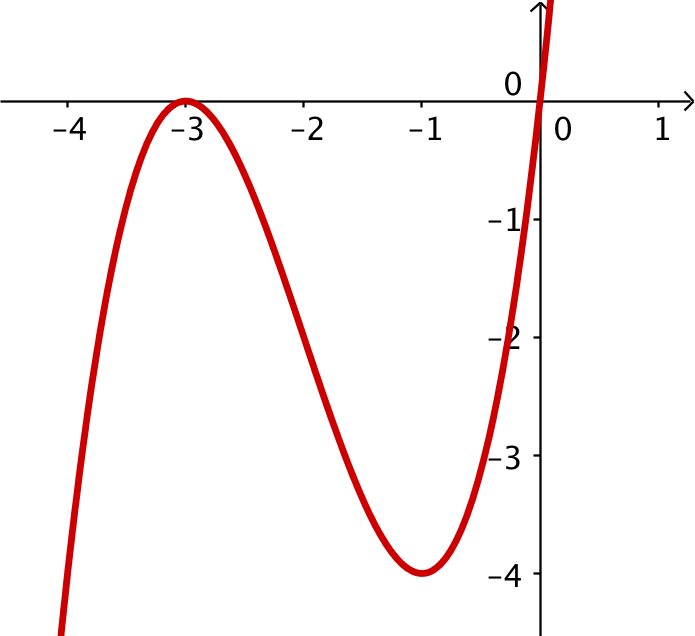
   For at bestemme nulpunkterne for f oprettes funktionen i Ti-Nspire og man bruger solve kommandoen:

   f(x):=x³+6*x²+9*x ▸ Udført

   solve(f(x)=0,x) ▸ x=−3 or x=0

2. Man finder fortegnene for f´(x):

   solve(derivative(f(x),x)<0,x) ▸ −3<x<−1

   solve(derivative(f(x),x)>0,x) ▸ x<−3 or x>−1

   Dvs. monotoniforholdene er

   f(x) vokser for x < -3

   f(x) aftager for -3 < x < -1

   f(x) vokser for x > -1

3. Man definerer først g(x):

   g(x):=−x²+b*x+c ▸ Udført

   Man bruger solve kommandoen med hensyn til b og c, idet g(1) = f(1) og g´(1) = f´(1):

   solve(f(x)=g(x) and derivative(f(x),x)=derivative(g(x),x),b,c)|x=1 ▸ b=26 and c=−9

   Dvs. b = 26 og c = -9

   For at finde tangenten bruger man kommandoen tangentLine

   tangentLine(f(x),x,1) ▸ 24*x-8

   Dvs. fællestangentens ligning er y = 24x - 8

Svar på opgave 10:

1. Først defineres r(t):

   r(t):=7.18*10⁻⁴*(t-0.93)²*(1-exp(0.464*(t-46.96))) ▸ Udført

   Man finder temperaturen for den maksimale væksthastighed med fMax kommandoen:

   fMax(r(t),t)|0≤t≤47 ▸ t=41.892

   Dvs. den temperatur hvor bakterierne vokser hurtigst er 42°C

Svar på opgave 11:

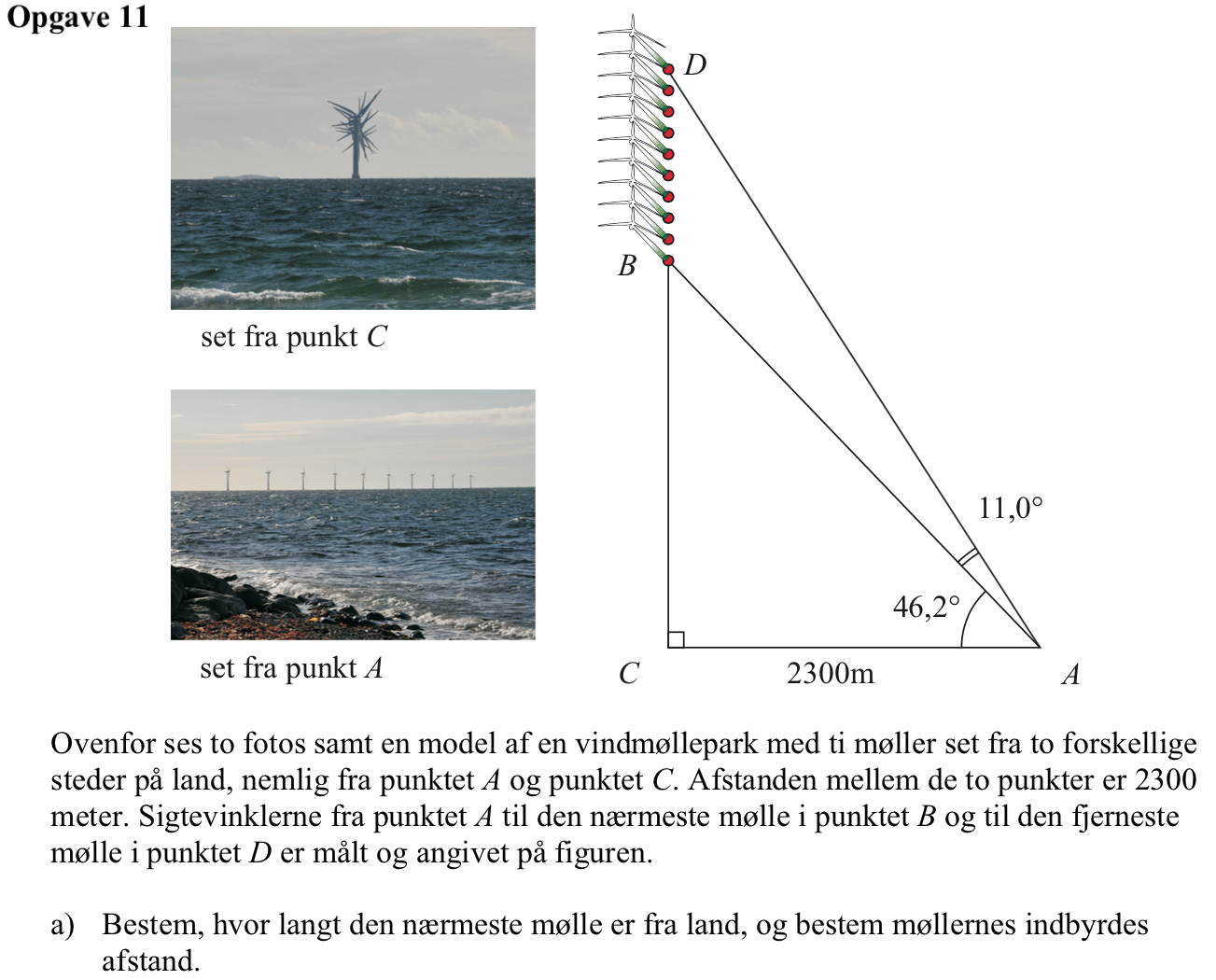
1. Afstanden fra den nærmeste vindmølle til land findes ved formlen:

   (2300 m)·tan(46,2°) = 2398,4 m

   Afstanden mellem B og D er (2300 m)·(tan(46,2° + 11°) - tan(46,2°)) = 1170,5 m

Svar på opgave 12:

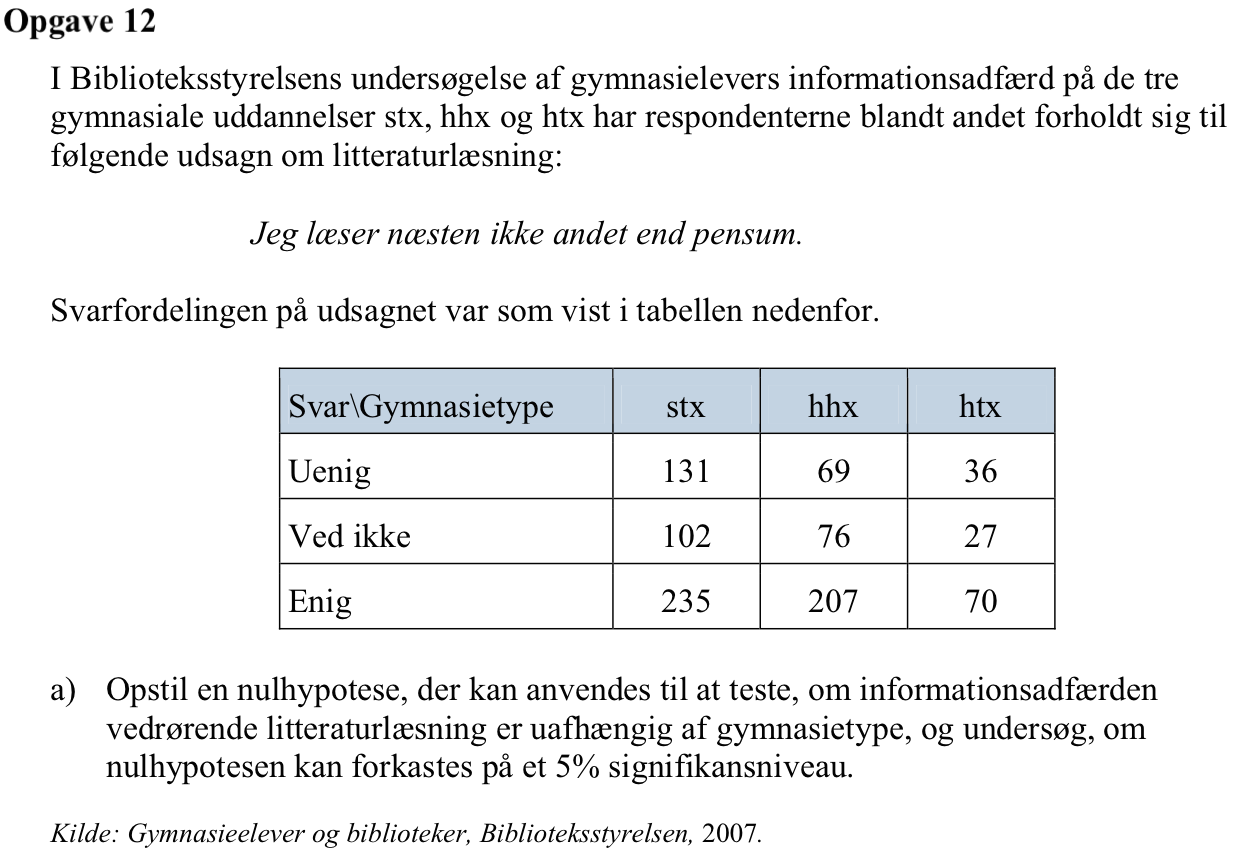
1. Nulhypotesen er, at svar er uafhængig af gymnasietype.

   En matrice med observerede data oprettes:

   

   Man laver en chi-i-anden uafhængighedstest med 4 frihedsgrader på matricen med kommandoen:

   χ²2way observeret: stat.results ▸

   [["Titel","χ²-uafhængighedstest"]
   ["χ²",8.9454934213077]
   ["PVal",0.062476419629179]
   ["df",4.]
   ["ExpMatrix","[...]"]
   ["CompMatrix","[...]"]]
   

   Det ses at PVal = 0,062 = 6,2 %. Da dette er større end 5 %, godkendes nulhypotesen.

Svar på opgave 13:

1. Man definerer punterne A til D som stedvektorer:

   a:=[16,16,0] ▸ [16,16,0]

   b:=[−16,16,0] ▸ [−16,16,0]

   c:=[−16,−16,0] ▸ [−16,−16,0]

   d:=[16,−16,0] ▸ [16,−16,0]

   r:=[−27,−16,23] ▸ [−27,−16,23]

   ab:=b-a ▸ [−32,0,0]

   rxab:=crossP(r,ab) ▸ [0,−736,−512]

   Man dividerer igennem med største fælles divisor 32:

   n:=((rxab)/(32)) ▸ [0,−23,−16]

   dotP(n,[x,y,z]-a)=0 ▸ −23*y-16*z+368=0

   Dvs. planen αs ligning er −23y - 16z + 368 = 0

2. Man finder T som skæringspunktet mellem linjen l og planen β:

   solve(23*x-5*z+368=0 and x=16-27*s and y=16-16*s and z=23*s,s) ▸ s=1 and x=−11 and y=0 and z=23

   Dvs. toppunktet T = (-11,0,23)

3. Man finder β's normalvektor ud fra dens ligning: 23x + 0y + (-5)z + 368 = 0:

   m:=[23,0,−5] ▸ [23,0,−5]

   solve(cos(x*1.°)=−abs(dotP(n,m))/(norm(n)*norm(m)),x)|0<x<180 ▸ x=96.97

   Dvs. dens stumpe vinkel mellem α og β er 97°

Svar på opgave 14:

1. Funktionen defineres:

   f(x):=exp(−0.1*x)*sin(π*x)|0<x<3 ▸ Udført

   Ekstremumspunkterne beregnes ved at sætte f´(x) = 0:

   solve(derivative(f(x),x)=0,x) ▸ x=0.48987 or x=1.48987 or x=2.48987

   x₁ = 0,489871 og x₂ = 2,489871.

   Det giver punkterne A = [0,4899;f(0,4899)] = (0,490;0,952)

   B = [2,490;f(2,490)] = (2,49;0,779)

2. Man definerer g(x):

   g(x):=b*a^x ▸ Udført

   Man finder a og b så g(0.489871)=0.951711 og g(2.489871)=0.779195:

   solve(g(0.489871)=0.951711 and g(2.489871)=0.779195,a,b) ▸
    a=−0.904837 and b=0.0317997-0.998987*i or a=0.904837 and b=0.99949

   Den gyldige (reelle) løsning er a=0,904837 and b=0,99949. Dvs. g(x) = 0,999·0,905^x

3. Man skal finde integralet af |f(x)| fra x₁ = 0,48987 til x₂ = 2,48987.

   integral(abs(f(x)),x,0.48987,2.48987) ▸ 1.0996

   Dvs. arealet er 1,0996

Svar på opgave 15:

1. Man løser differentialligningen ved hjælp af desolve kommandoen:

   deSolve(m'=−k*m² and m(0)=70,t,m) ▸ (1/70)-(1/m)=−k*t

   Herefter findes k ved hjælp af solve:

   solve((1/70)-(1/m)=−k*t,k)|m=20 and t=60. ▸ k=5.952

   Man isolerer m ved hjælp af solve-kommandoen:

   solve((1/70)-(1/m)=−k*t,m)|k=0.000595238 ▸ m=(1680.)/(t+24.)

   Dvs. k = 5,952 og M(t) = m=(1680.)/(t+24.)

2. M'(60) er ændringen af massen af stoffet A efter 60 minutter. M'(60) findes ved kommandoen:

   derivative((1680.)/(t+24.),t)|t=60 ▸ −0.238095

   Dvs. M'(60) = −0.238 mg/min.. Minustegnet viser, at massen aftager.