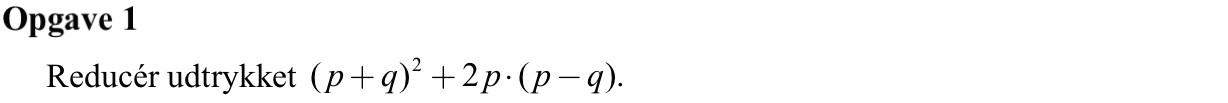
Svar på opgave 1:

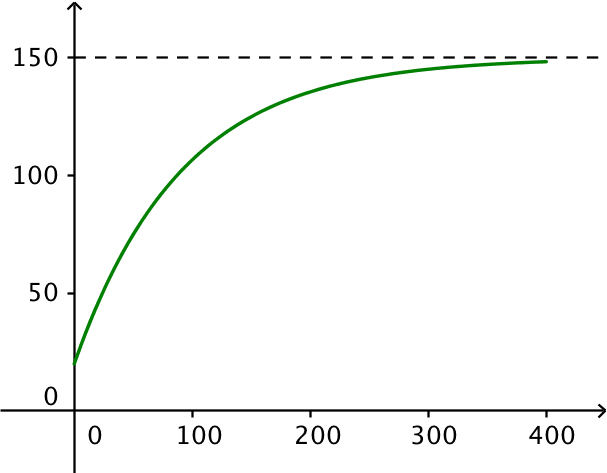
1. (p + q)² + 2·p·(p - q) =

   p² + 2·p·q + q² + 2·p² - 2·p·q =

   p² + 2·p² + 2·p·q - 2·p·q + q² =

   3p² + q²

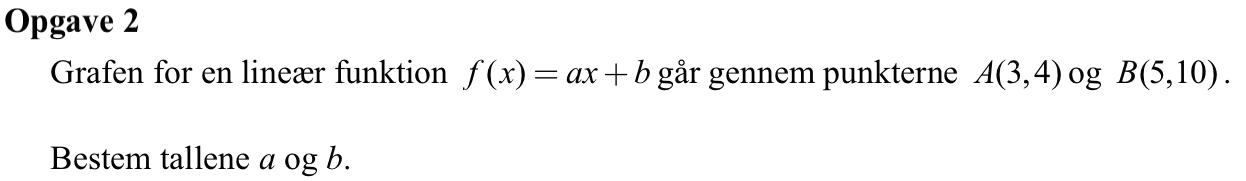
Svar på opgave 2:

1. At grafen for f(x) går gennem punkterne (3,4) og (5,10) betyder, at f(3) = 4 og f(5) = 10, dvs. man har to ligninger med hensyn til de to ubekendte a og b:

   a·3 + b = 4 ∧ a·5 + b = 10 ⇔

   a = (4 - b)/3 ∧ [(4 - b)/3]·5 + b = 10 ⇔

   a = (4 - b)/3 ∧ 20/3 - 5·b/3 + b = 10 ⇔

   a = (4 - b)/3 ∧ - 2·b/3 = 10 - 20/3 ⇔

   a = (4 - b)/3 ∧ b = -(3/2)·10/3 ⇔

   a = (4 - (-5))/3 ∧ b = -5 ⇔

   a = 9/3 ∧ b = -5 ⇔

   a = 3 ∧ b = -5

Svar på opgave 3:

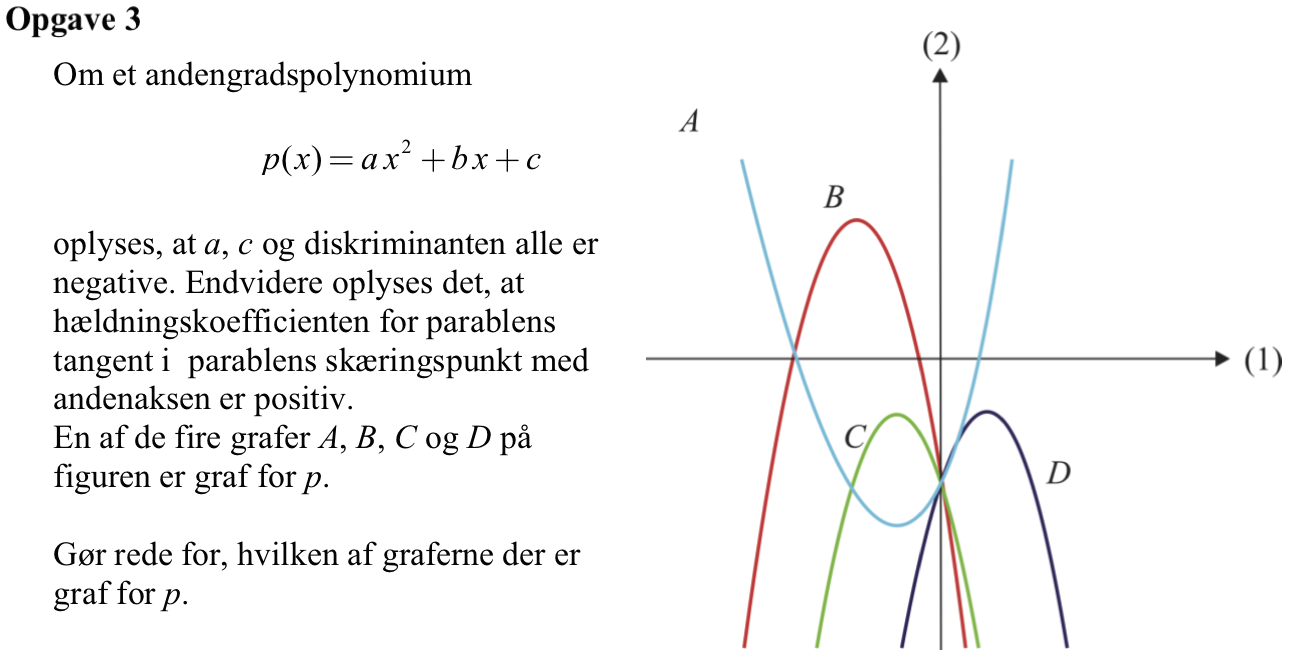
1. At a er negativ betyder, at parablens grene vender nedad.

   At c er negativ betyder, at parablen skærer den negative del af y-aksen.

   At diskriminanten er negativ betyder, at parablen ikke skærer x-aksen.

   Ovenstående er opfyldt for C og D, men kun D har en positiv hældning i skæringspunktet med y-aksen.

   Dermed er D graf for p(x)

Svar på opgave 4:

1. Arealet er integralet af f(x) fra x=0 til x=3. Stamfunktionen til f(x) kaldes F(x) og er lig med:

   -(1/4)·x⁴ + (9/2)·x² + k, hvor k er en konstant.

   Areal = F(3) - F(0) = -(1/4)·3⁴ + (9/2)·3² + k - [-(1/4)·0⁴ + (9/2)·0² + k] =

   -81/4 + 81/2 + k - [0 + k] = 81/4 = 20,25

   Dvs. arealet af M er 20,25

Svar på opgave 5:

1. f(x) er en voksende funktion, da den er summen af to voksende funktioner: g(x) = e^x og h(x) = 7·x.

Svar på opgave 6:

1. Cirklens ligning er x² + y² = 2

   Man sætter linjes værdier for x og y ind i cirklens ligning.

   x = 3 + t og y = - 3 - t.

   Dette indsættes i cirklens ligning, og man løser de fremkomne ligninger med hensyn til t:

   x² + y² = 2 ⇒

   (3+t)² + (-3-t)² = 2 ⇒

   (3+t)² + (-1)²·(3+t)² = 2 ⇒

   2·(3+t)² = 2 ⇒

   (3+t)² = 1 ⇒

   (3+t) = ± 1 ⇒

   t = -3 ± 1 ⇒

   t = -4 ∨ t = -2

   Værdierne for t indsættes i udtrykkene for x og y:

   t = -4: x = 3 + (-4) = -1 og y = - 3 - (-4) = 1.

   t = -2: x = 3 + (-2) = 1 og y = - 3 - (-2) = -1.

   Dvs. skæringspunkterne er (x,y) = (-1,1) og (x,y) = (1,-1)

Svar på opgave 7:

1. Man opretter listerne:

   år:={1990,1995,2000,2005,2006,2007,2008,2009,2010,2011}-1990 ▸ {0,5,10,15,16,17,18,19,20,21}

   procentdel:={3.1,4.5,6.5,10.4,11.8,14.5,15.2,16.6,18.1,20.} ▸ {3.1,4.5,6.5,10.4,11.8,14.5,15.2,16.6,18.1,20.}

   Man bruger formlen for eksponentiel regression på to lister:

   ExpReg år,procentdel,1: CopyVar stat.RegEqn,f1: stat.results ▸

   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",2.8833056512832]
   ["b",1.0952169904757]
   ["r²",0.99158852581637]
   ["r",0.99578538140323]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Heraf ses at a = 1,0952 og b = 2,8833

   Bemærk at Ti-Nspire bruger a og b modsat opgaveteksten.

2. Konstanten a er fremskrivningsfaktoren som tallet fra det gamle år skal ganges med for at give tallet for det nye.

   Fordoblingskonstanten er ln(2)/ln(a) år = ln(2)/ln(1,0952) år = 7,62 år

3. Man definerer funktionen P(x) i Ti-Nspire:

   p(x):=2.88331*1.09522^x ▸ Udført

   Man finder værdien for årstallet 2020:

   p(2020-1990) ▸ 44.15

   Dvs. modellen forudsiger at 44,2 % af elforbruget dækkes af vedvarende energi i 2020. Dermed er forudsigelsen realistisk.

Svar på opgave 8:

1. Tangentlinjen til funktionen gennem punktet P = (5,f(5)) findes på følgende måde:

   f(x):=ln(x)+x²|x>0 ▸ Udført

   y=tangentLine(f(x),x,5.) ▸ y=10.2*x-24.39056

   Dvs. at tangenten gennem P har ligningen y = 10,2x - 24,39

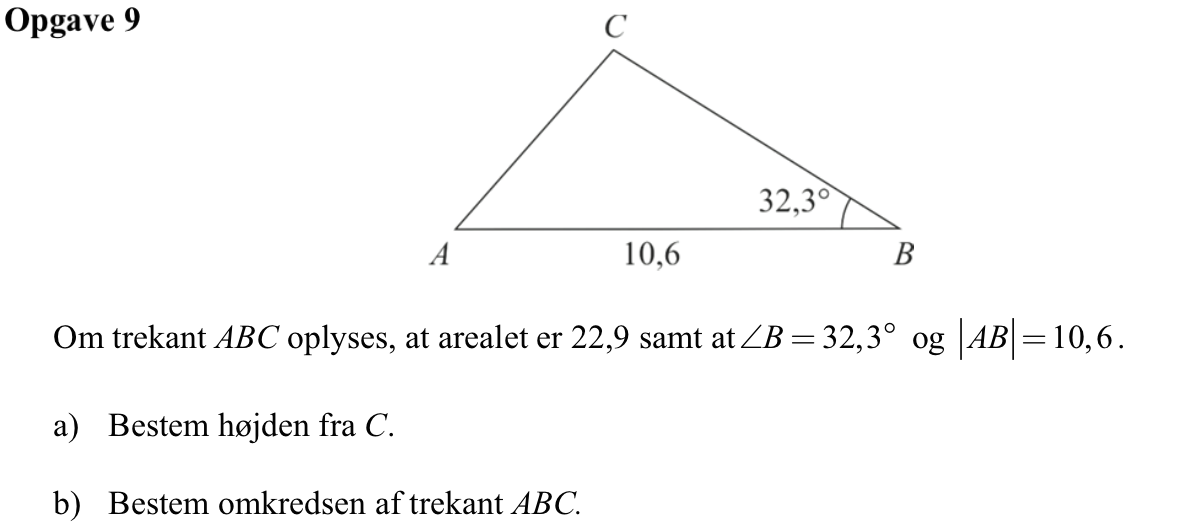
Svar på opgave 9:

1. Højden fra C på AB kaldes h_c. Der gælder at 0,5·h_c·|AB| = arealet af trekanten. Dette giver: 0,5·h_c·10,6 = 22,9 ⇒ h_c = (22,9·2)/10,6 = 4,32

2. For at finde omkredsen skal man finde |BC| og |AC|. Om |BC| ved man at |BC|·sin(∠C) = h_c ⇒ |BC| = h_c/sin(∠C). Det giver at |BC| = 4,32/sin(32,3°) = 8,084. Man kan nu finde |AC| ved hjælp af en cosinusrelation: cos(∠C) = (|AB|² + |BC|² - |AC|²)/(2·|AB|·|BC|).

   Denne løses med kommandoen:

   solve(cos(32.3*1.°)=(10.6²+8.08²-x²)/(2*10.6*8.08),x)|x>0 ▸ x=5.732

   Dvs. |AC| = 5,732. Omkredsen bliver dermed: 10,6 + 8,084 + 5,732 = 24,4

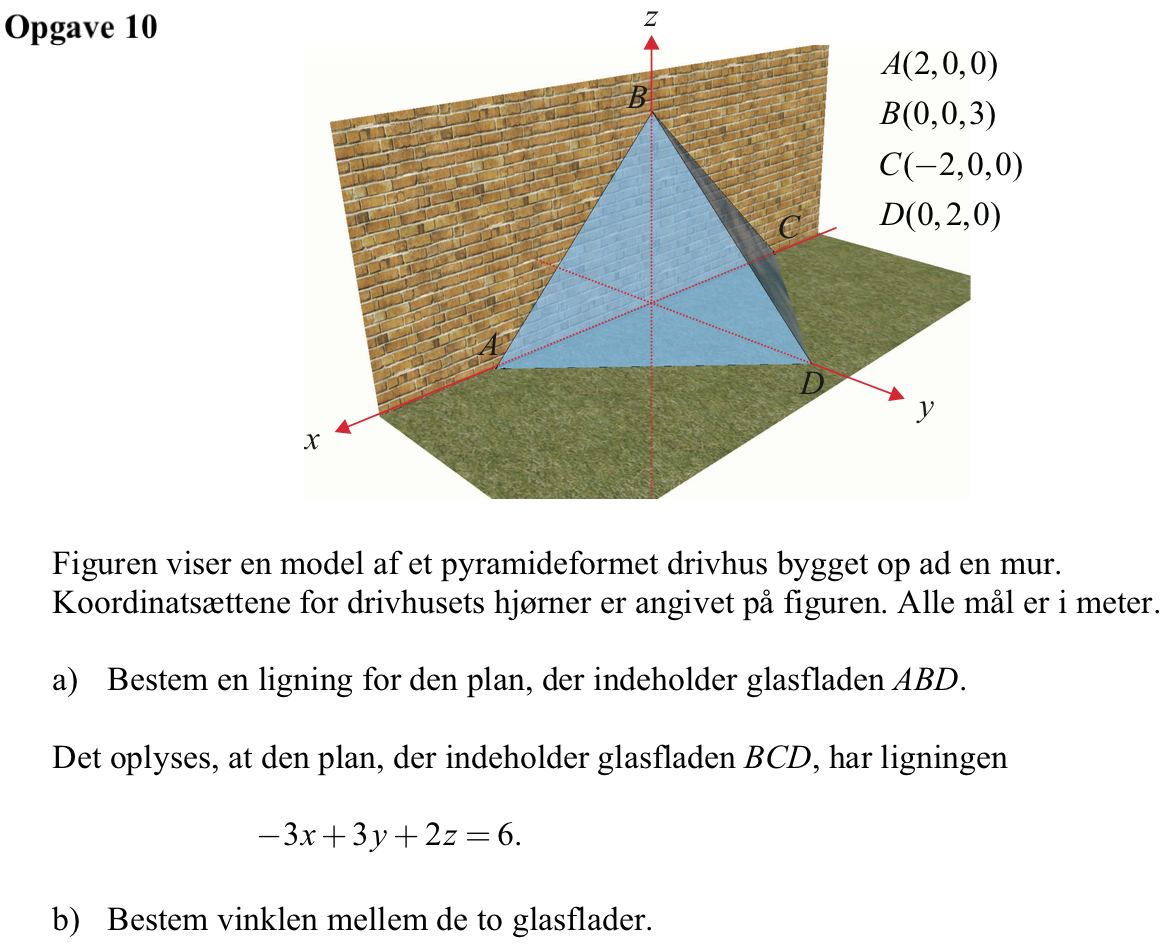
Svar på opgave 10:

1. Intuitiv løsning:

   De to glasflader er hinandens spejlbillede i yz-planen. Dermed kan man komme fra et punkt i den ene glasflade til et punkt i den anden ved at skifte fortegn på x-koordinaten til punktet. Dette gælder f.eks. for A = (2,0,0) og C = (-2,0,0).

   Ligningen for den plan, der indeholder BCD, er -3x + 3y +2z = 6. Dermed er ligningen for den plan, der indeholder ABD den samme blot med modsatte koefficient til x, dvs. 3x + 3y + 2z = 6

   Prøve: man indsætter punkterne A = (2,0,0), B = (0,0,3) og D = (0,2,0) i ligningen for at se, om den stemmer:

   A: 3·2 + 3·0 + 2·0 = 6 OK, B: 3·0 + 3·0 + 2·3 = 6 OK og D: 3·0 + 3·2 + 2·0 = 6 OK

   Løsning i Ti-Nspire:

   Man defnerer punkterne A, B, C og D som stedvektorer:

   a:=[2,0,0] ▸ [2,0,0]

   b:=[0,0,3] ▸ [0,0,3]

   c:=[-2,0,0] ▸ [-2,0,0]

   d:=[0,2,0] ▸ [0,2,0]

   Man definerer vektorerne AB og AD:

   ab:=b-a ▸ [-2,0,3]

   ad:=d-a ▸ [-2,2,0]

   Man opretter normalvektoren n til planen som krydsproduktet af vektor AB og vektor AD:

   n:=crossP(ab,ad) ▸ [−6,−6,−4]

   Et tilfældigt punkt P = (x,y,z) oprettes: p:=[x,y,z] ▸ [x,y,z]

   Vektoren AP oprettes: ap:=p-a ▸ [x-2,y,z]

   Punkterne i planen opfylder, at skalarproduktet af n og AP er lig med nul. Dette indsættes i Ti-Nspire:

   dotP(n,ap)=0 ▸ 3*x+3*y+2*z-6=0

   Heraf fås at planens ligning er 3x + 3y + 2z - 6 = 0

2. Man finder vinklen mellem glasfladerne som vinklen mellem de to planers normalvektorer. Normalvektoren til den plan, som indeholder BCD, kaldes m. Dens koordinater aflæses af planens ligning til m = (−3,3,2), dvs. koefficienterne til x, y og z i ligningen.

   m oprettes som vektor i Ti-Nspire: m:=[−3,3,2] ▸ [−3,3,2]

   Vinklen mellem planerne findes som vinklen mellem deres normalvektorer. Dette gøre med kommandoen:

   solve(cos(x*1.°)=(dotP(n,m)/(norm(n)*norm(m)),x)|0<x<180 ▸ x=79.52

   Der er to vinkler mellem de to planer. Den ene er 79,5° som fundet ovenfor, mens den anden er 180° - 79,5° = 100,5°. Hvilken en, som man skal vælge, ses i Geogebra:

   

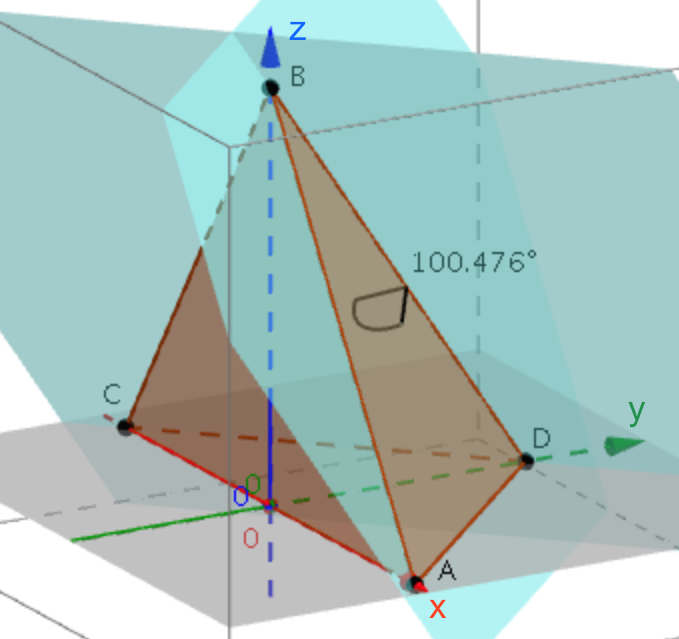
   Det ses, at 100,5° er vinklen mellem glasfladerne.

Svar på opgave 11:

1. Der oprettes to lister med observerede og forventede værdier.

   observeret:={9,19,15,10,7} ▸ {9,19,15,10,7}

   forventet:=sum(observeret)*{1/5,1/5,1/5,1/5,1/5} ▸ {12,12,12,12,12}

   Man skal lave en goodness of fit test. Det skyldes, at man skal sammenligne nogle observerede data med nogle forventede. De observerede data grupperes efter slikkets farve.

   De forventede antal beregnes i dette tilfælde ud fra de observerede ved at gange summen af observationer (60) med sandsynligheden (1/5). Dette giver, at det forventede antal af hver farve slik er 12. Der er 4 frihedsgrader for Chi-i-anden fordelingen, da der er 5 grupper.

   Nulhypotesen er, at alle farver slik forekommer lige hyppigt, og at afvigelser fra det forventede kan forklares med tilfældigheder.

   χ²GOF observeret,forventet,4: stat.results ▸

   

   (Kommandoen findes under menuen: Beregninger ▸ Statistik ▸ statistiske tests ▸ χ²-Goodness of Fit test...)

   Det ses at PVal = 0,092 = 9,2 %, som er større end 5 % og dermed accepteres nulhypotesen.

Svar på opgave 12 (London Eye):

1. Nedenstående graf er tegnet i Geogebra. (Kode: f(x) = Hvis[0 ≤ x ≤ 30, 67.5sin(0.209x - 1.57) + 70])

   

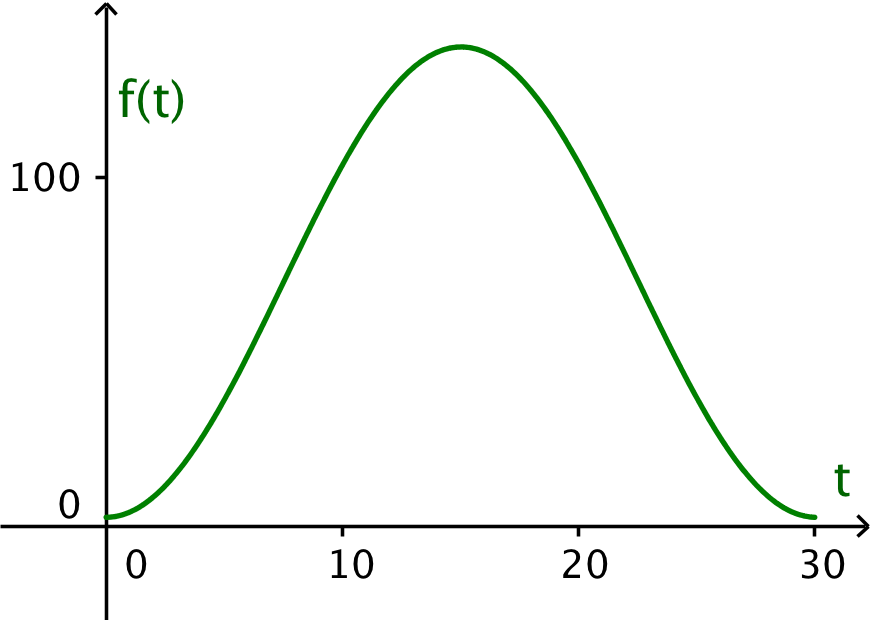
   Gondolens højde over jorden efter 7 minutter = f(7) = 67,5·sin(0,209·7 - 1,57) + 70 meter = 62,8 meter

2. Man skal løse ligningen f(t) = 40 for t liggende mellem 0 og 30 minutter. Nedenunder er løsningen vist grafisk.

   

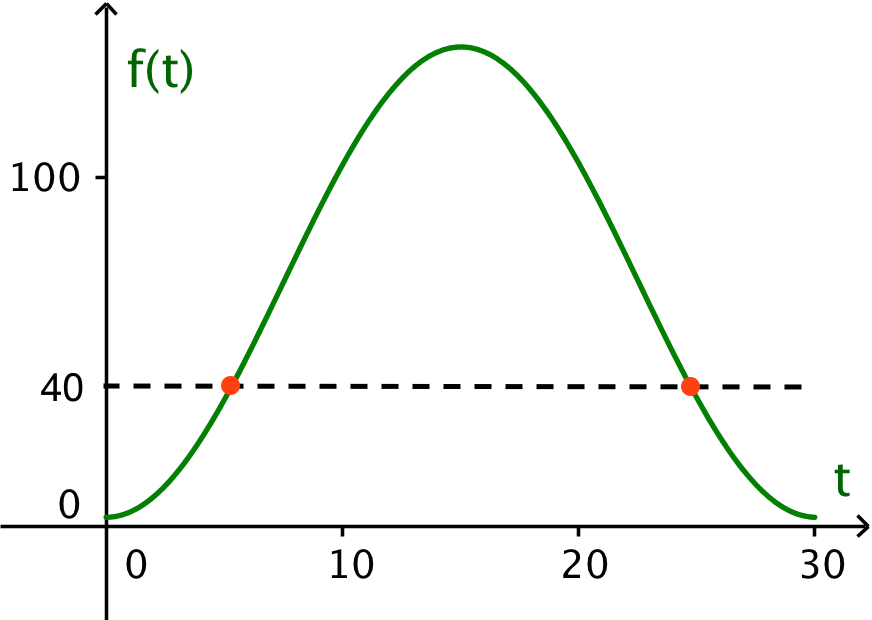
   Man skal finde x-værdierne til de to røde punkter og dernæst vælge den mindste. Dette gøres med følgende kommando:

   solve(f(t)=40,t)|0<t<30 ▸ t=5.30835 or t=24.7471

   Det ses heraf, at gondolen når højden 40 meter første gang efter 5,3 minutter

Svar på opgave 13:

1. Væksthastigheden er dN/dt og findes ved at indsætte N(t)=500 på højre side i differentialligningen. Man får dN/dt = 0,0029·500·(1500-500) = 0,0029·500·1000 = 1450

   Dvs. væksthastigheden er 1450 traner/år

2. Forskriften for tranebestandens størrelse, N(t), findes ved kommandoen:

   deSolve(n'=0.00029*n*(1500-n) and n(0)=194,t,n) ▸ n=1500.*(1.54496)^t/((1.54496)^t+6.73196)

   Dvs. N(t) = 1500·1,545^t/(1,545^t + 6,732) traner

3. Der er tale om logistisk vækst, dvs. en vækst på formlen: y' = a·y·(b - y). For denne type vækst gælder, at væksten er størst når y = b/2. Dette svarer her til, at tranebestanden vokser hurtigst ved N(t) = 1500/2 traner ⇒ N(t) = 750 traner. Denne ligning løses med hensyn til t:

   solve(1500.*(1,545)^t/((1,545)^t+6.73196)=750,t) ▸ t=0.43836

   Den maksimale vækst hastighed for tranerne opnås til tidspunktet t = 4,4 år

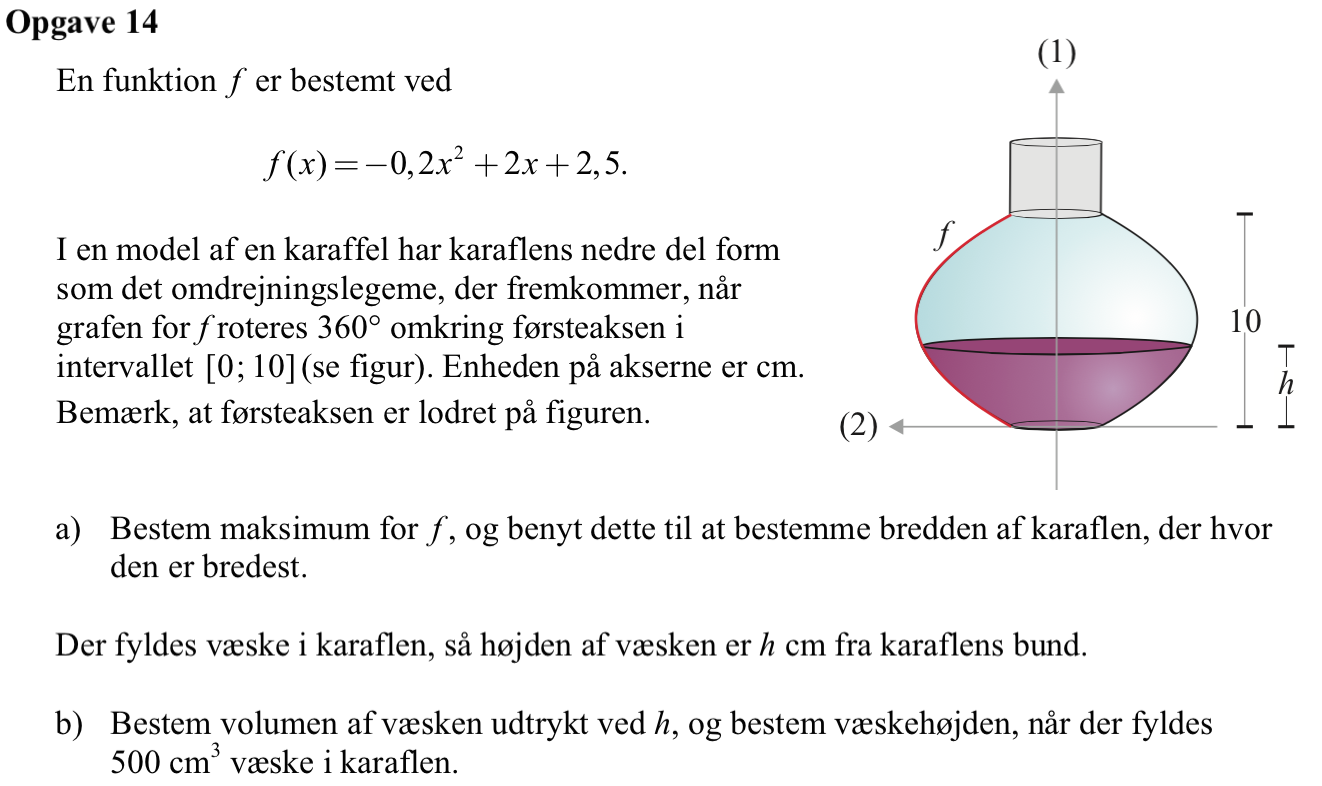
Svar på opgave 14:

1. Man opretter funktionen f og og finder maksimum for funktionen i intervallet 0≤x≤10.

   f(x):=−0.2*x^(2)+2*x+2.5 ▸ Udført

   fMax(f(x),x) ▸ x=5. (Den x-værdi, hvor funktionen har maksimum)

   2*f(5) ▸ 15.

   Maksimum for funktionen er 15 og karaflens maksimale tykkelse er dermed 2·15 = 30

2. Man skal bruge formlen for rumfanget af et omdrejningslegeme omkring x-aksen. Her skal man finde det h, der indsat som øvre grænse i integralet, giver rumfanget 500. Man bruger følgende kommando i Ti-Nspire:

   solve(π*integral(f(x)²,x,0,h)=500,h) ▸ h=4.6061

   Dvs. den væskehøjde, der giver rumfanget 500 cm³ er 4,6 cm

Svar på opgave 15:

1. BC er en katete i en retvinklet trekant, hvor hypotenusen er 7 og den anden katete er x. Der blive |BC| i følge Pythagoras læresætning lig med √(7² - x²) dvs. |BC| = √[49 - x²]

   d er højden i en retvinklet trekant med kateterne x og √(49 - x²) samt hypotenusen 7. For en retvinklet trekant gælder at arealet af den kan beregnes på to måder: en halv højde gange grundlinje og en halv gange produktet af de to kateter. Dvs.

   Areal af trekant ABC = 0,5·d·7 = 0,5·x·√(49 - x²) ⇒ d = (x/7)·√[49 - x²]

2. Man opretter d som funktion af x i Ti-Nspire.

   d(x):=x*(√(49-x²))/7 ▸ Udført

   Man finder det x, som giver maksimum værdien for d, med kommandoen:

   fMax(d(x)*1.,x) ▸ x=4.9497

   Dvs. x = 4,95 giver den største værdi af d.

   Det kan også indses ved hjælp af symmetri: Når x vokser fra 0 bliver d større og BC mindre indtil det punkt, hvor x = |BC|. Herfra vil længderne af x og BC være byttet om og d vil blive mindre igen. Den største værdi af d indtræder derfor, når x = |BC|, hvilket vil sige x = 7/√2 = 4,95.

Svar på opgave 16:

1. Man ved, at ændringen i stegens temperatur dT(x)/dx er proportional med forskellen mellem stegens temperatur og 150 °C. Proportionalitetskonstanten er 0,011. Det giver differential­ligningen:

   dT(x)/dx = 0,011·(150 - T(x))

   Man kan evt. tilføje en startbetingelse: temperaturen er 20° i starten, dvs til x = 0. Man kan evt. også tilføje, at modellen kun gælder i et bestemt tidsinterval f.eks. 0 < x < 400 minutter. Nedenfor er vist en løsning lavet i Geogebra med disse betingelser.