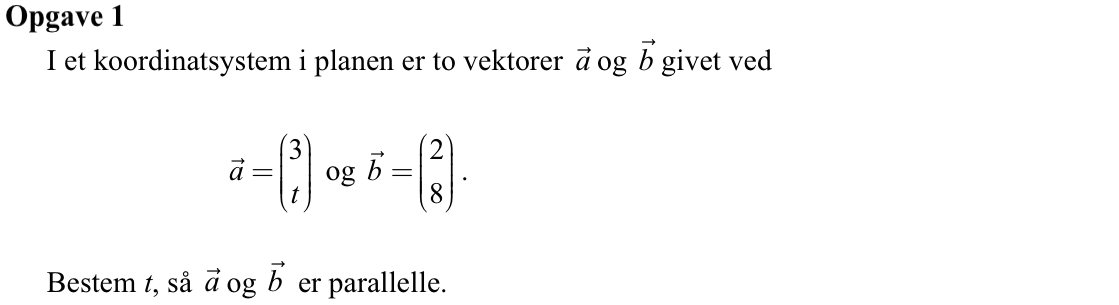
Svar på opgave 1:

1. Man kan finde t på to måder: enten ved at benytte, at det(a,b) = 0, eller ved at benytte, at vektorerne skal være proportionale. Det sidste vil sige, at forholdet mellem førstekordinaterne i hver vektor skal være lig med forholdet mellem andenkoordinaterne.

   Man bruger den anden metode og får, at 3/2 = t/8 ⇒t = 8·(3/2) = 12.

   Dermed er den værdi af t, som gør, at vektorerne er parallelle, lig med 12

Svar på opgave 2:

1. Førstekoordinaterne til parablens skæringspunkter med førsteaksen er det samme som rødderne i andengradspolynomiet p(x).

   Dette er igen det samme som løsningen til ligningen p(x) = 0. Man får:

   p(x) = 0 ⇒ x² - 10x + 24 = 0 ⇒

   x = 10/2 ± (1/2)·√(100 - 4·24) ⇒

   x = 5 ± (1/2)·√(100 - 96) ⇒

   x = 5 ± (1/2)·√4 ⇒

   x = 5 ± (1/2)·2 ⇒

   x = 5 ± 1 ⇒

   x = 4 ∨ x = 6

   Derfor er førstekoordinaterne x = 4 og x = 6

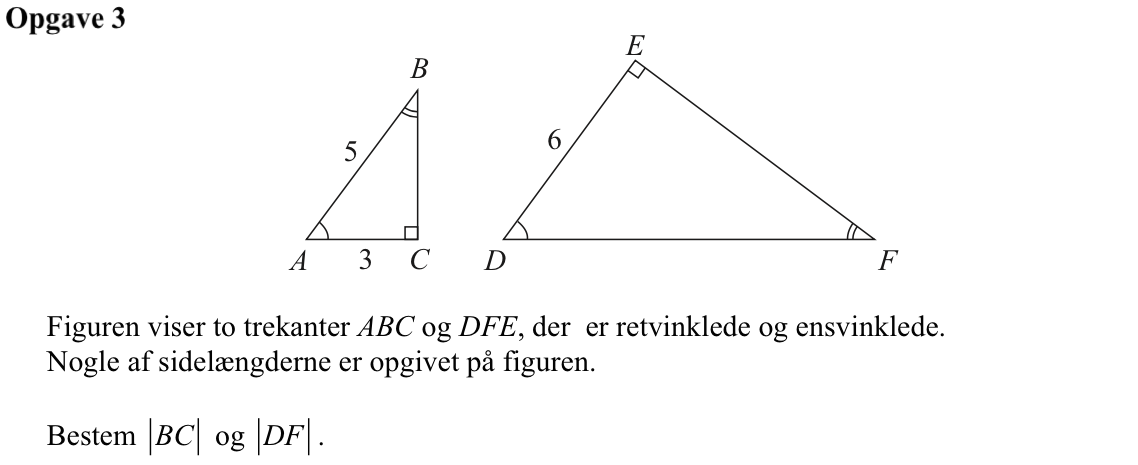
Svar på opgave 3:

1. |BC| findes ved hjælp af Pythagoras læresætning:

   |BC|² + 3² = 5² ⇒

   |BC|² = 5² - 3² ⇒

   |BC|² = 25 - 9 ⇒

   |BC|² = 16 ⇒

   |BC| = √16 = 4

   |DF| findes ved at gange den ensliggende side i trekant ABC med skaleringsfaktoren mellem de to trekanter. Skaleringsfaktoren er |ED|/|AC| = 6/3 = 2. AB er den side i trekant ABC som er ensliggende med side DF i trekant DEF. Det ses af at AB og DF begge er hypotenuser.

   Dermed bliver |DF| = 2·|AB| = 2·5 = 10

Svar på opgave 4:

1. Den stamfunktion til f(x), der går gennem P(1,2) kaldes F(x) og findes ud fra det ubestemte integrale til f(x), som er x³ + 3x² + k. (Her er benyttet reglen om integration af potensfunktioner og reglen om integration af summer.)

   Man sætter F(x) = x³ + 3x² + k og skal bestemme k, så F(1) = 2. Det giver: F(1) = 1³ + 3·1² + k = 2 ⇒ k = -2.

   Dermed bliver stamfunktionen F(x) = x³ + 3x² - 2

Svar på opgave 5:

1. Tangentens ligning er: y = f´(x₀)·(x - x₀) + f(x₀).

   Her er x₀ = 2 og f(x₀) = 7. f´(x₀) = f´(2) findes ved hjælp af højresiden i differentialligningen: f'(2) = [(7 - 1)/2] = 3.

   Man får at tangentens ligning er: y = f´(2)·(x - 2) + 7 ⇒ y = 3·(x - 2) + 7 ⇒ y = 3x + 1

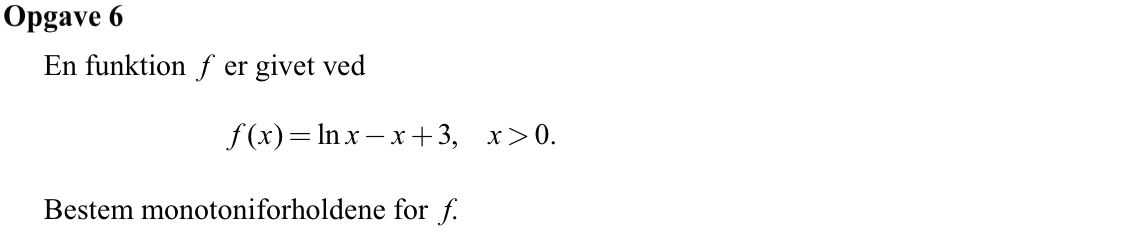
Svar på opgave 6:

1. Man skal finde nulpunkterne for f´(x) og lave en fortegnsundersøgelse.

   f´(x) = (1/x) - 1, x > 0.

   Nulpunkterne for f´(x) findes: f´(x) = 0 ⇒ (1/x) - 1 = 0 ⇒ x = 1.

   Man får ved indsættelse af x = 0,5 og x = 1,5:

   f´(0,5) = 2 - 1 = 1 > 0 og f´(1,5) = (1/2) - 1 = -1/2 < 0.

   Dette giver følgende monotoniforhold for f: f er voksende for x < 1 og aftagende for x > 1

Svar på opgave 7:

1. For at opstille cirklens ligning skal man kende centrum og radius. Cirklens centrum = (-1,4). Radius = |CP| = √[(2 - (-1))² + (8 - 4)²] = √[25] = 5.

   Dvs. cirklens ligning er: (x - (-1))² + (y - 4)² = 5² = (x + 1)² + (y - 4)² = 5²

2. For at finde skæringspunkterne indsætter man x = -3 + t og y = 15 + 7t i cirklens ligning. Derved får man en ligning i t, som løses i Ti-Nspire:

   solve((−3+t+1)²+(15+7*t-4)²=5²,t) ▸ t=−2 or t=−1

   Ved at indsætte de to fundne t-værdier i linjens ligning, får man skæringspunkterne:

   (x,y) = (-3,15) + (-2)·(1,7) = (-5,1) og (x,y) = (-3,15) + (-1)·(1,7) = (-4,8)

Svar på opgave 8:

1. For at løse opgaven i Ti-Nspire skal man oprette to lister med rå data. Man kender ikke de rå data for kvinders blodtryk, men man kan nemt lave en liste af data med samme kvartilsæt ved simpelthen at dubblere medianen i kvartilsættet for kvinder. Dvs. man opretter listerne:

   kvinder:={115,117,120,120,122,128} ▸ {115,117,120,120,122,128}

   mænd:={119,129,120,121,122,129,122,127,123,119,120,123,127,128,129,120,121,123,127,129} ▸ {119,129,120,121,122,129,122,127,123,119,120,123,127,128,129,120,121,123,127,129}

   Disse lister giver boksplottene:

   

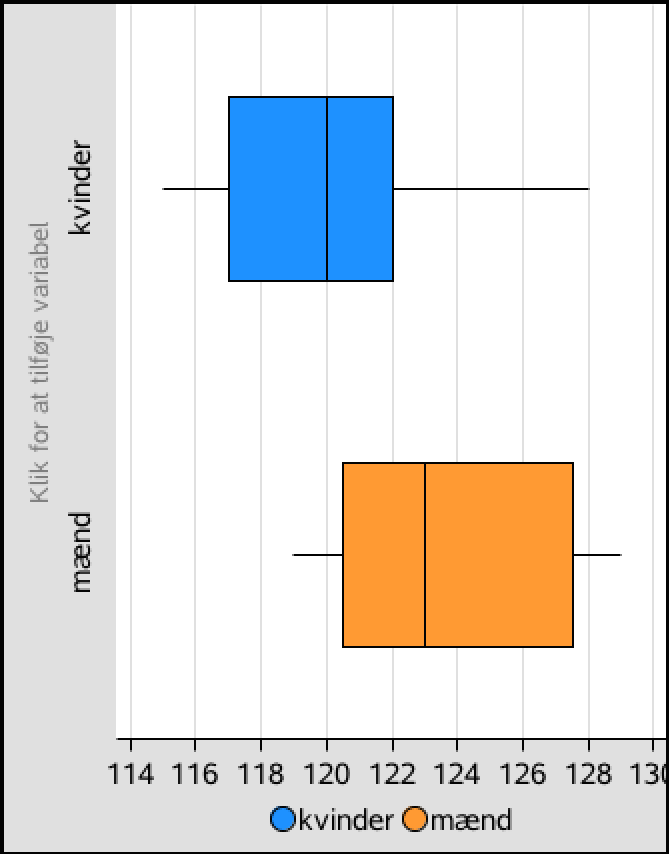
2. Det ses af boksplottene, at kvinder generelt har lavere blodtryk end mænd. Medianen er det blodtryk, som halvdelen af kvinderne henholdsvis mændene ligger under.

Svar på opgave 9:

1. Man opretter lister for vægt og stofkifte i Ti-Nspire:

   vægt:={0.3,2.4,6.4,13,29.3,51.8,59.6} ▸ {0.3,2.4,6.4,13,29.3,51.8,59.6}

   stofskifte:={28,135,293,520,956,1394,1591} ▸ {28,135,293,520,956,1394,1591}

   Man laver en potensregression på listerne i Ti-Nspire:

   PowerReg vægt,stofskifte,1: CopyVar stat.RegEqn,f1: stat.results ▸

   [["Titel","Potensregression"]
     ["RegEqn","a*x^b"]
     ["a",70.512]
     ["b",0.764626]
     ["r²",0.999713]
     ["r",0.999856]
     ["Resid","{...}"]
     ["ResidTrans","{...}"]]

   (Kommandoen findes under Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Potensregression...)

   Det ses at a = 0,765 og b = 70,51 (Ti-Nspire bytter som på a og b i forhold til opgaven.)

2. Man skal finde f(20). Den findes i Ti-Nspire til:

   f1(20) ▸ 696.729

   (f1 er en funktion, der automatisk oprettes ved regressionen. Se: "...CopyVar stat.RegEqn,f1: stat.results...")

   Dvs. stofskiftet for et dyr, der vejer 20 kg er 697 kcal/døgn

3. Den procentvise ændring findes ved formlen:

   ((1+15%)^0,765 - 1)·100 % = 11,28 %

   Dvs. hvilestofskiftet for et dyr stiger med 11,3 %, når dyrets vægt stiger med 15 %.

Svar på opgave 10:

1. Tegnet i Geogebra:

   

   Man finder |AB| ved hjælp af en cosinusrelation. Dette er gjort i Ti-Nspire med følgende kommando:

   solve(cos(48*1.°)=(x²+13²-10²)/(2*x*13),x) ▸ x=6.11658 or x=11.2808

   Her vælger man den mindste værdi, da det er den, som gør vinkel B spids.

   Dvs. |AB| = 6,12

2. Arealet af BDC er 0,5·h_b·|DC| = 9, hvor h_b er højden fra b til B. h_b = |AB|·sin(48°) = 6,11658·sin(48°). Dette giver, at |DC| kan findes med følgende solve-kommando:

   solve((1/2)*6.11658*sin(48*1.°)*x=9,x) ▸ x=3.95996

   Det giver at |DC| = 3,96

Svar på opgave 11:

1. Tallet 60,297·10⁹ er mængden af tons CO₂ som blev udledt i 1950.

   Tallet 1,031 er fremskrivningsfaktoren, dvs. det tal som sidste års udledning skal ganges med for at få udledningen for det nye år.

2. Man opretter P(t), N(t) og P_N(t) = P(t)/N(t) i Ti-Nspire:

   p(t):=60.297*10⁶*(1.031)^t ▸ Udført

   n(t):=6.72*10⁷*t+2.594*10⁹ ▸ Udført

   p_n(t):=p(t)/n(t) ▸ Udført

   Forskriften for p(t)/n(t) findes:

   p_n(t) ▸ 0.8973*(1.031)^t)/(t+38.601)

   Modellen for den årlige udledning af CO₂ pr. person er derfor: 0.8973*(1.031)^t)/(t+38.601), hvor udledningen måles i tons og t er antal år efter 1950.

   Man bruger følgende kommando for at finde udledningen i 2012:

   p_n(2012-1950) ▸ 0.0592

   Den gennemsnitlige CO₂ udledning pr. person i 2012 bliver derfor i følge modellen: 0,0592 tons/person/år = 59,2 kg/person/år

Svar på opgave 12:

1. Man opretter punkterne som stedvektorer i Ti-Nspire:

   a:=[7,3,0] ▸ [7,3,0]

   b:[1,1,6] ▸ [1,1,6]

   c:=[−5,13,0] ▸ [−5,13,0]

   d:=[1,8,0] ▸ [1,8,0]

   e:=[4,2,3] ▸ [4,2,3]

   f:=[−1,5,4] ▸ [−1,5,4]

   Man finder normalvektoren, n, til planen α som krydsproduktet af stedvektor d og stedvektor e:

   n:=crossP(d,e) ▸ [24,−3,−30]

   (Man kan bruge stedvektorer her, da planen går gennem (0,0,0)).

   Man opretter et tilfældigt punkt P = (x,y,z) i rummet:

   p:=[x,y,z] ▸ [x,y,z]

   For at P skal ligge i planen α skal der gælde at OP·n = 0. Dette bruges til at finde planens ligning:

   dotP(n,p)=0 ▸ 24*x-3*y-30*z=0

   Ligningen for α er derfor: 24x - 3y - 30z = 0, som forkortet med 3 giver: 8x - y - 10z = 0

2. Da O=(0,0,0) indgår i planen, der indeholder ODE kan afstanden mellem F og planen α findes som |OF·n|/|n|. Man får:

   abs(dotP(f,n)/norm(n))*1. ▸ 4.126

   Dvs. afstanden mellem F og α er 4,126

3. Man finder vinklen mellem planen α og planen β som vinklen mellem deres normalvektorer. Normalvektoren til β kaldes m og aflæses af koefficienterne til planens ligning som m = (5,6,7). Dette oprettes i Ti-Nspire:

   m:=[5,6,7] ▸ [5,6,7]

   Vinklen mellem n og m findes ved hjælp af følgende kommando:

   solve(cos(x*1.°)=dotP(n,m)/(norm(n)*norm(m)),x)|0≤x≤180 ▸ x=105.50

   Dvs. at den stumpe vinkel mellem α og β er 105,5°

Svar på opgave 13:

1. Man opretter f(x) i TI-Nspire:

   f(x):=1+0.1*x² ▸ Udført

   Tangenten gennem (5,f(5)) findes ved kommanden:

   y = tangentLine(f(x),x,5) ▸ y=x-1.5

   Dvs tangentens ligning er y = x - 1,5

2. Førstekoordinaten til tangenten skæringspunkt med x-aksen findes som løsning til ligningen: y = x - 1,5 = 0 ⇒ x = 1,5

   Rumfanget af leret i skålen findes ved hjælp af formlen for rumfanget af et legeme, der drejes 360° om x-aksen. Her skal man først finde omdrejningslegemet for f mellem x = 0 og x = 5 og derfra trække omdrejningslegemet for tangenten mellem x = 1,5 og x = 5. Man får:

   Integral(π*(f(x))²,x,0,5)-Integral(π*(x-1.5)²,x,1.5,5) ▸ 16.624

   Dermed er skålens lerrumfang 16,6

Svar på opgave 14:

1. Man løser differentialligningen i Ti-Nspire:

   deSolve(v'-(1/(15-t))*v=300/(15-t)-9.81 and v(0)=0,t,v) ▸ v=−4.905*t*(t+31.1621)/(t-15.)

   Forskriften for v er v(t) = −4.905·t·(t + 31,162)/(t - 15)

   Tidspunktet, hvor farten er oppe på 1000 m/s, findes med kommandoen:

   solve(−4.905*t*(t+31.1621)/(t-15.)=1000,t)|0≤t≤14 ▸ t=12.361

   Dvs. raketten opnår farten 1000 m/s efter 12,4 sekunder

Svar på opgave 15:

1. Kilen rumfang er 0,5·h·x². Da dette skal være 100 cm³ får man: 0,5·h·x² = 100 ⇒ h = 200/x².

   Kilens over flade betår af bunden med arealet x², to trekantede sideflader med arealet 2·(0,5·h·x) = h·x, en bagside med arealet x·h og en skrå flade med arealet x·√(x² + h²). Dette giver til sammen :

   Overflade: x² + h·x + x·h + x·√(x² + h²) = x² + 2·h·x + x·√(x² + h²). Heri indsættes h = 200/x² og man får:

   O(x) = x² + 2·(200/x²)·x + x·√(x² + (200/x²)²) = x·√(x² + 40.000/x⁴) + x² + 400/x

2. For at finde mindsteværdien for O(x) oprettes funktionen i Ti-Nspire:

   o(x):=x*sqrt(x²+40000/x⁴)+x²+400/x ▸ Udført

   Det x, der giver mindsteværdien, findes med kommandoen:

   fMin(o(x),x)|0≤x≤10 ▸ x=5.520

   Det x, der giver det mindste overfladeareal er derfor: x = 5,52 cm