

Svar på opgave 1:
-
Modellen er positiv lineær, da der sker en konstant årlig tilvækst. Modellen kan skrives:
f(x) = ax + b, hvor x = antal år efter 2004, f(x) er årligt el-forbrug til fjernsyn, a er den årlige tilvækst på 82 GWh og b er startværdien på 765 GWh.

Svar på opgave 2:
-
Ligningen for tangenten i (2,f(2)) er y = f´(2)·(x - 2) + f(2).
Her er f(x) = 3x2 - 4x + 8 og f´(x) = 6x - 4. Dette giver f(2) = 3·22 - 4·2 + 8 = 12 og f´(2) = 6·2 - 4 = 8. Dette indsættes og man finder ligningen:
y = 8·(x - 2) + 12 ⇒ y = 8x - 4
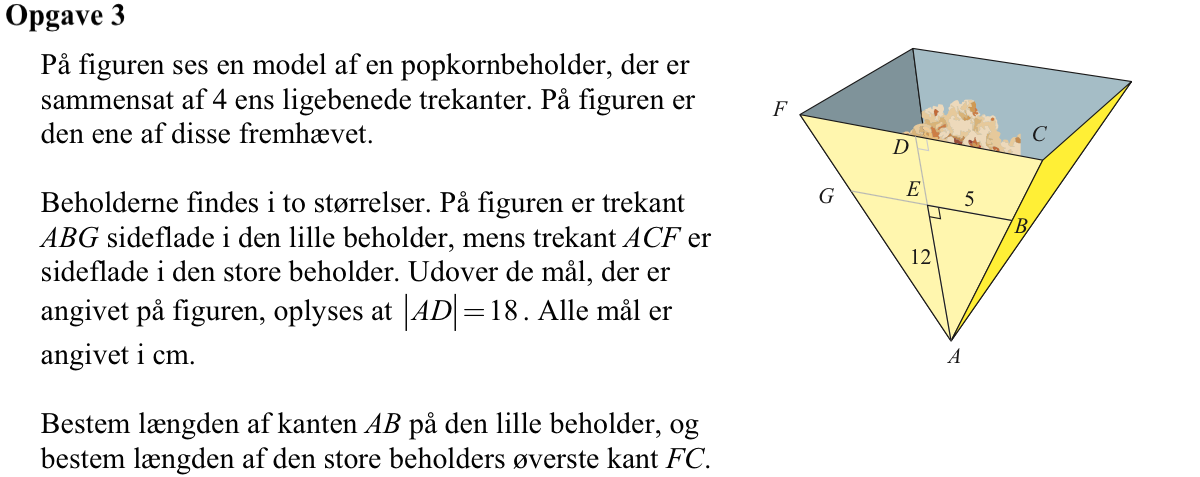
Svar på opgave 3:
-
|AB| findes ved hjælp af Pythagoras læresætning: |AB| = √[122 + 52] cm = √196 cm = 13 cm
Trekanterne ABG og ACF er ensvinklede. Deres skaleringsfaktor er |AD|/|AE| = 18/12 = 3/2. Dermed er |FC| = (3/2)·|GB| cm = (3/2)·(2·|EB|) cm = 3·|EB| cm = 3·5 cm = 15 cm

Svar på opgave 4:
-
For at finde cirklens radius og centrum, skal man omskrive den til formen (x-a)2 + (y-b)2 = r2, hvor r er radius og (a,b) er centrum.
Omskrivningen foregår ved at lave en kvadratkomplettering med hensyn til x og y:
For x får man: x2 + 2x = x2 + 2x + (2/2)2 - (2/2)2 = (x2 + 2x + 1) - 1 = (x+1)2 - 1
For y får man: y2 - 4y = y2 - 4y + (4/2)2 - (4/2)2 = (y2 - 4y + 4) - 4 = (y-2)2 - 4
Dette indsætte i den oprindelige ligning: x2 + 2x + y2 - 4y = 4 ⇒ (x+1)2 - 1 + (y-2)2 - 4 = 4 ⇒ (x+1)2 + (y-2)2 = 9 ⇒ (x+1)2 + (y-2)2 = 32.
Heraf ses at centrum er (x,y) = (-1,2) og radius er 3

Svar på opgave 5:
-
Man integrerer ved hjælp af substitution, idet det bemærkes, at tælleren i brøken er lig med nævneren differentieret.
Man sætter u = 2x2 + 3 og får du/dx = 4x ⇒ du = 4x·dx.
Dette giver med u og du indsat: ∫[4x/(2x2+3)] dx = ∫[4x·dx/(2x2+3)] = ∫[du/u] = ∫(1/u) du = ln(|u|) = ln(|2x2 + 3|) = ln(2x2 + 3) (det bemærkes, at 2x2 + 3 altid er større end 0).

Svar på opgave 6:
-
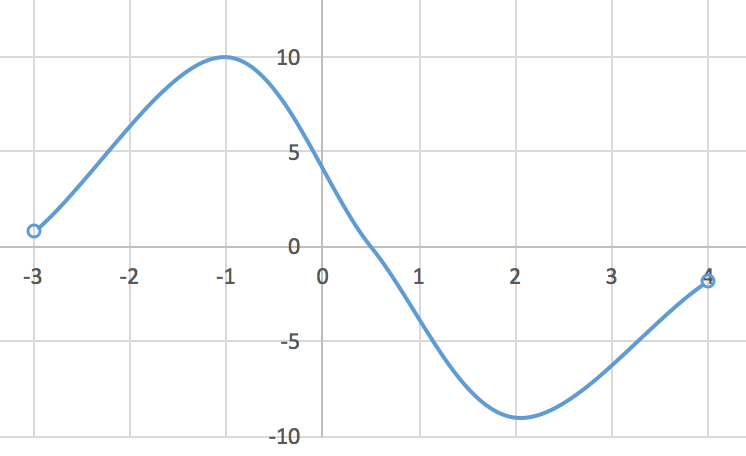
Nedenstående tegning er lavet i Excel.
Det ses af oplysningerne i opgaven, at f(x) har maksimum i x = -1 (f´(x) er positiv før x = -1 og negativ efter) og minimum i x = 2 (f´(x) er negativ før x = 2 og positiv efter).


Svar på opgave 7:
-
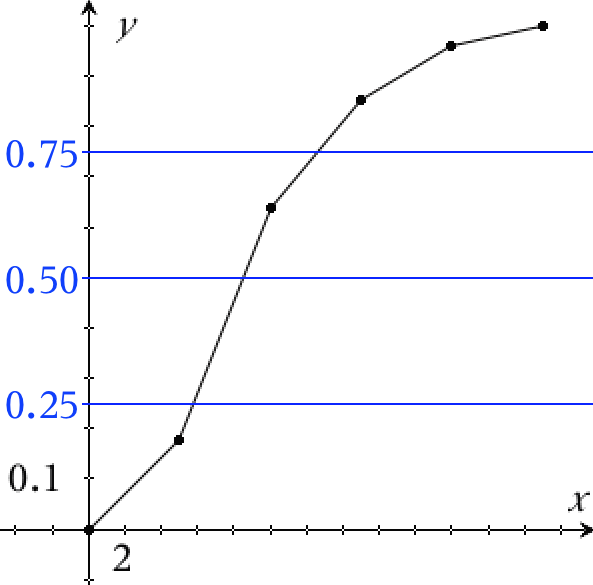
Sumkurven tegnet i Ti-Nspire. x = antal elever og y = procentvis fravær.
Sumkurven bygger på følgende lister, som er oprettet i Ti-Nspire:
fravær:={0,5,10,15,20,25} ▸ {0,5,10,15,20,25}
elever:={0,101,262,122,63,22} ▸ {0,101,262,122,63,22}
Man tilføjer 0 til starten af hver liste. Dette 0 er dels nedre grænse i første fraværs-interval, dels antallet af elever under denne grænse.
Ud fra den sidste liste laves listen over kummulerede frekvenser af antal elever
frekvenssum:=cumulativeSum(elever/sum(elever))*1.) ▸ {0,0.177,0.637,0.851,0.961,1.}
-
Kvartilsættes aflæses ud fra skæringspunkterne mellem sumkurven og de blå linjer på ovenstående figur. De blå linjer repræsenterer de summerede frekvenser: 25 %, 50 % og 75 %. Man aflæses x-værdierne for hvert skæringspunkt og får kvartilsættet:
nedre kvartil = 5,8% fravær, median = 8,5% fravær og øvre kvartil = 12,6% fravær
For at finde andelen af elever, som har mere end 12 %'s fravær, tegner man en lodret linje gennem 12 % på x-aksen af sumkurven.
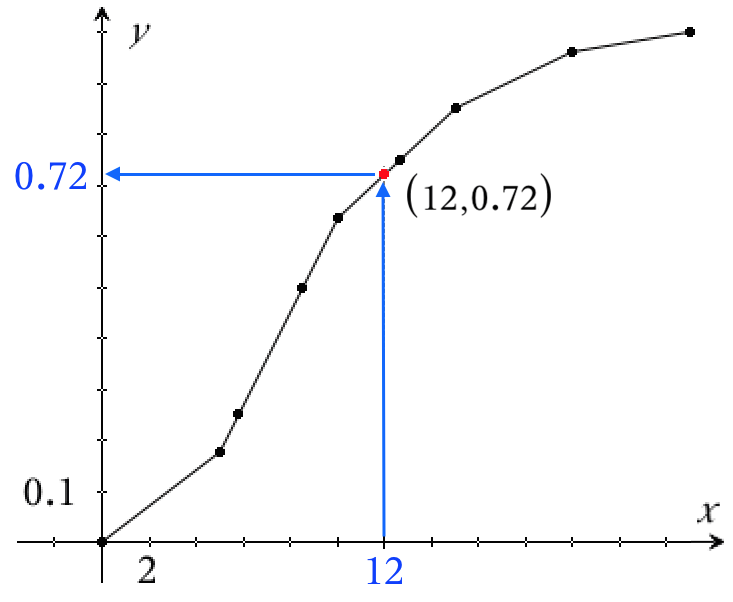
Det ses at linjen skærer sumkurven i 0,722 = 72 % (skæring vist med rød prik, koordinater vist i parentes). Dvs. at 72 % af eleverne har 12 % fravær eller mindre, hvilket igen vil sige, at
procentdelen af elever som har mere end 12 %'s fravær er 100 % - 72 % = 28 %

Svar på opgave 8:
-
Man finder vinkel A i Ti-Nspire ved hjælp af en cosinusrealtion:
solve(cos(x*1.°)=(12.52+102-172)/(2*12.5*10),x)|0<x<180 ▸ x=97.527
Dvs. vinkel A er 97,5°
-
Man finder |CD| ved hjælp af en sinusrelation i Ti-Nspire:
solve(sin(18.5°)/3.5=sin(64°)/x),x) ▸ x=9.9141
Dvs. |CD| = 9,91
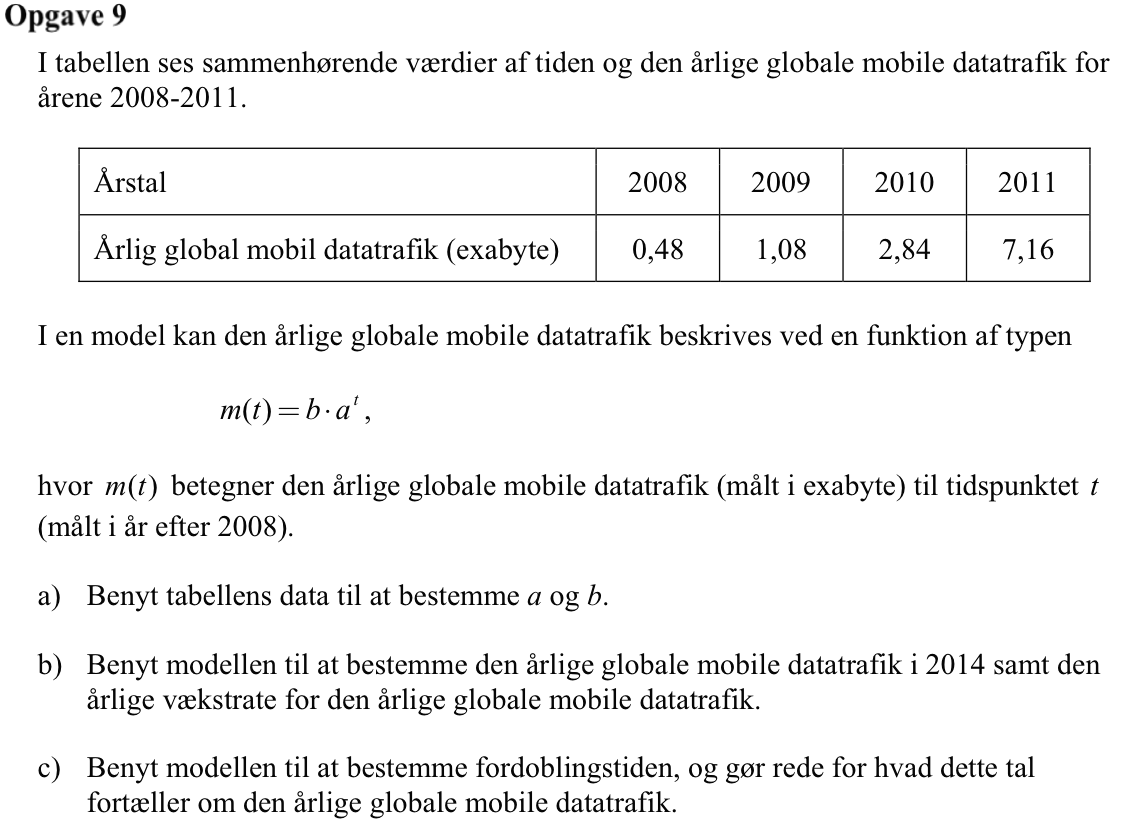
Svar på opgave 9:
-
Man opretter lister med årstal og datatrafik i Ti-Nspire:
årstal:={2008,2009,2010,2011}-2008 ▸ {0,1,2,3}
datatrafik:={0.48,1.08,2.84,7.16} ▸ {0.48,1.08,2.84,7.16}
Dette bruges til at lave en eksponentiel regression med følgende kommando i Ti-Nspire:
ExpReg årstal,datatrafik,1: CopyVar stat.RegEqn,f1: stat.results ▸

Bemærk at Ti-Nspire bruger a og b modsat opgaven. Man får derfor: a = 2,4779 og b = 0,4619
-
Den årlige datatrafik i 2014 er i følge modellen:
f1(2014-2008) ▸ 106.938
(f1(x) = 0,4619·2,4779x oprettes automatisk, bemærk: "...f1: stat.results")
Dvs. datatrafikken forventes at blive 106,9 exabyte i 2014
Den årlige vækstrate er a - 1 = 2,4779 - 1 = 1,478
-
Fordoblingstiden er: ln(2)/ln(2.47794) år = 0,764 år
Dette viser at datatrafikken mere end fordobles hvert år.

Svar på opgave 10:
-
Vinklen mellem fladerne findes som vinklen mellem normalvektorerne til de planer som fladerne ligger i. Da man ved, at vinklen er spids, så trækkes den fra 180°, hvis den er over 90°.
Først oprettes punkterne A-E som stedvektorer i Ti-Nspire:
a:=[80,−50,125] ▸ [80,−50,125]
b:=[0,0,150] ▸ [0,0,150]
c:=[0,300,150] ▸ [0,300,150]
d:=[80,350,125] ▸ [80,350,125]
e:=[0,300,0] ▸ [0,300,0]
Normalvektoren til den plan, som fladen OAB ligger i har krydsproduktet af vektorerne OA og OB. Dette gøres i Ti-Nspire med kommandoen:
n:=crossP(a,b) ▸ [−7500,−12000,0]
Man dividerer denne vektor med største fælles divisor, som findes i Ti-Nspire
gcd(7500,12000) ▸ 1500
...og får derefter en normalvektor, n, som består af små hele tal.
n:=n/1500 ▸ [−5,−8,0]
En normalvektor til frontfladen kaldes m. Denne vektors koordinater aflæses af koefficienterne til ligningen for det plan som frontfladen ligger i: -25x + 0y + 16z = 0. Dette indsættes i Ti-Nspire:
m:=[−25,0,16] ▸ [−25,0,16]
Man finder vinklen mellem n og m med følgende kommando:
solve(cos(x*1.°)=dotP(n,m)/(norm(n)*norm(m)),x)|0<x<180 ▸ x=63.4869
Dvs. vinklen mellem planerne er 63,5°
-
Fladen OADE dele op i to trekanter: OAD og ODE og man bruger formlen for arealet af en trekant i rummet, der siger at det er halvdelen af krydsproduktet af de to trekanter der udspænder trekanten:
(1./2)*norm(crossP(a,d))+(1/2)*norm(crossP(d,e)) ▸ 51942.9
Dvs. arealet af firkanten OADE er 51942,9 cm2 = 5,194 m2
-
Man opretter linjens parameterfremstilling som en funktion i Ti-Nspire:
l(t):=[16*t,60*t,150-25*t] ▸ Udført
Man indsætter x = 16t, y = 60t og z = 150 - 25t i ligningen for planen, der indeholder frontfladen, og løser den medhensyn til t:
solve(−25*16*t+16*(150-25*t)=0,t) ▸ t=3
Dette t indsættes i linjens parameterfremstilling for at få skæringspunktet mellem plan og linje:
l(3) ▸ [48,180,75]
Dvs. skæringspunktet mellem den centrale del af lysstrålen og frontfladen er (48,180,75)
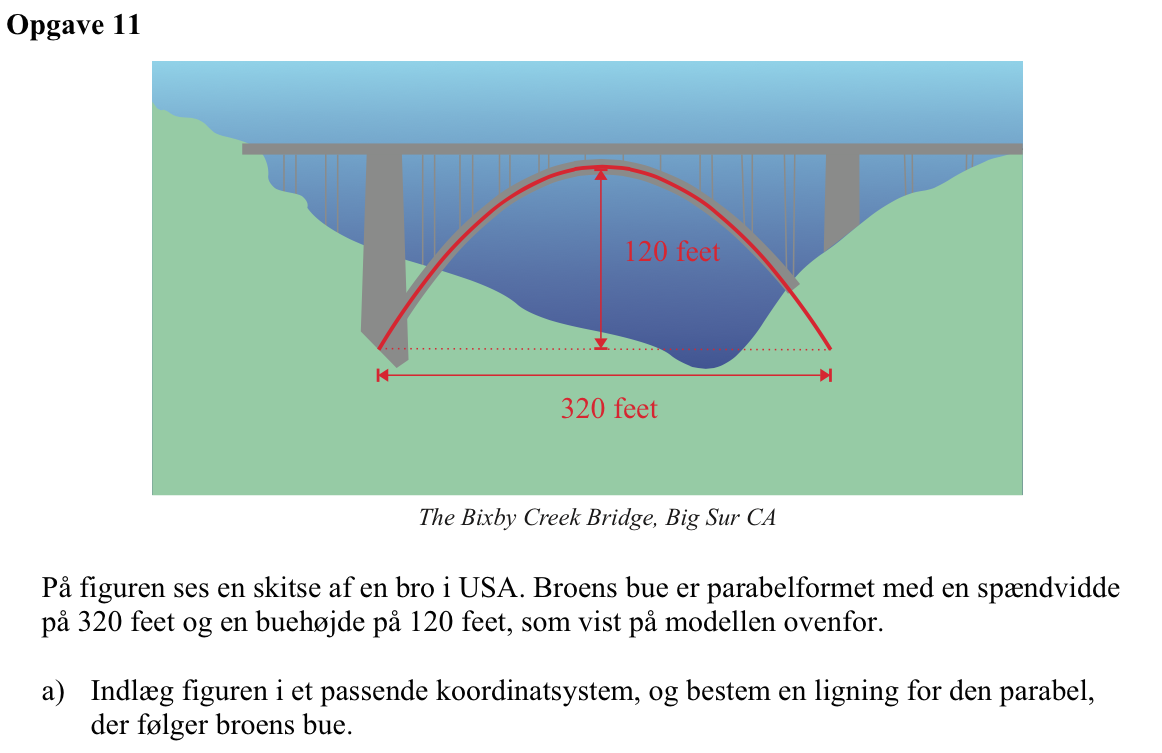
Svar på opgave 11:
-
Parablen har ligningen y = a·x2 + bx + c. Man vælger det koordinatsystem, der har den punkterede linje som x-akse og parablens symmetriakse som y-akse. I dette koordinatsystem bliver b = 0, fordi parablens toppunkt ligger på y-aksen og c = 120 m, da det er parablens skæring med y-aksen.
Man ved at parablen skærer x-aksen for x = 320/2 = 160, a·x2 + bx + c = 0 for x = 160. Man finder a ved at indsætte x = 320/2, b = 0 og c = 120 i parablens ligningen, sætte den lig med 0 og løse med hensyn til a:
solve(a*(320/2)2+120=0.,a) ▸ a=−0.0046875
Dette giver a = −0,00469, som indsat i parablens ligning giver: y = −0,00469·x2 + 160

Svar på opgave 12:
-
Funktionen for deceleration oprettes i Ti-Nspire:
f(t):=16400/((t-68)2+400)+1480/((t-93)2+18) ▸ Udført
Grafen tegnes i Ti-Nspire:
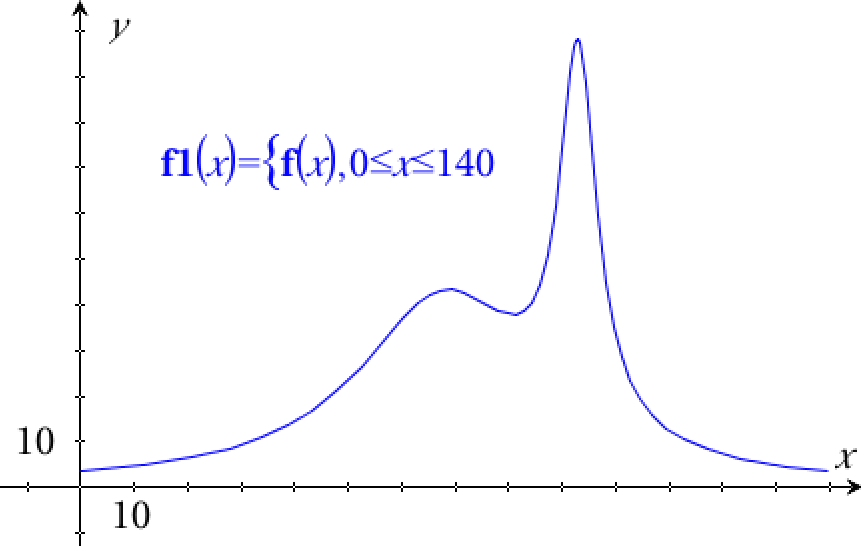
Der t, der giver maksimumværdien, findes med kommandoen
fMax(f(t),t) ▸ t=92.914
Denne værdi indsaættes i f(t) og man får maksimumværdien:
f(92.9141) ▸ 98.256
Dvs. den største deceleration, som dukken udsættes for, er 98,26 m/s2
-
SI findes i Ti-Nspire med kommandoen:
Integral((f(t))2.5,t,0,140) ▸ 982847.7
Dvs. SI = 982.848
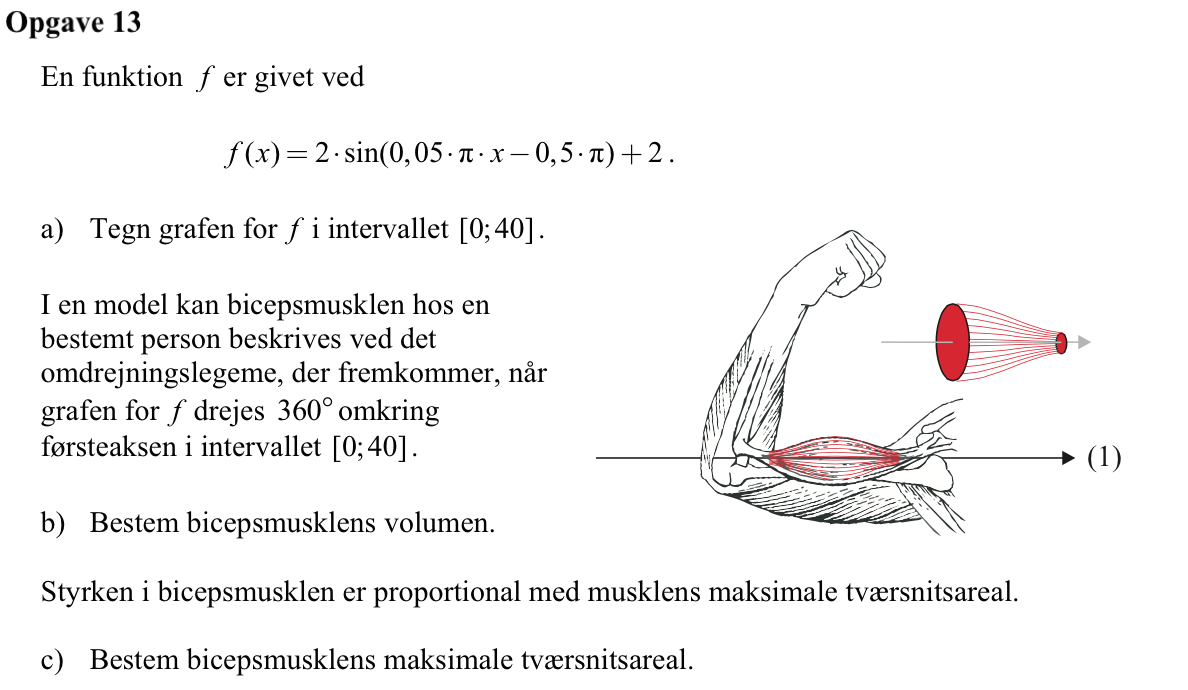
Svar på opgave 13:
-
Funktion oprettet og tegnet i Ti-Nspire:
f(x):=2*sin(0.05*π*x-0.5*π)+2 ▸ Udført
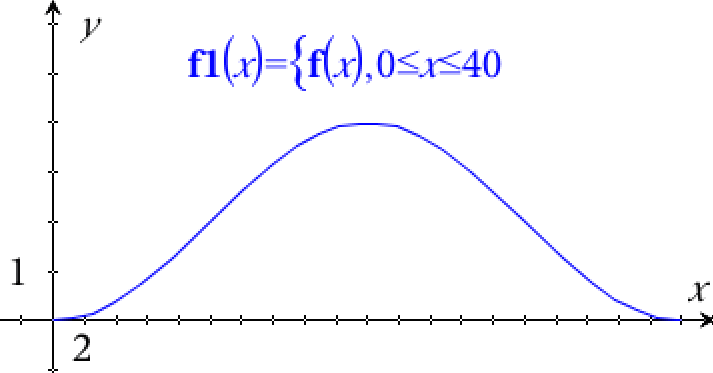
-
Man bruger formlen for rumfanget af et omdrejningslegeme ved rotation om x-aksen. Det giver i Ti-Nspire:
Integral(π*(f(x))2,x,0,40) ▸ 753.982
Dvs. rumfanget er 754,0
-
Tværsnittet er en cirkel. Det maksimale tværsnitsareal findes ved x = 20, der ligger midt på sinuskurven. Radius her er f(20). Det giver følgende areal beregnet i Ti-Nspire:
π*(f(20))2 ▸ 50.265
Dvs. det maksimale tværsnitsareal er 50,3
Svar på opgave 14:
-
Væksthastigheden findes ved at indsætte k = 3300 og m = 85 på højre side i differentialligningen (når dm/dt er isoleret på venstre side). Det giver følgende i Ti-Nspire:
3300/7000-(42/7000)*85. ▸ −0.03857
Dermed er væksthastigheden −0,0386 kg/døgn, dvs. vægten aftager med 0,0386 kg/døgn
-
Man løser differentialligningen med hensyn til m(t) i Ti-Nspire:
deSolve(m'=k/7000-(42/7000)*m and m(0)=87.,t,m) ▸ m=(87.-0.02381*k)*(0.9940)t+0.02381*k
Dvs. m(t) = (87 - 0,02381·k)·0,9940t + 0,02381·k
-
Man løser ligningen (87 - 0,02381·k)·0,9940100 + 0,02381·k = 80 med hensyn til k i Ti-Nspire
solve((87-0.02381*k)*(0.9940)100+0.02381*k=80,k) ▸ k=3002.3
Dvs. k = 3002 for en person, der vejer 80 kg efter 100 døgn.