Svar på opgave 1:

1. (p+q)² - (p² - q²) - 2·p·q =

   p² + 2·p·q + q² - p² + q² - 2·p·q =

   p² + q² - p² + q² =

   2·q²

Svar på opgave 2:

1. x² + x - 30 = 0 ⇔

   x = -(1/2) ±(1/2)√[1+4·30] ⇔

   x = -(1/2) ±(1/2)√[121] ⇔

   x = -(1/2) ±(1/2)·11 ⇔

   x = -(1/2) - (1/2)·11 ∨ x = -(1/2) + (1/2)·11 ⇔

   x = -12/2 ∨ x = 10/2 ⇔

   x = -6 ∨ x = 5

Svar på opgave 3:

1. Arealet af parallelogrammet er den numeriske værdi af determinanten til de to vektorer. Determinanten til a og b kan også skrives som skalarproduktet af tværvektoren til a = (a^) = (-2,3) og b = (-2,5). Dvs.

   |det(a,b)| = |(a^)·b| = (-2,3)·(-2,5) = 19.

   Dvs. arealet af parallelogrammet er 19

Svar på opgave 4:

1. Man skal undersøge hvilken af de tre funktioner f₁, f₂ eller f₃, der er lig med F'. Man får:

   F'(x) = 6x⁵·e^x + x⁶·e^x. Dette er lig med f₂(x).

   Dermed er F stamfunktion til f₂

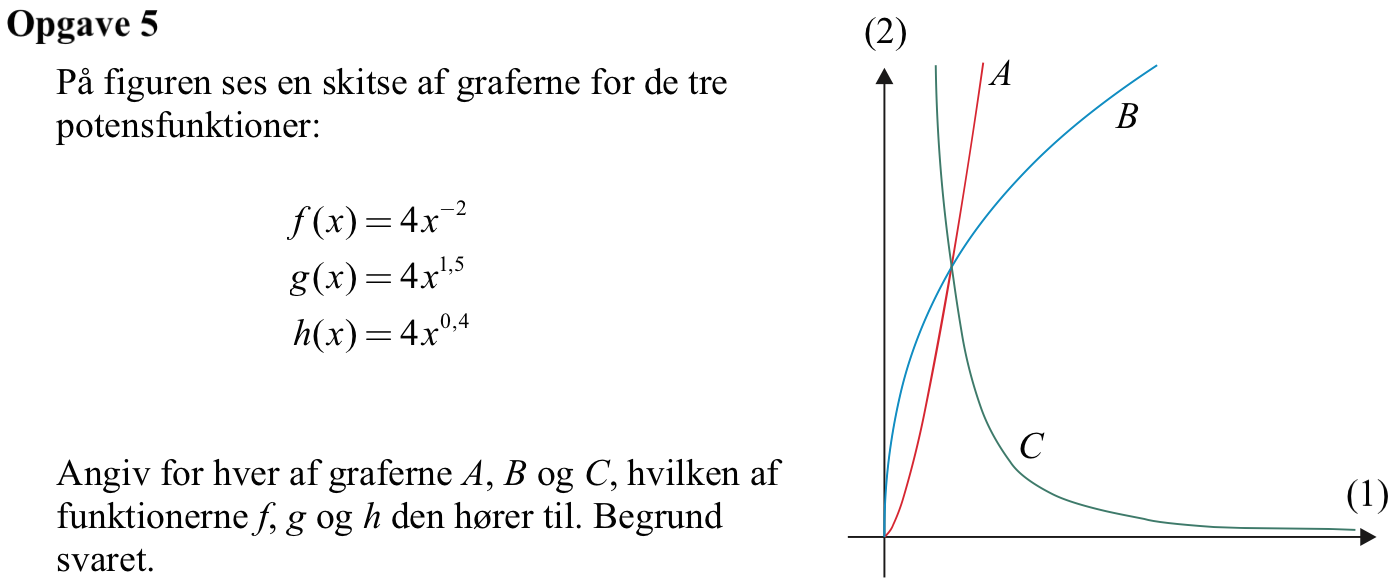
Svar på opgave 5:

1. Man kan sige noget om størrelsen af eksponenten a ud fra graferne.

   A vokser hurtigere og hurtigere, dermed er a > 1.

   B vokser langsommere og langsommere, dermed er 0 < a < 1.

   C aftager, dermed a < 0.

   Dvs. A er graf til g, B er graf til h og C er graf til f

   (De skærer i øvrigt hinanden i punktet (1,4), hvilket ses ved at sætte x = 1 ind i hver af funktionsforskrifterne.)

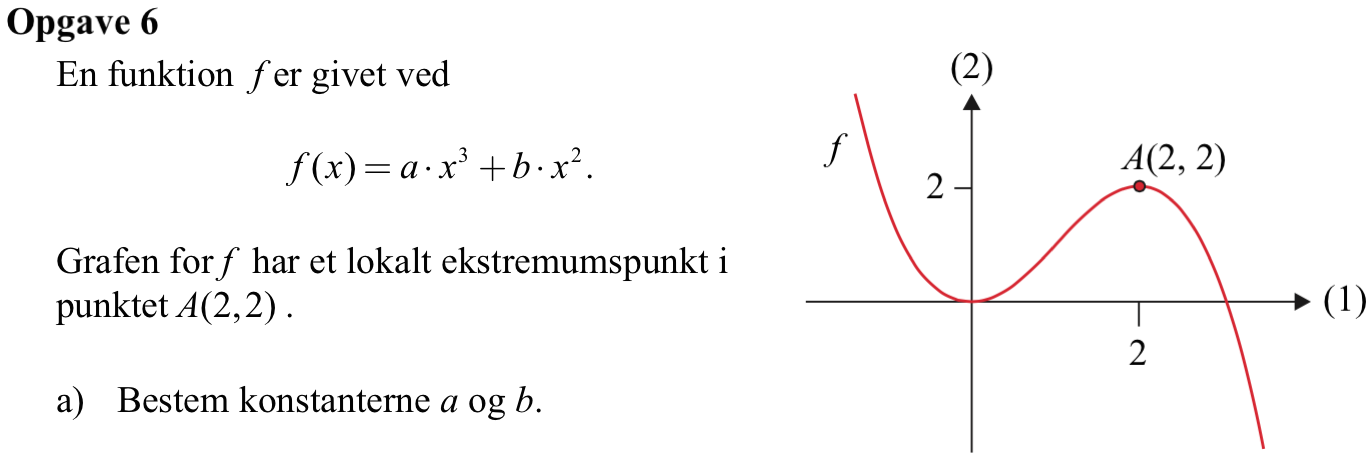
Svar på opgave 6:

1. Oplysningen A = (2,2) ligger på grafen for f betyder, at f(2) = 2 eller a·2³ + b·2² = 2 ⇒ 8a + 4b = 2 ⇒ 4a + 2b = 1.

   Oplysningen A = (2,2) er ekstremumspunkt på grafen for f betyder, at f´(2) = 0 eller 3·a·2² + 2·b·2 = 0 ⇒ a = -(1/3)·b.

   Ved at indsætte a = -(1/3)·b i den første ligning får man 4·(-1/3)b + 2b = 1 ⇒ [(-4/3) + 2]·b = 1 ⇒ (2/3)·b = 1 ⇒ b = 3/2.

   Dvs. a = -(1/3)·(3/2) = -1/2 og b = 3/2

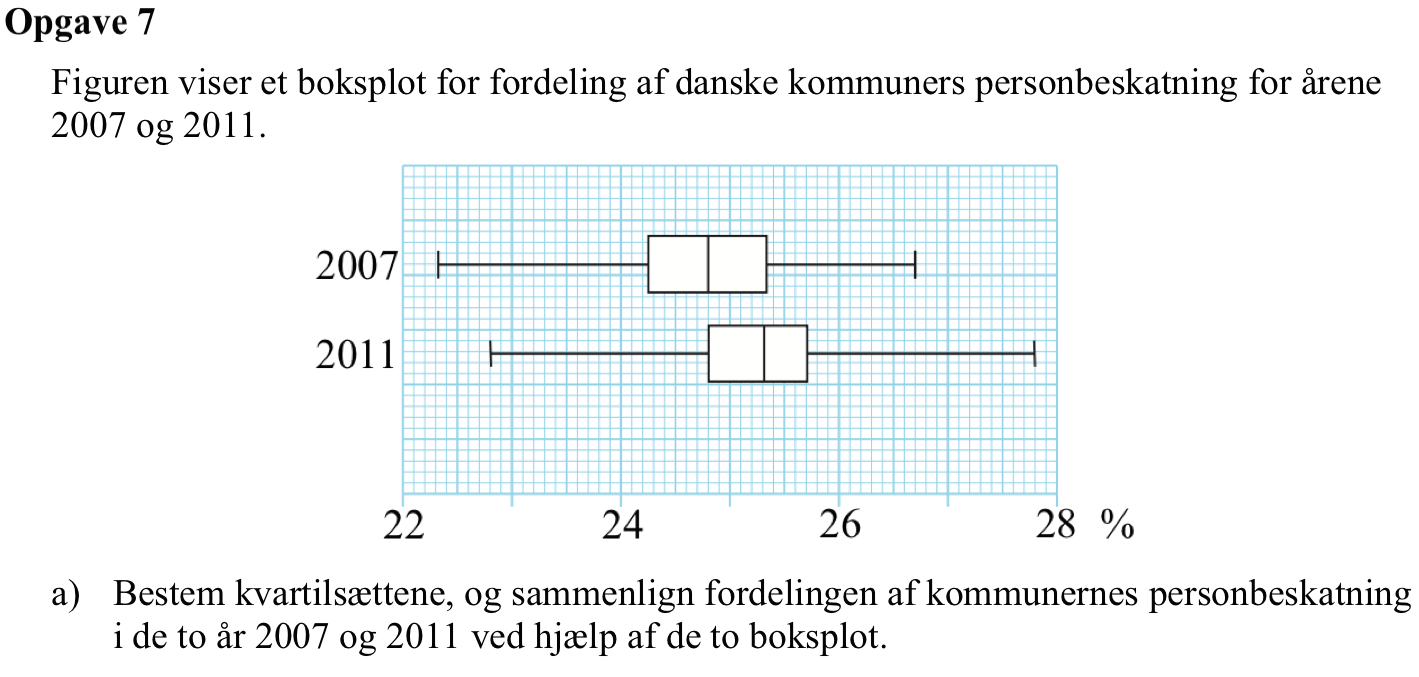
Svar på opgave 7:

1. Kvartilsæt:

   2007: nedre kvartil = 24,2 %, median = 24,8 % og øvre kvartil = 25,3 %

   2011: nedre kvartil = 24,8 %, median = 25,3 % og øvre kvartil = 25,7 %

   Generelt ligger beskatningsprocenterne højere i 2011 end i 2007. Medianen er større og variationsbredden omtrent den samme.

Svar på opgave 8:

1. Man opretter y(x) = ax + b.

   y(x):=a*x+b ▸ Udført

   Man man løser ligningerne y(1) = 1 og y(5) = 3:

   solve(y(1)=1 and y(5)=3,a,b) ▸ a=1/2 and b=1/2

   Dette giver ligningen y = 0,5·x + 0,5 eller x - 2·y + 1 = 0

2. Parablens toppunkt er (x_T,y_T) = ([-b/(2a)],[-d/(4a)]) = (-(-8)/2;-(8²-4·13,5)/4) = (4;-2,5)

   Afstanden mellem toppunktet til parablen og linje findes ved hjælp af distanceformlen:

   Afstand = |4·1-(-2,5)·(-2) + 1|/√[1² + 2²] = |4 + 5 + 1|/√[5] = 10/√[5] = 4,472

3. Toppunktets projektion på linjen l er skæringspunktet mellem l og en linje gennem toppunktet vinkelret på l.

   

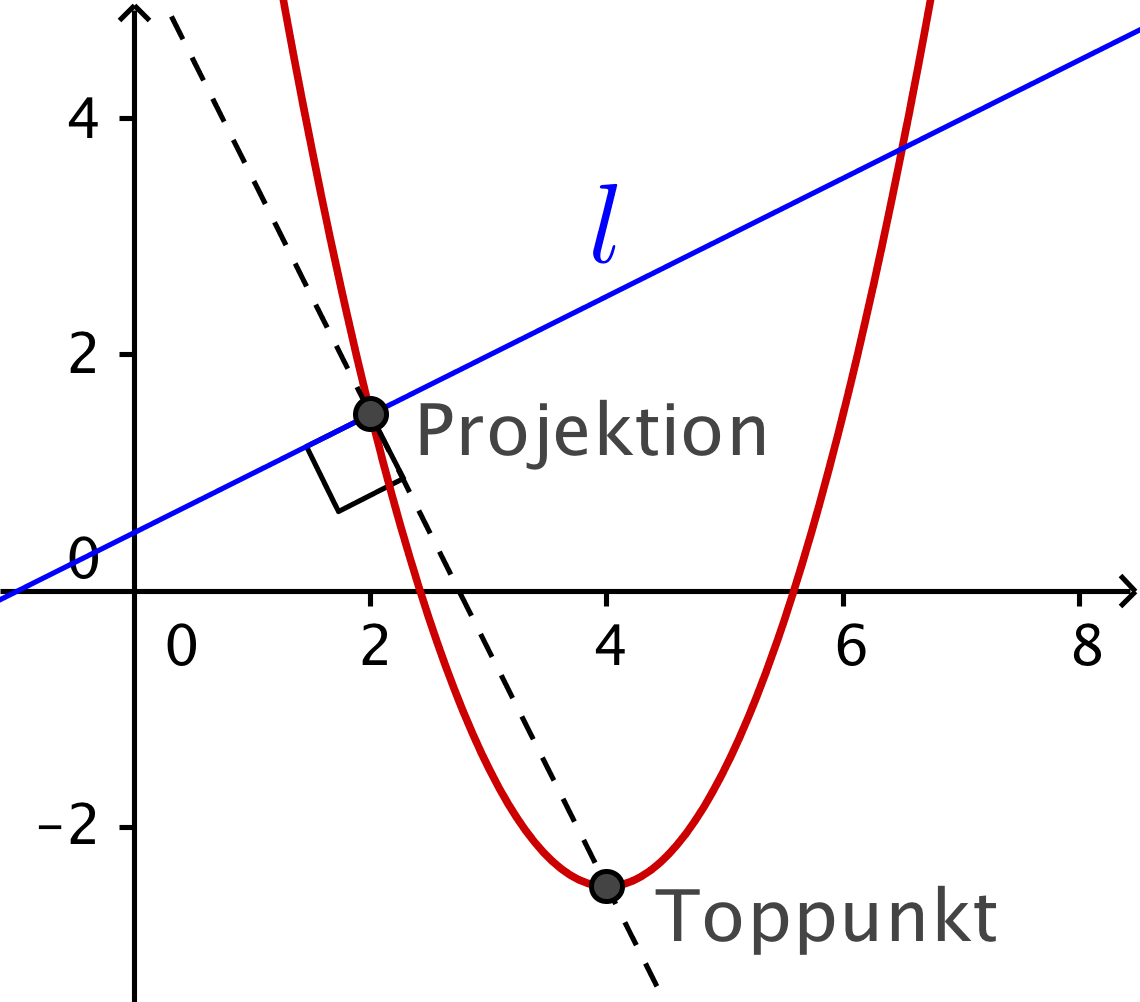
   Ligningen for den vinkelrette linje er y = -1/(0,5)·x + c = -2x + c, hvor c findes ved at indsætte toppunktet (4;-2,5):

   -2,5 = -2·4 + c ⇒ c = -2,5 + 8 = 5,5

   Man skal finde skæringspunktet mellem linjerne y = 0,5x + 0,5 og y = -2x + 5,5. Deres skæringspunkt findes i Ti-Nspire:

   solve(y=0.5*x+0.5 and y=−2*x+5.5,x,y) ▸ x=2. and y=1.5

   Dvs. projektionen er (x,y) = (2;1,5)

Svar på opgave 9:

1. Man finder ∠ACB ved hjælp af en cosinusrelation

   solve(cos(x*1.°)=(12.8²+28²-22.4²)/(2*12.8*28),x)|0<x<180 ▸ x=51.514

   Dvs. ∠ACB = 51,5°

   Nedenfor er trekanten med højden i B (H_B) indtegnet.

   

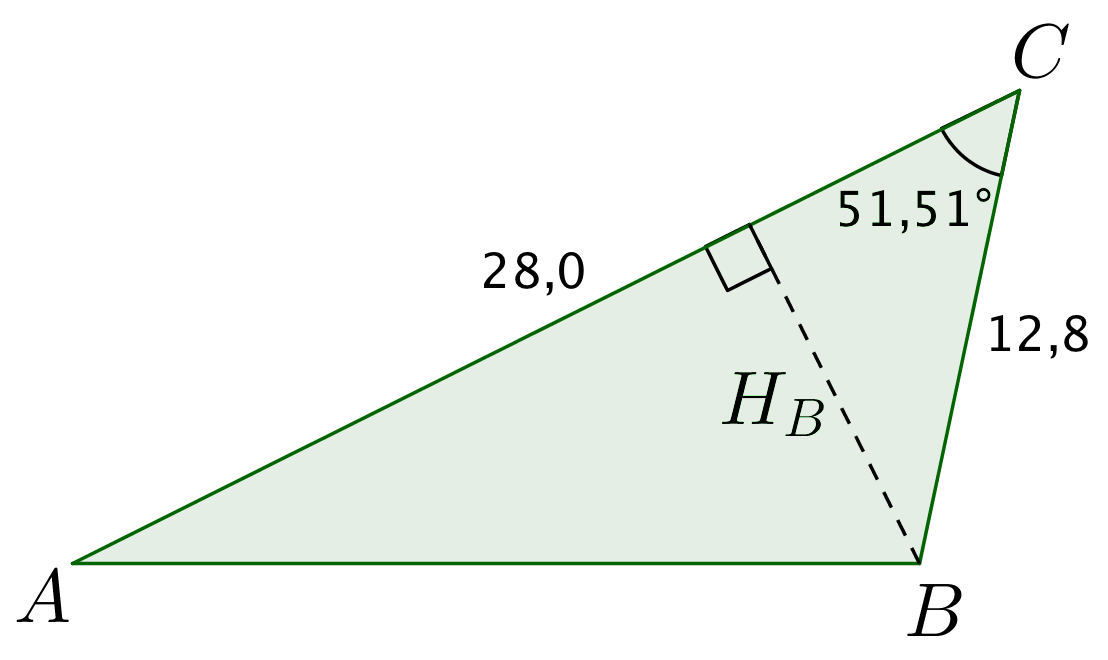
   Arealet er 0,5·|AC|·H_B = 0,5·|AC|·|BC|·sin(∠ACB) = 0,5·28·12,8·sin(51.514°) = 140,3

2. Nedenfor er trekanten med punkterne D og E tegnet.

   

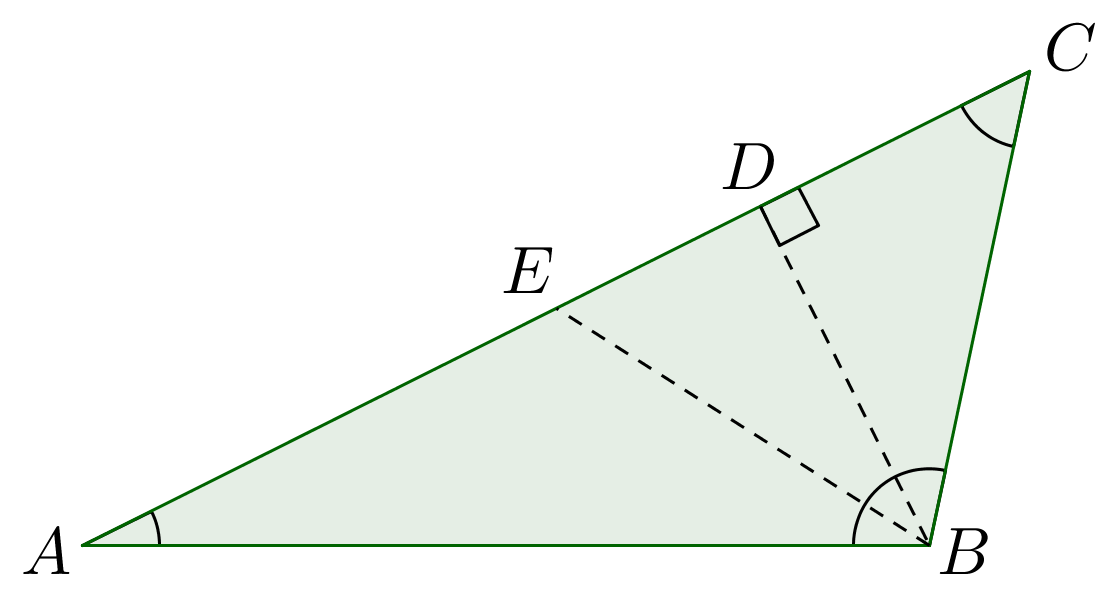
   Man ved, at |CE| er 0,5·|AC| = 14.

   Man ved også, at |CD| = |BC|·cos(∠C) = 12,8·cos(51,514°) = 7,966

   Dvs. |DE| = |CE| - |CD| = 14 - 7,966 = 6,03

Svar på opgave 10:

1. Man opretter en liste for masserne:

   masse:={0.025,0.314,3.5,11.4} ▸ {0.025,0.314,3.5,11.4}

   ...og en liste for hastigheder:

   hastighed:={72.85,529.4,2751,7079.4} ▸ {72.85,529.4,2751,7079.4}

   Man laver potensregression på de to lister med kommandoen:

   Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Potensregression...

   Det giver...

   PowerReg masse,hastighed,1: CopyVar stat.RegEqn,f1: stat.results ▸

   

   Heraf ses at a = 0,7395 og b = 1153,8

   Man kan også bruge kommandoen f1(x), der er den regressionsfunktion som Ti-Nspire opretter (se ovenfor: "PowerReg...stat.RegEqn,f1:..."):

   f1(x) ▸ 1153.8·x^0.7395

2. Man skal bestemme v(70), som gøres i Ti-Nspire med regressions-funktionen:

   f1(70) ▸ 26707.43

   Dvs. hastigheden hvormed blodplasmaet renses i et dyr, der vejer 70 kg. er 26707 mL/h

   Man skal bestemme x så v(x) = 5000. Det gøres i Ti-Nspire med solve-kommandoen:

   solve(f1(x)=5000,x) ▸ x=7.2634

   Dvs. dyrets vægt er 7,263 kg, når blodplasmaet renses med en hastighed af 5000 mL/h.

3. Der menes nok "den procentvise ændring". Den er:

   (1.2^0.7395-1)*100 ▸ 14.434

   Dvs. den procentvise ændring i hastigheden ved en 20 % ændring af dyrets vægt er 14,4 %

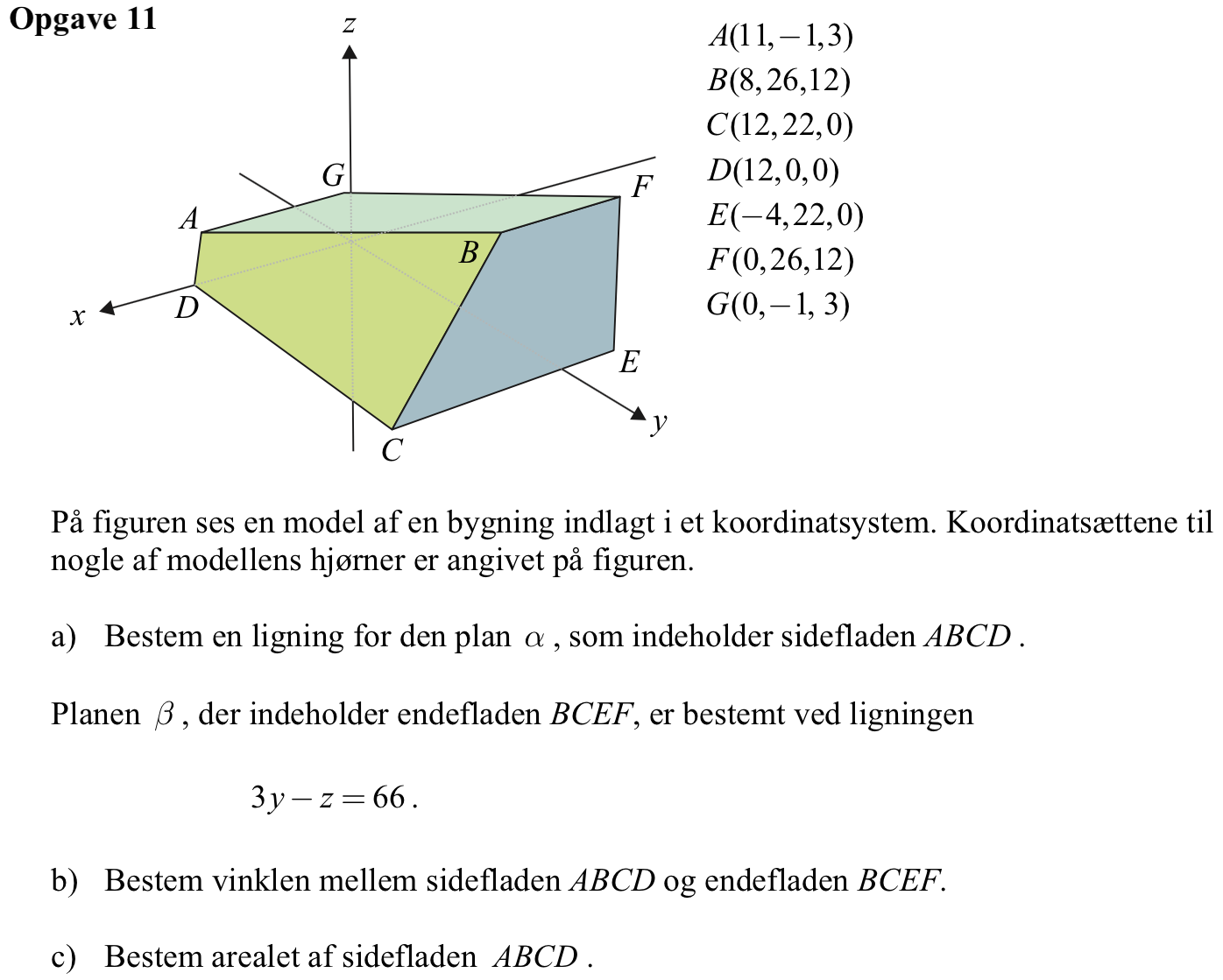
Svar på opgave 11:

1. Først opretter man punkterne A-D i Ti-Nspire som stedvektorer

   a:=[11,−1,3] ▸ [11,−1,3]

   b:=[8,26,12] ▸ [8,26,12]

   c:=[12,22,0] ▸ [12,22,0]

   d:=[12,0,0] ▸ [12,0,0]

   Man opretter derefter vektorerne AB og AD

   ab:=b-a ▸ [−3,27,9]

   ad:=d-a ▸ [1,1,−3]

   Man beregner krydsproduktet af AB og AD:

   crossP(ab,ad) ▸ [−90,0,−30]

   Normalvektoren, n, til planen α defineres ud fra krydsproduktet af AB og AD.

   n:=[−90,0,−30] ▸ [−90,0,−30]

   Der oprettes nu vektoren AX, som er en vektor fra A til et vilkårligt punkt (x,y,z) i planen α:

   ax:=[x,y,z]-a ▸ [x-11,y+1,z-3]

   Der gælder at skalarproduktet (eller prikproduktet) mellem n og AX er lig med nul. Dette benyttes til at finde planens ligning:

   dotP(n,ax)=0 ▸ −90*x-30*z+1080=0

   Dvs. en ligning for planen α er -90x - 30z + 1080 = 0. For at få små hele tal med færrest mulige minustegn, divideres igennem med -30, så den endelige ligning bliver:

   3x + z - 36 = 0

2. Man beregner vinklen mellem planerne α og β ved hjælp af deres normalvektorer.

   En normalvektor, m, til β aflæses af β's ligning: 3y - z = 66 ⇒ 0x + 3y + (-1)z = 66.

   Dvs. m = (0,3,-1). Denne vektor oprettes i Ti-Nspire:

   m:=[0,3,−1] ▸ [0,3,−1]

   Man indsætter nu n og m i formlen for vinklen mellem to planer og får:

   solve(cos(x*1.°)=dotP(n,m)/(norm(n)*norm(m)),x)|0<x<180 ▸ x=84.2608

   Dvs. vinklen mellem α og β er enten 84,26° eller 180° - 84,26° = 95,74°

   Ud fra en tegning i geogebra ser man at den spidse vinkel er den rigtige.

   Vinklen mellem væggene er dermed 84,26°

Nedenstående tegning viser planerne α og β med væggene ABCD og BCEF. Vinklen mellem de to firkanter er angivet. Desuden er arealet af firkant ABCD vist.



3. For at finde arealet af firkant ABCD inddeles den i to trekanter: trekant ADB og trekant BCD.

   Man opretter vektorerne cd og bc

   bc:=c-b ▸ [4,−4,−12]

   cd:=d-c ▸ [0,−22,0]

   Man benytter, at arealet af en trekant i rummet er halvdelen af krydsproduktet af to vektorer, der udspænder den. Man får:

   0.5*norm(crossP(ab,ad))+0.5*norm(crossP(cd,bc)) ▸ 186.574

   Dvs. arealet af firkant ABCD er 186,6

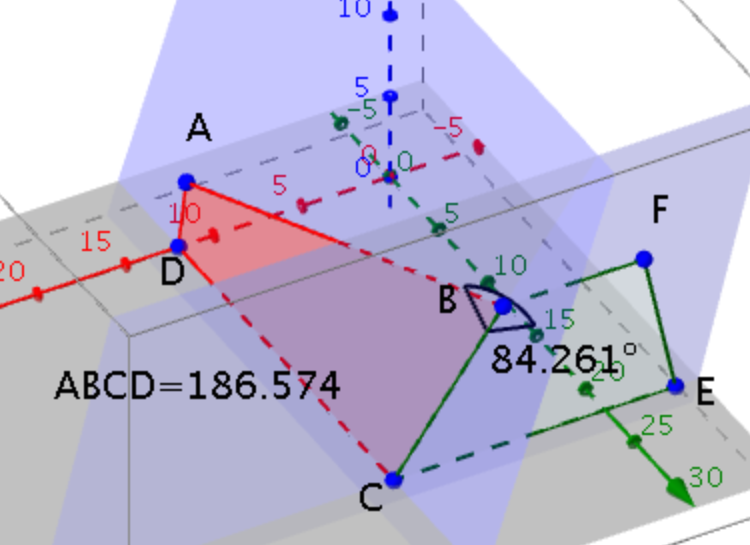
Svar på opgave 12:

1. Man løser differentialligningen ved hjæp af desolve-kommandoen i Ti-Nspire:

   deSolve(s'=1.5-(2/(100+t))*s and s(0)=30,t,s) ▸ s=0.5*(t³+300.*t²+30000.*t+600000.)/(t+100.)²

   Man forenkler formlen:

   expand(0.5*(t³+300*t²+30000*t+600000)/(t+100)²) ▸ −200000./(t+100)²+0.5*t+50.

   Dvs. løsningen er S(t) = 0,5·t + 50 − 200.000/(t + 100)²

2. S(t) oprettes i Ti-Nspire:

   s(t):=0,5·t+50−200.000/(t+100)² ▸ Udført

   solve(s(t)=60,t) ▸ t=40.316

   Dvs. saltmængden i karret er 60 kg efter 40,3 min.

Svar på opgave 13:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=6.5*sin(0.0849*x)+6 ▸ Udført

   Arealet af M er integralet af f(x) fra x = 0 til x = 38. Det beregnes i Ti-Nspire:

   integral(f(x),x,0,38.) ▸ 380.847

   Dvs. arealet af M er 380,8 cm²

   Nedenunder er M (gråt) og grafen for f (grøn streg) tegnet i Geogebra. Arealet af M er også vist beregnet i Geogebra.

   

2. Man indsætter formlen for O(x) i Ti-Nspire:

   2*π*integral(f(x)*sqrt(1+(derivative(f(x),x))²),x,0,38) ▸ 2545.6

   Dvs. overfladearealet er 2545,6 cm²

Svar på opgave 14:

1. Volumen = (2·r)²·h + (1/2)·(4π/3)·r³ = 2πr³/3 + 4hr

2. Man man findes h udtryk ved r i volumenformlen, idet volumenet skal være 5. Man bruger solve-kommandoen i Ti-Nspire:

   solve((2*π*r³/3)+4*h*r²=5,h) ▸ h=−(2*π*r³-15)/(12*r²)

   Dette udtryk for h indsættes i formlen for overfladearealet:

   (π+8)*r²+8*h*r|h=(−(2*π*r³-15)/(12*r²) ▸ −((π-24)*r³-30)/(3*r)

   Dette omskrives ved hjælp af expand-kommandoen:

   expand(−((π-24)*r³-30)/(3*r) ▸ ((−π*r²)/3)+8*r²+(10/r)

   Dvs. overfladearealet er (−πr²)/3 + 8r² + 10/r = 10/r + (8 − π/3)·r²

3. Man indsætter en numerisk værdi for π i formlen for overfladearealet og bruger fMin-kommandoen til at finde mindsteværdien af O(r) for r mellem nul og 50.

   (−π*1.*r²)/3)+8*r²+(10/r) ▸ 6.9528*r²+(10/r)

   fMin(6.9528*r²+(10/r),r)|0<r<50 ▸ r=0.8959

   Dvs. den radius, der giver det mindste overfladeareal for en dåse med rumfanget 5 er 0,896