Svar på opgave 1:

1. (a - b)² + 2a·(a + b) - b² =

   a² - 2ab + b² + 2a² + 2ab - b² =

   1a² + 2a² - 2ab + 2ab + 1b² - 1b² =

   1a² + 2a² + (-2)·ab + 2ab + 1b² + (-1)·b² =

   (1 + 2)·a² + ((-2) + 2)·ab + (1 + (-1))·b² =

   3a² + 0ab + 0b² =

   3a²

Svar på opgave 2:

1. Man skal finde t, så skalarproduktet af vektor a og vektor b giver 0. Man får:

   (2,t)·(-3,4) = 0 ⇔

   2·(-3) + t·4 = 0 ⇔

   -6 + t·4 = 0 ⇔

   t·4 = 6 ⇔

   t = 6/4 = 3/2

Svar på opgave 3:

1. Man omskriver kuglens ligning til normalform: (x-a)²+(y-b)²+(z-c)²=r² for at kunne aflæse centrum og radius.

   Dette gøres ved hjælp af kvadratkomplettering af den givne ligning med hensyn til x, y og z:

   x² - 2x + y² + 6y + z² + 2z + 2 = 0 ⇔

   (x² - 2x + (2/2)²) - (2/2)² + (y² + 6y + (6/2)²) - (6/2)² + (z² + 2z + (2/2)²) - (2/2)² + 2 = 0 ⇔

   (x - (2/2))² - (2/2)² + (y + (6/2))² - (6/2)² + (z + (2/2))² - (2/2)² + 2 = 0 ⇔

   (x - 1)² - 1 + (y + 3)² - 9 + (z + 1)² - 1 + 2 = 0 ⇔

   (x - 1)² + (y - (-3))² + (z - (-1))² = 3²

   Det ses heraf, at kuglens centrum = (1,-3,-1) og dens radius = 3

Svar på opgave 4:

1. Man skal løse de to sammenhørende ligninger:

   f(3) = 1 ∧ f(6) = 8 ⇒

   b·a³ = 1 ∧ b·a⁶ = 8 ⇔

   b = a^-3 ∧ a^-3·a⁶ = 8 ⇔

   b = a^-3 ∧ a^-3+6 = 8 ⇔

   b = a^-3 ∧ a³ = 8 ⇔

   b = a^-3 ∧ a = 8^1/3 ⇔

   b = 2^-3 ∧ a = 2 ⇔ a = 2 ∧ b = 1/8

Svar på opgave 5:

1. Parablens skæringspunkter med x-aksen findes ved at løse den tilhørende andengradsligning:

   x² - 2x - 8 = 0 ⇔

   x = -1±(1/2)·√[4 + 4·8] ⇔

   x = -1±(1/2)·√[36] ⇔

   x = -1±3 ⇔

   x = -1 - 3 ∨ -1 + 3 ⇔

   x = -4 ∨ x = 2

   Da y-værdien til at punkt på x-aksen er 0, får man følgende koordinater til parablens skæringspunkter med x-aksen:

   (x,y) = (-4,0) og (x,y) = (2,0)

Svar på opgave 6:

1. Man har: x²·h = 9 ⇔ h = 9/x² m

   Man indsætter udtrykket for h som funktion af x ved et rumfang på 9 m³ ind i formlen for overfladearealet:

   2hx + x² ∧ h = 9/x² ⇔ x²+18/x

Svar på opgave 7:

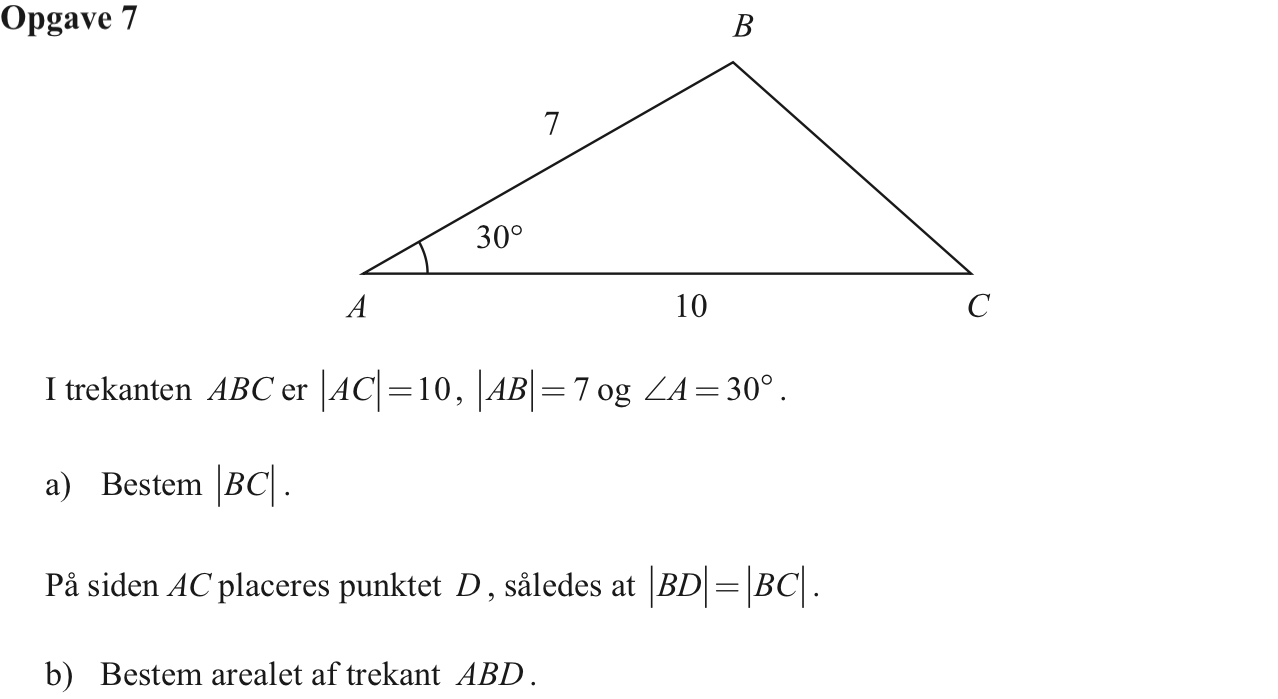
1. |BC| bestemmes ved hjælp af en cosinusrelation i Ti-Nspire:

   solve(cos(30.°)=(7²+10²-x²)/(2*7*10),x)|0<x ▸ x=5.26844

   Dvs. |BC| = 5,27

2. Arealet er 0,5·(højden i B)·|AD|. Højden i B = 7·sin(30°) = 3,50. Man mangler nu at finde AD, som er vist på figuren nedenunder.

   

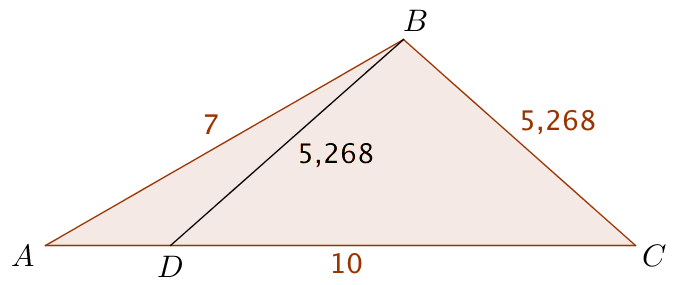
   Her bruger man igen en cosinusrelation. Den ubekendte er her den ene hosliggende side til vinkel A:

   solve(cos(30.°)=(7²+x²-5.268²)/(2*7*x),x)|0<x ▸ x=2.12435 or x=10.

   Da |AC| = 10, ses det, at |AD| = 2,124.

   Arealet giver: 0,5·(højden i B)·|AD| = 0,5·3,50·2,124 = 3,72

Svar på opgave 8:

1. Man opretter lister for x (liste_x) og f(x) (liste_y) i Ti-Nspire:

   liste_x:={20,40,60,80} ▸ {20,40,60,80}

   liste_y:={0.035,0.063,0.085,0.1} ▸ {0.035,0.063,0.085,0.1}

   Man vælger følgende kommando i Ti-Nspire: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Potensregression... hvorefter man vælger de to lister, som man lige har oprettet og får:

   PowerReg liste_x,liste_y,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Potensregression"]
   ["RegEqn","a*x^b"]
   ["a",0.003596]
   ["b",0.76693]
   ["r²",0.994664]
   ["r",0.997328]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Heraf ses at a = 0,7669 og b = 0,003596

   Det bemærkes at Ti-Nspire bruger a og b modsat opgaven. For en sikkerheds skyld kan man bruge kommandoen:

   f1(x) ▸ 0.003596·x^0.76693

   Dette er den regressionsfunktion, som Ti-Nspire selv opretter.

2. Kraftpåvirkningen er f(45), som findes i Ti-Nspire:

   f1(45) ▸ 0.066631

   Dvs. kraftpåvirkningen er 0,067 N

3. Man bruger formlen for procent-procent vækst i TI-Nspire:

   (1+30%)^0.76693-1)*100 ▸ 22.2888

   Dvs. kraftpåvirkningen vokser med 22,3 %

Svar på opgave 9:

1. Man opretter punkterne T, A, B og C i Ti-Nspire som vektorer:

   t:=[0,0,520] ▸ [0,0,520]

   a:=[400,0,200] ▸ [400,0,200]

   b:=[280,280,200] ▸ [280,280,200]

   c:=[0,400,200] ▸ [0,400,200]

   Man opretter herefter vektorene AT og AB, som ligger i planen α

   at:=t-a ▸ [−400,0,320]

   ab:=b-a ▸ [−120,280,0]

   En normalvektor, n, til α er lig med krydsproduktet af AT og AB:

   n:=crossP(at,ab) ▸ [−89600,−38400,−112000]

   Man opretter en vektor AX fra punktet A, der ligger i α til et vilkårligt punkt i rummet:

   ax:=[x,y,z]-a ▸ [x-400,y,z-200]

   De punker, der ligger i planen α opfylder, at skalarproduktet af AX og n = 0. Man får:

   dotP(n,ax)=0 ▸ −89600*x-38400*y-112000*z+58240000=0

   Dette kan forkortes med -3200, og man får den enklere ligninge for planen α:

   28x + 12y + 35z - 18200 = 0

2. Man bruger afstandsformlen for afstanden mellem punktet (0,0,0) og planen med ligningen 12x + 28y + 35z = 18200 i Ti-Nspire:

   abs(12*0+28*0+35*0-18200.)/√[12²+28²+35²] ▸ 392.238

   Dvs. afstanden mellem (0,0,0) og β er 392,2

3. Man finder vinklen mellem α og β som vinklen mellem planernes normalvektorer. Normalvektoren til β aflæses af planens ligning: 12x + 28y + 35z = 18200. Dvs. m = (12,28,35). Denne vektor oprettes i Ti-Nspire:

   m:=[12,28,35] ▸ [12,28,35]

   Man indsætter vektorerne n og m i formlen for vinklen mellem vektorer i Ti-Nspire:

   solve(cos(x*1.°)=dotP(n,m)/(norm(n)*norm(m)),x)|0<x<180 ▸ x=151.775

   Dvs. vinklen mellem α og β er enten 151,8° eller 180° - 151,8° = 28,2°.

   Ud fra billedet ses det, at vinklen er stump og dermed lig dermed 151,8°

Svar på opgave 10:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=x²-50*ln(x) ▸ Udført

   Man finder tangenten gennem (3,f(3)) med tangentLine-kommandoen (man kan sætte "y=" foran som vist her for at få vist ligningen med det samme)

   y=tangentLine(f(x),x,3.) ▸ y=−10.6667*x-13.9306

   Heraf ses, at tangentens ligning er y = −10,67x - 13,93

2. Man skal løse ulighederne f´(x)<0 og f´(x)>0. Det gøres i Ti-Nspire (idet x>0):

   solve(derivative(f(x),x)<0,x)|x>0 ▸ 0<x<5

   solve(derivative(f(x),x)>0,x)|x>0 ▸ x>5

   Dvs. f(x) aftager for 0 < x < 5 og vokser for x > 5

3. Man skal finde en ret linje gennem (0,0), der er tangnt til grafen for f.

   Først finder man det x, der opfylder ligningen: f´(x)·x = f(x). Dette gøres i Ti-Nspire:

   solve(derivative(f(x),x)*x=f(x),x) ▸ x=2.41824

   Dvs. tangentens ligning bliver y = f´(2.41824)·x ⇒ y = −15,8x

   Nedenunder er grafen for f tegnet med blåt og tangenten med rødt i Ti-Nspire.

   

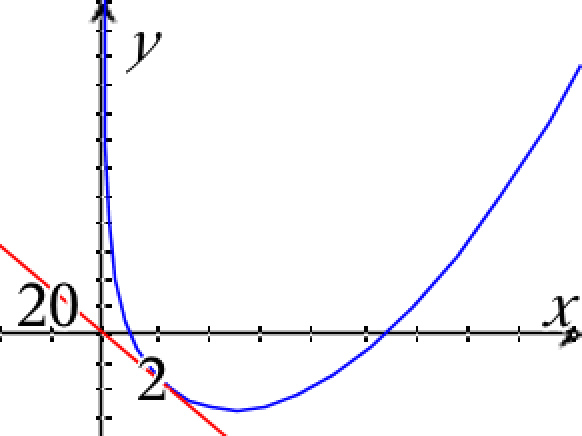
Svar på opgave 11:

1. Forskriften findes i TI-Nspire ved hjælp af desolve-kommandoen:

   deSolve(c'=0.4-0.02*c and c(0)=0,t,c) ▸ c=20.-20.*(0.980199)^t

   Dvs. C(t) = 20 - 20·0,9802^t

2. C(t) oprettes i Ti-Nspire:

   c(t):=20.-20.*(0.980199)^t ▸ Udført

   I Ti-Nspire tegner man nedenstående graf for f (blå streg) og y = 10 (rød streg).

   

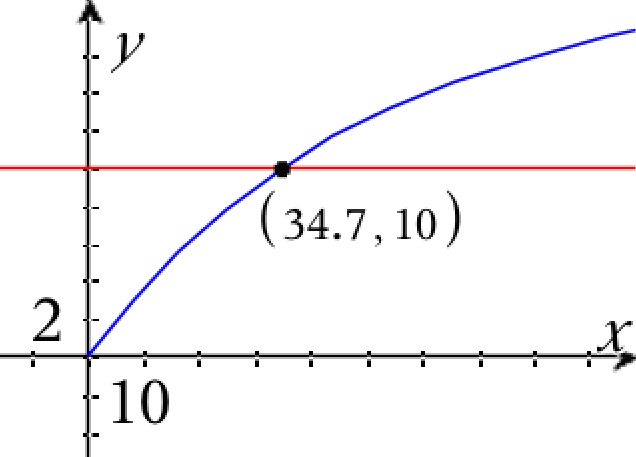
   Det tidspunkt hvor koncentrationen af forurenende stof er 10 ppm findes som skæringen mellem de to kurver.

   Tidspunktet kan også findes ved hjælp af solve-kommadnoen:

   solve(c(t)=10,t) ▸ t=34.6579

   Dvs. tidspunktet er t = 34,7 minutter

3. Man finder C'(15) i Ti-Nspire:

   derivative(c(t),t)|t=15 ▸ 0.296324

   Dvs. C'(15) = 0,296 ppm/minut

   Dette er ændringen i koncentrationen af forurenende stof pr. tidsenhed efter 15 minutter.

Svar på opgave 12:

1. Man opretter f(x) i TI-Nspire:

   f(x):=3*x+1/x ▸ Udført

   Arealet af M er integralet af 4 - f(x) mellem skæringspunkterne for f og y = 4. Skæringspunkternes x-værdier findes i Ti-Nspire:

   solve(f(x)=4,x) ▸ x=1/3 or x=1

   Dvs. man skal integrere mellem x = 1/3 og x = 1. Man får:

   ∫(4.-f(x),x,1/3,1) ▸ 0.234721

   Dvs. arealet af M er 0,235

2. Rumfanget findes med at trække rumfanget af omdrejningslegemet for y=4 mellem x = 1/3 og x = 1 fra rumfanget af omdrejningslegemet for f(x) mellem de samme værdier af x. Det giver i Ti-Nspire:

   π*(integral(4²,x,1/3,1)-integral(f(x)²,x,1/3,1.) ▸ 5.58505

   Dvs. rumfanget af omdrejningslegemet (som er en ring) er 5,585

Svar på opgave 13:

1. Man opretter f(x) i TI-Nspire:

   f(x):=211.4885-10.4801*(exp(0.0329*x)+exp(−0.0329*x)) ▸ Udført

   Buens bredde ved jordoverfladen er den numeriske værdi af differensen mellem f's nulpunkter. Nulpunkterne findes i Ti-Nspire:

   solve(f(x)=0,x) ▸ x=−91.2531 or x=91.2531

   Nulpunkterne er x=−91.2531 og x=91.2531. Dermed er bredden |−91.2531-91.2531| m = 182,5 m

2. Man sætter a = −91.2531 og b = 91.2531 i formlen i TI-Nspire og får:

   integral(sqrt(derivative(f(x),x)²)+1),x,−91.2531,91.2531) ▸ 451.255

   Dvs. buens længde er 451,3 m

Svar på opgave 14:

1. Hældningen er lig med 0,17·f(x). Man skal finde hælningen i P = (0,f(0)) = (0,3).

   Dvs. hældningen til kurven i P er 3·0,17 = 0,51

   Differentialligningen er y' = 0,17·y med begyndelsesbetingelsen: y(0)=3.