Svar på opgave 1:

1. Metode 1:

   Et andengradspolynomium y = ax² + bx + c har toppunktet: (x,y) = (-b/(2a),c-b²/(4a)).

   Her har man polynomiummet: y = 2x² − 8x + 3, dvs. a = 2, b = -8 og c = 3.

   Dvs. toppunkt = (-(-8)/(2·2),3 - (-8)²/(4·2)) = (2,-5)

   Metode 2:

   Grafen til et andengradspolynomium, P(x), har vandret tangent i toppunktet og dermed gælder, at P'(x) = 0 for x lig med toppunktets førstekoordinat.

   Her får man P'(x) = 0 ⇒ 4x - 8 = 0 ⇔ x = 2. Toppunktets andenkoordinat er følgelig: P(2) = 2·2² - 8·2 + 3 = -5.

   Dvs. toppunkt = (2,-5)

Svar på opgave 2:

1. Modellen er: f(x) = 499x + 250, hvor x er antallet af kubikmeter grus og f(x) er prisen for gruset i kroner.

Svar på opgave 3:

1. Man får:

   

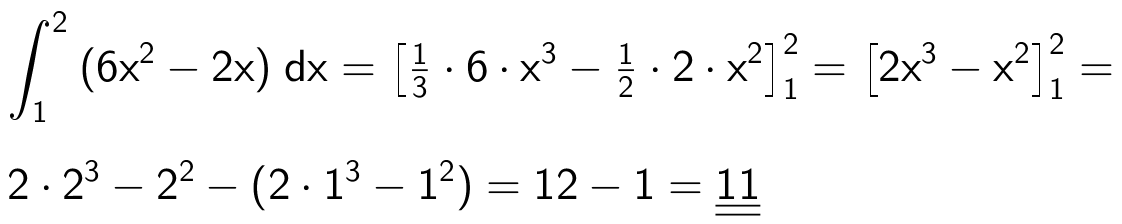
Svar på opgave 4:

1. Alle funktionerne er eksponentialfunktioner. Det, der er forskellen på dem, er deres grundtal.

   A er aftagende, hvilket svarer til en eksponentialfunktion med et grundtal mellem 0 og 1. Dvs. A passer med g(x).

   B og C er voksende hvor B vokser hurtigere end C. Dermed har begge et grundtal større end 1 hvor B's grundtal er større end C's.

   Dette betyder, at B passer med f(x) og C passer med h(x).

Svar på opgave 5:

1. De to sider AC og CE er ensliggende, dvs., at de ligger mellem ens vinkler i hver sin af to ensvinklede trekanter. Det samme gælder for siderne BC og CD. AC og BC tilhører den lille trekant, mens CD og CE tilhører den store.

   Dermed har man, at |CE|/|AC|= |CD|/|BC| ⇒ |CE|/40 = 36/30 ⇒ |CE| = 40·36/30 = 48.

   |BE| = |CE| - |BC| = 48 - 30 = 18

Svar på opgave 6:

1. Cirklen har ligningen (x - 1)² + y² = 8. Man skal løse de sammenhængende ligninger:

   (x - 1)² + y² = 8 og y = x -1 med hensyn til x og y. Man får:

   (x - 1)² + (x -1)² = 8 ∧ y = x - 1 ⇔

   2·(x - 1)² = 8 ∧ y = x - 1 ⇔

   (x - 1)² = 4 ∧ y = x - 1 ⇔

   x - 1 = ±2 ∧ y = x - 1 ⇔

   (x = -1 ∧ y = -2) ∨ (x = 3 ∧ y = 2)

   Skæringspunkterne er (x,y) = (-1,-2) eller (x,y) = (3,2)

Svar på opgave 7:

1. Man opretter vektorerne a og b:

   a:=[5,−10] ▸ [5,−10]

   b:=[6,8] ▸ [6,8]

   Man sætter dem ind i formlen for projektionen af a på b: (dotP(a,b)/norm(b)²)*b ▸ [−3,−4]

   Dvs. projektionen af a på b er (−3,−4)

2. Arealet af det udspændte parallelogram mellem a og b er den numeriske værdi af determinanten til a og b.

   Denne værdi bestemmes som skalrproduktet mellem tværvektoren til a og vektor b.

   Tværvektoren til a, at, oprettes:

   at:=[10,5] ▸ [10,5]

   Man beregner at·b:

   dotP(at,b) ▸ 100

   Dvs. arealet af det udspændte parallelogram er 100

Svar på opgave 8:

1. Man benytter, at trekant BCT er retvinklet, og at der dermed gælder, at: |CT|·cos(∠TCB) = |BC|. Man får, idet ∠TCB kaldes x:

   solve((6371+0.828)*cos(x*1.°)=6371,x)|0<x<90 ▸ x=0.923688

   Dvs. ∠TCB = 0,924°

2. I følge Pythagoras læresætning gælder der for den retvinklede trekant BCT at: |CB|² + |TB|² = |CT|². Heraf får man, idet x = |TB|:

   solve((6371+0.828)²=6371²+x²,x)|x>0 ▸ x=102.718

   Dvs. |TB| = 102,7 km (Det passer ikke helt med tegningen, men det behøver det heller ikke).

Svar på opgave 9:

1. Man opretter lister med antal år efter 1975 og antal bedrifter.

   år:={0,5,15,25,32,33} ▸ {0,5,15,25,32,33}

   bedrifter:={63200,42400,21500,9800,4900,4500} ▸ {63200,42400,21500,9800,4900,4500}

   Man laver eksponentiel regression på de to lister:

   ExpReg år,bedrifter,1: CopyVar stat.RegEqn,f1: stat.results ▸
      [["Titel","Eksponentiel regression"]
      ["RegEqn","a*b^x"]
      ["a",65375.2]
      ["b",0.923589]
      ["r²",0.996446]
      ["r",−0.998222]
      ["Resid","{...}"]
      ["ResidTrans","{...}"]]

   Resulatet af regressionen gennem af Ti-Nspire i en funktion kaldet f1(x). Denne funktion gemmes som N(t):

   n(t):=f1(t) ▸ Udført (Bemærk: x skiftes ud med t i f1(x))

   N(t) udskrives:

   n(t) ▸ 65375.2*(0.923589)^t

   Dvs. N(t) = 65375,2·0,92359^t

2. Halveringstiden for M(t) er ln(1/2)/ln(a) = ln(1/2)/ln(0,98) år = 34,3 år

3. Man opretter funktionen M(t):

   m(t):=1106*(0.98)^t ▸ Udført

   Man opretter funktionen G(t) = M(t)/N(t). Denne angiver antal køer pr. bedrift som funktion af tiden.

   g(t):=m(t)/n(t) ▸ Udført

   G(t) udskrives:

   g(t) ▸ 0.016918*(1.06108)^t

   Det ses at grundtallet, a, for denne funktion er 1,06108. Dette er også fremskrivningsfaktoren for funktionen. Dvs. den årlige vækst er a - 1. Man får:

   Årlig procentvis stigning: (1,06108 - 1)·100 % = 6,11 %

Svar på opgave 10:

1. Man opretter f(x):

   f(x):=35.9*(1-0.493*exp(−0.499*x))^2.604 ▸ Udført

   Nedenfor er tegnet en graf for f.

   

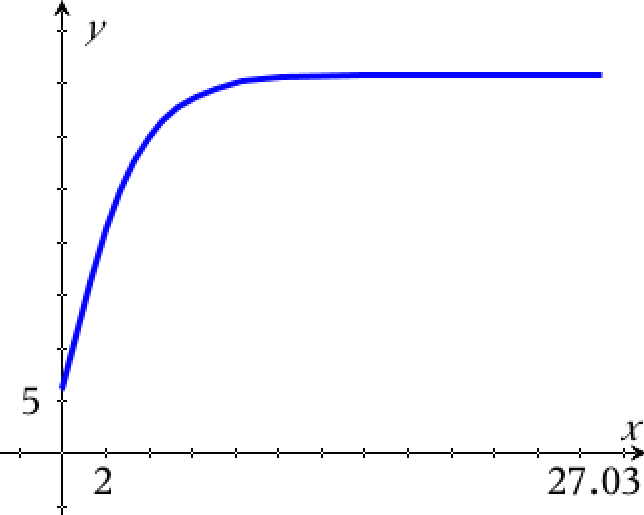
   Man beregner f(10):

   f(10) ▸ 35.5872

   Dvs. udbyttet pr. hektar, når palmerne er 10 år gamle, er: 35,6 tons palmeolie

2. Man beregner f´(5):

   derivative(f(x),x)|x=5 ▸ 1.77498

   Dvs. efter 5 år vokser produktionen af palmeolie pr. hektar med 1,8 tons om året

Svar på opgave 11:

1. Man indsætte koefficienterne for β og koordianterne for punktet G i formlen for afstanden mellem et plan of en linje.

   Koefficienterne til β er a = 23, b = 0 og c = 9, mens koordinaterne til G er x = 16, y = 16 og z = 14

   Tallen indsættes i formlen of afstanden beregnes:

   abs((23*16+0*16+9*14-736.)/sqrt(23²+0²+9²)) ▸ 9.79829

   Dvs. afstanden mellem β og G er 9,798

2. Vektoren CA oprettes:

   ca:=[32,32,0]-[0,32,0] ▸ [32,0,0]

   Denne forkortes med for enkelhedens skyld med 32 og man får vektoren CA2:

   ca2:= [32,0,0]/32 ▸ [1,0,0] (det er unødvendig, men ser pænere ud)

   Vektoren CF oprettes:

   cf:=[23,23,23]-[32,32,0] ▸ [−9,−9,23]

   En normalvektor, n, til planen α er krydsproduktet af CA2 og CF:

   n:=crossP(ca2,cf) ▸ [0,−23,−9]

   En vektor, der ligger i planen α, kan skrives som (x-32,y-32,z), idet den starter i punktet A og ender i punktet (x,y,z) , der antages at ligge i planen.

   Skalarproduktet af denne vektor og normalvektoren, n, for planen vil være 0. Man får:

   dotP([x-32,y-32,z],n)=0 ▸ −23*y-9*z+736=0

   Dvs. ligningen for α er −23y - 9z + 736 = 0

3. Man finder vinklen mellem de to planer ud fra vinklen mellem deres normalvektorer. Normalvektoren til α er n, som man fandt ovenfor.

   En normalvektor til β, m, findes ud fra planens ligning: 23x + 0y + 9z − 736 = 0. Heraf ses at m = (23,0,9).

   Man opretter m:

   m:=[23,0,9] ▸ [23,0,9]

   Vinklen, x, mellem n og m findes ved hjælp af formlen cos(x) = n·m/(|n|·|m|):

   solve(cos(x*1.°)=dotP(n,m)/(norm(n)*norm(m),x)|0<x<180 ▸ x=97.6307

   Dvs. den stumpe vinkel mellem α og β er 97,63°. Hvis der menes vinklen mellem pyramidestubbens flader, så er det også denne vinkel. Dette indses på følgende måde:

   Hvis man hæver toppen af pyramidestubben får man noget, der nærmer sig en kasse. I denne er vinklerne mellem fladerne 90°. Sænker man toppen, så nærmer man sig bunden af pyramidestubben. Her er vinklen mellem fladere 180°. Dvs. vinklen mellem fladerne i en given pyramidesub må være mellem 90° og 180°.

   Vinklen mellem pyramidestubbens flader (den stumpe vinkel mellem α og β) er 97,6°

Svar på opgave 12:

1. Man opretter f(x):

   f(x):=(1/x)*ln(x) ▸ Udført

   Man laver en fortegnsundersøgelse af f´(x):

   solve(derivative(f(x),x)=0.,x)|x>0 ▸ x=2.71828 (nulpunktet for f´(x) bestemmes; x = 2,718)

   derivative(f(x),x)|x=2. ▸ 0.076713 (f´(2)>0)

   derivative(f(x),x)|x=3. ▸ −0.010957 (f´(3)<0)

   Dvs. monotoniforholdende er f vokser for x < 2,718, og aftager for x > 2,718

   Dette viser samtidig, at x = 2,718 er globalt maksimum.

2. Arealet af M er integralet af f(x) fra nulpunktet for f(x) til x = 10.

   Man finder nulpuntet for f(x):

   solve(f(x)=0,x) ▸ x=1

   Dermed er arealet af M lign med integralet af f(x) fra x = 1 til x = 10. Man får:

   integral(f(x),x,1,10.) ▸ 2.65095

   Dvs. arealet af M er 2,651

Svar på opgave 13:

1. Væksthastigheden til det tidspunkt, hvor antal smittede er 100, findes ved at indsætte y = 100 på højre siden af ligningen, da denne er lig med dy/dx som er væksthastigheden for funktionen y(x).

   Man får: 0,00526·100·(209 - 100) = 57,334, dvs. væksten i antallet af smittede er 57,3 om dagen, når der er 100 smittede.

2. deSolve(n'=0.00526*n*(209-n) and n(30)=103,t,n) ▸ n=209.*3.0022^t/(3.0022^t+2.1657·10¹⁴)

   Dvs. N(t) = 209·3,0022^t/(3,0022^t + 2,1657·10¹⁴)

   209 er grænseværdien for antallet smittede, når t går mod uendelig.
   Det følger af omskrivningen: 209·3,0022^t/(3,0022^t + 2,1657·10¹⁴) = 209/(1 + 2,1657·10¹⁴/3,0022^t) som går mod 209 for t gående mod uendelig.

Svar på opgave 14:

1. Rumfanget er arealet af endefladen gange længden af beholderen. Endefladen er en ligesidet trekant med siden x. Denne trekants areal er (√3/4)·x². Længden af beholderen er y.

   Rumfanget er (√3/4)·x²·y = (√3/4)·2²·5 = 8,660

2. Overfladearealet er to gange arealet af en endeflade plus tre gange arealet af en sideflade = 2·(√3/4)·x²· + 3·x·y.

   Man isolerer y i formlen for rumfanget, når rumfaget er 1: (√3/4)·x²·y = 1 ⇒ y = (4/√3)·x^-2. Dette udtryk for y indsættes i formlen for overfladearealet:

   Overflade = 2·(√3/4)·x² + 3·x·(4/√3)·x^-2 = (√3/2)·x² + 4√3·x^-1

3. Man opretter O(x):

   o(x):=sqrt(3)*x²/2+4.*sqrt(3)/x ▸ Udført

   Man finder nulpunkter for O'(x):

   solve(derivative(f(x),x)=0,x) ▸ x=1.5874

   Man undersøger, om dette er det x, der giver det mindste overfladeareal i intervallet 1≤x≤5:

   o(1) ▸ 7.79423

   o(1.5874) ▸ 6.54674

   o(5) ▸ 23.0363

   Dette viser, at x = 1,5874 giver det mindste overfladeareal.