Opgave 1
- Bestem arealet af det indre område.
- Vis at omkredsen af atletikbanen i Skovdalen overholder dette krav.
- Bestem x.
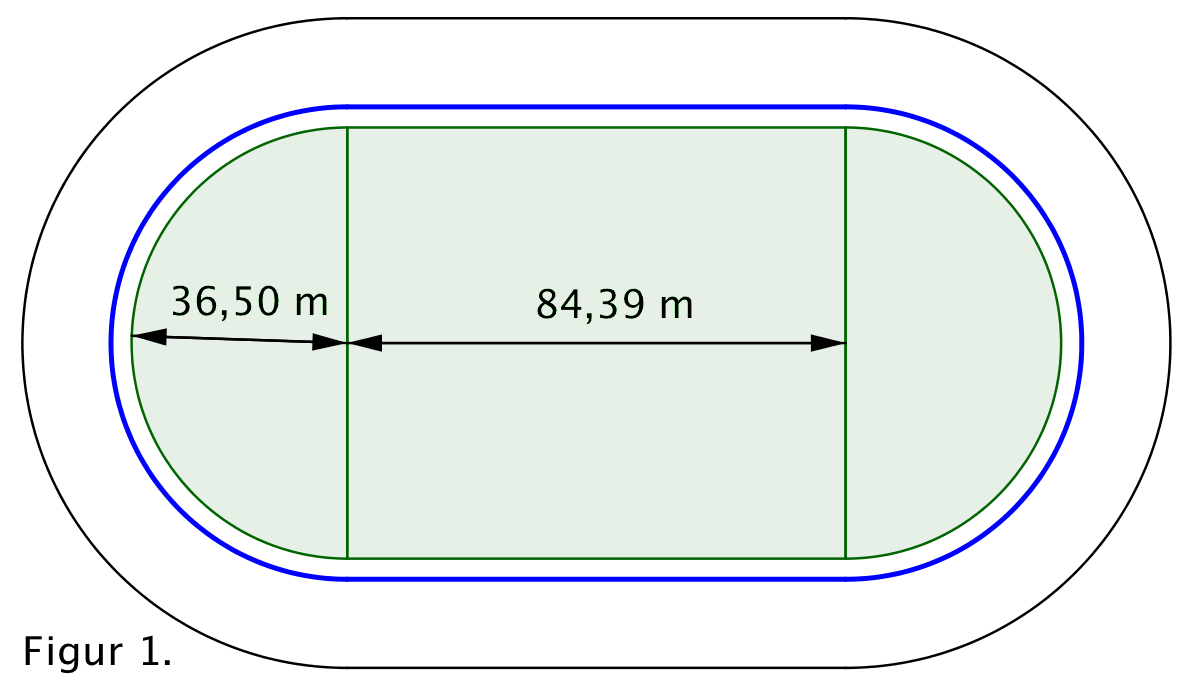
Atletikbanen i Skovdalen i Aalborg afgrænser et område vist med grønt på figur 1. Området har form som et rektangel og to halvcirkler. Længden af rektanglet er 84,39 m og radius af de to halvcirkler er 36,50 m.
Det er et krav, at omkredsen af en officiel atletikbane er 400 m, og den måles 0,30 m fra kanten. På figur 1 er omkredsen af atletikbanen illustreret med blåt.
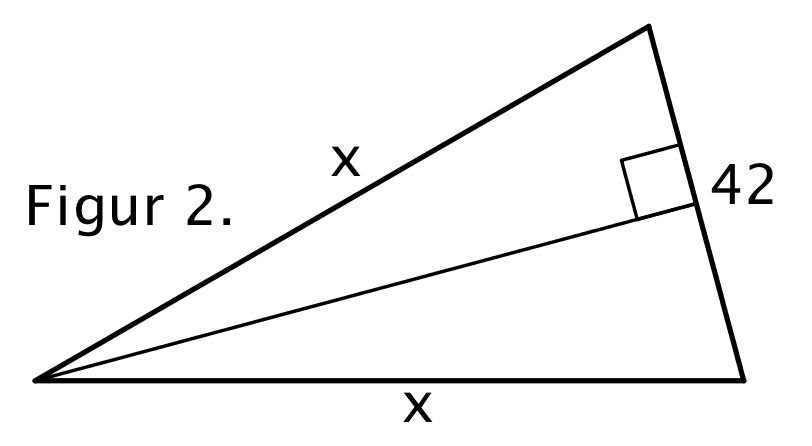
På atletikbanen afholdes også konkurrencer i hammerkast. Det sker på et trekantet område, se figur 2. Trekanten er ligebenet og længden af de to lige lange sider benævnes x. Den tredje side er 42 m. Arealet af trekanten er 1840 m.
Svar på opgave 1:
-
Arealet af det grønne område er summen af arealet af en cirkel med radius 36,50 m og et rektangel med siderne 2·(36,50 m) = 73,00 m og 84,39 m.
Arealet er derfor π·(36,50 m)2 + (73,00 m)·(84,39 m) = 10.346 m2
-
Tegningen nedenfor viser de mål, som man skal bruge for at beregne omkredsen. Den blå linje består af to linjestykker, som er 84,39 m hver og en cirkel med radius 36,50 m + 0,30 m = 36,80 m.

Omkredsen bliver: 2·π·(36,80 m) + 2·(84,39 m) = 400,00 m, hvilket viser at reglen er overholdt.
-
På figuren nedenunder er den ligebenede trekant vist som trekant ABC. Denne indeholder den retvinklede trekant ACD, hvor h er højden i trekant ABC og samtidig katete i trekant ABD.
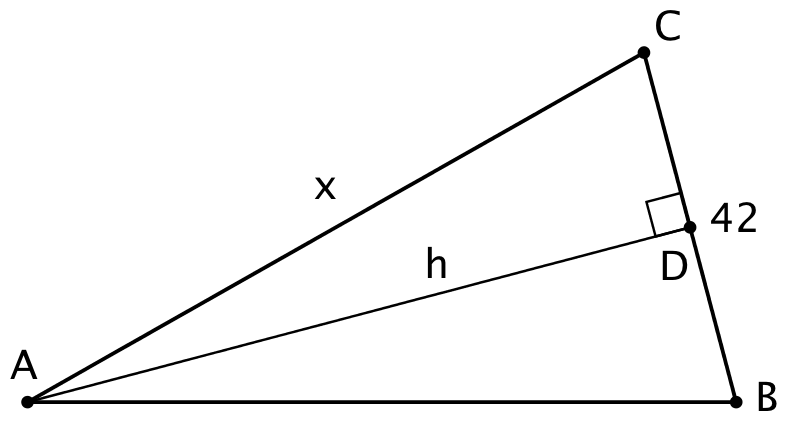
Der gælder at arealet af trekant ABC = 1840 m2 = (1/2)·h·42.
For den retvinklede trekant ABD gælder Pythagoras læresætning: h2 + (21 m)2 = x2.
Man isolerer h i første ligning. Dernæst sættes værdien af h ind i den anden og denne løses med hensyn til x, idet x skal være større end 0:
Ti-Nspire: solve(0.5*42*h=1840 and x2=212+h2,x)|x>0 ▸ x=90.100 and h=87.619 (værdien af h bruges ikke)
Maple: solve([.5*42*h=1840,x2=212+h2,x>0],[x,h]) ▸ [[x=90.100,h=87.619]]
Dvs. siden x i den ligebende trekant er 90,1 m
Opgave 2
- Indtegn data fra tabellen i et passende koordinatsystem.
- Bestem konstanterne a og b.
- Bestem Ledas omløbstid omkring Jupiter.
Omkring planeten Jupiter kredser en række måner i ellipseformede baner. Tabellen nedenfor viser middelafstanden x til Jupiter og omløbstiden T for nogle udvalgte måner.
| Måne | Io | Europa | Ganymedes | Callisto | Themisto |
| Middelafstand, x [mio. km] | 0,422 | 0,671 | 1,07 | 1,88 | 7,39 |
| Omløbstid, T [døgn] | 1,77 | 3,55 | 7,15 | 16,7 | 130 |
Sammenhængen mellem middelafstanden og omløbstiden kan beskrives med potensfunktionen T(x) = b·xa.
Middelafstanden for månen Leda er 11,14 mio. km.
Svar på opgave 2:
-
Nedenstående figur lavet i Ti-Nspire viser til venstre lister over henholdsvis middelafstand og omløbstid. Til højre viser den en kurve af omløbstiden (målt i døgn) som funktion af middelafstanden (målt i mio. km.).
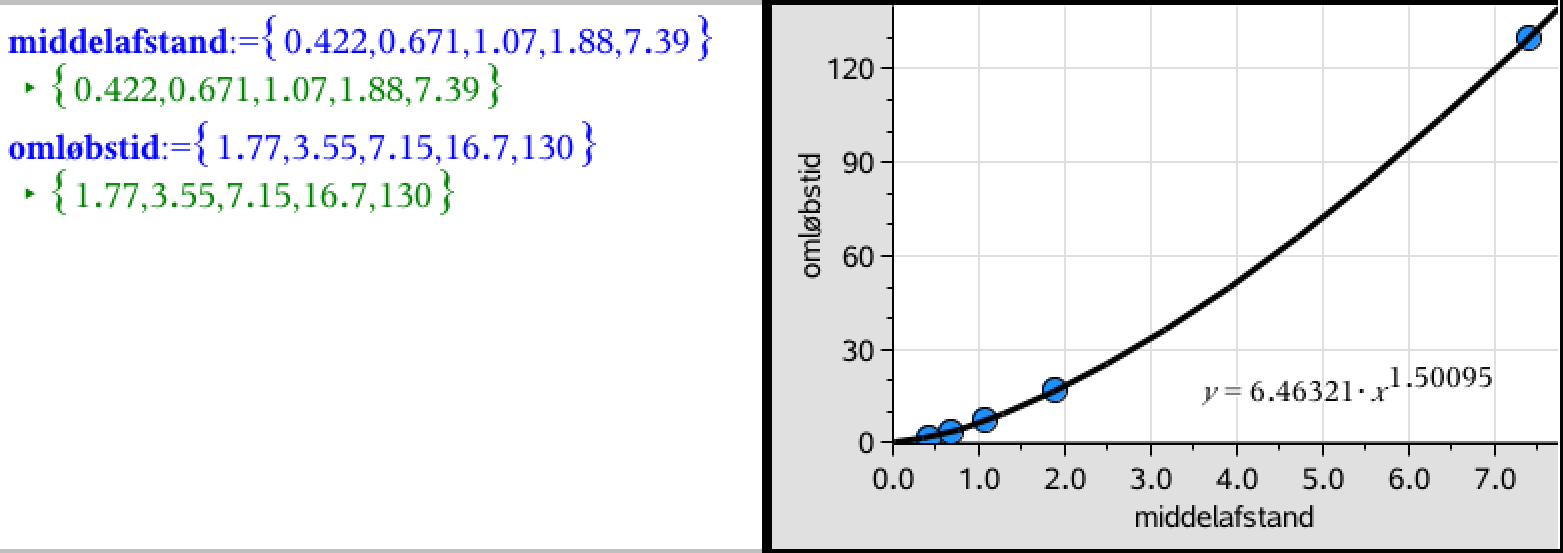
Den kommando, som er brugt, er vist nedenunder. Bemærk at man skal klikke på diagram-feltet (i sort ramme) inden.
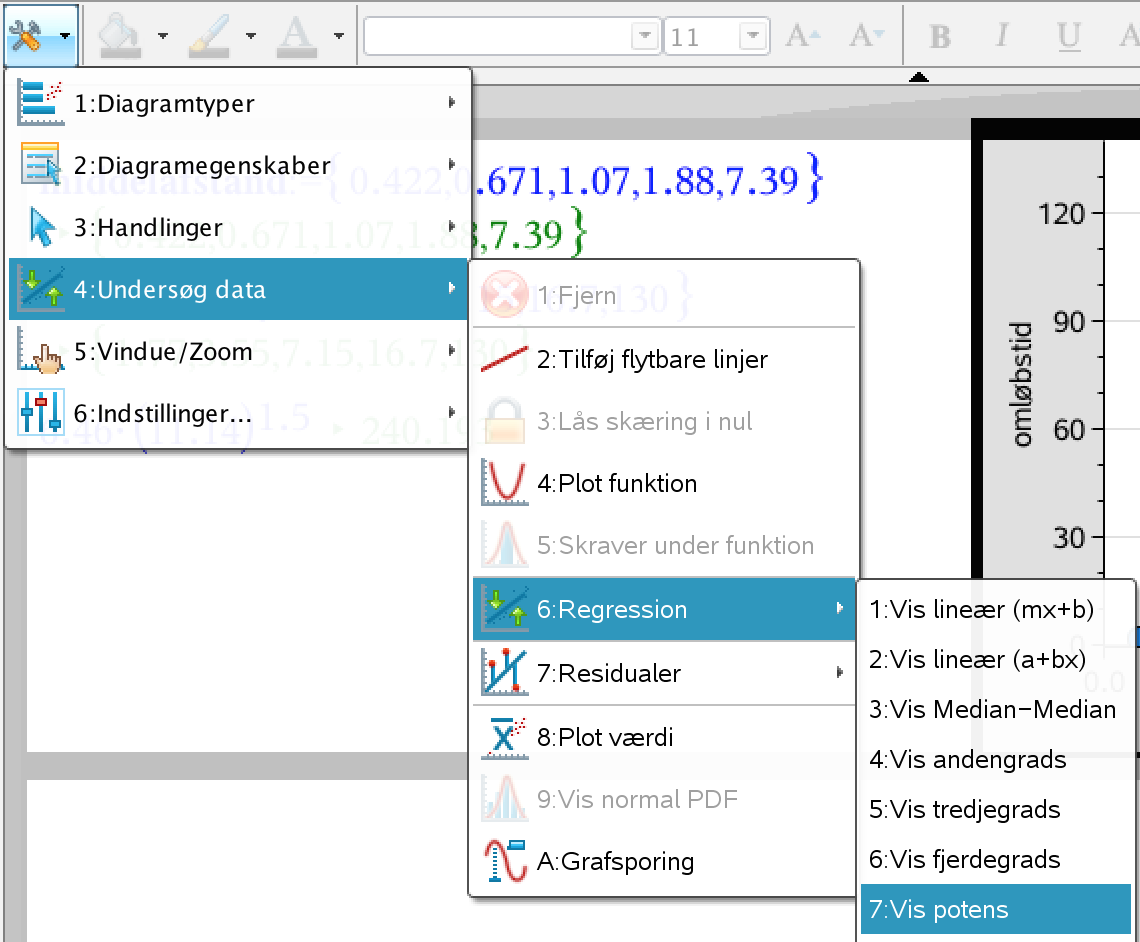
Nedenunder er samme løsning vist i Maple.
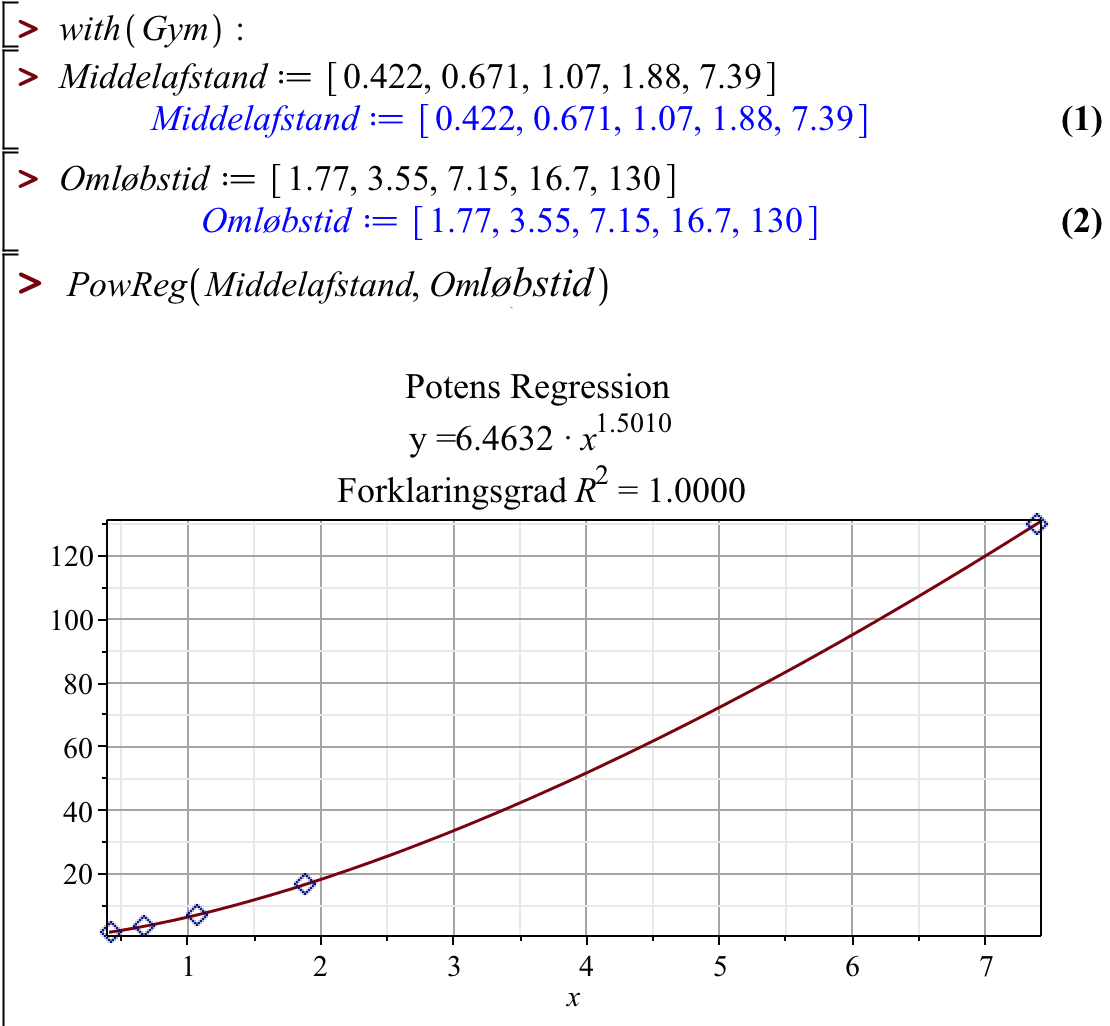
-
På ovenstående figurer er vist regressionsformlen for potensregressionen af de to sæt tal for middelafstand og omløbstid. Formlen fra Ti-Nspire er vist forstørret nedenunder:
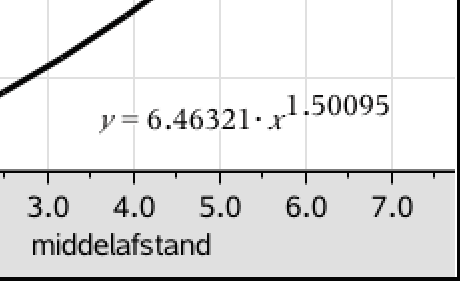
Man får af formlen, at a = 1,50 og b = 6,46
-
Man indsætter værdierne af a og b i formlen for T(x) og får: T(x) = 6,46·x1,50.
Her er x = 11,14, dvs Ledas omløbstid = T(11,14) = 6,46·11,141,50 døgn = 240 døgn
Opgave 3
-
Undersøg om A ligger i α
- Bestem den spidse vinkel mellem α og l
- Bestem en parameterfremstilling for β.
Et punkt A, en plan α og en ret linje i rummet l er givet ved:
A(1;-2;1)
α: 2x + 3y - 4z + 5 = 0
l: (x,y,z) = (1,0,2) + t·(-2,1,2), t ∈R.
Planen β indeholder A og l.
Svar på opgave 3:
-
Hvis A(1;-2;1) ligger i α skal punktets koordinater opfylde α's ligning. Man gør prøve og får:
Venstre side af planens ligning: 2·(1) + 3·(-2) - 4·(1) + 5 = 2 - 6 - 4 + 5 = -3
Højre side af planens ligning: 0
Man ser, at venstre side er forskellig fra højre, så A ligger ikke i α
-
Den spidse vinkel mellem planen α og linjen l kan findes som komplementærvinklen til den spidse vinkel mellem retningsvektoren til l, kaldet r, og α's normalvektor, kaldet n.
Den kan aflæses af koefficienterne til α's ligning. Ligningen er 2x + 3y + (-4)z + 5 = 0, dvs. n = (2,3,-4). Retningsvektoren til l er (-2,1,2).
Man finder vinklen mellem de to vektorer ved indsætte dem i formen for vinklen mellem to vektorer og isolere v (= at løse den fremkomne ligning med hensyn til v):
Ti-Nspire: solve(cos(v*1.°)=dotP([2,3,−4],[−2,1,2])/(norm([2,3,−4])*norm([−2,1,2])),v)|0<v<180 ▸ v=123.855
Den den spidse vinkel mellem retningsvektoren og normalvektoren er 180° - 123,9° = 56,1°
Dermed er vinklen mellem planen og linjen: 90° - 56,1° = 33,9°
... Andre løsninger:
Den samme beregning i Maple:
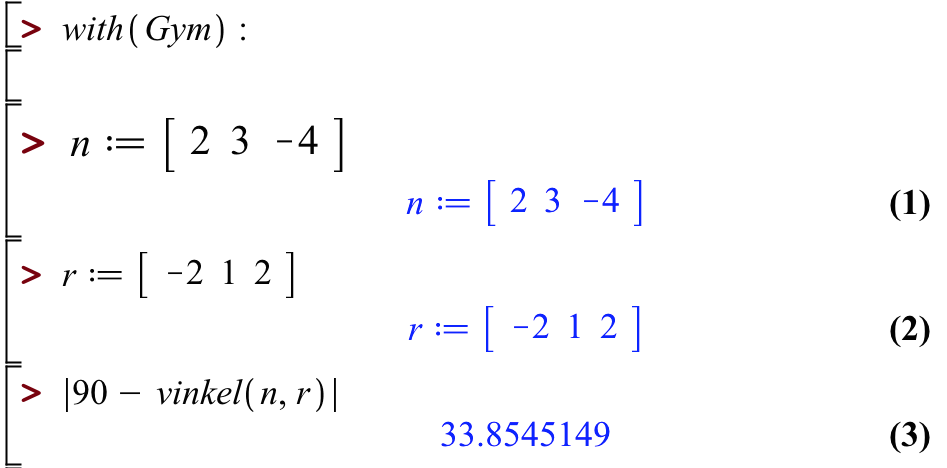
For at indsætte vektorerne er brugt matrix-panelet som vist nedenfor:
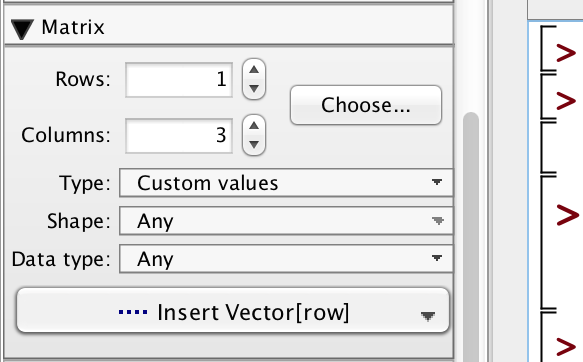
-
Det bemærkes først, at havde punktet A ligget på linjen l, ville der have været uendelig mange muligheder for placeringen af β. Disse planer ville skære hinanden i l.
Man skal bruge to vektorer i planen β, som ikke må være parallelle, for at finde en parameterfremstilling for β.
Man har retningsvektoren r fra linjen og kan finde den anden vektor ved at forbinde punktet (1,0,2) på linjen med punktet A. Denne vektor kaldes m. Man får, at m = (1,-2,1) - (1,0,2) = (0,-2,-1), som ganges med -1, så den giver (0,2,1) for at få pænere tal. Desuden ved man, at (1,0,2) ligger i planen (man kan også vælge A). Dette giver følgende parameterfremstilling for β:
β: (1,0,2) + s(-2,1,2) + u(0,2,1), s og u ∈ R
Opgave 4
-
Vis at P(M) = 0,22.
-
Bestem P(G|M).
-
Afgør om de to hændelser M og G er uafhængige.
På et gymnasium vil man undersøge sammenhængen mellem at være matematiklærer og at være gråhåret. En optælling viser, at 40 % af lærerne er gråhårede og 25 % af de gråhårede er matematiklærere. Blandt de ikke-gråhårede er 20 % matematiklærere.
Man vælger en tilfældig lærer. Følgende hændelser defineres:
M: Den valgte lærer er matematiklærer
G: Den valgte lærer er gråhåret.
Svar på opgave 4:
-
Nedenstående tegning viser forholdet mellem de forskellige typer af lærere. Det antages, at antallet af lærere på skolen er 100.

P(M) er sandsynligheden for at vælge en matematiklærer tilfældigt blandt alle lærere. Dvs. man skal finde andelen af matematiklærere på skolen.
Man betragter en skole med 100 lærere. 40 af disse er gråhårede og af de gråhårede er 25 % matematiklærere, dvs. der er 40·0,25 = 10 gråhårede matematiklærere på skolen.
Tilsvarende får man for de lærere, der ikke er gråhårede, at der er 60·0,20 = 12 matematiklærere, der ikke er gråhårede på skolen.
I alt er der 10 + 12 = 22 matematiklærere ud af 100 lærere på skolen eller 22 % af alle lærere.
Dermed er P(M) = 0,22.
-
P(G|M) er sandsynligheden for at have trukket en gråhåret, når man ved at den, som man har trukket er matematiklærer, hvilket er det samme som sandsynligheden for at trække en gråhåret blandt matematiklærerne. Igen betragtes tegningen fra før.
Der er 22 matematiklærere. 10 af dem er gråhårede. Andelen af gråhårede matematilærere ud af alle matematiklærere er dermed 10/22 = 0,455.
Dvs. P(G|M) = 0,455
-
De to hændelser G og M er ikke uafhængige, idet P(G) ≠ P(G|M).
Man har nemlig, at P(G) = andelen af gråhårede ud af alle lærere = 40 % og P(G|M) = 0,455 = 45,5 %.
Bemærkning:
Hvis andelen af matematiklærere havde været ens (f.eks. 25 %) for både gråhårede og ikke-gråhårede lærere, så havde de to hændelser M og G været uafhængige. I så fald havde man nemlig fået:
P(G) = 40 % og P(G|M) = 10/(10 + 0,25·60) = 10/(10 + 15) = 10/25 = 40 %. Dvs. det ville ikke ændre sandsynligheden for at have trukket en gråhåret, at man havde fået at vide, at den man havde trukket var matematiklærer. Denne situation er vist nedenunder:

Bemærk i øvrigt, at uafhængige hændelser ikke er det samme som disjunkte hændelser. Uafhængig betyder, at den ene hændelse ikke ændrer sandsynligheden for den anden. Disjunkte betyder, at den ene udelukker den anden, dvs. at en lærer ikke både kan være gråhåret og matematiklærer.
Opgave 5
-
Bestem monotoniforhold for f.
-
Vis at ligningen for t er givet ved:
y = -0,44x + 2,152
-
Bestem arealet af det tonede område.
- Færdiggør forklaringen i trin 2 og redegør for trinene (3) og (4) samt argumenter for, at tangenterne i -x0 og x0 altid er parallelle.
En funktion er givet ved
f(x) = (-1/3)·x3 + x + 1
For x = 1,2 har grafen for f en tangent, t.
Det tonede område på figur 3 er afgrænset af t (sort linje) og grafen for f (grøn kurve).
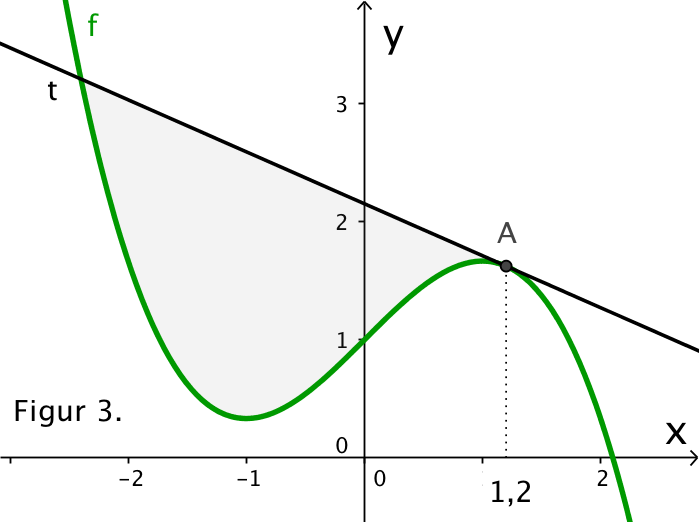
Ved hjælp af nedenstående beregninger kan man vise, at tangenterne til grafen for f i -x0 og x0 altid vil være parallelle.
(1) f(x) = (-1/3)·x3 + x + 1... Forskriften for f opskrives.
(2) f'(x) = 3·(-1/3)·x2 + 1... f differentieres ved hjælp af...
(3) f´(-x0) = -(x0)2 + 1...
(4) f´(x0) = -(x0)2 + 1 ...
Svar på opgave 5:
-
Man laver en fortegnsundersøgelse af f'. Dette gøres ved at finde nulpunkter for f' og dernæst bestemme fortegn for f' omkring nulpunkterne. Dette er gjort i Ti-Nspire nedenfor:
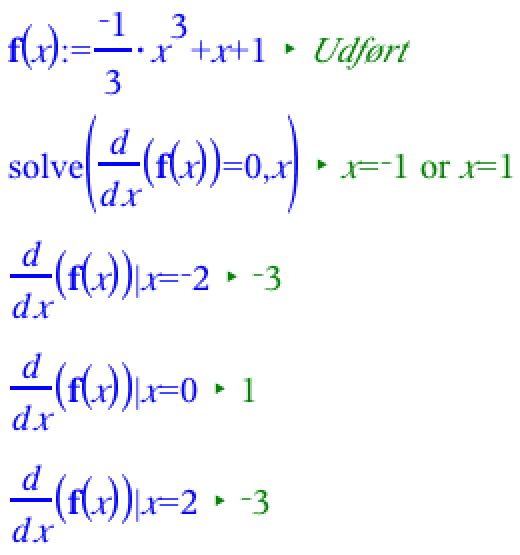
Dvs. f er aftagende for x mindre end -1, voksende for x liggende mellem -1 og 1 og aftagende for x større end 1
Fremgangmåden er den samme i Maple, idet man bruger f´(x) i stedet for d(f(x))/dx. Desuden bruger man f´(-2) i stedet for d(f(x))/dx|x=-2.
-
Tangentens ligning er givet ved formlen y = f´(1,2)·(x - 1,2) + f(1,2). Man har at f´(x) = -x2 + 1, dvs
y = (-(1,2)2 + 1)·(x - 1,2) + (-1/3)·(1,2)3 + x + 1 ⇔
y = -0,44x + 2,152, hvilket skulle vises.
-
For at finde arealet mellem kurverne, skal man først finde x-værdierne af deres skæringspunkter. Dette gøres ved at løse ligningen f(x) = y = -0,44x + 2,152, med hensyn til x. Man får i Ti-Nspire:
solve(f(x)=−0.44*x+2.152,x) ▸ x=−2.4 or x=1.2
(Det samme som Maple bortset fra, at man ikke her skriver ",x" til sidst i solve-udtrykket).
Dvs. skæringspunkternes x-værdier er x = -2,4 og x = 1,2. Man finder nu arealet mellem f og t som den numeriske værdi af integralet af f(x) - (-0,44x + 2,152) fra x = -2,4 til x = 1,2. Dette giver i Ti-Nspire:
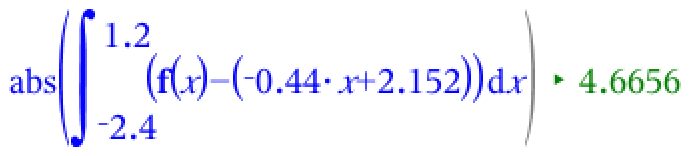
Dvs. arealet af det tonede område er 4,67
-
(2) f'(x) = 3·(-1/3)·x2 + 1...f differentieres ved hjælp af reglerne for stykvis differentiering og differentiering af potensfunktioner
(3) f´(-x0) = -(x0)2 + 1...Man finder den afledede af f for x lig med -x0
(4) f´(x0) = -(x0)2 + 1 ...Man finder den afledede af f for x lig med x0
Da f´(x0) = f´(-x0) vil hældningen til tangenten til grafen for f være ens for x = -x0 og x = x0 og dermed er de to tangenter parallelle. Et eksempel er vist nedenunder for x = -1,2 og x = 1,2:

Opgave 6
-
Beregn tslut
-
Bestem koordinatsættet til P
-
Beregn den maksimale højde af slaget.
-
Bestem farten af tennisbolden i det øjeblik, den passerer over nettet.
På figur 4 er en tennisbolds banekurve indlagt i et koordinatsystem fra slagets begyndelse (til venstre) til bolden rammer jorden på den anden side af nettet.

Tennisboldens kurve er bestemt med følgende vektorfunktion:
r(t) = (x(t),y(t)) = (14,8t;-4,9t2+3,3t+1,1), t=[0;tslut]
hvor tiden t måles i sekunder, afstanden måles i meter og tslut er det tidspunkt, hvor bolden rammer jorden.
Nedslagspunktet P er vist på figur 4.
Nettet er placeret ved x = 7.
Svar på opgave 6:
-
Bolden rammer jorden, når y(t) = 0. For at finde tslut skal man derfor løse ligningen: -4,9·t2 + 3,3·t + 1,1 = 0 (for t > 0). Dette er gjort nedenunder:
Ti-Nspire: solve(−4.9*t2+3.3*t+1.1=0,t)|t>0 ▸ t=0.918
Maple: solve([-4.9*t2+3.3*t+1.1 = 0, t > 0], t) ▸ {t = 0.9180091987}
Dvs. tslut = 0,92 s
-
Man skal finde x-værdien af nedslagspunktet. Denne værdi er lig med x(tslut) = 14,8·0,92 m = 13,59 m.
Dvs. P = (13,6;0) med enheden meter.
-
Man skal finde tmaks, der er den værdi af t, som giver maksimumværdien af y(t). Dette gøres ved at finde det t, hvor y'(t) = 0.
Man får: y'(t) = -9,8·t + 3,3. Dette giver: y'(tmaks) = 0 ⇒ -9,8·tmaks + 3,3 = 0 ⇒ tmaks = 0,3367
Maksimum-værdien er y(tmaks) = -4,9·(tmaks)2 + 3,3·tmaks + 1 = -4,9·(0,3367)2 + 3,3·0,3367 + 1,1 = 1,6556.
Dvs. det højeste punkt på kurven er 1,66 m
-
Farten af bolden, når bolden passerer nettet, er lig med |r'(tnet)|, hvor tnet er det tidspunkt, hvor bolden passerer nettet, dvs. det t, hvor x(t) = 7.
r'(t) = (14,8;-9,8t+3,3)
Man finder tnet i Ti-Nspire:
solve(14.8*t=7,t) ▸ t=0.47297
Dvs. tnet = 0,473. Man finder |r'(0,473)| = √[14,82+(-9,8·0,473+3,3)2] = 14,860.
Dvs. farten, idet bolden passerer nettet, er 14,86 m/s