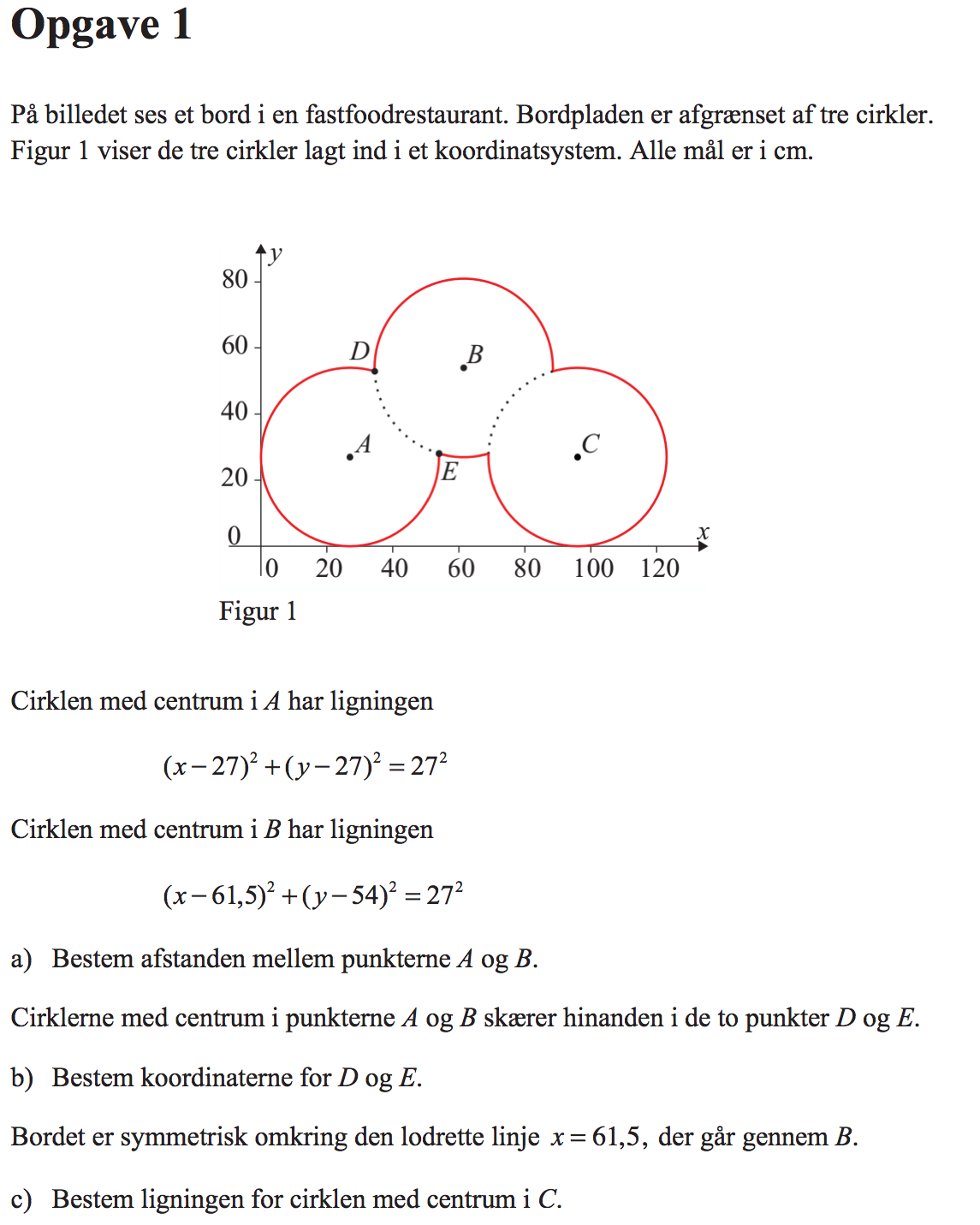
Svar på opgave 1:
Løsning i Ti-Nspire:
-
Ved hjælp af afstandsformlen får man:

Afstanden mellem A og B er 43,8
-
Man løser et lignings-system med ligningerne for de to cirkler:
solve((x-27)2+(y-27)2=272 and (x-61.5)2+(y-54)2=272,x,y) ▸
x=34.521159 and y=52.9313 or x=53.9788 and y=28.0687
Man får, at D = (34,5;52,9) og E = (54,0;28,1)
-
Punktet C har samme y-koordinat som A (27,0). B's x-koordinat (xB) ligger midt mellem x-koordinaten for A (xA) og x-koordinaten for C (xC). Der gælder derfor, at xC = xB + (xB - xA) = 61,5 + (61,5 - 27,0) = 96.
Dvs. C = (27,96). Cirklen har radius = 27, og dens ligning bliver dermed: (x - 96)2 + (y - 27)2 = 272
Løsning i Geogebra:
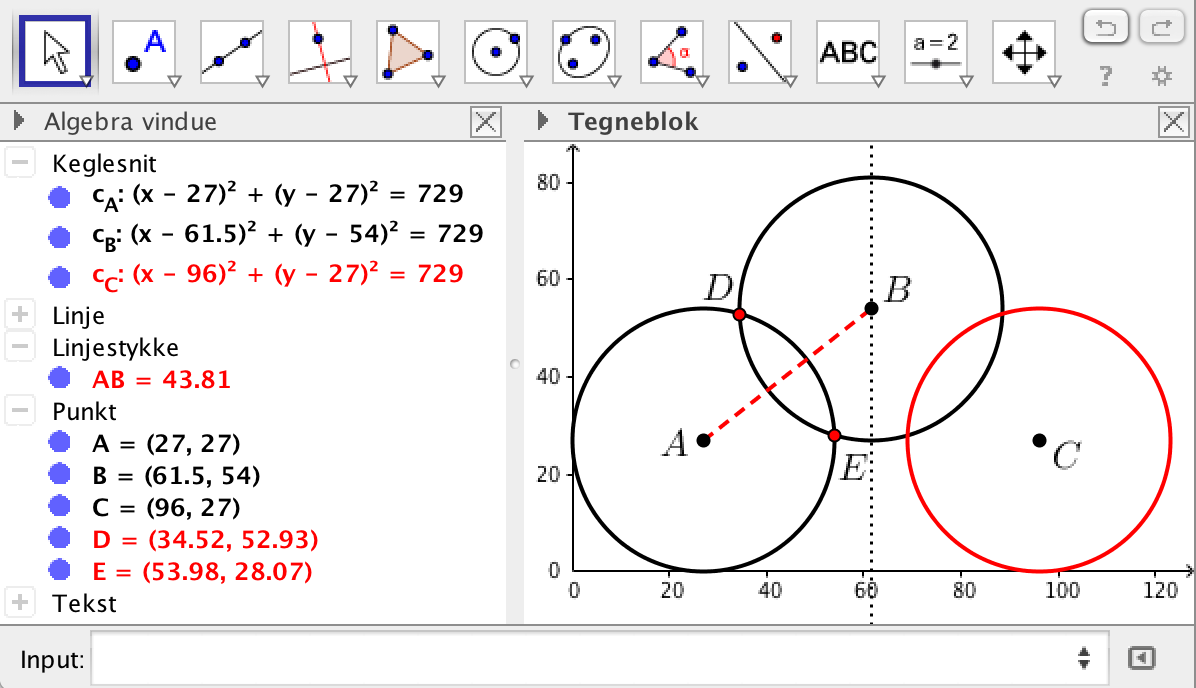
Først skrives ligningen for cirklerne med centrum i A og B ind i input-feltet. Dermed er de to cirkler oprettet.
-
Afstanden mellem A og B findes ved at trykke på afstands-værktøjet (under vinkel-værktøjet) og dernæst på punkt A og B. Afstanden måles til: 43,81, som vist midtpå til venstre på billedet.
-
Man klikker på skærings-værktøjet (under punkt-værktøjet) og klikker på cirklen med centrum i A og cirklen med centrum i B. Skæringspunkterne D og E bliver oprettet. Deres koordinater aflæses til venstre som: D = (34,5;52,9) og E = (54,0;28,1)
-
C oprettes ved spejling af A i den stiplede linje gennem B. Koordinaterne aflæses i algebra vinduet.

Svar på opgave 2:
Løsning i Ti-Nspire:
-
Vinklen v (i radianer) findes af formlen r·sin(0,5·v) = 0,5·k:
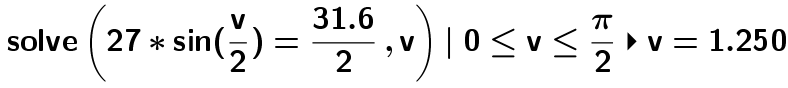
Omregnet til grader giver det: v = 1,25*180°/π = 71,6°
-
Arealet er summen af arealerne af de tre cirkler minus arealerne af de to overlap. Hvert overlap består af to cirkelafsnit som vist på figuren nedenunder:
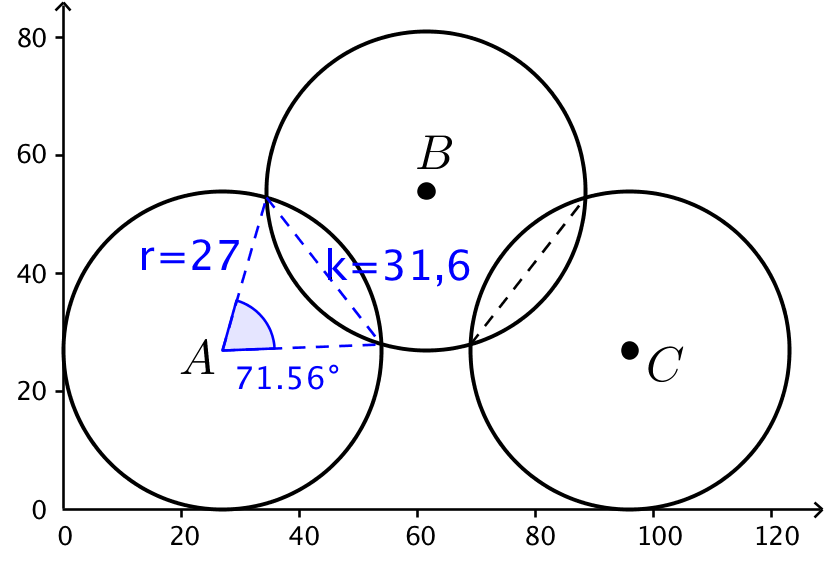
Hver cirkel har arealet π·r2 = π·272, mens hvert cirkelafsnit har arealet: 0,5·r2·(vrad - sin(vrad)) = 0,5·272·(1,25 - sin(1,25)). Dette giver bordets areal: 3·π·272 - 4·0,5·272·(1,25 - sin(1,25)) = 6.431,8
-
Omkredsen er summen af omkredsen af de tre cirkler minus længden af buerne for de to overlap. Omkredsen for den enkelte cirkel er 2·π·r. Den enekelte bue i overlappene har længden: r·vrad. Omkredsen bliver: 3·2·π·r - 4·r·vrad = 3·2·π·27 - 4·27·1,25 = 374,0
Løsning i Geogebra:
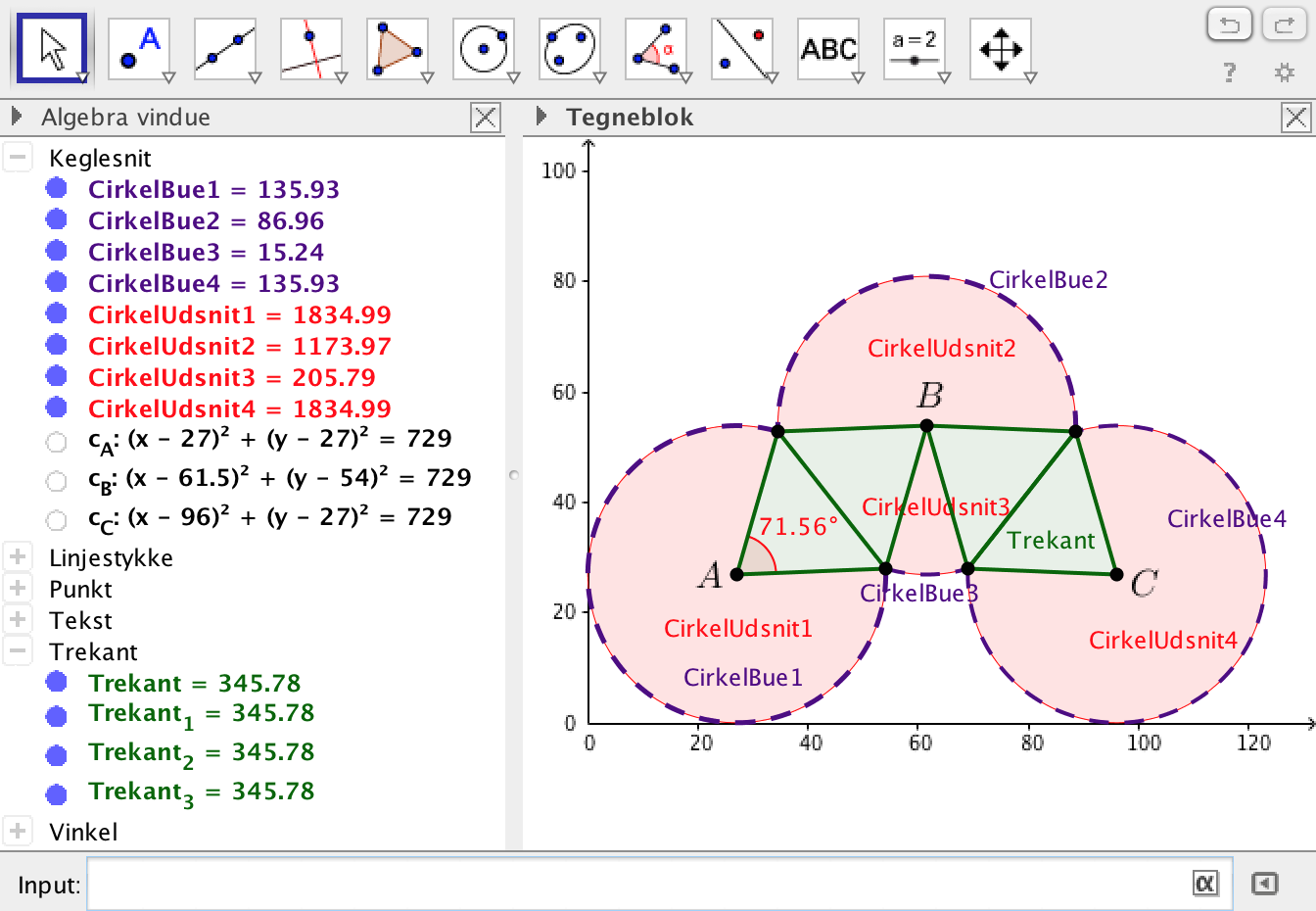
-
Vinklen v måles med vinkel-værktøjet til 71,6°
-
Arealet er summen af arealerne af de fire cirkeludsnit og de fire trekanter: 2·1.834,99 + 1.173,97 + 205,79 + 4·345,78 = 6.432,9
-
Omkredsen er summen af længderne af de fire cirkelbuer: 2·135,93 + 86,96 + 15,24 = 374,1

Svar på opgave 3:
-
Kurven for r(t) tegnet i Geogebra. A er startpunkt (t = 0) og B er slutpunkt (t = 4,5).
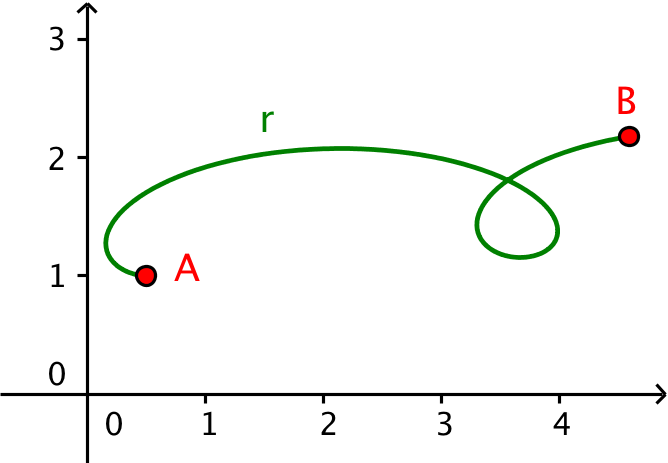
-
A = r(0) = [(2·0 - 2·sin(2·0) + 1) / 2, (0 - 10·cos(2·0) + 30) / 20] = (0,5;1)
B = r(4,5) = [(2·4,5 - 2·sin(2·4,5) + 1) / 2, (4,5 - 10·cos(2·4,5) + 30) / 20] = (4,588;2,181)
-
Man skal finde |r'(2,25s)|.
r'(t) = (-2 cos(2·t) + 1, sin(2t) + 1/20). Det giver at |r'(2,25s)| = |(-2 cos(2·2,25) + 1, sin(2·2,25) + 1/20)| = |(1,422;-0,928)| = √[1,4222 + (-0,928)2] = 1,697
-
Man skal finde størsteværdien af y(t) = (t - 10·cos(2·t) + 30) / 20, for 0 ≤ t ≤ 4,5 sek.
Man undersøger ekstremer og sammenligner dem med endepunkter.
Eksrema findes som nulpunkter for y'(t). Man har at y'(t) = sin(2t) + 0.05. Man får: y'(t) = 0 ⇒ sin(2t) + 0.05 = 0.
Dette løses i TiNspire: solve(sin(2*t)+0.05=0.,t)|0≤t≤4.5 ▸ t=1.59581 or t=3.11658
Ekstremumsværdierne er y(1.59581) = 2.0791 og y(3.117) = 1.156. Endepunkterne er y(0) = 1 og y(4,5) = 2,181.
Den størte værdi af disse fire er y(4,5) = 2,181, som er maksimum-højden for sommerfuglen.

Svar på opgave 4:
Løsning i Ti-Nspire.
-
Kuglens centrum er C = (3,5,4). Dens radius er |AC| = |(3 - 1, 5 - 2,4 + 2)| = |(2,3,6)| = √[22 + 32 + 62] = √[49] = 7. Kuglens ligning er: (x - 3)2 + (y - 5)2 + (z - 4)2 = 72
-
|BC| for k = 3 er lig med: |(3 + 1,5 - 3,4 - 3)| = |(4,2,1)| = √[42 + 22 + 12] = √[21] = 4,583
-
Man skal løse uligheden |BC| < 7 dvs. afstanden mellem b og C skal være mindre end radius.
Man får: |BC| < 7 ⇒ |(4,5-k,1)| < 7 ⇒ √[42 + (5-k)2 + 12] < 7 ⇒ √[k2 - 10·k + 42] < 7 ⇒ k2 - 10·k + 42 < 49. Dette løses i Ti-Nspire:
solve(k2 - 10.*k - 7 < 0,k) ▸ −0.657 < k < 10.66.
Dvs. de k-værdier, der giver punkter af B inden for kuglen er: -0,657 ≤ k ≤ 10
Løsning i Geogebra.
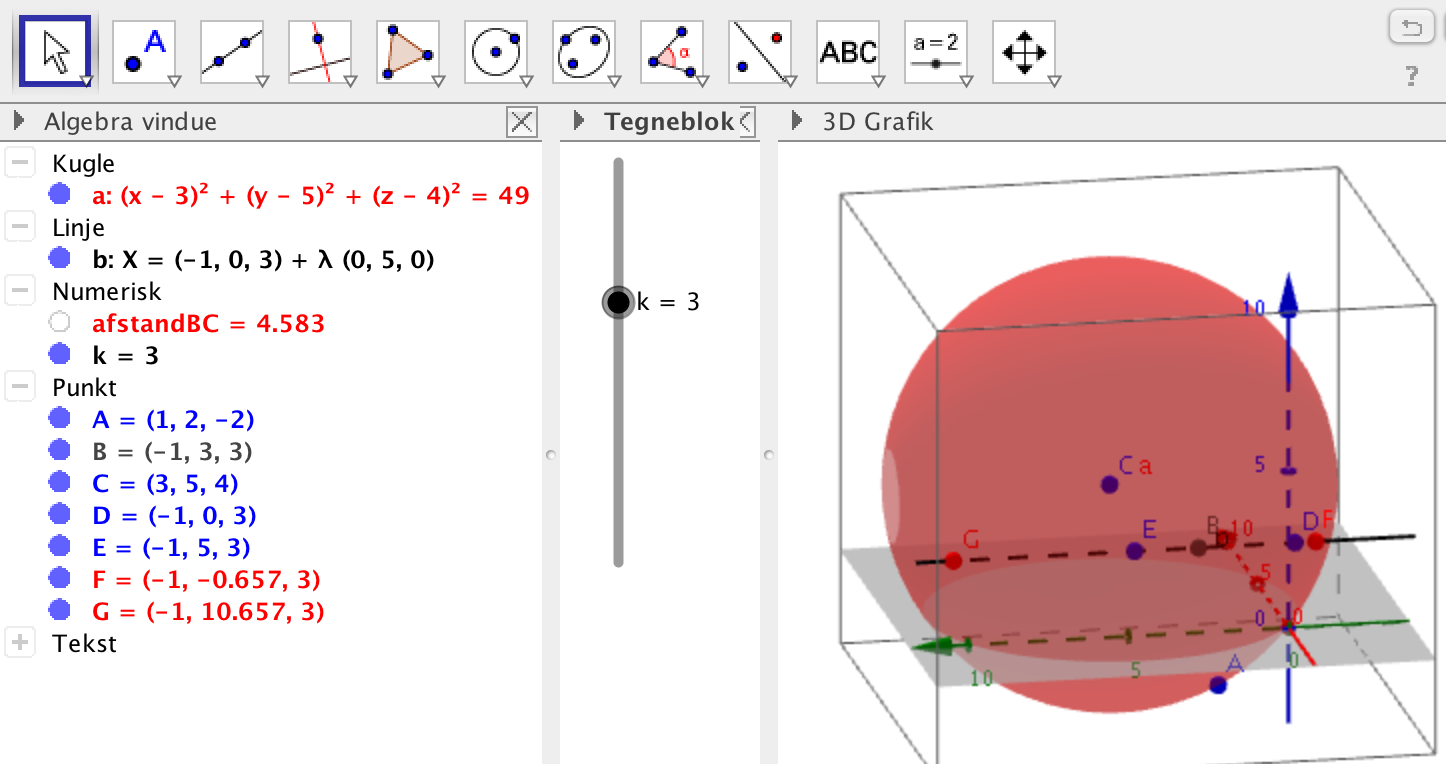
De tre punkter A, B og C indsættes i 3D grafik modulet. Der oprettes en skyder for k defineret mellem -10 og 10.
-
Ved hjælp af kugle-værktøjet oprettes en kugle med centrum i C og med radius AC. Denne kugles ligning aflæses til venstre for oven til: (x - 3)2 + (y - 5)2 + (z - 4)2 = 72
-
k sættes lig med 3 og afstanden mellem B og C måles med afstands-værktøjet (under vinkel-værktøjet) til 4,583
-
Man opretter en linje gennem B for k = 1 og B for k = 2. Alle B'er ligger på denne linje. Ved hjælp af skærings-værktøjet findes skæringen mellem kuglen og denne linje. y-koordinaterne for skæringspunkterne er -0,657 og 10,657.
Dvs. de k-værdier, der giver punkter af B inden for kuglen er: -0,657 ≤ k ≤ 10


Svar på opgave 5:
-
Grafen nedenunder er tegnet i Geogebra ved at skrive x^3 - 12 i input-feltet og trykke enter.
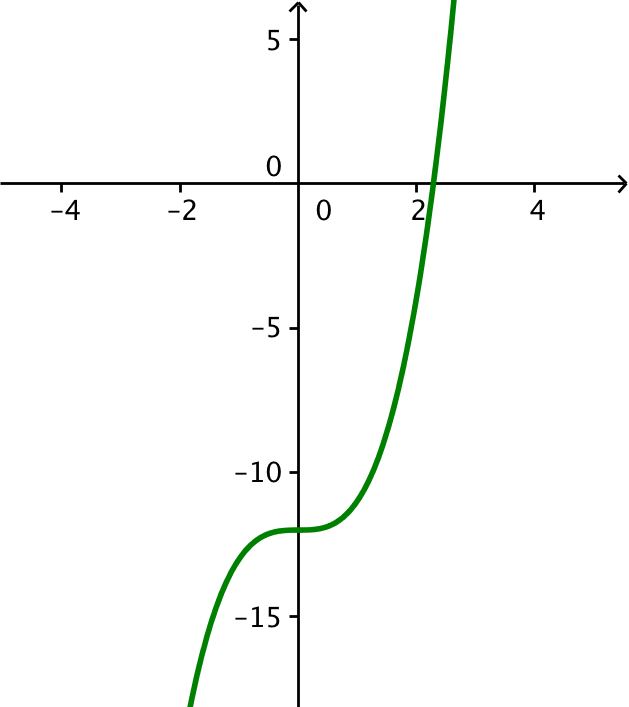
-
Funktionen f er voksende for alle x, idet f´(x) = 3·x2, som er større end eller lig med 0 for alle x.
-
Ti-Nspire: Man opretter funktionen g(x) = xn+1. I den indsættes startværdien x0 = 1. Herefter findes g(1) og derpå g(ans). Dette gentages ved at trykke enter, indtil man får samme værdi to gange i træk. (Man skal være i "Beregninger" - ans virker ikke i "Noter")

Princippet i en grafisk løsning med fire iterationer er tegnet nedenunder i Geogebra. Man tager tangenten til kurven i xi. Der hvor denne tangent skærer x-aksen er xi+1. Dette gentages indtil forskellen på to på hinanden følgende værdier af xi bliver tilstrækkelig lille.
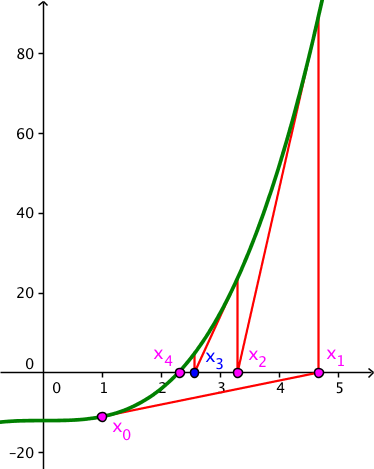
-
(2) Funktionen f og dens afledede indsættes i rekursionsligningen
(3) Led med xn og 1/xn2 samles hver for sig
(5) Rekursionsligningen faktoriseres.
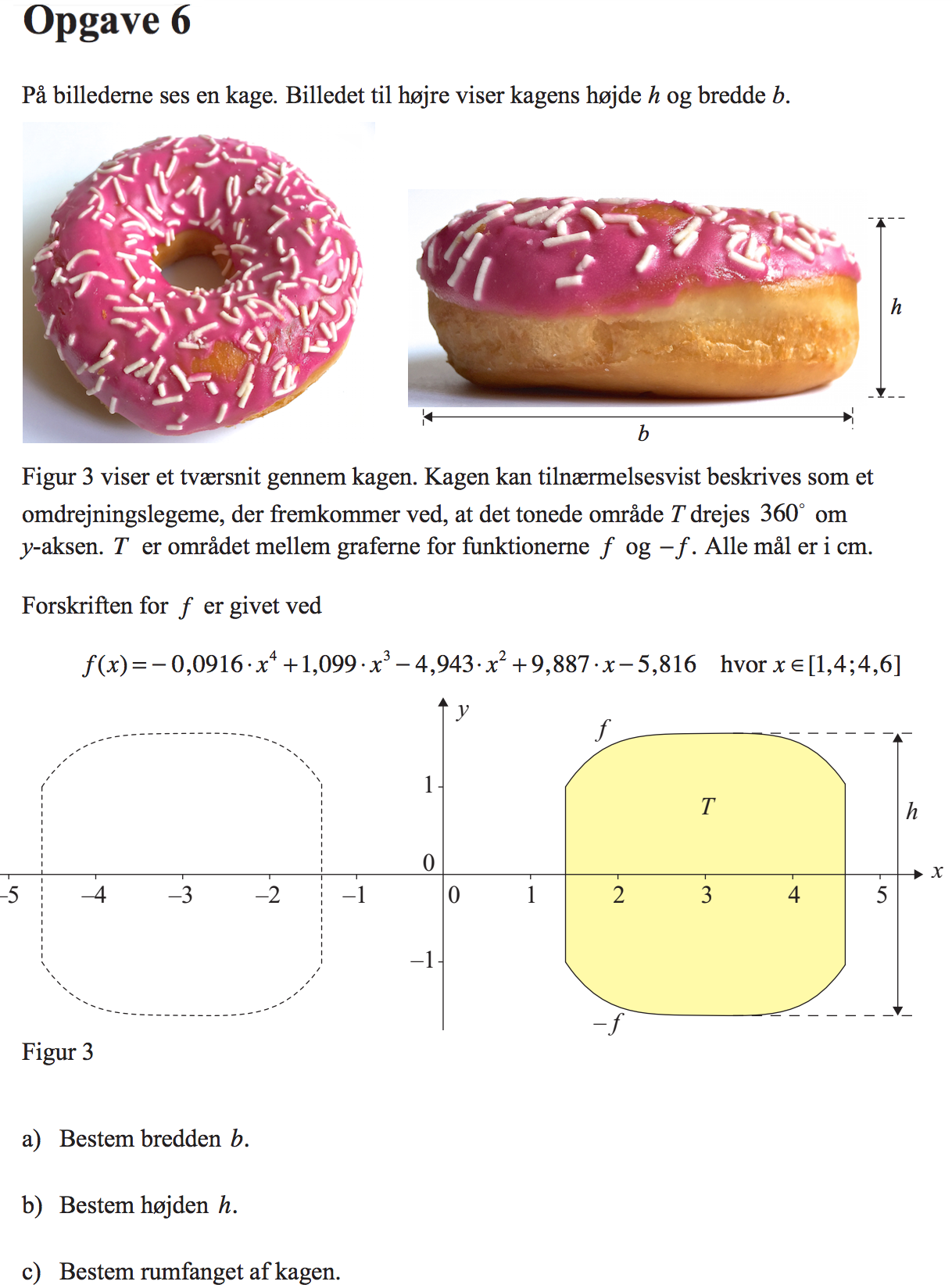
Svar på opgave 6:
-
Bredden b er 2·4,6 cm = 9,2 cm
-
Højden h er 2 gange maksimum-værdien af f. Maksimum-værdien af f findes at bestemme nulpunkter for f´(x). Dette gøres i Ti-Nspire:
f(x):=−0.0916*x4+1.099*x3-4.943*x2+9.887*x-5.816|1.4≤x≤4.6 ▸ Udført
df(x):=d(f(x))/dx ▸ Udført
solve(df(x)=0,x) ▸ x=3.3022
f(3.3022) ▸ 1.6136
Dvs. h = 2·1,6136 cm = 3,23 cm
-
Rumgfanget af omdrejningslegemet beregnes i Ti-Nspire (der er tale om rotation om y-aksen):
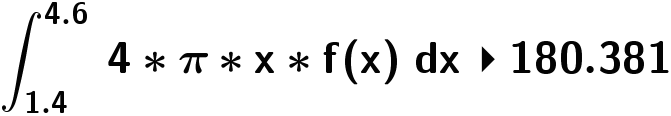
Rumfanget er 180,4 cm3