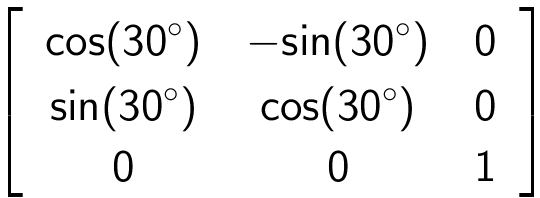
Svar på opgave 1 (Slangemur):

Løst i Geogebra:

Det fremgår af billedet at:...

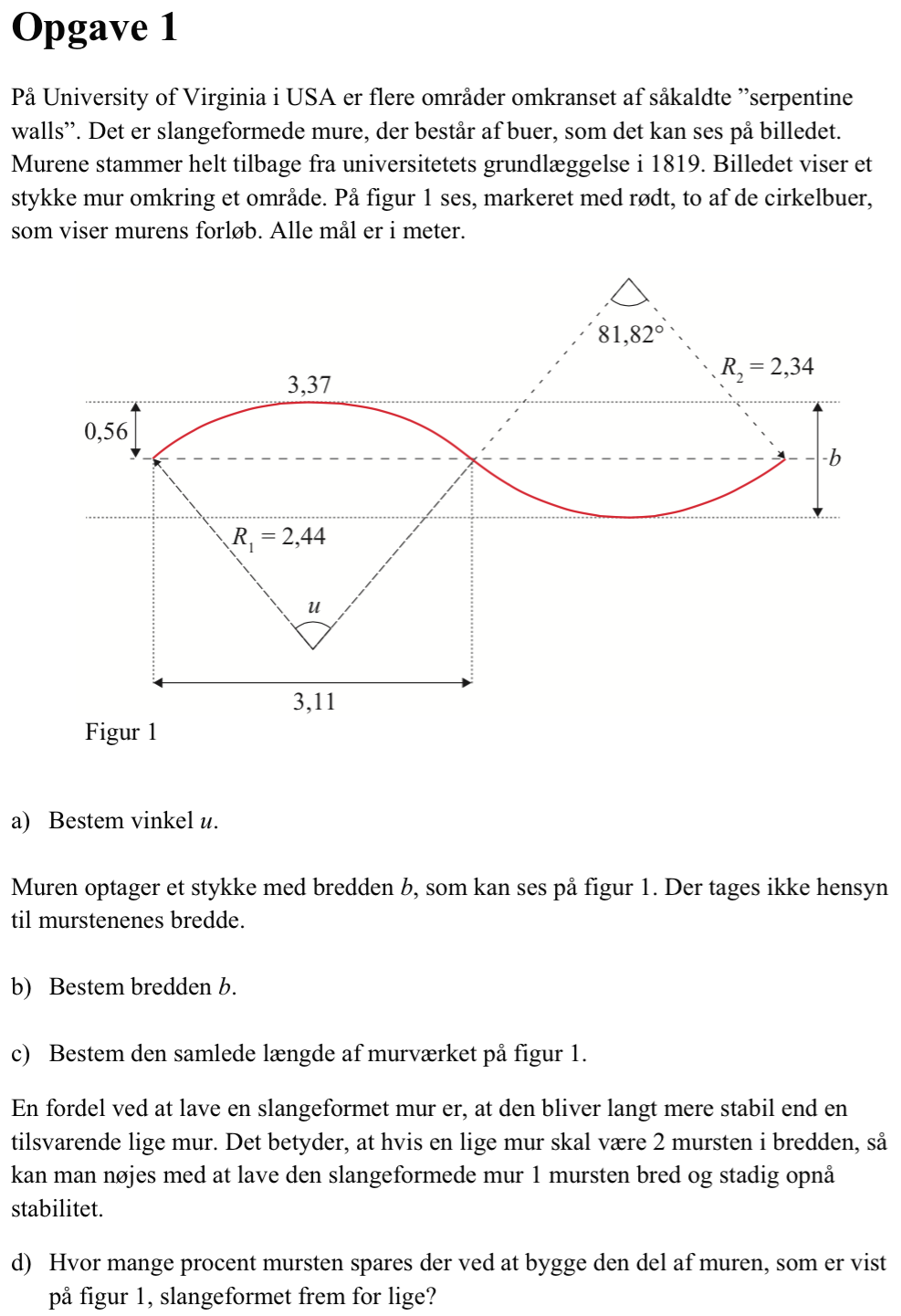
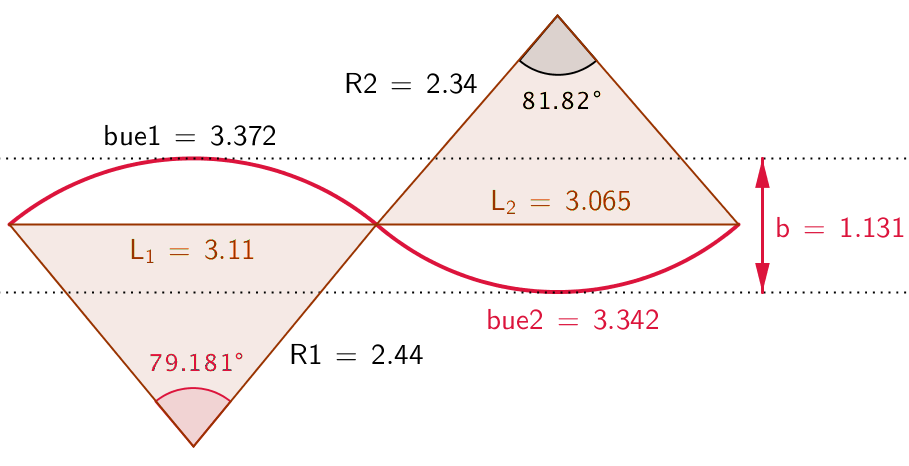
1. Vinkel u = 79,18°

2. Afstanden b = 1,131

3. Den samlede længde af muren = 3,342 + 3,372 = 6,714

4. Længden af muren i lige linje er 3,11 + 3,065 = 6,175.

   Den procentvise besparelse bliver: (2·6,175 m - 6,714 m)/(2·6,175 m) = 0,456 = 46 %

   Det er underforstået af højden af de to slags mure er den samme.

Løst i hånden:

1. Vinkel u målt i radianer = 3,372 m / 2,44 m = 1,382. Vinkel u målt i grader = 1,382·(180°/π) = 79,18°

2. Afstanden b er lig med summen af pilhøjderne og findes ved formlen:

   

3. Den højre buelængde bliver 2,34 m·(81,82°·π/180°) = 3.342 m. Den samlede længde af muren er 3,372 m + 3,342 m = 6,714

4. Længde af den tænkte lige mur er summen af korderne til de to cirkeludsnit:

   

   Den procentvise besparelse bliver som før: (2·6,175 m - 6,714 m)/(2·6,175 m) = 0,456 = 46 %

Svar på opgave 2 (Blomsterbed):

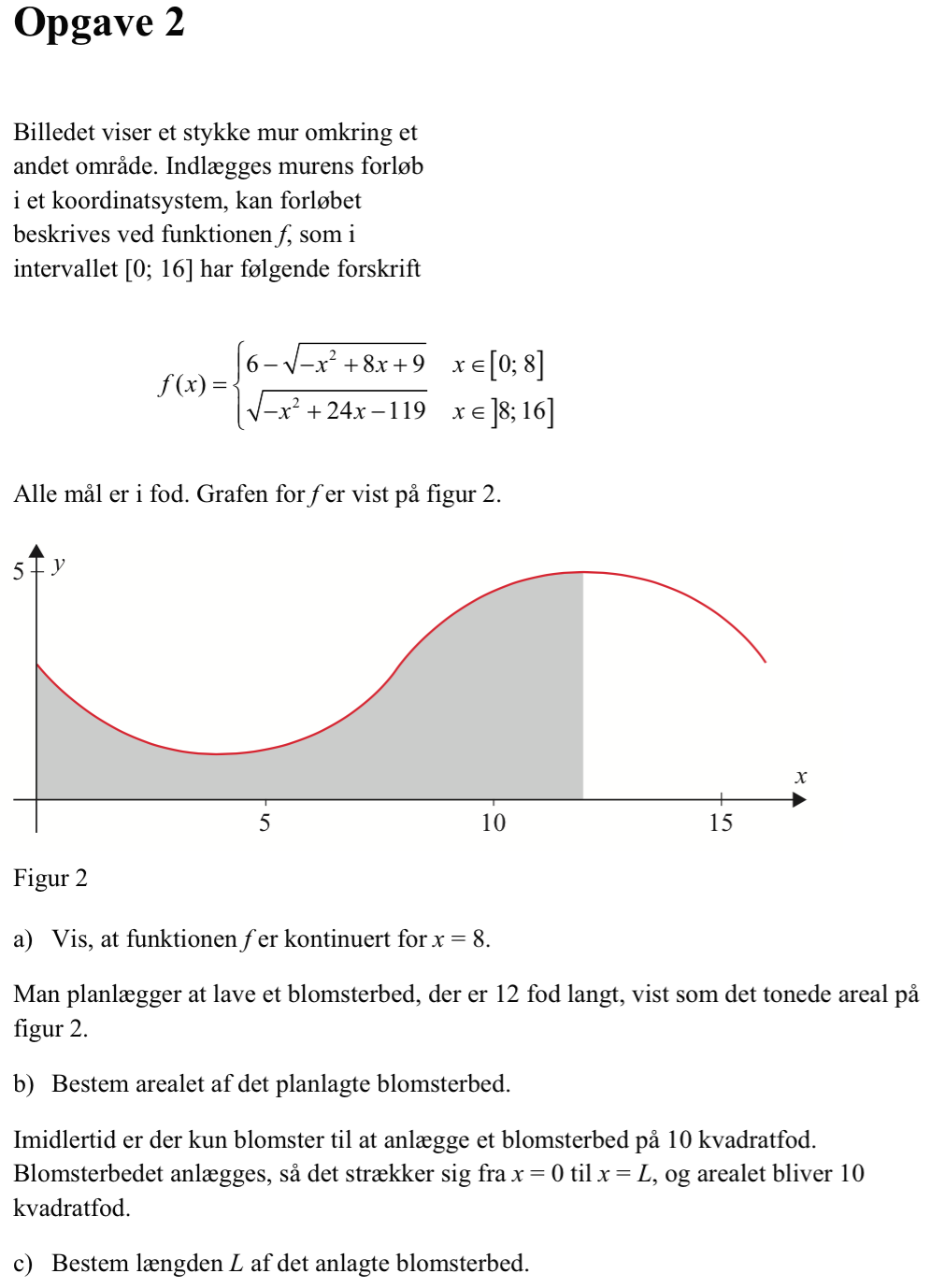
1. Man skal vise, at de to del-funktioner har samme grænseværdi for x gående mod 8. Dette vises ved indsættelse af x = 8:

   

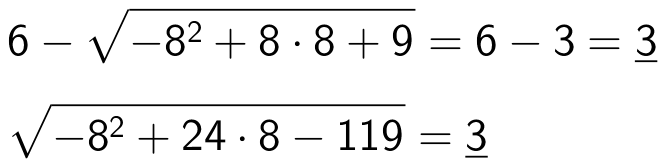
   Da grænseværdien er den samme for begge del-funktioner er f(x) kontinuert i x = 8.

2. Arealet er integralet af f(x) fra x = 0 til x = 12:

   

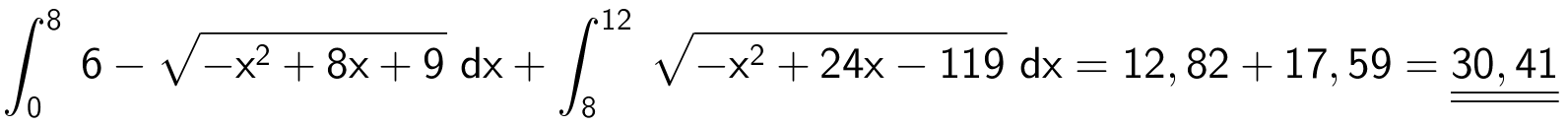
3. Arealet er integralet af f(x) fra x = 0 til x = 8 er 12,82 kvadratfod, som det fremgår af opgave b). Dvs. at L ligger mellem x = 0 og x = 8. Løsning i Ti-Nspire:

   

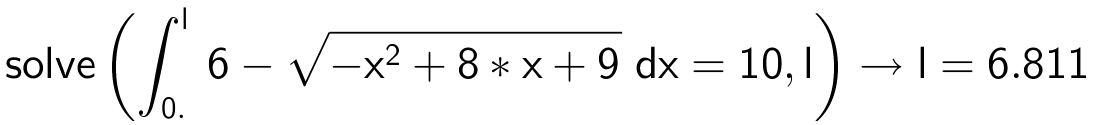
   Dvs. L = 6,81 fod

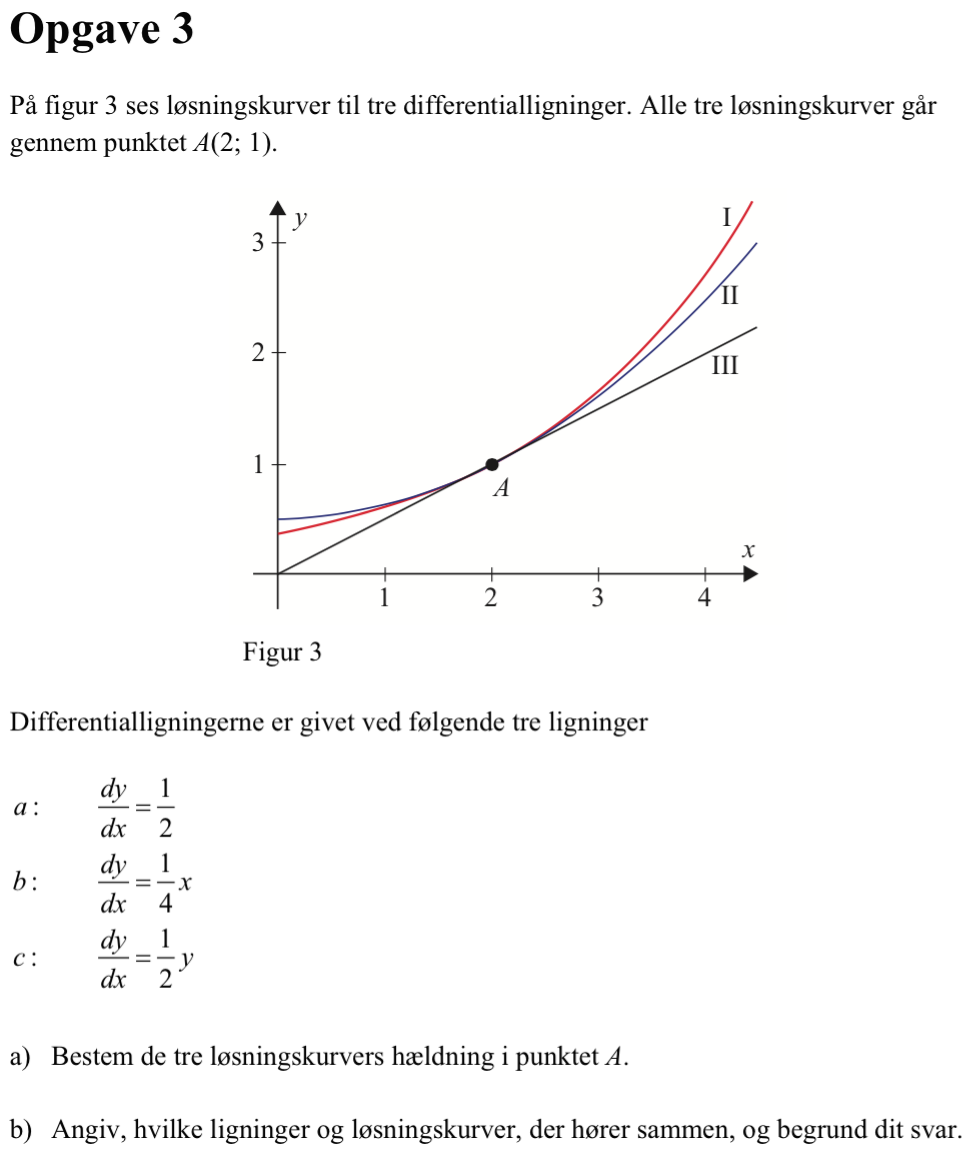
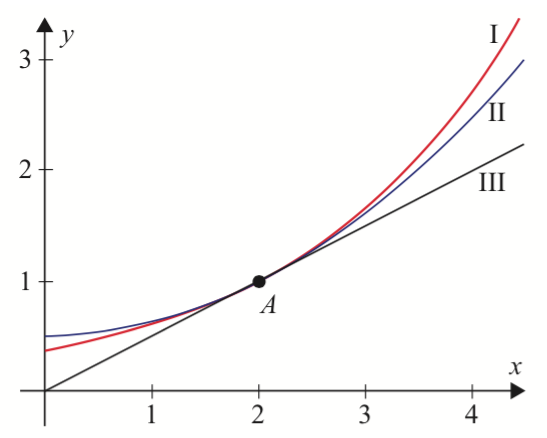
Svar på opgave 3 (Løsningskurver til differentialligninger):

1. Hældningen fås ved at indsætte (x,y) = (2,1) på højre side af differentialligningen (efter figuren at dømme er hældningerne ens).

   (a): hældning = 1/2 = 0,5

   (b): hældning = (1/4)·2 = 0,5

   (c): hældning = (1/2)·1 = 0,5

2. Man benytter, at dy/dx er hældningen til løsningskurven.

   Løsningskurven til (a) er en ret linje med hældningen 1/2, og svarer derfor til (III).

   Løsningskurven til (b) vokser for positive x og har hældningen 0 for x = 0. Det svarer til (II).

   Løsningskurven til (c) vokser for positive y. Den skærer y-aksen i y = ca. 0,3 og hældningen er en tilsvarende værdi. Det svarer til (I).

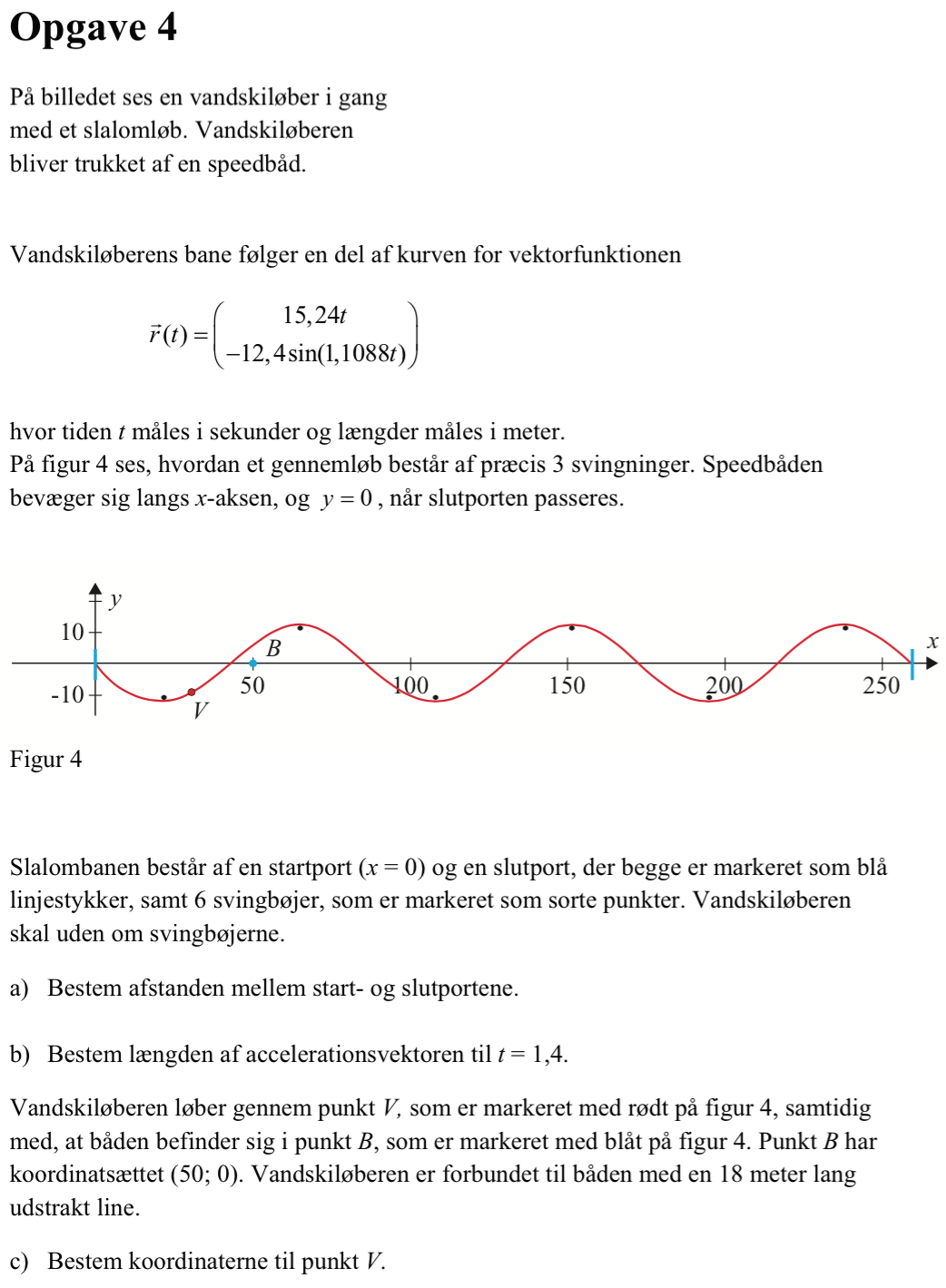
Svar på opgave 4 (Vandskiløber):

1. Man bruger i det følgende notationen r(t) er stedvektorfunktionen. Den tilhørende hastighedsvektorfunktion kaldes v(t), som er r(t)'. Den tilhørende accelerationsvektorfunktion kaldes a(t) = v(t)' = r(t)''.

   3 svingninger svarer til at 1,1088·t = 6π ⇒ t = 17,0 s. Længden af banen findes som x-koordinaten for r(t) når t = 17,0 s. Man får:

   Længde = 15,24·17,0 m = 259,1 m (passer med tegning).

2. Man skal finde |a(1,4s)|, dvs. længden af accelerationsvektoren til tiden 1,4 sekunder. Man har, at: a(t) = r(t)'' = (0; 15,246·sin(1,1088·t)).

   Længden af a(t) er lig med den numeriske værdi af y-koordinaten til accelerationsvektoren, da x-koordinaten til accelerationsvektoren er 0. Dermed får man at:

   |a(1,4s)| = |15,246·sin(1,1088·(1,4))| m/s² = 15,2 m/s²

3. Punktet V må ikke forveksles med hastighedsvektoren v(t). Punktet V er givet ved stedvektoren r(t) for et bestemt t, og dette t skal man finde.

   Man har vektoren VB = (50 - 15,24·t; -12,4·sin(1,1088·t)). Man skal finde det t, som gør at |VB| = 18. Dvs. man skal finde det tidspunkt, hvor længden af vektoren VB er 18.

   Dette løses i Ti-Nspire.

   Først oprettes vektor VB i Ti-Nspire:

   vb:=[50-15.24*t,−12.4*sin(1.1088*t)] ▸ [50-15.24*t,−12.4*sin(1.1088*t)]

   Dernæst bruges solve-kommandoen. I Ti-Nspire hedder længden af VB norm(VB).

   solve(norm(vb)=18,t) ▸ t=2.21724 or t=4.14244

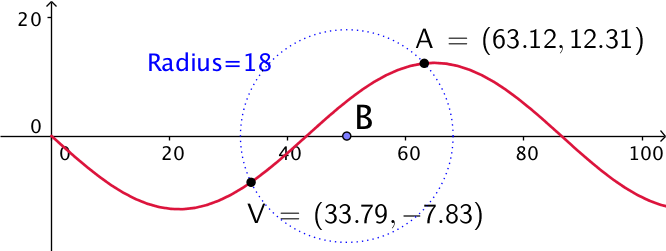
   Man skal nu finde ud af hvilket t, der er det rigtige. Man indsætter de to tidspunkter i r(t) og får:

   r(2.21724) ▸ [33.7907,−7.82705] og r(4.14244) ▸ [63.1308,12.3119]

   Det ses, at t=4,14244 s giver et koordinatsæt for V, hvor x-koordinaten er større end 50 m. Vi ved i følge tegningen, at den skal være mindre end 50 m. Dermed kan t = 4,14244 s ikke være løsningen.

   Dermed er V = r(2,217s) = (33,79m; −7,827m)

   Nedenunder er opgaven løst geometrisk i Geogebra (punktet A svarer til den falske løsning):

   

Svar på opgave 5 (Optimering af krukke):

1. (2): Indsættelse af formlerne for de enkelte del-overfladearealer

   (3): Reduktion af formel for overfladeareal

   (5): Indsættelse af formlerne for de enkelte del-volumener

   (6): Reduktion af formel for volumen

   (7): Udledning af formel for h som funktion af x når volumen er konstant 75 cm³ ud fra (6).

   (8): Indsættelse af udtryk for h fra (7) i formlen i (2).

   (9): Reduktion af (8)

2. Man skal differentiere A(x) fra a) og finde nulpunkter og fortegn for A'(x). Det gøres i Ti-Nspire:

   

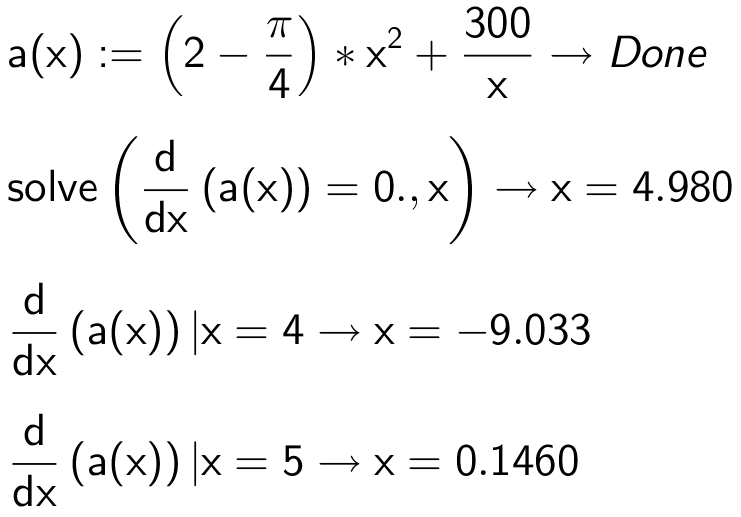
   Det ses at A(x) er aftagende før nulpunktet for A(x)' og voksende efter, dvs. at x = 4,980 cm er et minimum.

   Man får: x = 4,98 cm og h = 300/[(8 + π)·4,98²] cm = 1,09 cm

3. Det mindste areal er A(4,98). Det beregnes i Ti-Nspire: a(4.97988) → 90,36 cm²

Svar på opgave 6 (Pyramide):

1. Man skal finde længede af vektor AT. Man har, at AT = (1,1,3). Det giver: |AT| = √[1 + 1 + 9] = 3,32

2. Planens ligning findes ved hjælp af krydsproduktet af vektorerne AB=(2,0,0) og AT=(1,1,3). Ti-Nspire:

   crossP([1,1,3],[2,0,0]) ▸ [0,6,−2]

   Man tager skalarprodukttet af krydsproduktsvektoren og en vektor fra A, der ligger i planen, til (x,y,z), der er et vilkårligt punkt i planen. Ti-Nspire:

   dotP([0,−6,2],[x,y,z])=0 ▸ 2*z - 6*y = 0

   Forkortes det får man planens ligning: -3y + z= 0

3. Projektionerne findes i Ti-Nspire. For C får man :

   

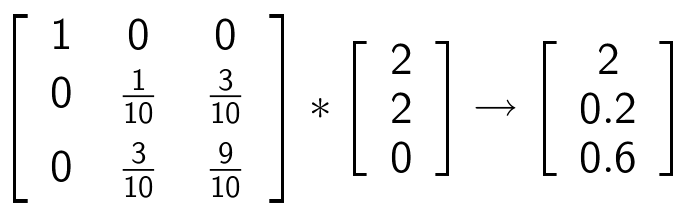
   For D får man

   

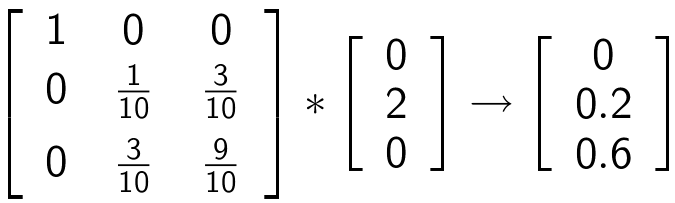
   Dvs. C' projektion på π er (2;0,2;0,6) og D's projektion er (0;0,2;0,6)

4. Ved rotation om x-aksen ændres x-koordinaterne ikke. Afstanden fra x-aksen til C og D er 2 i begge tilfælde. Man får

   C' = (2, 2·cos(25°), 2·sin(25°)) = (2, 1.813, 0.8452) og

   D' = (0, 2·cos(25°), 2·sin(25°)) = (0, 1.813, 0.8452)

5. Afbildningsmatricen bliver: