Svar på opgave 1:

Løst i Geogebra:

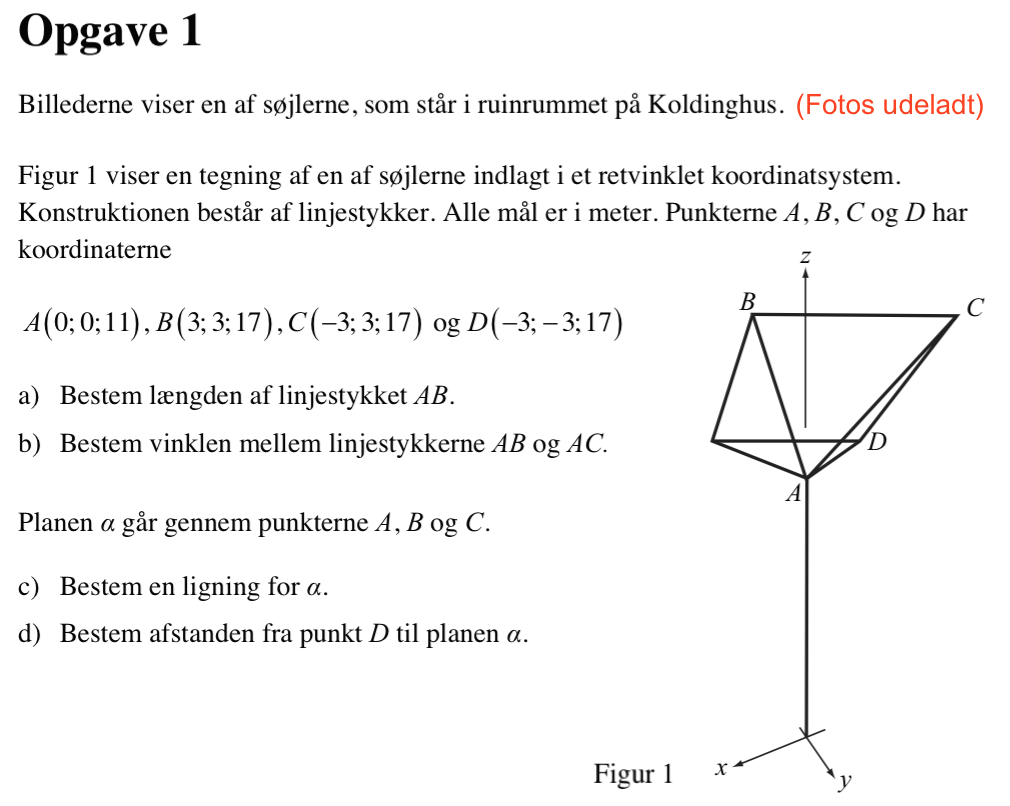
Man indsætter punkterne A, B, C og D i inputfeltet.

1. Man måler afstanden mellem A og B med afstands-værktøjet på menuen under vinkel-værktøjet. Dette giver længden af linjestykket AB = 7,348

2. Man opretter vektorerne AB og AC med vektor-værktøjet på menuen under linje-værktøjet. Vinklen mellem vektorerne måles med vinkel-værktøjet til 48,19°

3. Man bruger plan-gennem-tre-punkter værktøjet på punkterne A, B og C og finder ligningen for Alfa til: -2y + z = 11 eller: 2y - z + 11 = 0

4. Man opretter en ret linje gennem D og vinkelret på Alfa med vinkelret-linje værktøjet. Dernæst finder man skæringspunktet mellem denne linje og Alfa med skærings-værktøjet på menuen under punkt-værktøjet. Man måler afstanden mellem punkt D og skæringspunktet med længde-værktøjet. Denne afstand er afstanden mellem D og Alfa og måles til: 5,367

Løst i Ti-Nspire:

Man starter med at definere de fire punkter A, B, C og D som stedvektorer og dernæst vektorerne AB, AC og AD:

a:=[0,0,11] ▸ [0,0,11]

b:=[3,3,17] ▸ [3,3,17]

c:=[−3,3,17] ▸ [−3,3,17]

d:=[−3,−3,17] ▸ [−3,−3,17]

ab:=b-a ▸ [3,3,6]

ac:=c-a ▸ [−3,3,6]

ad:=d-a ▸ [−3,−3,6]

1. Længden af vektor AB findes ved hjælp af kommandoen norm():

   norm(ab*1.) ▸ 7.348

   Længden af AB er dermed 7,348

2. Man bruger kommandoen:

   

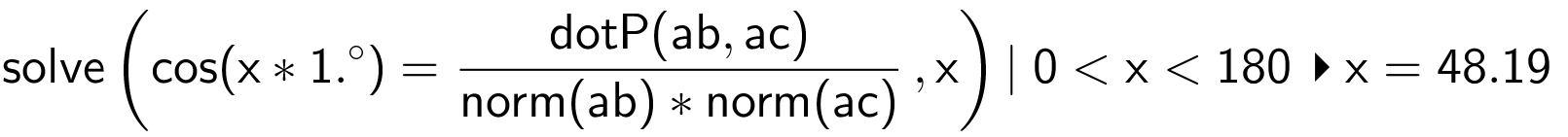
   Dette giver vinklen: 48,19°

3. Man skal have en normalvektor til planen. Man finder først krydsproduktet mellem vektor AB og vektor AC. Denne vektor kaldes normalv:

   normalv:=crossP(ab,ac) ▸ [0,−36,18]

   For at forenkle vektoren, divideres den igennem med det mindste hele tal forskellig fra 0, som er 18, og man får normalvektoren (0,−2,1).

   normalv:=normalv/18 ▸ [0,−2,1]

   Planens ligning findes ved hjælp af kommandoen:

   dotP(normalv,[x,y,z]-a)=0 ▸ −2*y+z-11=0

   Dvs. ligningen for alfa er 2y - z + 11 = 0,

   idet man ganger igennem med -1 for at få så få negative tal som muligt.

   I kommandoen benyttes at skalarproduktet mellem normalvektoren og en vektor fra punktet A til et vilkårligt andet punkt (x,y,z) i planen er 0.

4. Man bruger kommandoen:

   

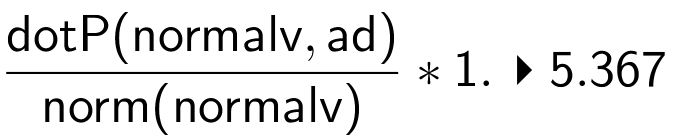
   Dvs. afstanden mellem D og Alfa er 5,367

   Formlen bygger på, at afstanden mellem Alfa og punktet D er lig med længden af projektionen af AD på en normalvektor til Alfa.

Svar på opgave 2:

1. Løsning i Ti-Nspire: Man opretter listerne:

   liste_x:={0,1,2,3} ▸ {0,1,2,3}

   liste_y:={1.806,4.433,9.588,22.52} ▸ {1.806,4.433,9.588,22.52}

   Man vælger kommandoen Statistik ▸ Statistiske beregninger ▸ Eksponetiel regression...

   Herefter vælger man de to lister man lige har oprettet. Man får resultatet:

   r² = 0.999, hvilket viser, at det er muligt at lave en regressionskurve, som passer godt med punkterne.

2. Beregningen fra a) giver at f(x) = 1.845·2.303^x

3. Man får i Ti-Nspire: f(0,5) = 2,80

4. Man finder de fire Lagrange-polynomier til:

   l₀(x) = (-1/6)·(x - 1)·(x - 2)·(x - 3)

   l₁(x) = (1/2)·x·(x - 2)·(x - 3)

   l₂(x) = (-1/2)·x·(x - 1)·(x - 3)

   l₃(x) = (1/6)·x·(x - 1)·(x - 2)

   Det interpolerede polynomium bliver:

   P(x) = l₀(x)·1,806 + l₁(x)·4,433 + l₂(x)·9,588 + l₃(x)·11,52 ⇒

   P(x) = 0,875·x³ - 1,361·x² + 3,112·x + 1,806

5. P(0,5) = 0,875·0,5³ - 1,361·0,5² + 3,112·0,5 + 1,806 = 3,132

   Denne værdi afviger 11% fra den, som man fandt med regressions-funktionen. Dvs. polynomiet passer ikke særlig godt i det område, man undersøger.

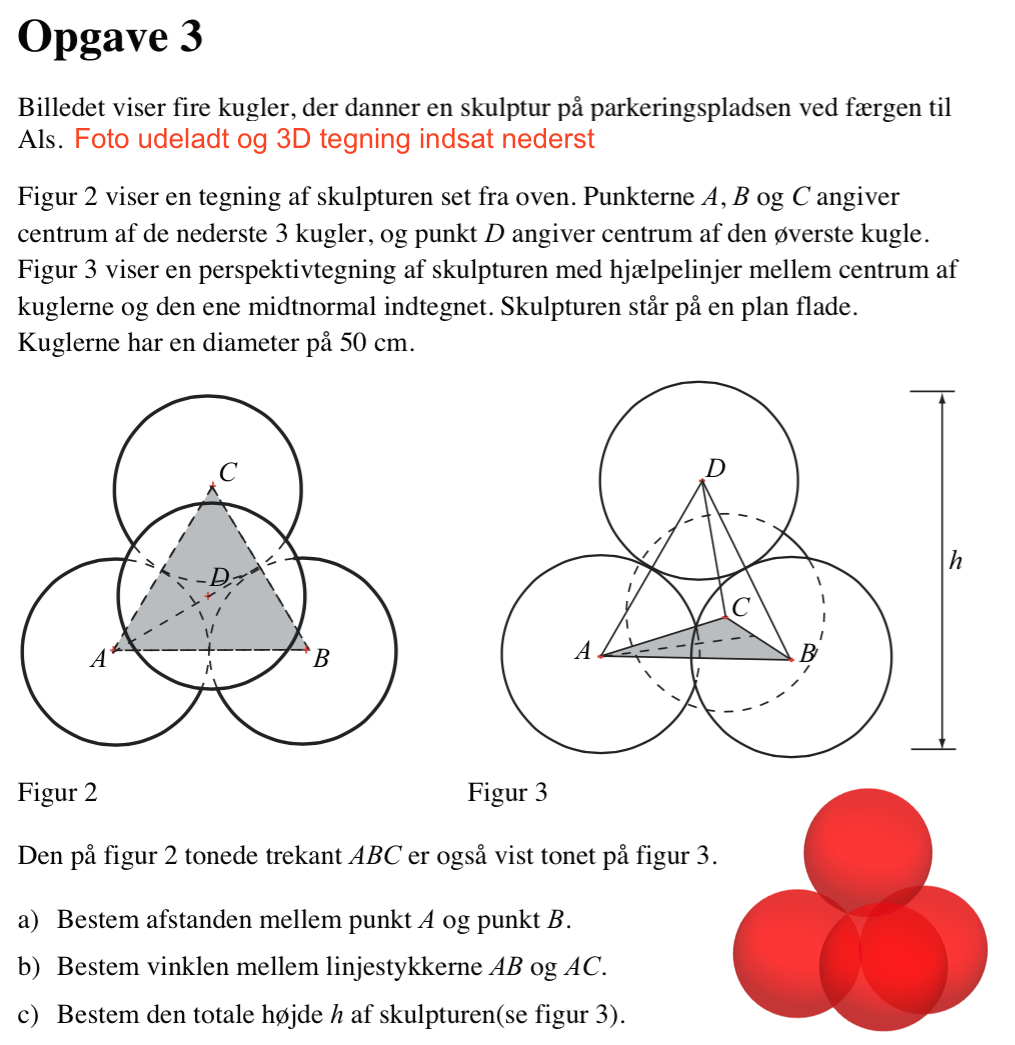
Svar på opgave 3:

1. Afstanden mellem A og B er 2 gange radius = diameter = 0,50 m

2. Trekant ABC er en ligesidet trekant og dermed er vinklen mellem AB og AC lig med 60 °

3. Den totale højde af skulpturen er 2 gannge radius af en kugle plus højden af tetraederen ABCD.

   Siden i tetraederen er 2·radius = 0,50 m som fundet i opgave a). Højden af tetraederen er (0,50 m)·(√2/√3) = 0.4082 m.

   Dermed bliver skulpturens samlede højde: 0,50 m + 0,4082 m = 0,908 m

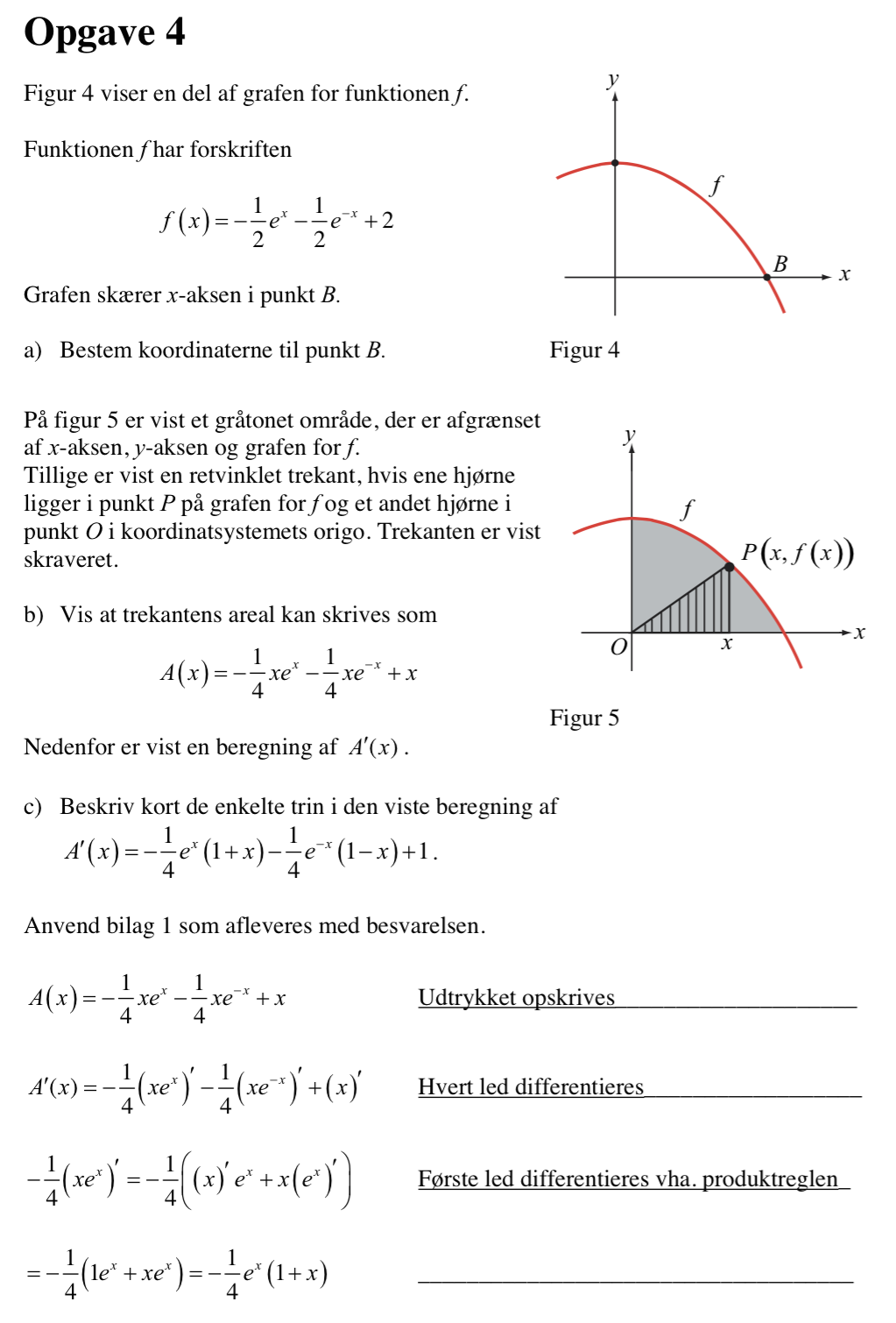
Svar på opgave 4:

1. B findes ved at løse ligningen f(x) = 0 med hensyn til x. Man bruger solve i Ti-Nspire

   solve((−1/2)*exp(x)-(1/2)*exp(−x)+2.=0,x)|x>0 ▸ x=1.31696

   Dvs. B = (1,317;0)

2. Trekantens areal er 0,5·højde·grundlinje = 0,5·f(x)·x =

   0,5·[(−1/2)*exp(x) - (1/2)*exp(−x) + 2]·x = [(−1/4)·exp(x) - (1/4)·exp(−x) + 1]·x =

   (−x/4)·exp(x) - (x/4)·exp(−x) + x, hvilke skulle bevises.

3. ...4) Differentiationen af første led gøres færdig og udtrykket reduceres.

   5) Andet led differentieres ved hjælp af produktreglen

   6) Differentiationen af første del af andet led

   7) Differentiationen af anden del af andet led

   8) Reduktion af andet led

   9) Differentiation af tredje led

   10) Færdiggørelse af udtryk ved at samle de tre led.

4. Man bruger fMax på formlen for A(x):

   fMax((−x/4)*exp(x)-(x/4)*exp(−x)+x,x)|0<x<1.317 ▸ x=0.7829

   Det x, som giver det største areal af trekanten, er 0,783

   Arealet af det grå område er integrafet af f(x) fra 0 til 1,317. Det findes til:

   integral((−1/2)*exp(x)-(1/2)*exp(−x)+2,x,0,1.317) ▸ 0.90186

   Arealet af den største trekant er A(0,7829) :

   (−x/4)*exp(x)-(x/4)*exp(−x)+x|x=0.783 ▸ 0.26523

   Dvs. trekanten udgør: (0,26523/0,90186)·100% = 29.4 % af det grå areal

5. Trapez-metoden giver følgende formel for arealet:

   

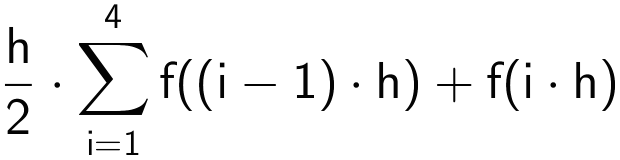
   hvor h = 1,317/4 = 0,32924. Dette løses i Ti-Nspire:

   f(x):=(−1/2)*exp(x)-(1/2)*exp(−x)+2. ▸ Udført (f(x) defineres)

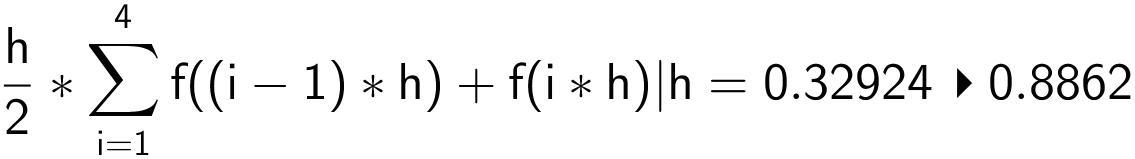   (summen beregnes)

   Arealet bliver ifølge metoden: 0,8862

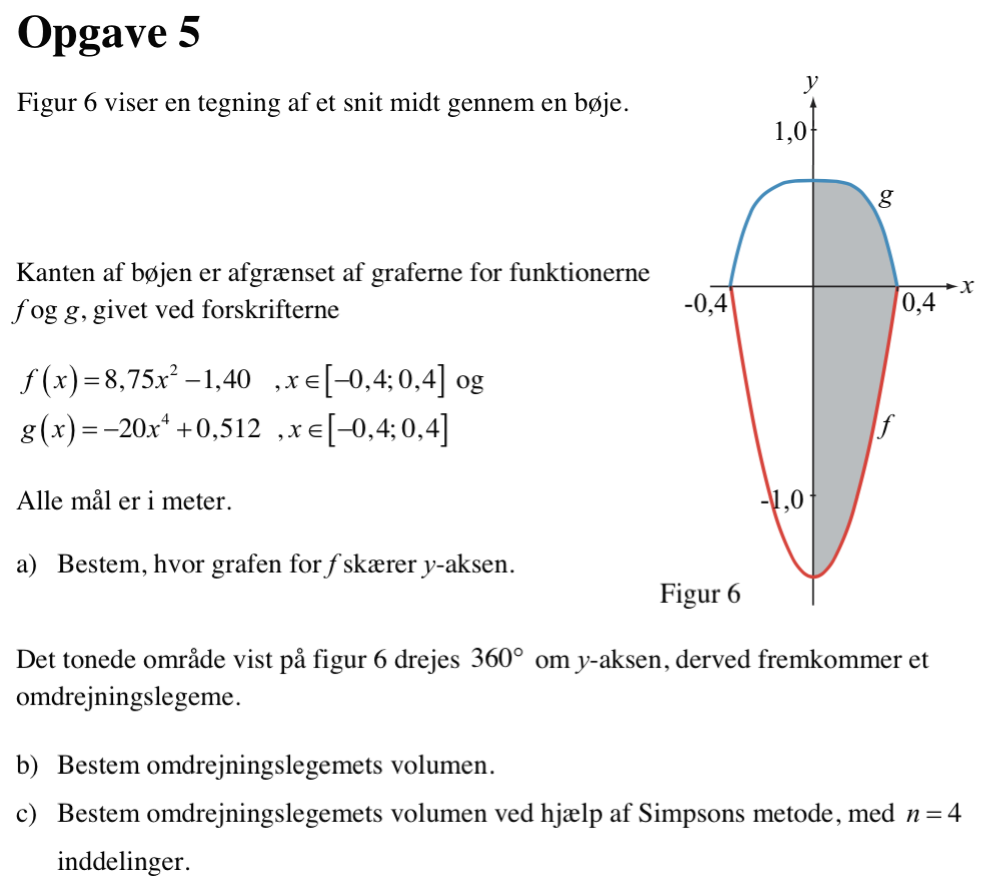
Svar på opgave 5:

1. Løst i Ti-Nspire:

   f(x):=8.75*x²-1.4 ▸ Udført (definer f(x))

   g(x):=-20x⁴+0.512 ▸ Udført (definer g(x))

   f(0) ▸ −1.4

   Dvs. f skærer y-aksen i y = -1,4

2. Formlen for volumen af omdrejningslegemet er:

   

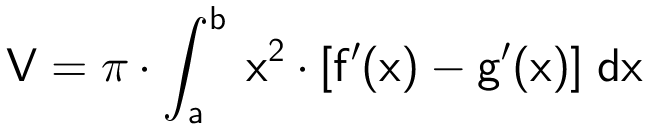
   hvor minustegnet foran g'(x) skyldes at g'(x) negativ i det interval, der integreres over. Man kalder integranden i volumenformlen for p(x) i Ti-Nspire:

   p(x):=x²*(derivative(f(x),x)-derivative(g(x),x)) ▸ Udført

   Volumenet beregnes:

   π*integral(p(x),x,0,0.4) ▸ 0.5234

   Dvs. volumenet af omdrejningslegemet er 0,523 m³

3. Simpson formel for n=4 giver:

   

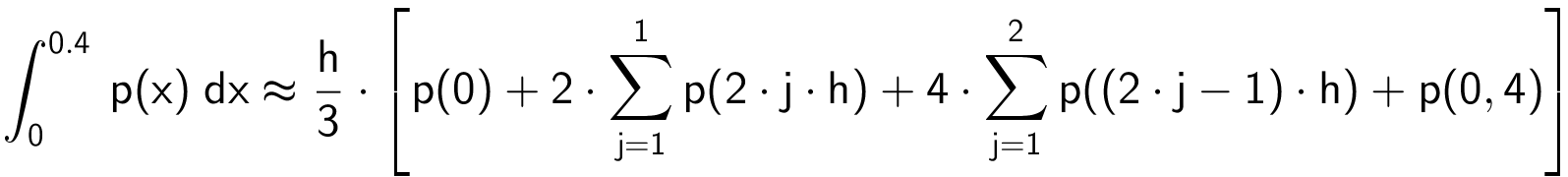
   hvor h er (b - a)/n = (0,4 - 0)/4 = 0,1. Dette beregnes i Ti-Nspire:

   

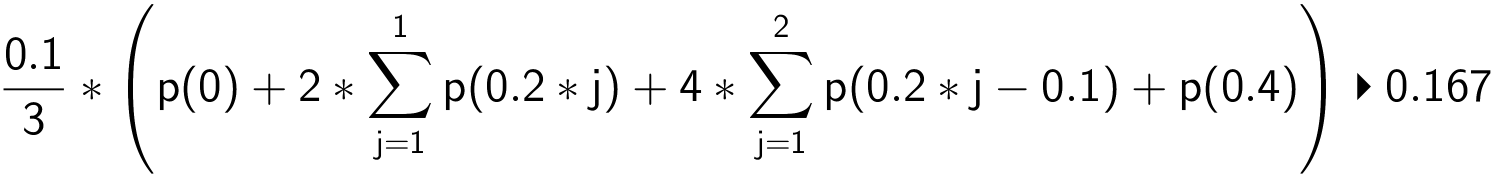
   Dette ganges med π og man får følgende volumen i følge Simpsons regel: 0,525 m³