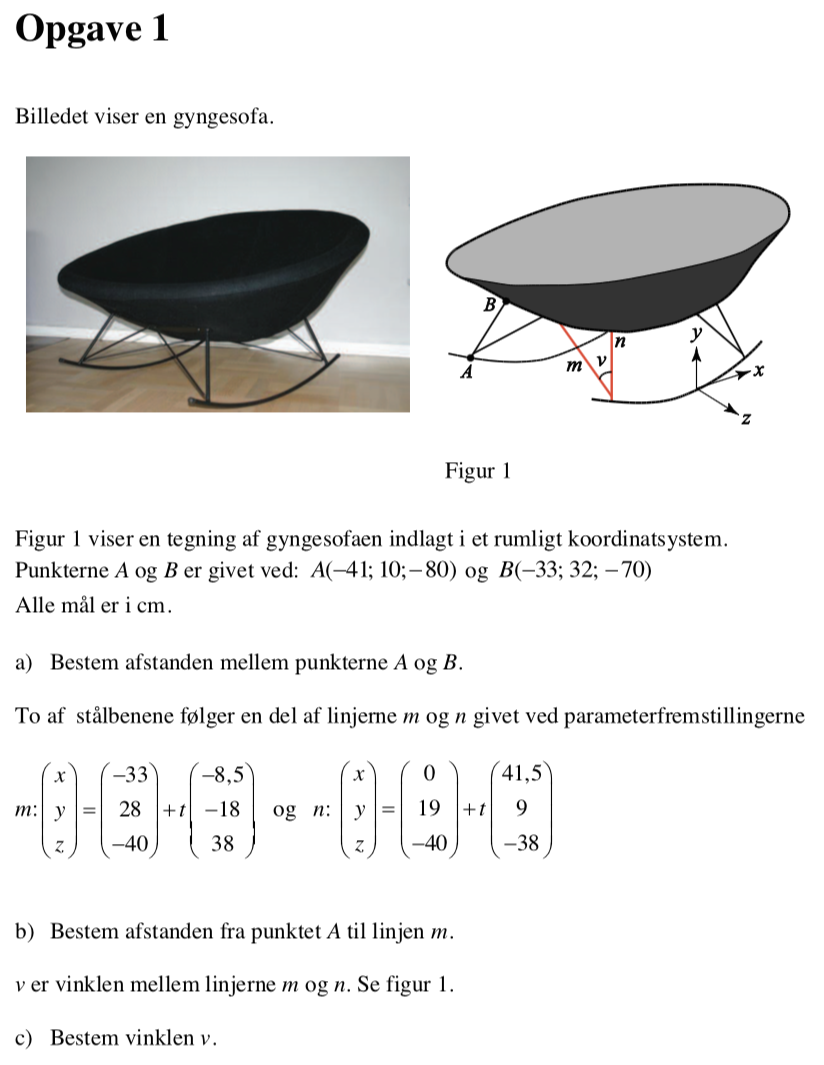
Svar på opgave 1:

Løst i Ti-Nspire.

1. Afstanden mellem A og B findes ved hjælp af afstandsformlen:

   √[(-33 - (-41))² + (32 - 10)² + (-70 - (-80))²] = √[8² + 22² + 10²] = 25,46

2. Man opretter punktet A som en stedvektor:

   a:=[−41,10,−80] ▸ [−41,10,−80]

   Man opretter linjen m:

   m(t):=[−33,28,−40]+t*[−8.5,−18,38] ▸ Udført

   Man finder det t, der giver det punkt P på linjen, som er nærmest A. Der gælder at PA·(−8.5,−18,38) = 0, hvor (−8.5,−18,38) er retningsvektoren for m. PA kan skrives som m(t)-a, hvor t skal findes. Man får t-værdien for P til:

   solve(dotP([−8.5,−18,38],m(t)-a)=0,t) ▸ t=−0.61296

   Dvs. stedvektoren til P kan skrives m(−0.61296). Vektoren PA kan derfor skrives:

   m(−0.61296) - a ▸ [13.21016,29.03328,16.70752]

   Man finder afstanden som længden af PA:

   norm([13.21016,29.03328,16.70752]) ▸ 36.008

   Dvs. afstanden mellem A og m er 36,01

3. m har retningsvektoren (−8,5;−18;38), mens n har retningsvektoren (41,5;9;−38). Man finder vinklen mellem m og n som vinklen mellem ders retningsvektorer. Det gøres med formlen for cos() til vinklen mellem to vektorer:

   solve(cos(x*1.°)=dotP([−8.5,−18,38],[41.5,9,−38])/(norm([−8.5,−18,38])*norm([41.5,9,−38])),x)|0<x<180 ▸ x=143.25

   Beregningen giver den stumpe vinkel mellem linjerne. Den spidse vinkel, som er den man søger, er 180° - 143,25° = 36,75°

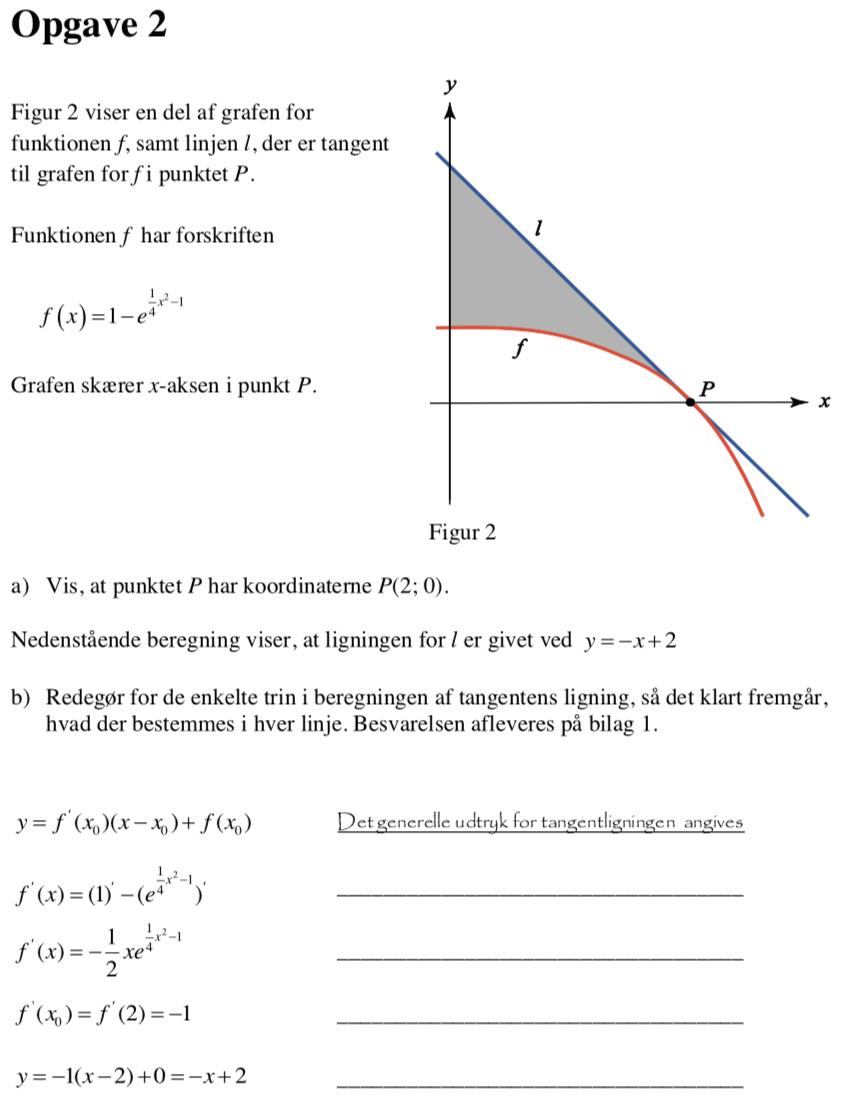
Svar på opgave 2:

1. Man skal vise, at f(2) = 0.

   Man får: f(2) = 1 - exp(0,25·2² - 1) = 1 - exp(1 - 1) = 1 - 1 = 0, hvilket skulle vises.

2. Man får

   

3. Kald forskriften for tangentens ligning for g(x).

   Arealet er integralet af g(x) - f(x). Det bregnes i Ti-Nspire til:

   Integral(−x+2-(1-exp((1/4)*x²-1)),x,0,2) ▸ 1.07616

   Dvs. arealet af det grå område er 1,076

4. Formlen for kurvelængden af f(x) fra x = 0 til x = 2 er

   

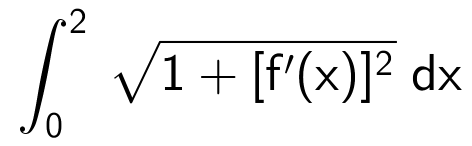
   Man opretter integraden som funktionen h(x) i Ti-Nspire:

   h(x):=sqrt(1+((−1/2)*x*exp((1/4)*x²-1))²)

   Simpsons regel med n = 2 giver, at kurvelængende kan tilnærmes til: (1/3)·(h(0) + 4·h(1) + h(2)) som i Ti-Nspire giver:

   (1./3)*(h(0)+4*h(1)+h(2)) ▸ 2.1748

   Dvs. kurvelængden er 2,17

Svar på opgave 3:

1. Årstal og løbstider oprettes som lister i Ti-Nspire:

   årstal:={1913,1923,1933,1943,1954,1965,1975,1985} ▸ {1913,1923,1933,1943,1954,1965,1975,1985}

   løbstid:={254.5,250.4,247.6,242.6,237.9,233.6,229.4,226.3} ▸ {254.5,250.4,247.6,242.6,237.9,233.6,229.4,226.3}

   Disse lister bruger man til at oprette et plot i Ti-Nspires Diagrammer og Statistik:

   

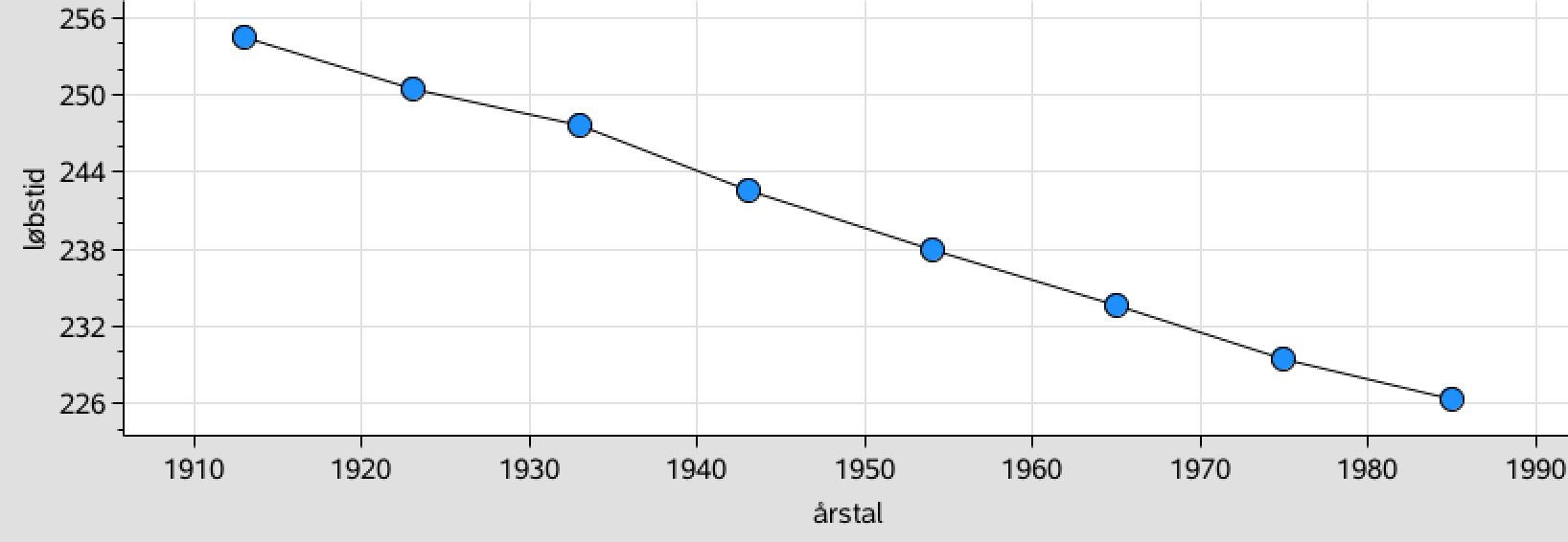
2. Man laver en lineær regression i Ti-Nspire (kommandoen ligger under menuen Statistik ▸ Statistiske beregninger ▸ Lineær regression...):

   LinRegMx årstal,løbstid,1: CopyVar stat.RegEqn,f1: stat.results ▸

   [["Titel","Lineær regression (mx+b)"]
   ["RegEqn","m*x+b"]
   ["m",−0.40094368340944]
   ["b",1021.6766210046]
   ["r²",0.99783598750226]
   ["r",−0.99891740774814]
   ["Resid","{...}"]]

   Af dette fremgår det, at a = -0,40 (kaldet "m" i Ti-Nspire) og b = 1022

3. Koefficienten a viser hvor meget rekorden forbedres hvert år. a = -0,4 viser, at den forbedres 0,4 sekunder hvert år.

4. Man skal beregne f(2015) som giver : −0,401·2015 + 1022 sekunder = 214 sekunder214 sekunder

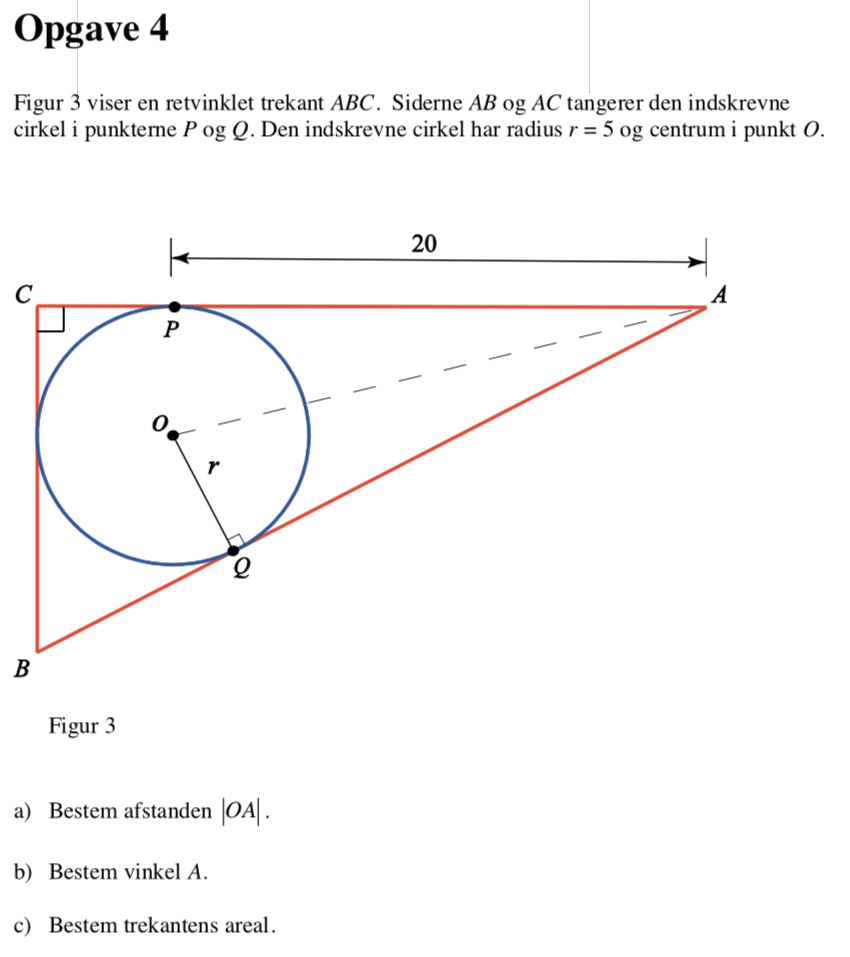
Svar på opgave 4:

1. Punkterne OQA danner en retvinklet trekant, hvor |OA| kan findes ved hjælp af Pythagoras læresætning. Man får:

   |OA|² = r² + 20² ⇒

   |OA|² = 5² + 20² ⇒

   |OA|² = 425 ⇒

   |OA| = √425 = 20,62

2. Der gælder at tan(0,5·∠A) = r/20 ⇒

   tan(0,5·∠A) = 5/20 ⇒

   tan(0,5·∠A) = 1/4 ⇒

   0,5·∠A = tan^-1(1/4) ⇒

   ∠A = 2·tan^-1(1/4) ⇒

   ∠A = 28,1°

3. Trekant ACB er retvinklet. Der gælder at trekantens areal er 0,5·|AC|·|BC|.

   Der gælder også, at |BC|/|AC| = tan(∠A) ⇒ |BC| = |AC|·tan(∠A).

   Det giver tilsammen, at arealet = 0,5·|AC|·|BC| = 0,5·|AC|·|AC|·tan(∠A) = 0,5·|AC|²·tan(∠).

   |AC| = 20 + r = 20 + 5 = 25. Dermed bliver arealet af ABC:

   0,5·|AC|²·tan(∠) = 0,5·25²·tan(28,1°) = 166,86

Svar på opgave 5:

1. Man skal løse ligningen f(x) = 0 med hensyn til x og får:

   solve(−sqrt(32.5²-x²)+12.5=0,x) ▸ x=−30. or x=30.

   Dvs. grafen skærer x-aksen for x = -30 og for x = 30

2. Rumfanget af bunden af grillen kan bestemmes på to måder. Entens som rumfanget af et omdrejningslegeme eller som rumfanget af en kuglekalot.

   Med formlen for et omdrejningslegeme roteret omkring y-aksen får man i Ti-Nspire:

   Integral(abs(2*π*x*f(x)),x,0,30) ▸ 32463.1

   For at bruge formlen for rumfanget af en kuglekalot bemærker man, at kuglekalotten har en højde på 20 (32,5 - 12,5), og at radius af dens grundflade er 30. Det giver rumfanget beregnet i Ti-Nspire:

   (π/6.)*20*(3*30²+20²) ▸ 32463.1

   Dvs. bunden af grillen har rumfanget = 32.463 cm³

3. Man skal opstille Lagragepolynomiet gennem punkterne:

   x₀ = -28, f(x₀) = -4

   x₁ = 0, f(x₁) = 20

   x₂ = 28, f(x₂) = -4

   Man får del-polynomierne:

   L₀(x) = 4·[(x-0)/(−28-0)]·[(x-28)/(−28-28)] = -x²/392 + x/14

   L₁(x) = −20·[(x-(−28))/(0-(−28))]·[(x-28)/(0-28)] = 5·x²/196 - 20

   L₂(x) = −4·[(x-(−28))/(28-(−28))]·[(x-0)/(28-0)] = −x²/392 - x/14

   Dette giver det samlede Lagrangepolynomium: P₂(x) = L₀(x) + L₁(x) + L₂(x) = x²/49 - 20

Svar på opgave 6:

1. Højden er y-værdien til r(0), som er -4,91·0² + 30·0 + 0,95 m = 0,95 m

2. Vinklen findes ud fra hastighedsvektoren v(t) for pilen.

   v(t) = r'(t) = (25;-9,82·t + 30).

   Hastighedsvektoren i t=0 er v(0) = (25;30). Vinklen α mellem denne vektor og vandret findes ved formlen: tan(α) = 30/25 = 6/5. Denne ligning løses med hensyn til α i Ti-Nspire:

   solve(tan(x*1.°)=6/5,x)|0<x<90 ▸ x=50.19

3. Man kan besvare opgaven ved at finde den mindste afstand mellem pil og abe. Man opretter de to vektorfunktioner i Ti-Nspire:

   p(t):=[25*t,−4.91*t²+30*t+0.95] ▸ Udført

   q(t):=[8,−4.91*t²+12] ▸ Udført

   Afstanden mellen dem findes som længden af vektoren q(t) - p(t). Denne længde beregnes i Ti-Nspire med kommandoen:

   afstand(t):=norm(p(t)-q(t)) ▸ Udført

   Man finder derefter den t-værdi, der giver mindste værdi af afstanden ved hjælp af fMin() kommandoen:

   fMin(afstand(t),t) ▸ t=0.3485

   Denne t-værdi indsættes i afstands-udtrykket for at finde minimums-afstanden:

   afstand(t=0.3485) ▸ 39.05*√(t²-0.6970*t+0.1220)=0.9283

   Det ses at den mindste afstand er 0,93 meter, og derfor gælder at pilen ikke rammer aben.