
Svar på opgave 1:
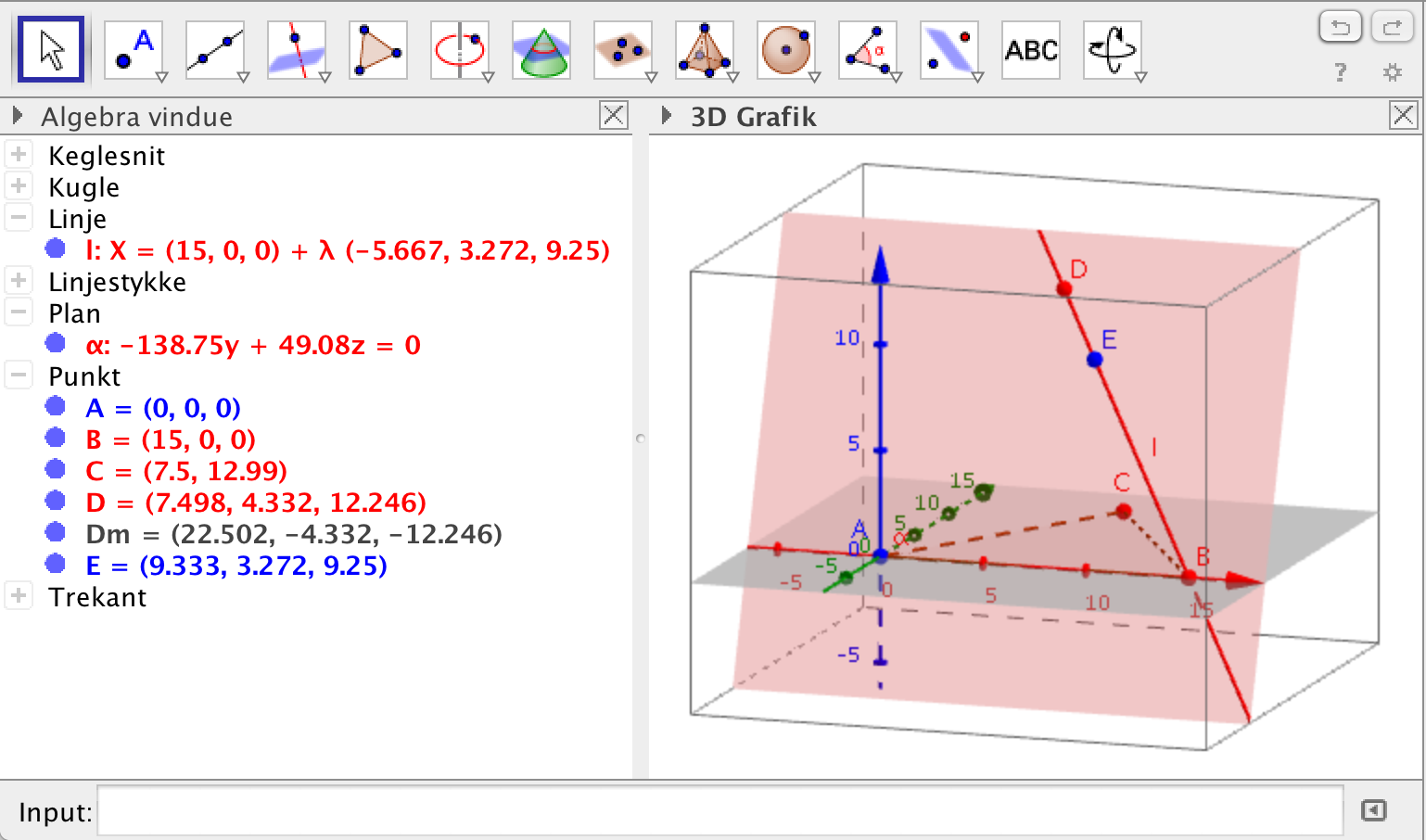
Løsning i Geogebra.
-
Løst i hånden:
B befinder sig på x-aksen i en afstand af 15 fra A. Dermed er B's koordinater (15,0,0).
C er et af hjørnerne i den ligesidede trekant ABC. x-koordinaten for C bliver halvdelen af 15, da højde er lig med median for alle hjørner af den ligesidede trekant. y-koordinaten til C er lig med højden i den ligesidede trekant, som er (15/2)·√3 = 12,99.
C bliver dermed: (7,5;12,99;0)
-
Løst i hånden:
Linjen gennem B og E kaldes l. B ligger på l og vektoren BE er retningsvektor for linjen. BE = (9,333 - 15;3,272;9,25) = (-5,667;3,272;9,250)
Parameterfremstillingen bliver l: (x,y,z) = (15,0,0) + t·(-5,667;3,272;9,250), t∈R.
I Geogebra:
Man vælger linjeværktøjet og trykker på B og E. Derved fremkommer parameterfremstillingen for l, som ses på billedet, hvor λ er parameter.
-
I Geogebra vælger man værktøjet plan-gennem-tre-punkter og klikker på A-B-E. Der ved fremkommer planens ligning: -138,75y + 49,08z = 0 eller forkortet: 2,827y - z = 0
-
I Geogebra findes D ved at afsætte en kugle (ikke vist på tegningen) omkring B med radius 15. Der hvor kuglen skærer linjen l er D. Skæringspunktet findes ved hjælp af skæringsværktøjet.
D aflæses til (7,497;4.332;12,25)
Løsning i Ti-Nspire.
-
Som ovenfor.
-
Som ovenfor.
-
Man opretter vektorerne AB = (15,0,0) og AE = (9,333;3,272;9,250). Dernæst finder man deres krydsprodukt, som er en normalvektor for den plan, der indeholder A, B og E. Normalvektoren kaldes n.
n:=crossP(ab,be) ▸ [0.,−138.75,49.08]
Man opretter en vektor fra A til punktet P = (x,y,z) et tilfældigt punkt i rummet. Der gælder, at for de punkter (x,y,z), der ligger i planen, der indeholder A, B og E, er skalarproduktet af vektor AP og n lig med 0. Det giver planens ligning:
dotP(n,ap)=0 ▸ 1.000*z-2.827*y=0
Dvs. planens ligning er z - 2,827y = 0 eller 2,827y - z= 0
-
Man finder det t som giver et punkt på l, der befinder sig i afstanden 15 fra B i BE's retning.
Længden af BE findes i Ti-Nspire: norm(be) ▸ 11.331.
Den t værdi, der giver t·|BE| = 15, er t = 15/11,331 = 1,3238. Denne værdi af t indsættes i ligningen for l og man får
[15,0,0]+1.324*[−5.667,3.272,9.25] ▸ [7.4969,4.3321,12.247]
Dvs. D = (7,497;4.332;12,25)

Svar på opgave 2:
Løst i Ti-Nspire.
-
Man opretter to lister, en for koncentrationen kaldet cl og en for hastigheden kaldet vl:
cl:={0.01,0.015,0.02,0.03,0.05} ▸ {0.01,0.015,0.02,0.03,0.05}
vl:={33.,74.25,132.,297.,825.} ▸ {33.,74.25,132.,297.,825.}
Man laver en potensregression på de to lister. Man finder kommandoen under menuen Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Potensregression...:
PowerReg cl,vl,1: CopyVar stat.RegEqn,f1: stat.results ▸
[["Titel","Potensregression"]
["RegEqn","a*x^b"]
["a",329999.99999999]
["b",2.]
["r²",1.]
["r",1.]
["Resid","{...}"]
["ResidTrans","{...}"]]Det ses, at r2 = 1, dvs. forklaringsgraden er 100 %, og dermed kan funktionen betragtes som en potensfunktion.
-
Potensregressionen er her givet på formen a*x^b, dvs. a svarer til k i opgaven og b svarer til n. Man får resultatet: k = 330.000 μM-1s-1 og n = 2
-
Man løser differentialligningen med desolve-kommandoen:
deSolve(c'+25*c=0.1 and c(0)=0.1,t,c) ▸ c=0.096*e−25*t+0.004
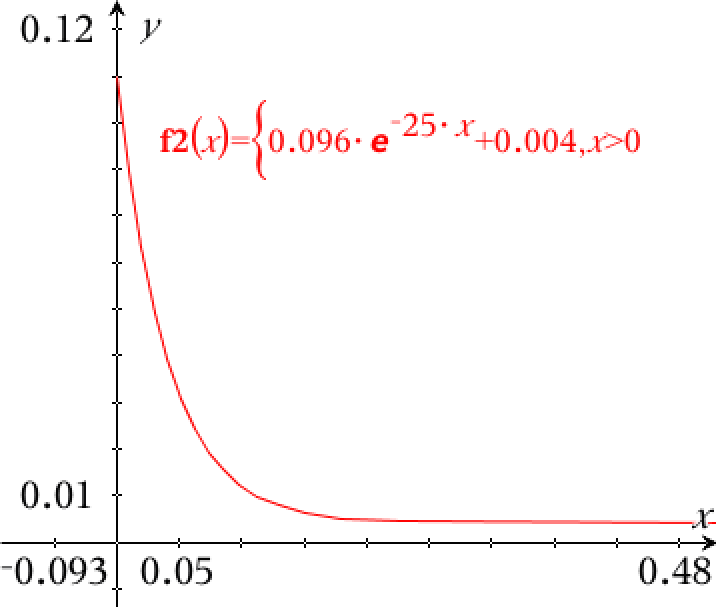
Dvs. løsningen er c(t) = 0,096·e−25t + 0,004 M
-
Grafen er tegnet nedenfor i Ti-Nspire.
-
Tidspunktet findes i Ti-Nspire ved hjælp af solve-kommandoen:
solve(0.096*e−25*t+0.004=0.05,t) ▸ t=0.029428
Dvs. koncentrationen bliver 0,05 M efter 0,029 sekunder
Svar på opgave 3:
Løst i Ti-Nspire.
-
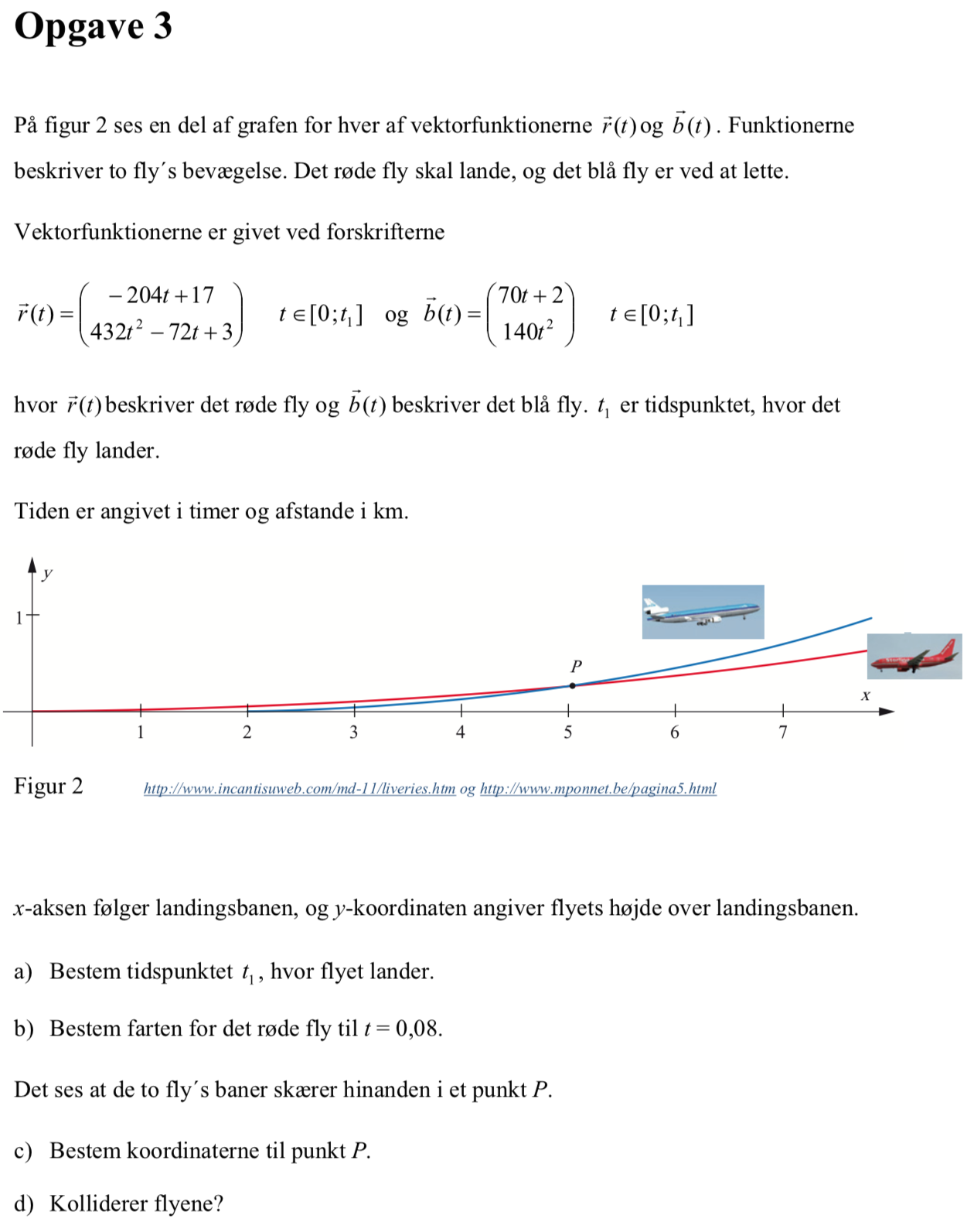
Man skal finde det tidspunkt, hvor y-værdien af r(t) er lig med 0. Man får
solve(432*t^(2)-72*t+3=0.,t) ▸ t=0.08333
Dvs. t1 = 0,0833 timer = 5 minutter
-
Hastighedsvektoren for det røde fly kaldes vr(t) og er lig med r'(t). Det giver:
vr(t):=[derivative(−204*t+17,t),derivative(432*t^(2)-72*t+3,t)] ▸ Udført
Farten af det røde fly til tiden 0,08 timer er længden af hastighedsvektoren til t=0,08. Længden af vektoren findes ved hjælp af norm()-kommandoen. Man får:
norm(vr(0.08)) ▸ 204.02
Dvs. det røde flys fart til tiden 0,08 timer er 204 km/t
-
Det bemærkes, at de to fly ikke nødvendigvis når punktet til samme tidspunkt. Man giver de to stedfunktioner hver sin parameter (t for det røde fly og s for det blå) og sætter deres x-værdier henholdsvis deres y-værdier lig med hinanden. Man bruger solve-kommandoen til at finde s og t:
solve(−204.*t+17=70*s+2 and 432*t2-72*t+3=140*s2,s,t)|s>0 and t>0 ▸ s=0.04335 and t=0.05865
Man finder punktet ved at indsætte t = 0,05865 i r(t):
r(0.058653) ▸ [5.0348,0.2631]
Dvs. punktet P er (5,03 km;0,263 km)
-
De kolliderer ikke, da de ikke når punktet P til samme tidspunkt (s ≠ t i forrige opgave).
Svar på opgave 4:
Løst i Ti-Nspire.
-
Man opretter r(x):
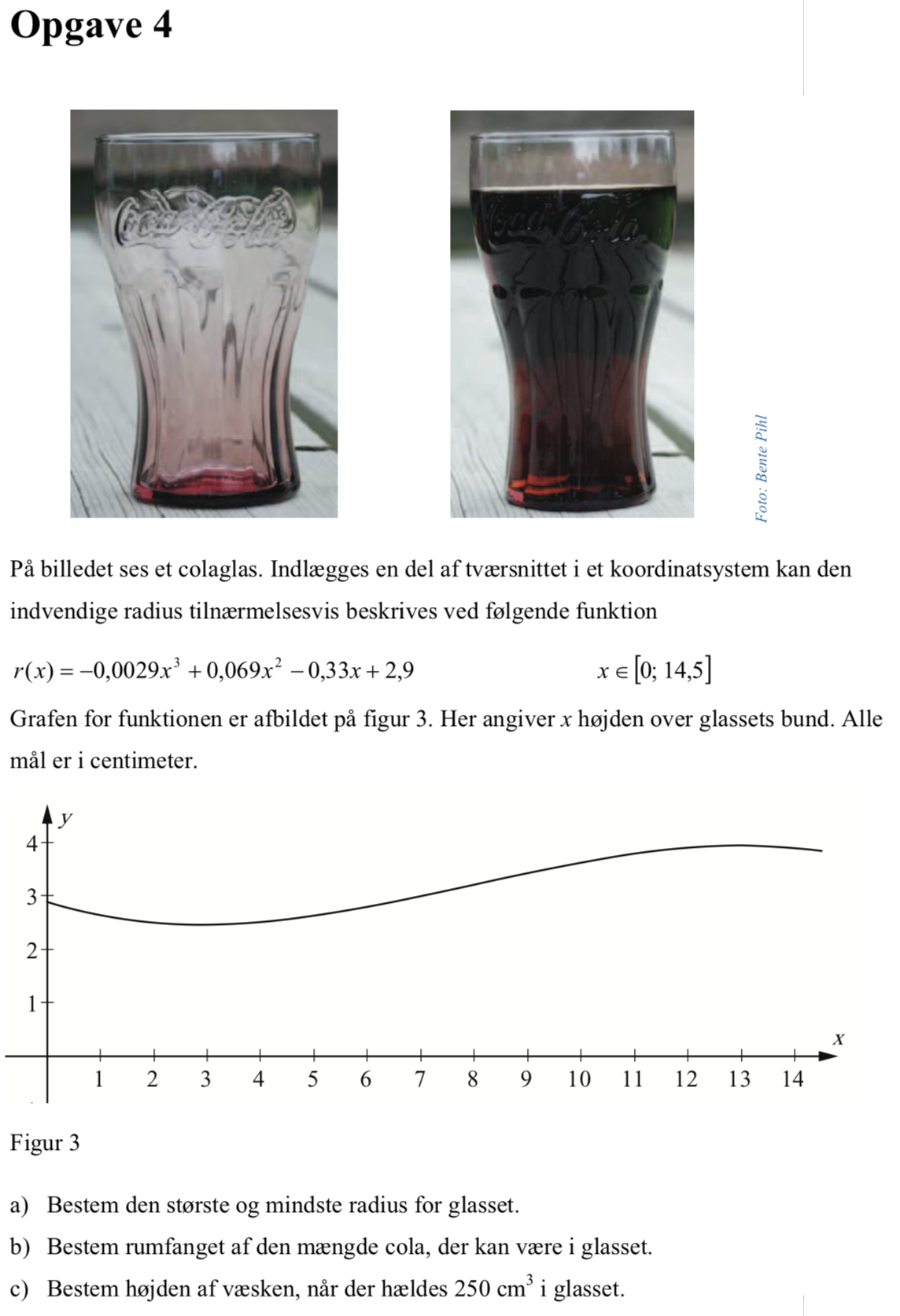
r(x):=−0.0029*x3+0.069*x2-0.33*x+2.9 ▸ Udført
Det x, der giver den mindste værdi, findes med fMin()-kommandoen (man husker at indsætte grænserne for x):
fMin(r(x),x)|0≤x≤14.5 ▸ x=2.934
Dette indsættes i r(x) for at finde mindsteværdien:
r(2.93401) ▸ 2.4525
Den største værdi findes med fMax()-kommandoen og r(x):
fMax(r(x),x)|0≤x≤14.5 ▸ x=12.928
r(12.928) ▸ 3.8999
Dvs. mindste-værdien er 2,453 og største-værdien er 3,900
-
Man skal bestemme rumfanget af det legeme, der fremkommer ved at dreje r(x) 360° omkring x-aksen. Man får:
Integral(π*(r(x))2,x,0,14.5) ▸ 460.63
Dvs. glassets rumfang er 461 cm3
-
Man skal finde højden h, så h, når det bliver indsat som øvre grænse i formlen for rumfanget, giver rumfanget 250. Man får:
solve(Integral(π*(r(x))2,x,0,h)=250,h) ▸ h=9.8885
Dvs. højden af 250 ml væske i glasset er 9,9 cm

Svar på opgave 5:

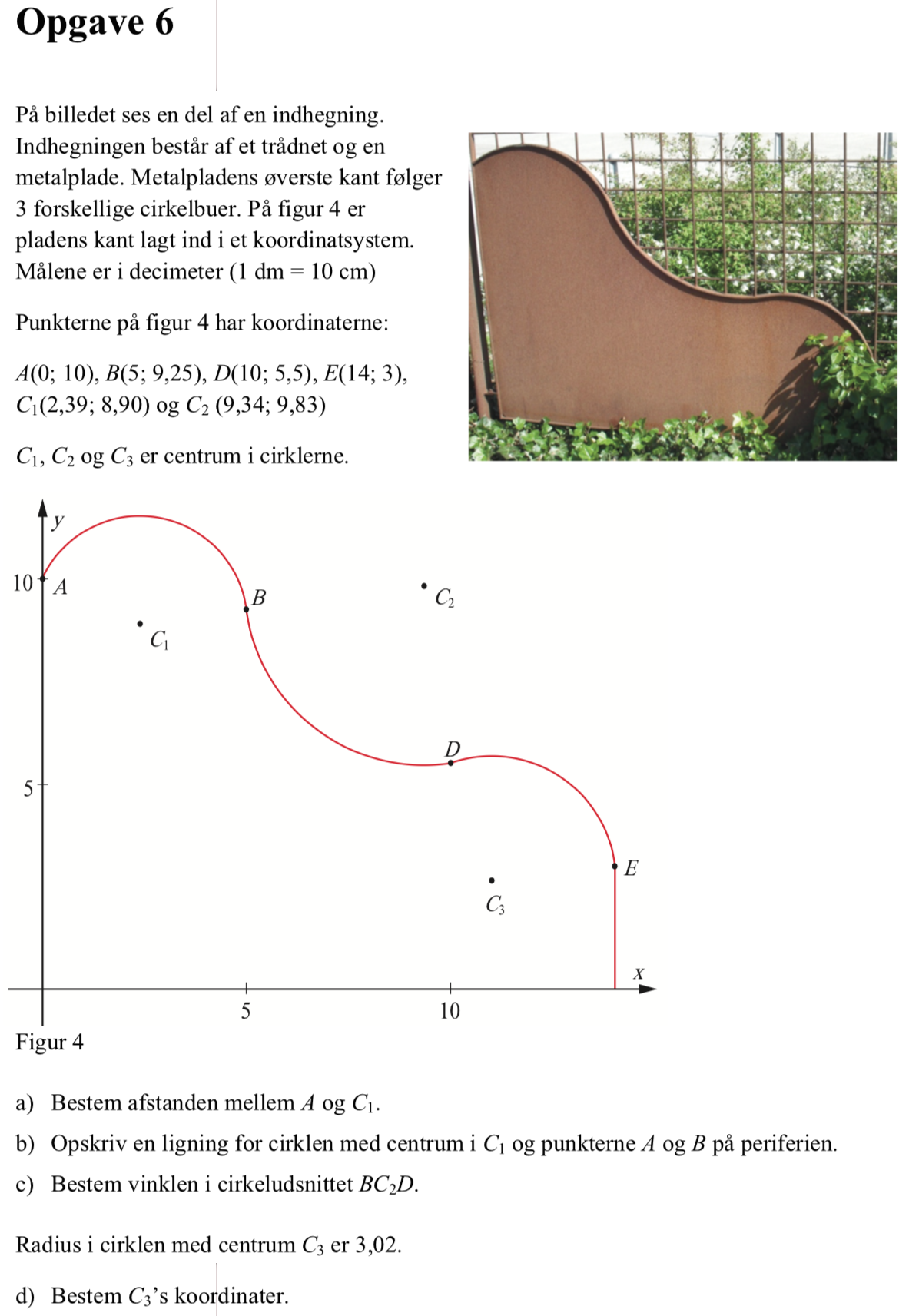
Svar på opgave 6:
Løst i Ti-Nspire.
-
Man finder afstanden som længden af vektoren AC1 ved hjælp af norm()-kommandoen:
norm([2.39,8.9]-[0,10]) ▸ 2.63099
Dvs. afstanden mellem A og C1 er 2,63 dm
-
Cirklen har C1 = (2,39;8,90) som centrum og radius = |AC1| = 2,631. Man får cirklens ligning:
(x - 2,39)2 + (y - 8,90)2 = 2,6312
-
Vinklen findes som vinklen mellem vektorerne C2B = (5;9,25) - (9,34;9,83) = (−4,34;−0,58) og C2D = (10;5,5) - (9,34;9,83) = (0,66;−4,33). Det gøres ved hjælp af formlen mellem to vektorer:
solve(cos(x*1.°)=dotP([−4.34,−0.58],[0.66,−4.33])/(norm([−4.34,−0.58])*norm([0.66,−4.33])),x)|0<x<180 ▸ x=91.055
Vinklen af cirkeludsnittet BC2D er dermed 91,6°
-
Tegning i Geogebra.
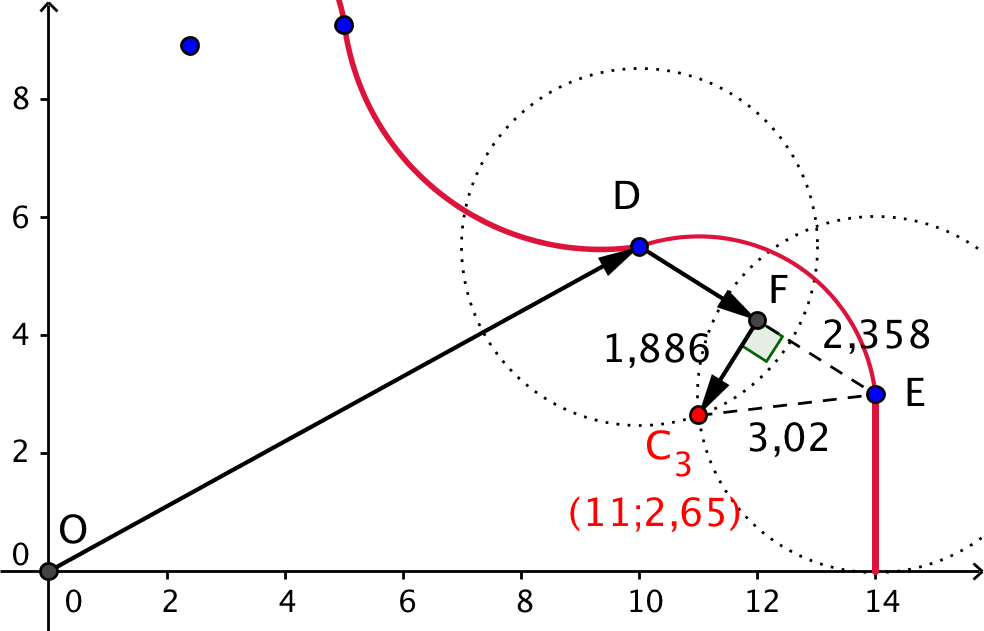
Løsningen på tegningen er lavet ved at afsætte to cirkler med radius 3,02 ud fra henholdsvis D og E. Det nederste venstre skæringspunkt mellem de to cirkler er C3. Koordianterne til punktet aflæses til (11;2,65).
Løsning med vektorer (med henvisning til ovenstående tegning):
Sæt O = (0,0) og midtpunktet mellem D og E til F. Stedvektoren til C3 kan findes som OD + DF + FC3· DF = 0,5·DE = (2;−1,25). FC3 findes som minus enheds-tværvektoren til DF gange |FC3|.
Denne længde findes som den mindste katete i den retvinklede trekant FEC3. Ved hjælp af Pythagoras læresætning fås: |FC3| = √[3,022 - (0,5·|DE|)2] = √[3,022 - 2,3582] = 1,886.
DE = (4;-2,5). Enheds-tværvektoren til DE er (-2,5;-4)/|DE| = (-2,5;-4)/[√(2,52 + 42)] = (−0,53;-0,848).
OC3 = (10;5,5) + (2;−1,25) + (−0,53;-0,848)·1,886 = (11,0;2,65)
Dvs. C3 = (11,0;2,65)