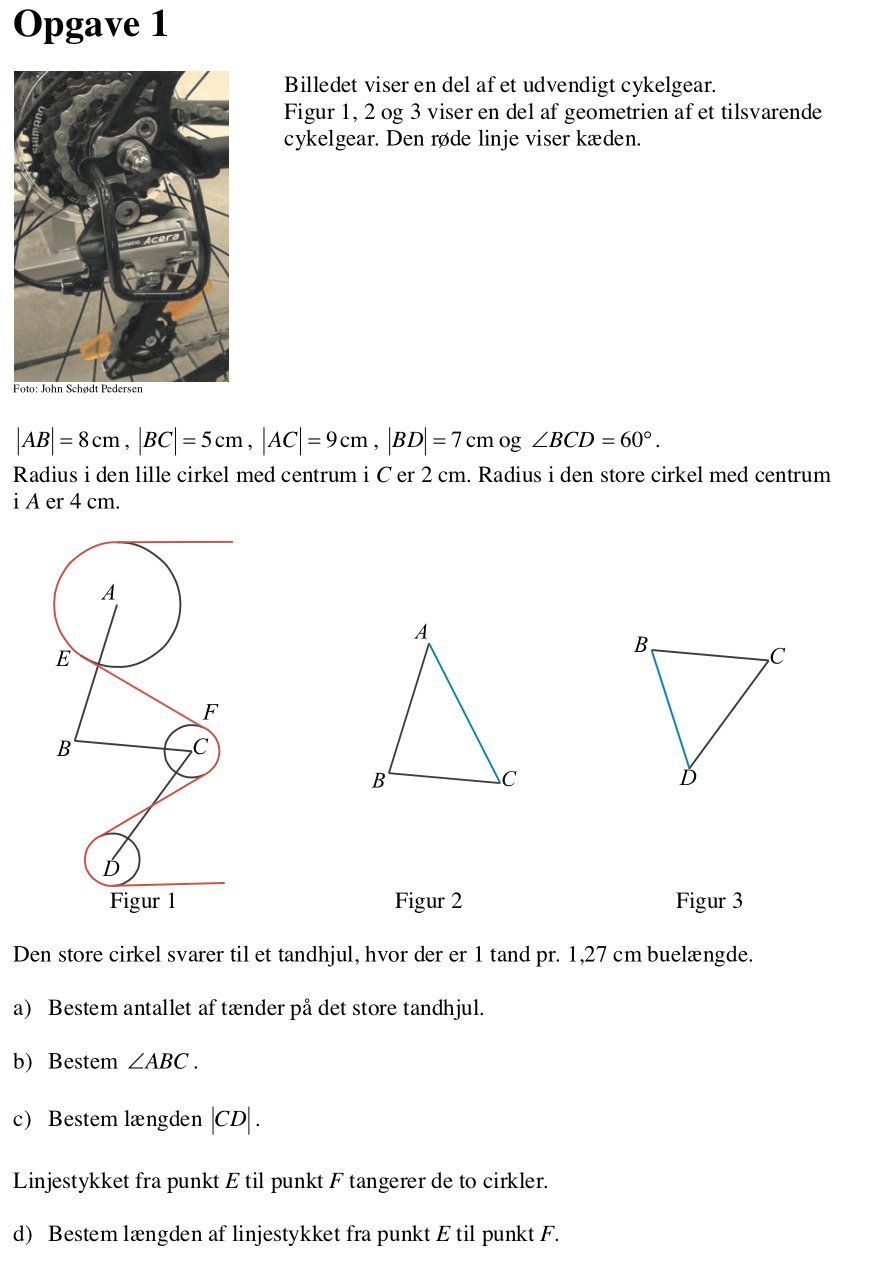
Svar på opgave 1:

1. For at finde antallet af tænder på det store tandhjul, skal man først finde omkredsen af det. Omkredsen er 2·π·4 cm = 25,13 cm. Afstanden mellem hvert tandhjul langs kanten er 1,27 cm pr. tand og dermed er antallet af tænder: 25,13 cm/(1,27 cm/tand) = 19,8 tænder = 20 tænder

2. Man bruger en cosinusrealtion og får i Ti-Nspire:

   solve(cos(x*1.°)=(8²+5²-9²)/(2*8*5),x)|0<x<180 ▸ x=84.2608

   Dvs. ∠ABC er 84,3°

3. Man bruger en cosinusrealtion og får i Ti-Nspire:

   solve(cos(60*1.°)=(x²+5²-7²)/(2*x*5),x) ▸ x=−3. or x=8.

   Dvs. |CD| = 8 cm

4. For at finde |EF| forbinder man A med E, C med F og A med C. Dermed får man to ensvinklede og retvinklede trekanter, der mødes i et punkt P.

   

   De er retvinkelde fordi EF ligger på en fælles tangent, der står vinkelret på radius i begge cirkler. De er ensvinklede fordi de begge har en ret vinkel, ∠APE = ∠CPF og fordi den sidste vinkel er lig med 180° minus summen af de andre vinkler, som er ens for begge trekanter.

   Man kender de to radier |AE| = 4 og |CF| = 2. Ud fra dem finder man skaleringsfaktoren mellem de to trekanter APE og CPF. Den bliver 4/2 = 2. Man ved desuden, at |AC| = 9 cm. Dermed er |AP| = 6 cm og |PC| = 3 cm. Disse sider er hypotenuse i hver sin trekant.

   Derpå får man ved hjælp af Pythagoras læresætning at: |EP| = √[|AP|² - |AE|²] = √[6² - 4²] = √20 = 2·√5. Til dette skal lægges |PF| som ved hjælp af skaleringsfaktoren fås til: √5.

   Til sammen får man at |EF| er (2·√5 + √5) cm = 3·√5 cm = 6,71 cm

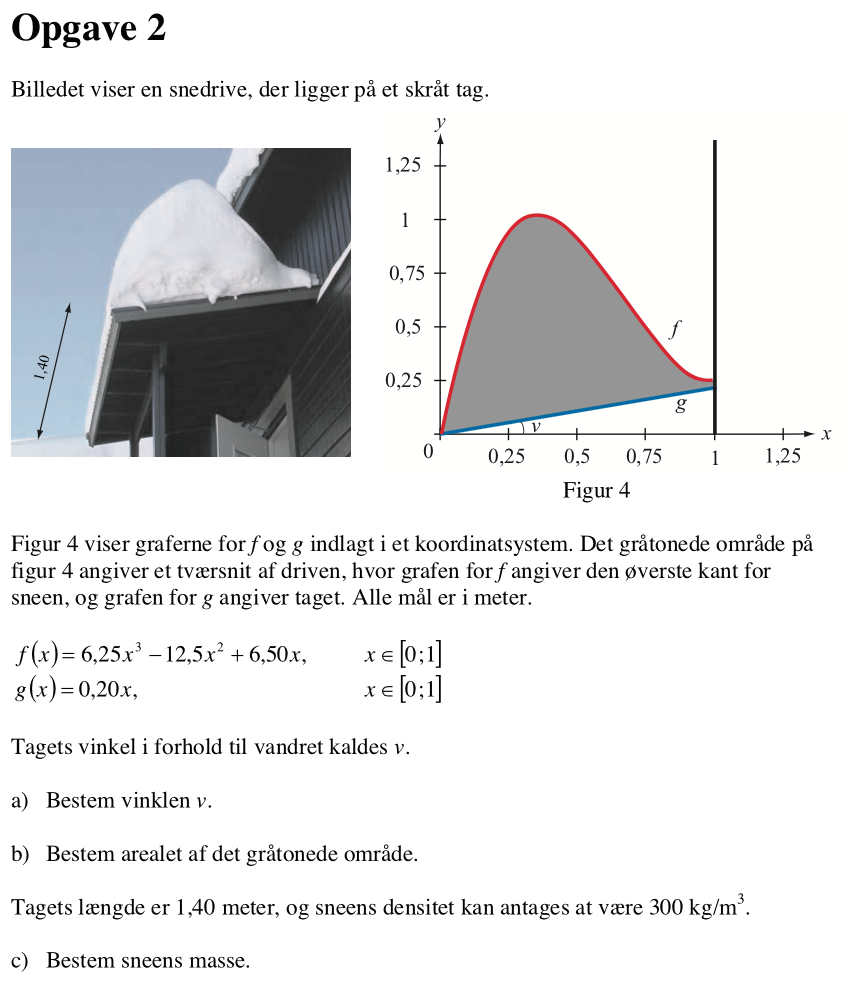
Svar på opgave 2:

1. Vinklen v indgår i en retvinklet trekant. Der gælder, at tan(v) = g(1)/1 = 0,2. Denne ligning løses i Ti-Nspire med hensyn til v:

   solve(tan(v*1.°)=0.2,v)|0<v<90 ▸ v=11.3099

   Vinklen v = 11,3°

2. Arealet af det grå område er integralet fra x = 0 til x = 1 af f(x) - g(x). Dette beregnes i Ti-Nspire:

   f(x):=6.25*x³-12.5*x²+6.5*x ▸ Udført

   g(x):=0.2*x ▸ Udført

   Integral(f(x)-g(x),x,0,1) ▸ 0.54583

   Dvs. arealet er 0,546 m²

3. Sneens masse findes som rumfang gange massefylde af sne:

   Sneens masse = (0,5458 m²)·(1,4 m)·(300 kg/m³) = 229,25 kg

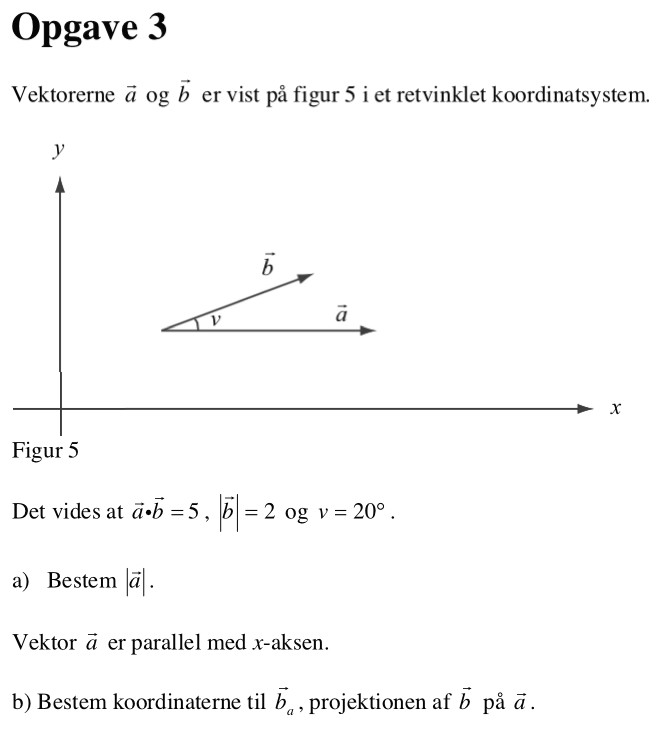
Svar på opgave 3:

1. Man kalder længden af vektor a for x og bruger formlen for vinklen mellem to vektorer og får i Ti-Nspire:

   solve(cos(20*1.°)=5/(x*2),x) ▸ x=2.660

   Dvs. længden af vektor a er 2,66

2. Da a er parallel med x-aksen er b_a det også. Derfor er y-koordianten til b_a lig med 0. x-koordinaten er 2·cos(20°) = 1,87939.

   Dvs. koordinaterne til b_a = (1,879;0)

Svar på opgave 4:

1. Tegnet i Ti-Nspire:

   

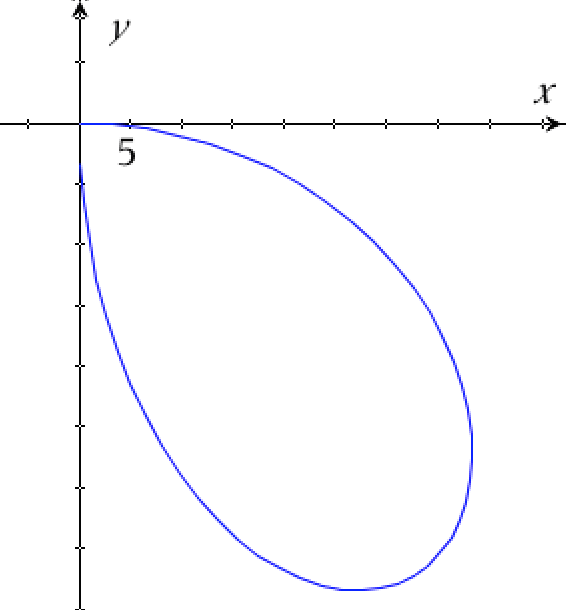
2. Hastighedsvektoren v(t) er stedvektoren differentieret, dvs v(t) = r'(t). Man opretter r(t) i Ti-Nspire:

   r(t):=[50*sin(1.*k*t)*cos((1./2)*k*t),−50*sin(1.*k*t)*sin((1./2)*k*t)] ▸ Udført

   Man oretter hastighedsvektoren for k = 0,5:

   v(t):=derivative(r(t),t) ▸ Udført

   Man finder hastighedsvektoren for t = 2 og k = 0,5:

   v(2)|k=0.5 ▸ [6.81121,−15.7066]

   Dvs. hastighedsvektoren for t = 2 sekunder og k = 0,5 er (6,81;−15,7)

3. For at vise at punktet altid er det samme, indsætter man t = 1/(2k) i formlen for r(t) og får i Ti-Nspire:

   r(1/(2*k)) ▸ [23.226,−5.9306]

   Da det ses, at k ikke indgår i koordinaterne for punktet, er det altid det samme, når t = 1/(2k).

4. Man skal finde den k-værdi, der giver en hastighedsvektoren en længde på 50, når t = 2. I Ti-Nspire beregner man længden af v(t) ved hjælp af kommandoen norm() og får:

   solve(norm(v(1/(2*k)))=50,k)|k<0 ▸ k=1.0992

   Dvs. k må maksimalt blive 1,099

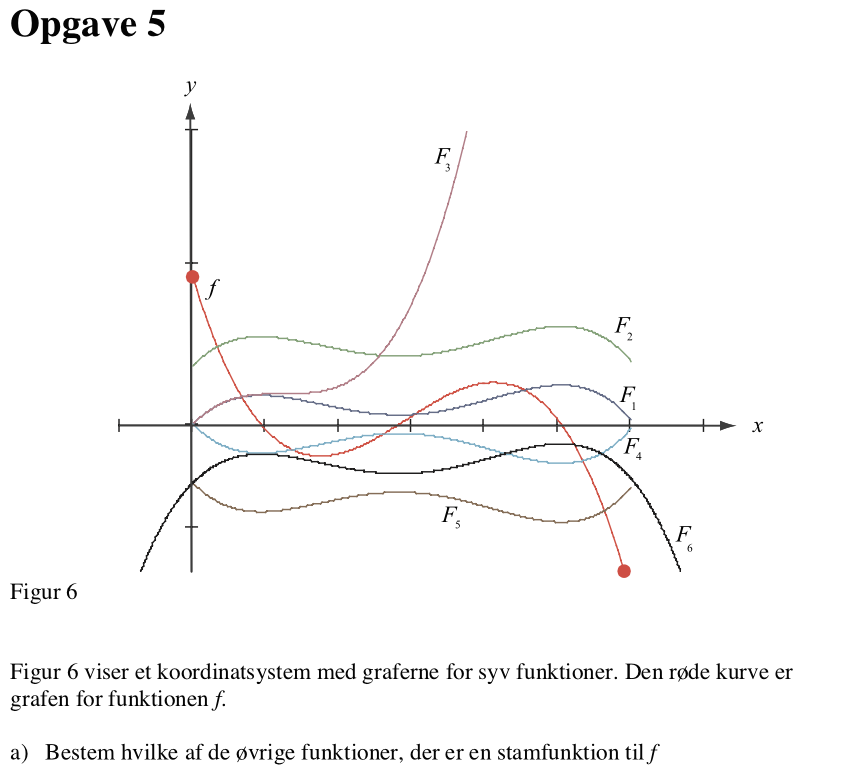
Svar på opgave 5:

1. Funktionen f viser hældningen for kurven. FUnktionen skal vokse fra 0 til det første punkt, hvor f skærer x-aksen. Her skal funkrionen have lokalt maksimum. Derefter skal funktionen aftage indtil det næste punkt, hvor f skærer x-aksen. Her har funktionen minimum. Derfter vokser funktionen igen og antager nyt lokalt maksimum det sidste sted, hvor f skærer x-aksen.

   Dette passer med F₁ og F₂.

   (Det passer ikke med F₆, der har samme facon, men et andet definitionsinterval end f.)

Svar på opgave 6:

1. Kurven med tendenslinje tegnet i TI-Nspire:

   

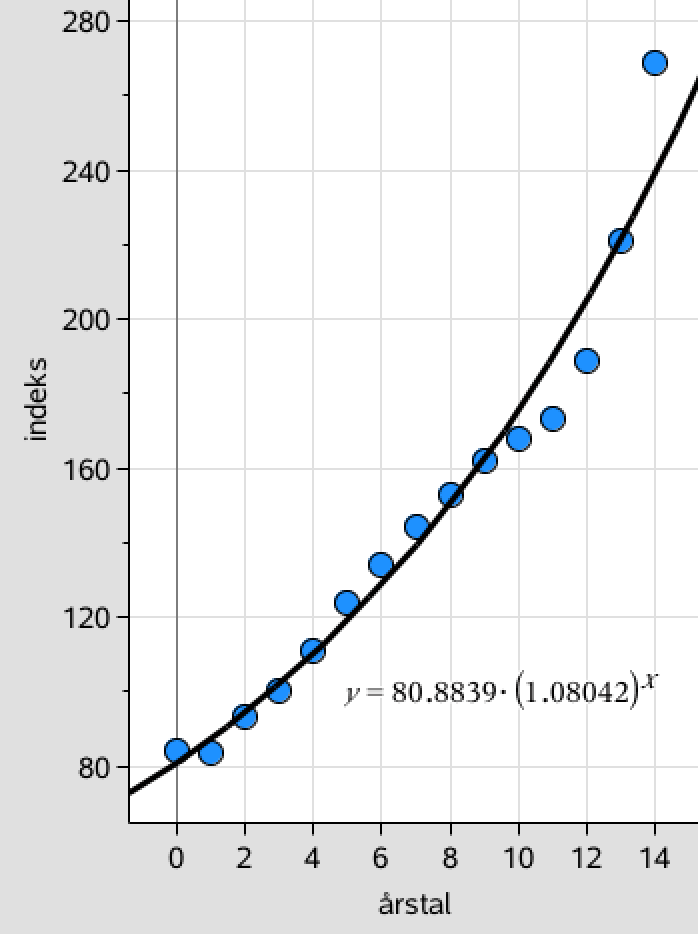
2. Af tendenslinjen i a) fremgår det, at a = 1,0804 og b = 80,88

3. Man skal finde f(2007-1992) = f(15) og sammenligne det med 282. Man får at f(15) = 80,88·1,0804¹⁵ = 258. Dette ses at være mindre end det faktiske resultat.

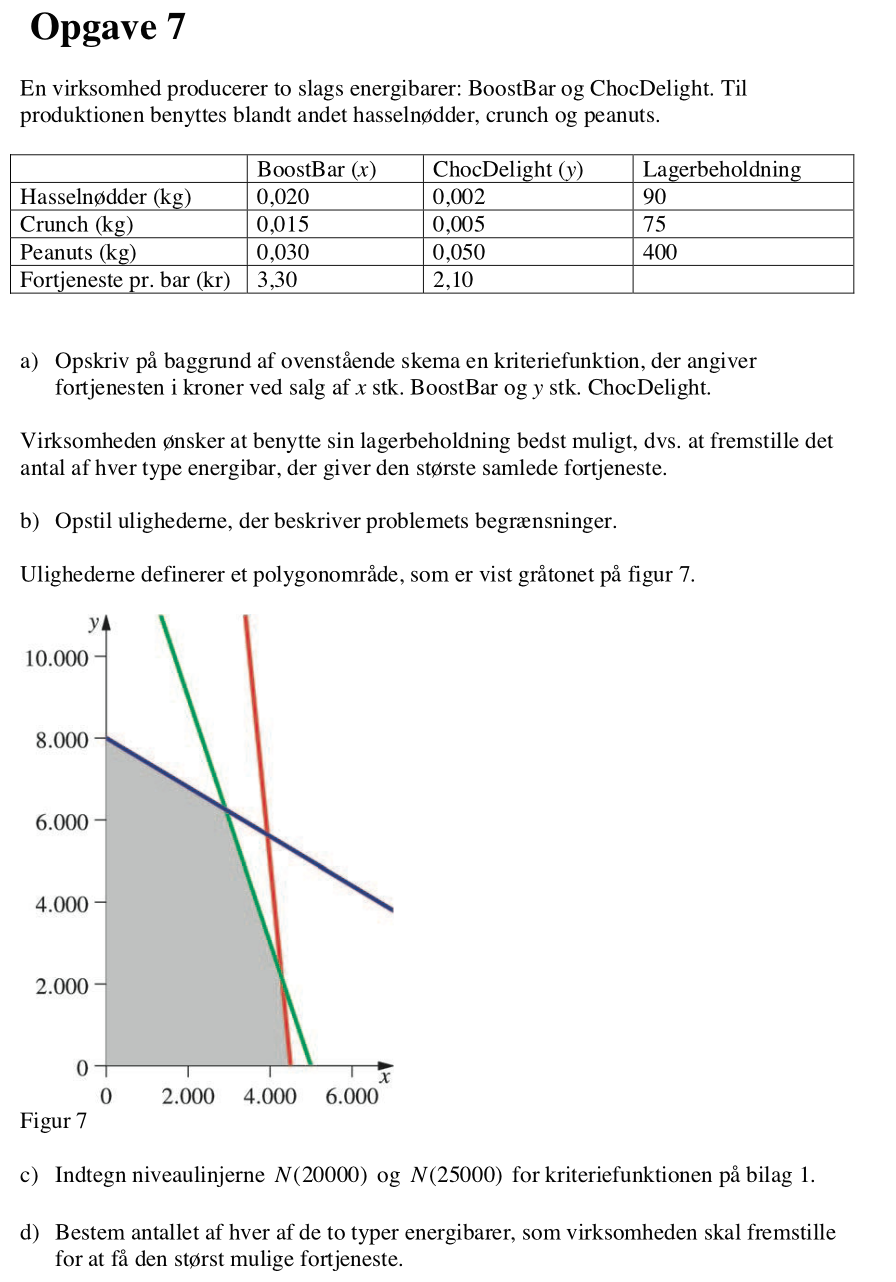
Svar på opgave 7:

1. Kriteriefunktionen aflæses af nederste række i tabellen til: f(x,y) = 3,30x + 2,10y

   Her er x antallet af BoostBarer og y er antallet af ChocDeligth barer, der produceres.

2. Ulighederne aflæses af de tre øverste rækker i tabellen til:

   0,020x + 0,002y ≤ 90

   0,015x + 0,005y ≤ 75

   0,030x + 0,050y ≤ 400

3. Nedenunder er de to niuveau-linjer tegnet i Geogebra.

   

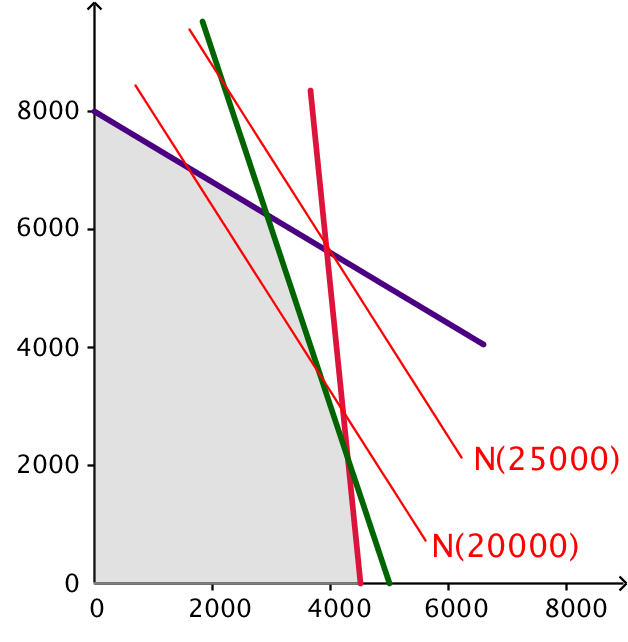
   De er beregnet ved at sige: N(20000): f(x,y) = 2,10x + 3,30y = 20.000 ⇒ y = 1,57x + 9524

   N(25000): f(x,y) = 2,10x + 3,30y = 25.000 ⇒ y = 1,57x + 11905

4. For at finde optimumspunktet parallelforskyder man niveuakurverne fra opgave c) til man finder den kurve der går gennem netop et punkt på polygonen, når man bevæger sig væk fra (0,0). Dette punkt er skæringen mellem den lilla og den grønne linje der er (x,y) = (2917,6250).

   

   Dvs. maksimum fortjeneste fås for en produktion på 2917 BoostBarer og 6250 ChocDeligter.