Svar på opgave 1:
-
Man skal vise at de to stykvise funktioner har sammen værdi i x = 22. Man får i TI-Nspire:
0.046875*(x-14)2+5.1|x=22 ▸ 8.1
7.3+sqrt(1-(x-22.6)2)|x=22 ▸ 8.1
Da man får samme værdi for de to delfunktioner, er xA = 22.
(Det er dog ikke noget fuldstændigt bevis)
-
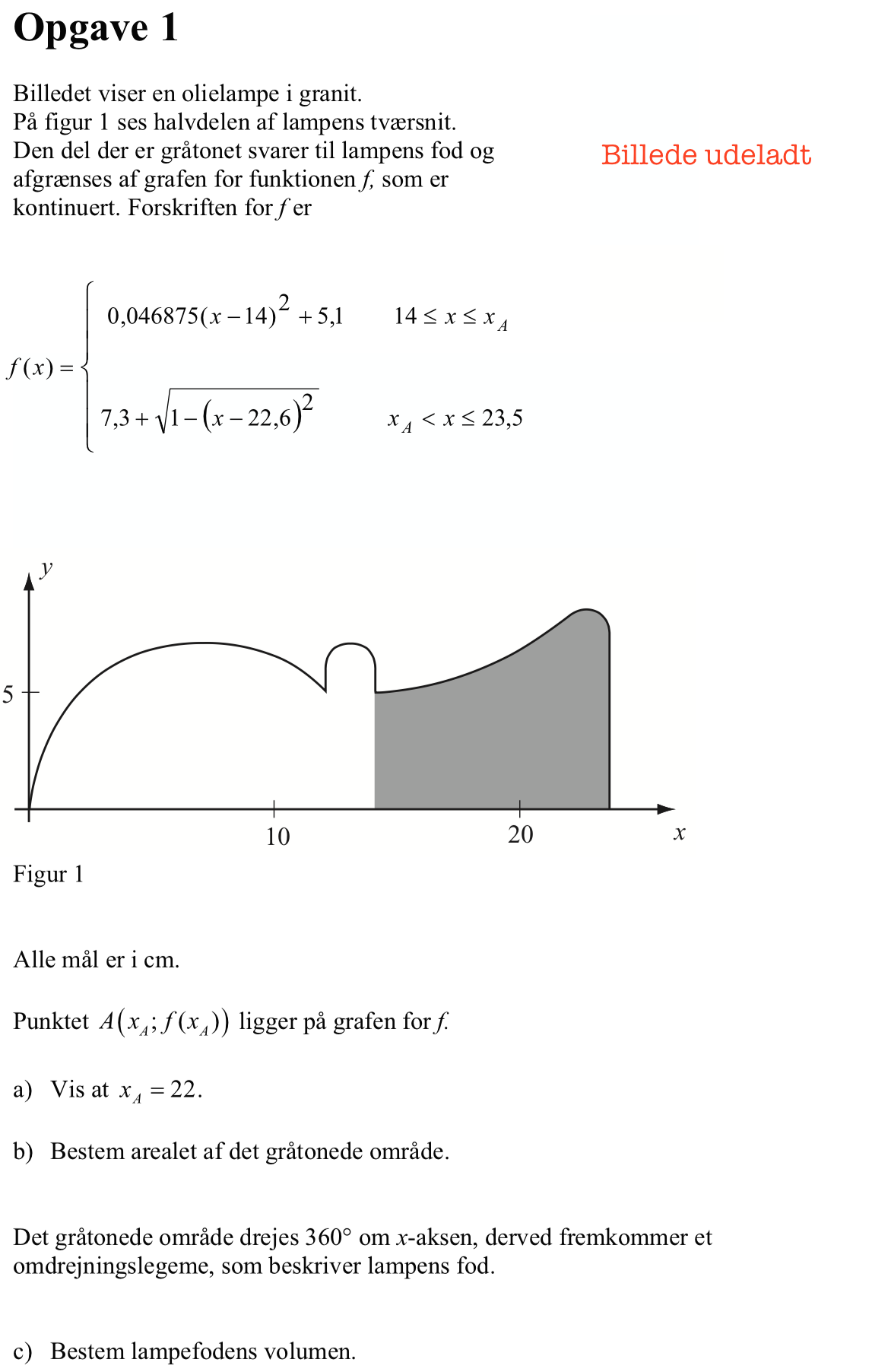
Arealet er integralet af den første delfunktion fra x = 14 til x = 22 plus integralet af den anden delfunktion for x = 22 til x = 23,5. Det giver i Ti-Nspire:
Integral(0.046875*(x-14)2+5.1,x,14,22)+Integral(7.3+sqrt(1-(x-22.6)2),x,22,23.5) ▸ 61.0678
Dvs. arealet af det grå område er 61,07
-
Man skal bruge formlen for rumfanget af et legeme, der fremkommer ved drejning af en kurve 360° om x-aksen. Den skal bruges på begge de to delfunktioner:
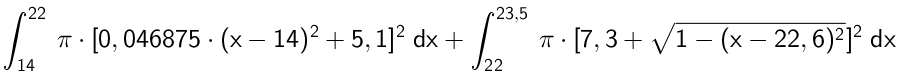
Man får i Ti-Nspire:
Integral(π*(0.046875*(x-14)2+5.1)2,x,14,22)+Integral(π*(7.3+sqrt(1-(x-22.6)2))2,x,22,23.5) ▸ 1270.5847
Dvs. lampefodens rumfang er 1270,6 cm3 = 1,27 L
Svar på opgave 2:
-
Arealet af hullet er π·(2,5 cm)2 = 19,63 cm2
-
Arealet af en regulær femkant med sidelængden 7 er (5/4)·tan(54°)·(7 cm)2 = 84,303 cm2
Arealet af pladen er (12 cm)2 = 144 cm2
Den procentdel som femkanten udgør af pladeresten er (84,303/144)·100 % = 58,5 %
-
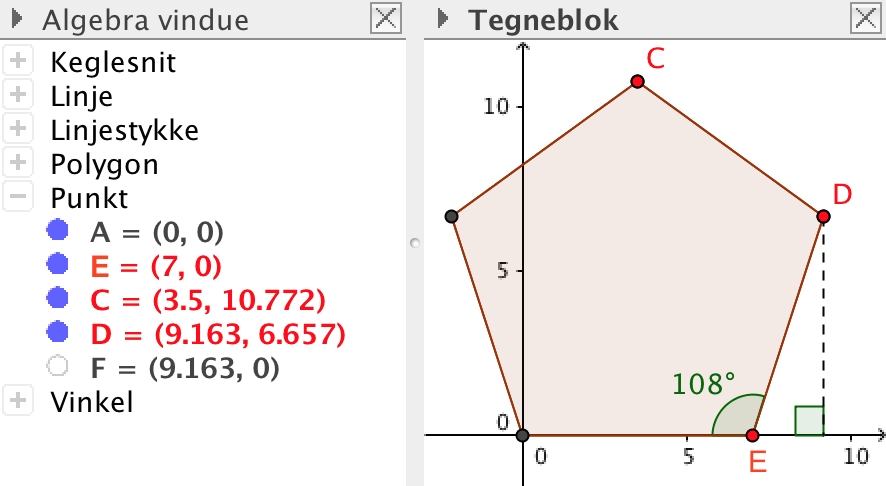
På grund af symmetri har C x-koordinaten 7/2 = 3,5. Punktets y-koordinat er lig med højden af femkanten, som er 1,539·7 = 10,77. Dvs. C = (3,5;10,77)
Punktet D har x-koordinaten: 7 cm + 0,5·(bredde af femkant - 7). Bredden er 1,6180·7 = 11,326. Det giver: D's x-koordinat er 7 + 0,5·(11,326 - 7) = 9,163. D's y-koordinat findes som 7·sin(180°-108°) = 7·sin(72°) = 6,657. Dermed er D = (9,163;6,657)
Punktet E ligger 7 cm fra koordinatsystemets nulpunkt på x-aksen. Dermed er E = (7,0).
Løst i Geogebra:
-
Centrum af cirklen er toppunkt i en trekant med højden (7/2)·tan(54°) = 4,8173. Centrum befinder sig lodret over midten af siden AE. Dvs. O har koordinaterne (3,5;4,8173). Radius af cirklen er 2,5.
Dermed har cirklen ligningen: (x - 3,5)2 + (y - 4,817)2 = 2,52
Svar på opgave 3:
-
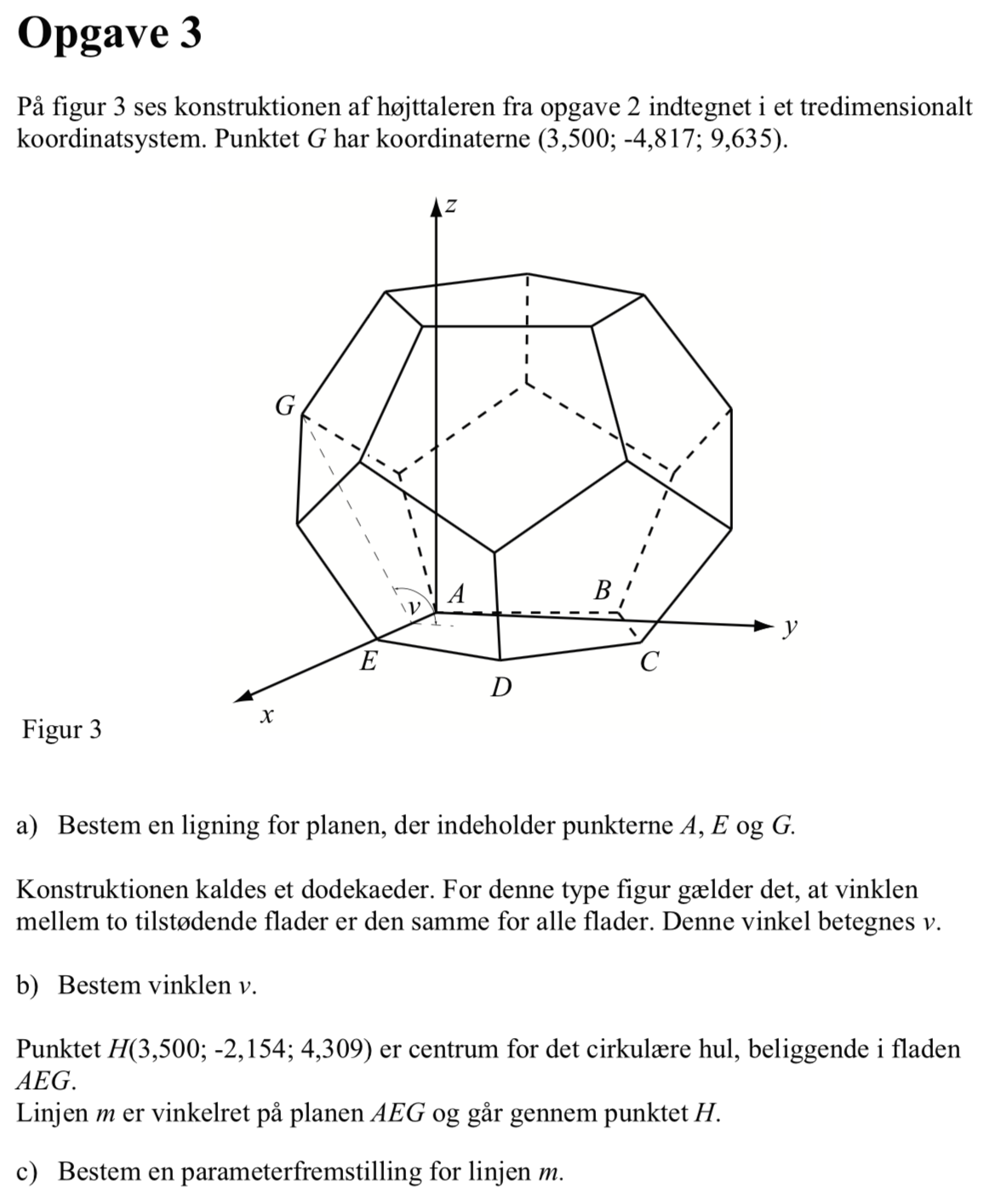
For at bestemme planens ligning finder man først en normavektor til den. Denne findes ved hjælp af krydsproduktet af de to vektorer AG og AE, der begge ligger i planen. Krydsproduktet findes i Ti-Nspire til:
crossP([7,0,0],[3.5,−4.817,9.635]) ▸ [0.,−67.445,−33.719]
Denne vektor forkortes med −33.719 og man får følgende normalvektor til planen n = [0,000;2,000;1,000].
Da planen går gennem (0,0,0) bliver det konstante led i ligningen lig med 0. Man får derfor planens ligning til 0,000·x + 2,000·y + 1,000·z + 0 = 0 eller kortere 2,000·y + 1,000·z = 0
-
Man skal finde vinklen mellem planen fra opgave a) og xy-planen. Denne plan har normalvektoren k = (0,0,1). Man finder v ved hjælp af formlen for vinkel mellem n og k:
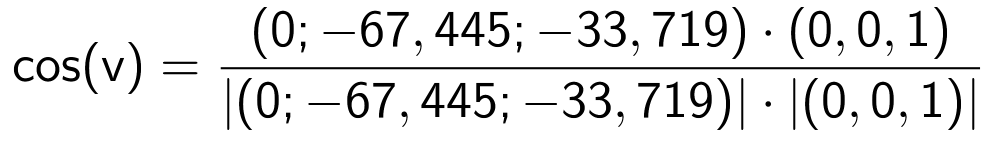
Dette løses i Ti-Nspire:
solve(cos(x*1.°)=dotP([0.,−67.445,−33.719],[0,0,1])/(norm([0.,−67.445,−33.719])*norm([0,0,1])),x)|0<x<180 ▸ x=116.56
Dvs. v = 116,6°
(Det ses som kontrol af tegningen, at vinklen er stump).
-
Linjen m har vektoren n som retningsvektor. Da linjen går gennem punktet (3,500;-2,154;4,309) kan dens parameterfremstilling skrives:
m: (x,y,z) = (3,500;-2,154;4,309) + t·(0;2,000;1,000), t∈R
Svar på opgave 4:
-
Ligningerne for linjerne er:
y = 4 - 4x
y = 3 - (4/3)x
y = 1 - (1/5)x
-
Man omskriver f(x,y) = 3x + y til y = -3x + f(x,y).
Ved en grafisk betragtning ses, at denne linje ligger inden for polygonen og antager sin mindste værdi, når den går gennem det punkt, hvor begrænsningslinjerne y = 4 - 4x og y = 1 - (1/5)x skærer hinanden. Dette punkt er P og findes i Geogebra som vist på tegningen:
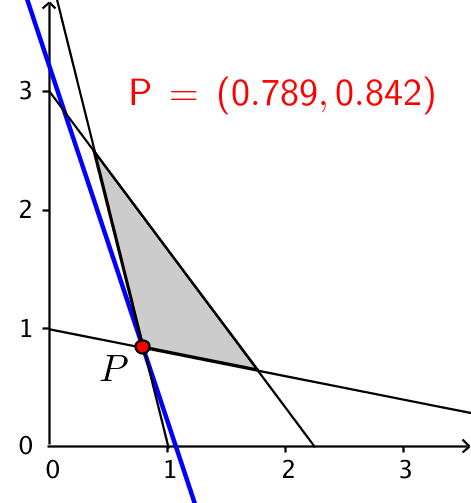
Dvs. P = (0,789;0,842), og mindsteværdien af f(x,y) = 3·0,789 + 0,842 = 3,209.
-
Værdien af a kan højst være 4, da linjen eller bliver for stejl til kun at skære polygoniet i p.
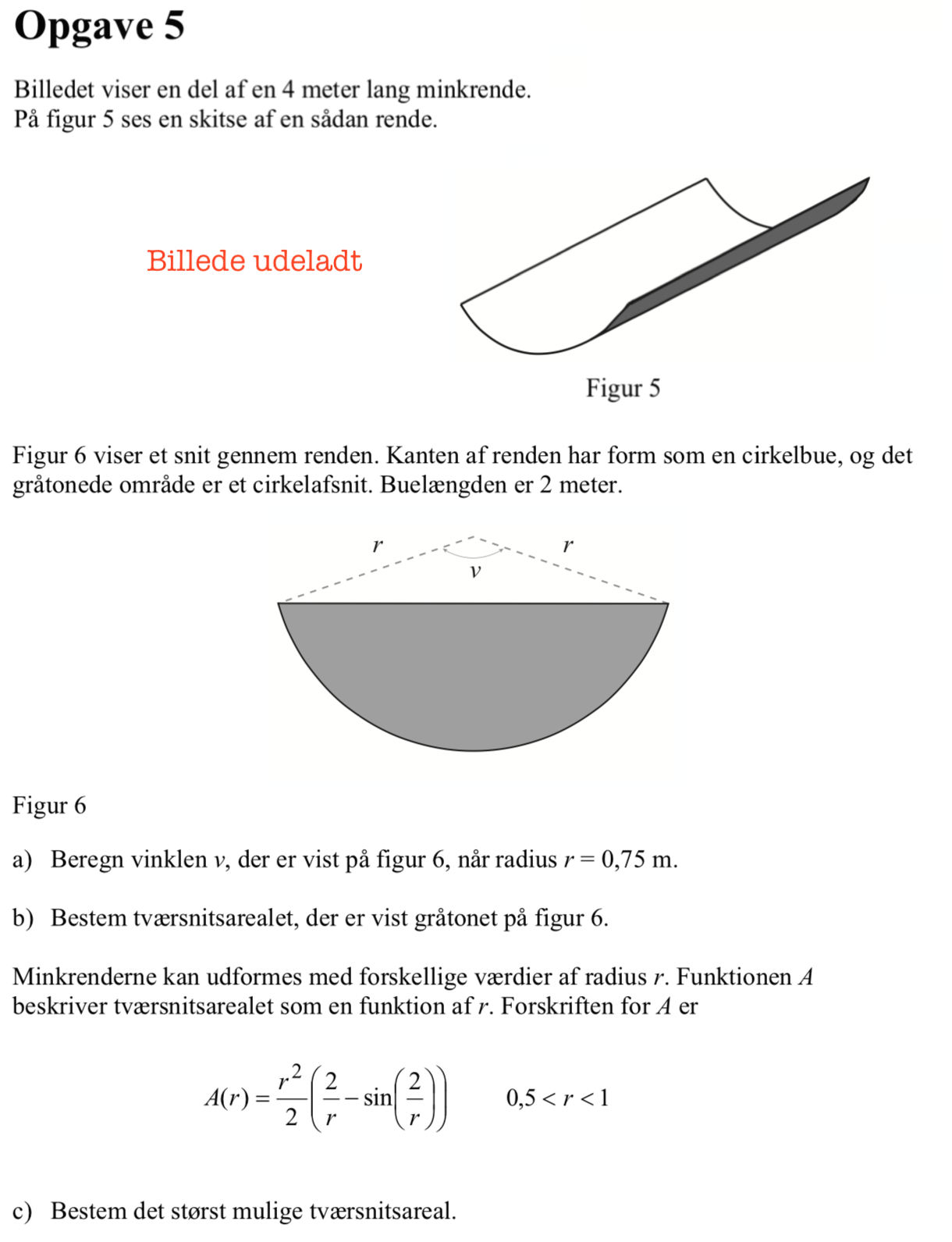
Svar på opgave 5:
-
Sammenhængen mellem buelængden, radius og vinklen i radianer er: v = buelængde/radius = 2/0,75 = 2,6667. Dette omregnes til grader:
2,6667 radianer = 2,6667·(180°/π) = 152,8°
-
Man bruger den angivne formel A(r), der gælder, når buelængden er 2 m, og får arealet
(0,752/2)·(2/0,75-sin(2/0,75)) m2 = 0,621 m2
-
Man opretter A(r) i Ti-Nspire:
a(r):=(r2/2)*(2/r-sin(2/r)) ▸ Udført
Man beregner den radius, der giver det maksimale areal ved hjælp af fMax-kommandoen i Ti-Nspire:
fMax(a(r),r)|0.5<r<1 ▸ r=0.6366
Denne radius indsættes i A(r) for at finde det maksimale areal, når buelængden holdes konstant 2 m og radius ligger mellem 0,5 m og 1 m:
a(0.63662) ▸ 0.6366
Dvs. det maksimale areal er 0,64 m2

Svar på opgave 6:
-
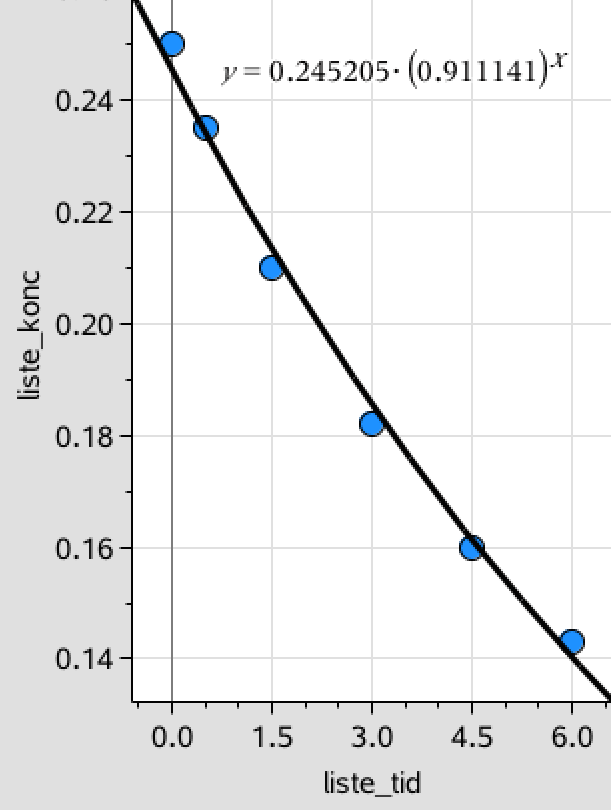
I Ti-Nspire oprettes en liste over målte tider (liste_tid) og en liste over målte koncentrationer (liste_konc).
liste_tid:={0.,0.5,1.5,3.,4.5,6.} ▸ {0.,0.5,1.5,3.,4.5,6.}
liste_konc:={0.25,0.235,0.21,0.182,0.16,0.143} ▸ {0.25,0.235,0.21,0.182,0.16,0.143}
Ud fra disse laves et plot af koncentrationen som funktion af tiden. Dette er gjort nedenunder i Ti-Nspire, hvor der desuden er indtegnet en eksponentiel tendenslinje:
-
Af tendenslinjen y = 0,245·0,911x fundet i Ti-Nspire læser man, at
a = 0,911 og b = 0,245 mol/liter
Svar på opgave 7:
-
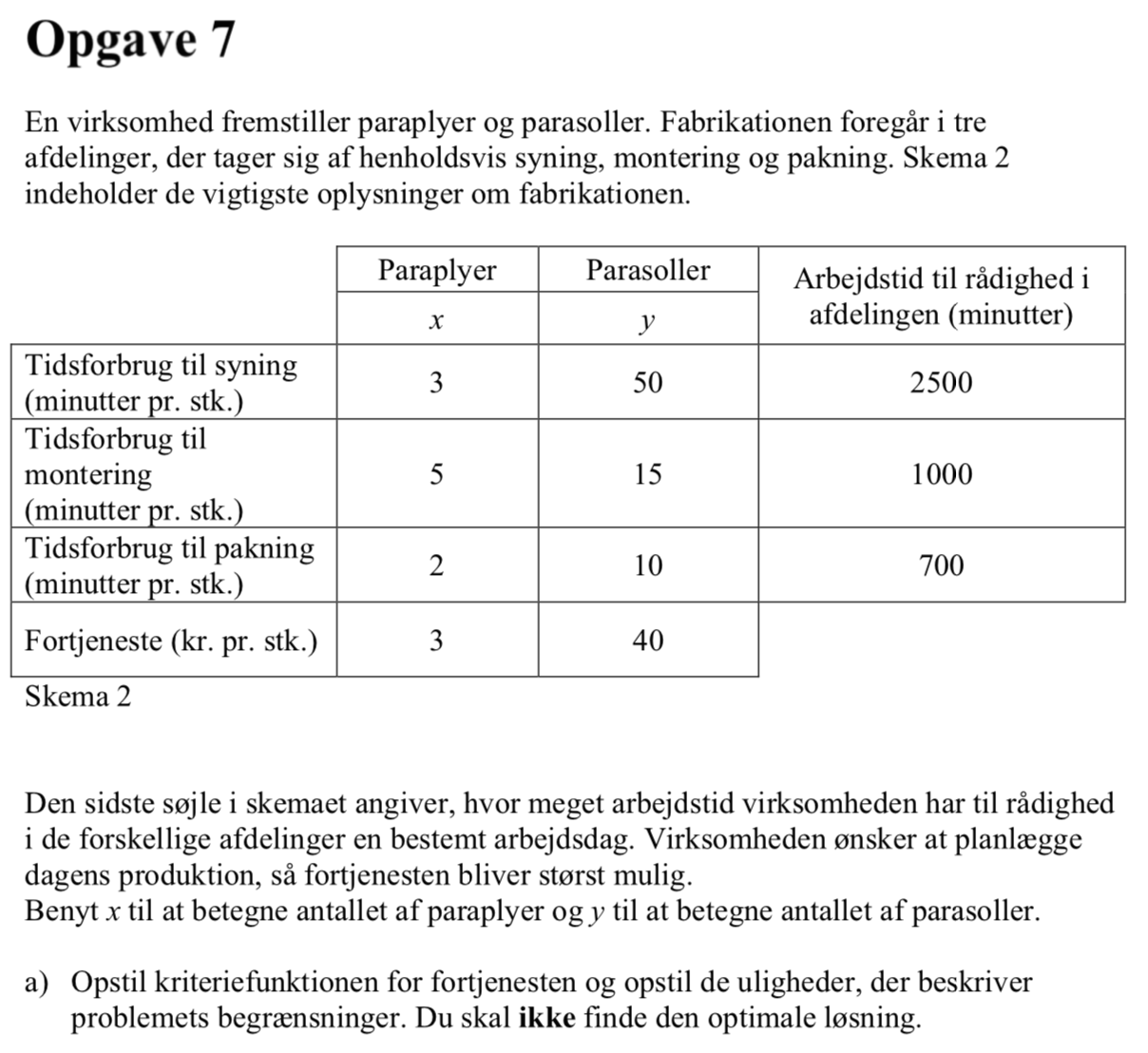
Kriteriefunktionen for fortjenesten findes af nederste linje i tabellen. Den er: f(x,y) = 3x + 40y,
hvor f(x,y) er fortjenesten i kr., x er antal solgte paraplyer og y er antal solgte parasoller.
De tidsmæssige begrænsninger udledes af de tre første vandrette rækker i tabellen (tidsenhed er minutter):
3x + 50y ≤ 2500 (tidsmæssig begrænsning for syning)
5x + 15y ≤ 1000 (tidsmæssig begrænsning for montering)
2x + 10y ≤ 700 (tidsmæssig begrænsning for pakning)