

Svar på opgave 1:
-
Nedenstående graf er lavet i Excel ved hjælp af fire punkter og diagramfunktionen: XY plot med udjævnet kurve.
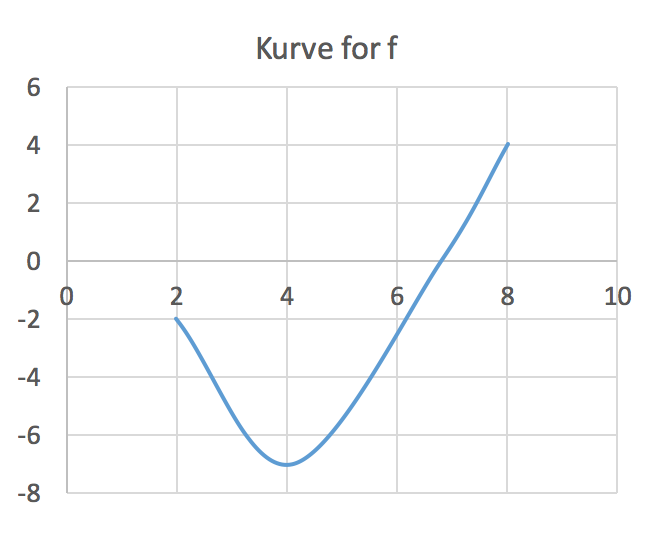
(Se også Graf til opgave 1)
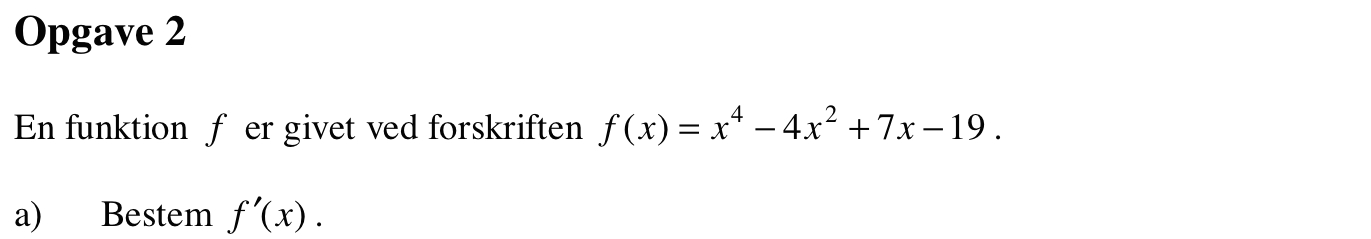
Svar på opgave 2:
-
f´(x) = 4x3 - 8x + 7
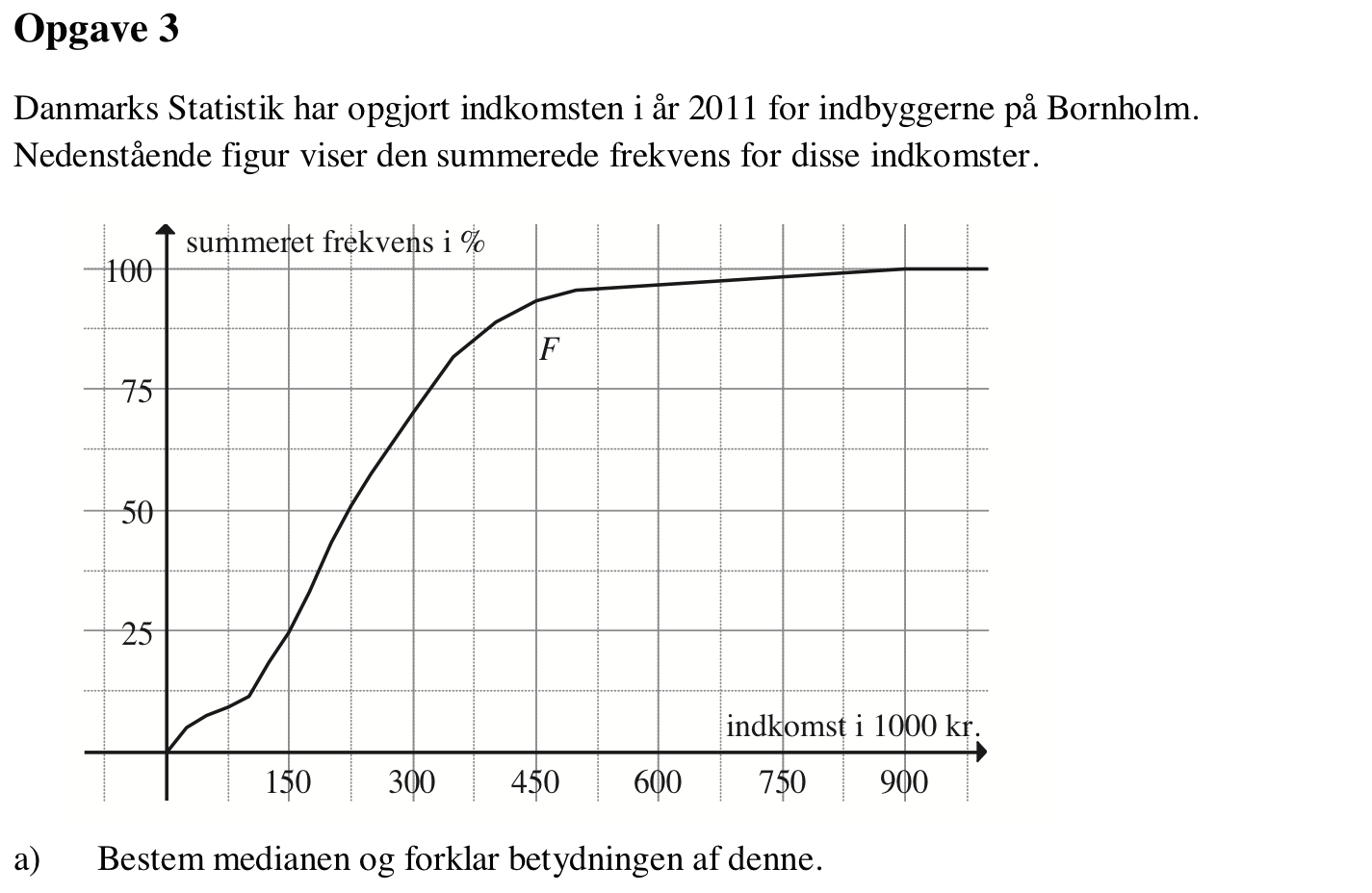
Svar på opgave 3:
-
Af figuren nedenunder aflæses medianen til 220,000 kr. Det er det tal som halvdelen af indkomsterne er mindre end eller lig med.
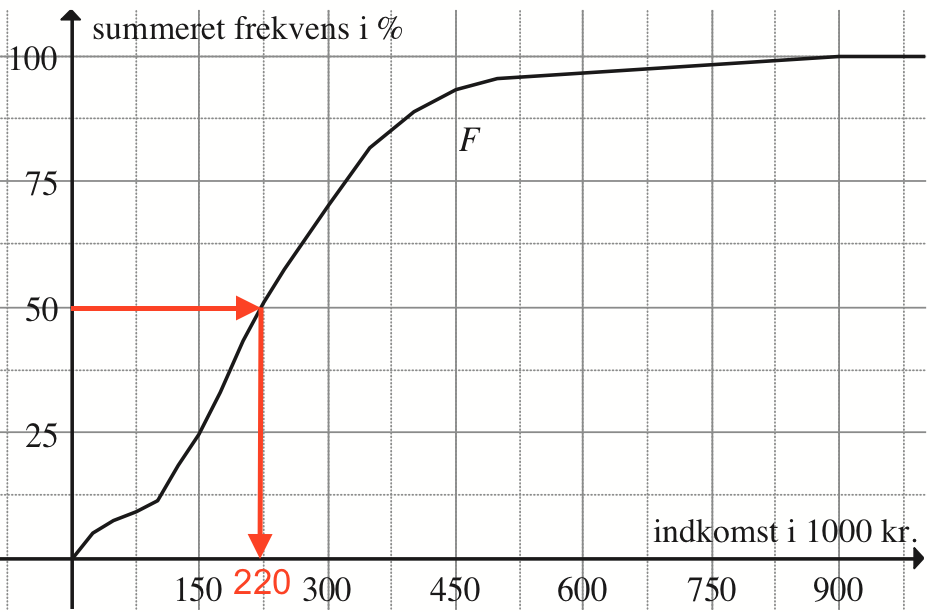
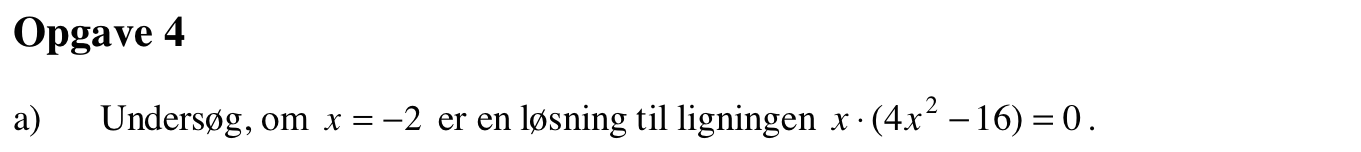
Svar på opgave 4:
-
Man skal gøre prøve og se om x·(4·x2 - 16) er lig med 0, når man indsætter x = -2. Man får:
(-2)·(4·(-2)2 - 16) = (-2)·(4·4 - 16) = (-2)·(16 - 16) = (-2)·0 = 0
Dvs. x = -2 er en løsning til ligningen.

Svar på opgave 5:
-
a er hældningen mellem de to punkter på kurven: a = (25.000 - 30.000)/(150 - 100) = -5.000/50 = - 100. b findes ved at indsætte a og et punkt, her (100,30.000), i ligningen:
30.000 = -100·100 + b ⇒ b = 30.000 + 10.000 ⇒ b = 40.000. Man får:
D(x) = -100·x + 40.000 stk.
Når x = 75 kr./stk. bliver efterspørgslen: D(75) = (-100·75 + 40.000) stk. = 32.500 stk.



Svar på opgave 6:
-
Man skal gøre prøve ved at indsætte x = 2·√a i udtrykket 4·a·x-2 og se om det giver 1. Man får:
4·a·(2·√a)-2 = 4·a·2-2·a-1 = 4·a·(1/4)·(1/a) = 1. Dvs. x = (2·√a) er en løsning til ligningen.
-
2. leddene samles på venstre side af lighedstegnet
3. Udtrykket på venstre side skrives som et produkt af to faktorer (udtrykket faktoriseres)
4. Man bruger nulreglen til at opdele ligningen í to ligninger
5. I anden ligning flytter man det konstante led (-10) over på højre side og tager ln() på begge sider
6. Man finder løsningerne x = 0 og x = 2,30.

Svar på opgave 7:
-
På nedenstående figur, som er lavet i Excel, er udbudspriserne grupperet i 15 intervaller hver med en længde af 250.000 kr. gående fra 0 kr. til 3.500.000 kr. Dernæst er den kumulerede frekvens regnet ud for hver gruppe.
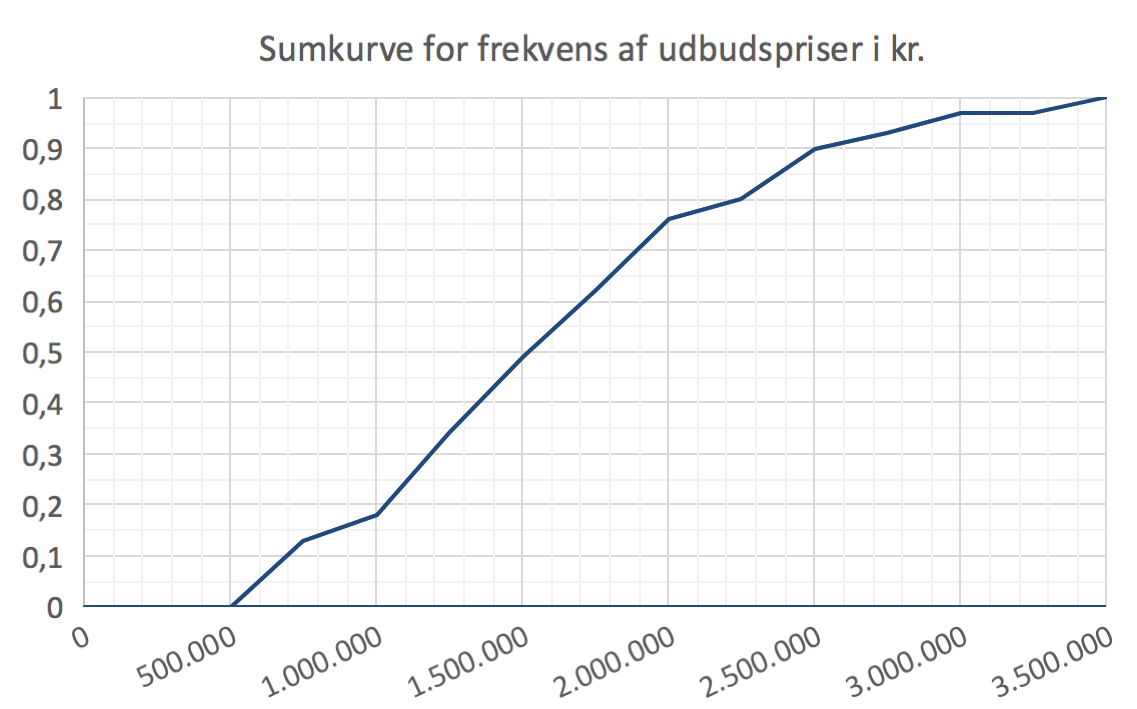
-
Kvartilsættes bregnes i Excel til :
1. kvartil = 1.140.000 kr.,
median = 1.527.500 kr. og
3. kvartil = 1.995.000 kr.
-
Nedenstående figur, som er lavet i Excel, viser sammenhængen mellem størrelse af fritidshuse og deres udbudspris.
Tendenslinjen er U(x) = y = 14.395x + 270.512, hvor x er størrelsen i m2 og U(x) er udbudsprisen i kr.
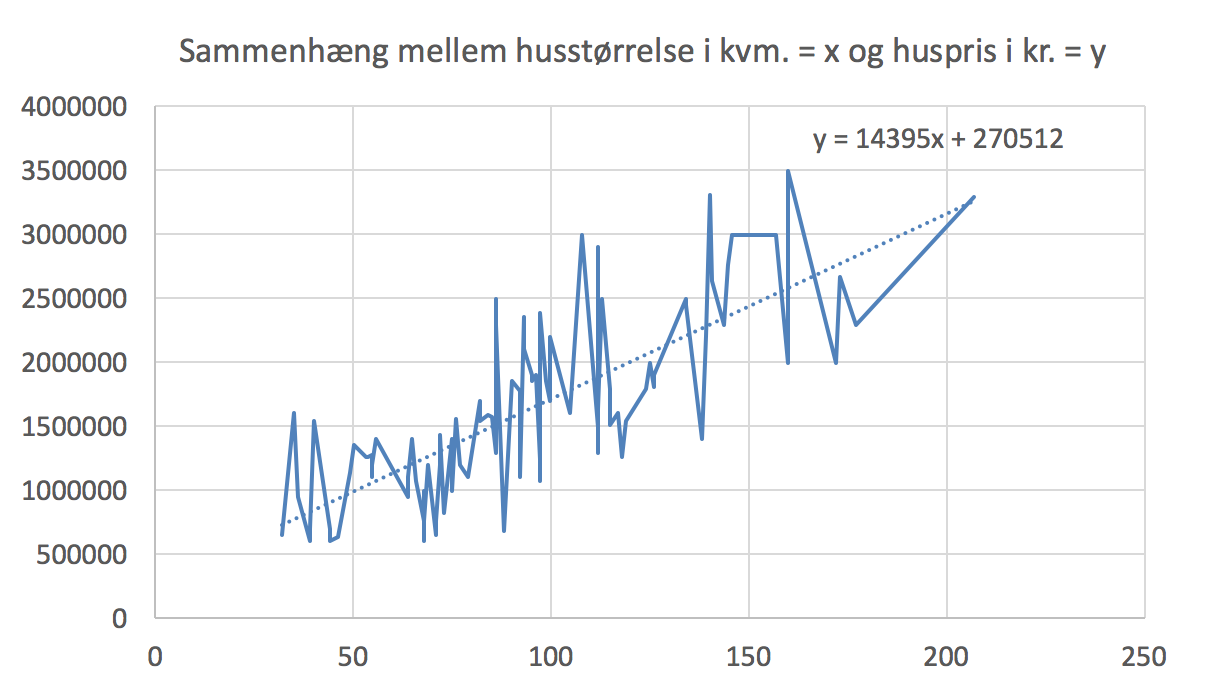
-
Prisen på fritidshuse ligger på omkring 1,5 mio kr. i gennemsnit, og der er en svag sammenhæng mellem fritidshusetsstørrelse og dets udbudspris. Man må regne med, at beliggenheden også spiller en rolle for prisen.
(Se også Fritidshuse)

Svar på opgave 8:
-
Renten er (40.000 kr.)·0,0208 = 832 kr.
Afdraget er ydelse - rente = 1.173 kr. - 832 kr. = 341 kr.
Restgæld: 39.659 kr. + (39.659 kr.)·0,0208 - 1.173 kr. = 39.311 kr.
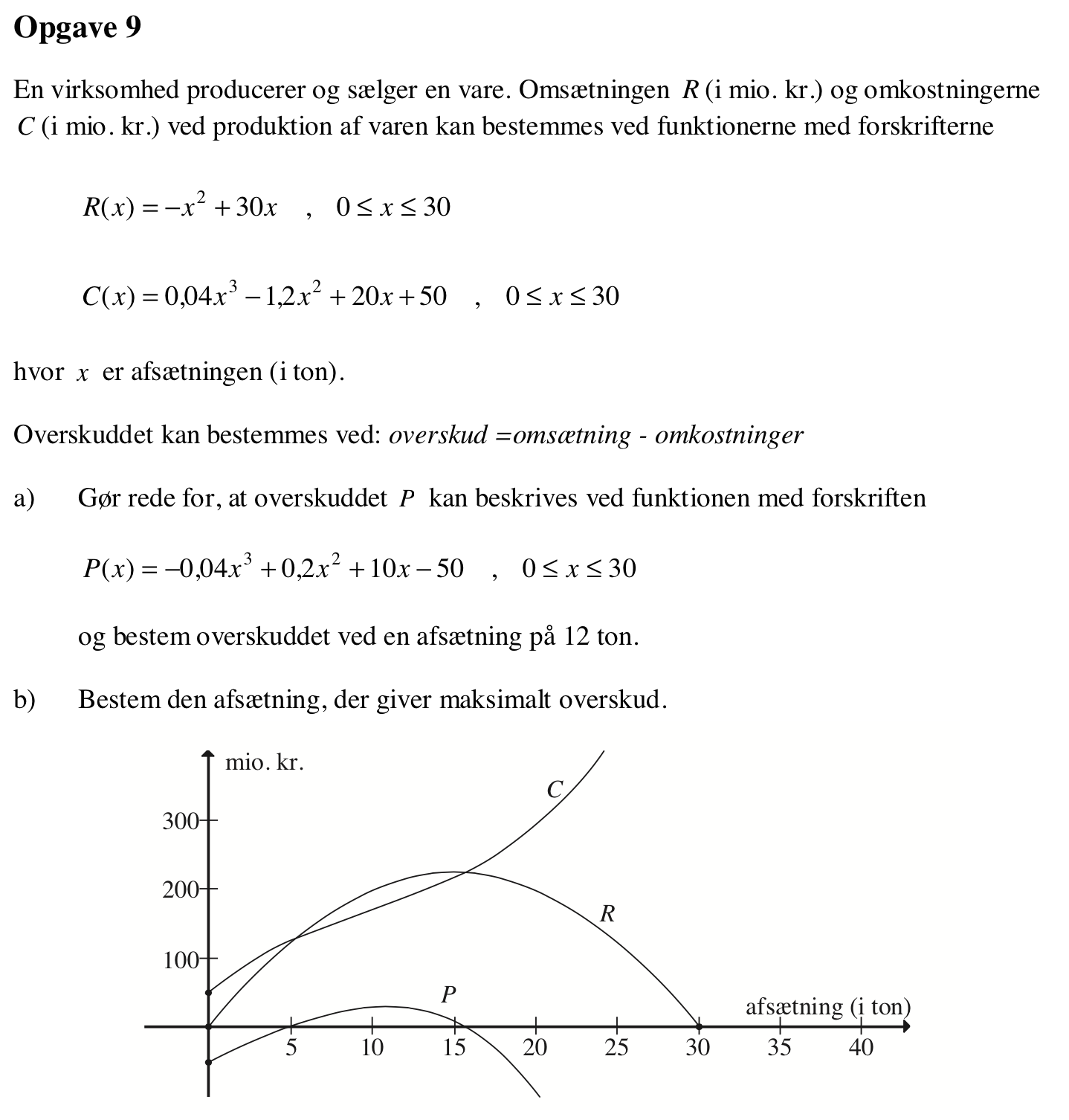
Svar på opgave 9:
-
P(x) = R(x) - C(x) = −x2 + 30x - (0,04x3 - 1,2x2 + 20x + 50) = −0,04x3 + 0,2x2 + 10x - 50
Man skal beregne P(12): Man får i Ti-Nspire:
p(x):=−0.04*x^(3)+0.2*x^(2)+10*x-50 → Udført
p(12) → 29.68
Dvs. overskuddet er 29,7 mio. kr.
-
Man bruger Ti-Nspire kommandoerne:
fMax(p(x),x)|0≤x≤30 → x=10.946
p(10.946) → 30.963
Dvs. maksimumoverskuddet er 30,9 mio. kr.

Svar på opgave 10:
-
Svaret på a) er givet i tabellen Observeret
-
Nulhypotesen er, at svar er uafhængig af landsdel.
Hypotesen forkastes på et 5% signinfikansniveau fordi enten:
1) sandsynligheden for at teststørrelsens værdi kan skyldes tilfældigheder er mndre end 5% eller
2) Den kritiske værdi for en Chi-i anden fordelt stokastisk variabel med to frihedsgrader er mindre end teststørrelsen.
Nedenstående figur viser opgaven løst i Excel.
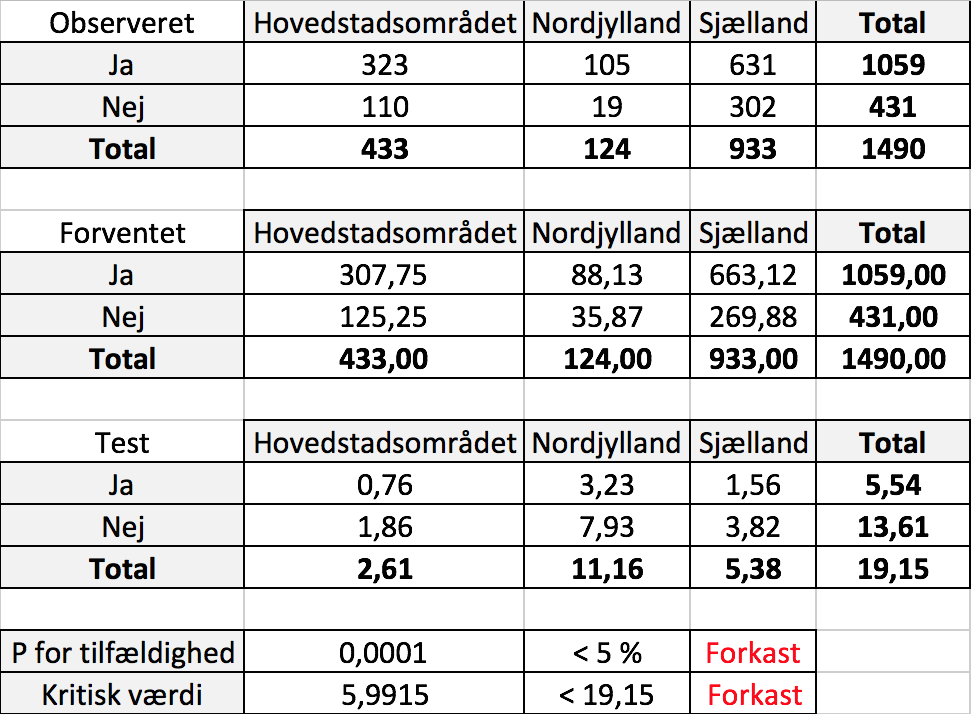
(Se Excel-filen i bunden under Svar-arket for at finde formlerne.)
(Se også Rejsekort)


Svar på opgave 11a:
-
Man bruger Ti-Nspire kommandoen: normCdf(−∞,10,10.75,1) → 0.2266, dvs. sandsynligheden er 0,227.
-
Man bruger Ti-Nspire kommandoen: Beregninger > Statistik > Konfidensintervaller > z-interval for en middelværdi...
Dernæst vælger man Statistik under Data-inputmetode:
og indsætter spredning (beregnet værdi: s, sand værdi: σ), middelværdi (beregnet værdi: x̄, sand værdi: μ), antal observationer (n) og signifikansniveau:
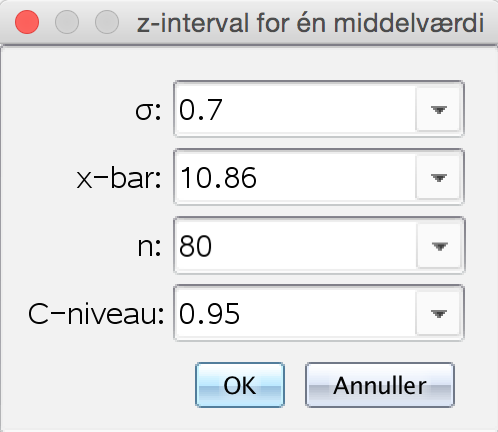
Ved at trykke OK, får man:

Det giver "CLower" = 10.7066 og "CUpper" = 11.0134. Dvs. intervallet er [10,7;11,0].
Svar på opgave 11b:
-
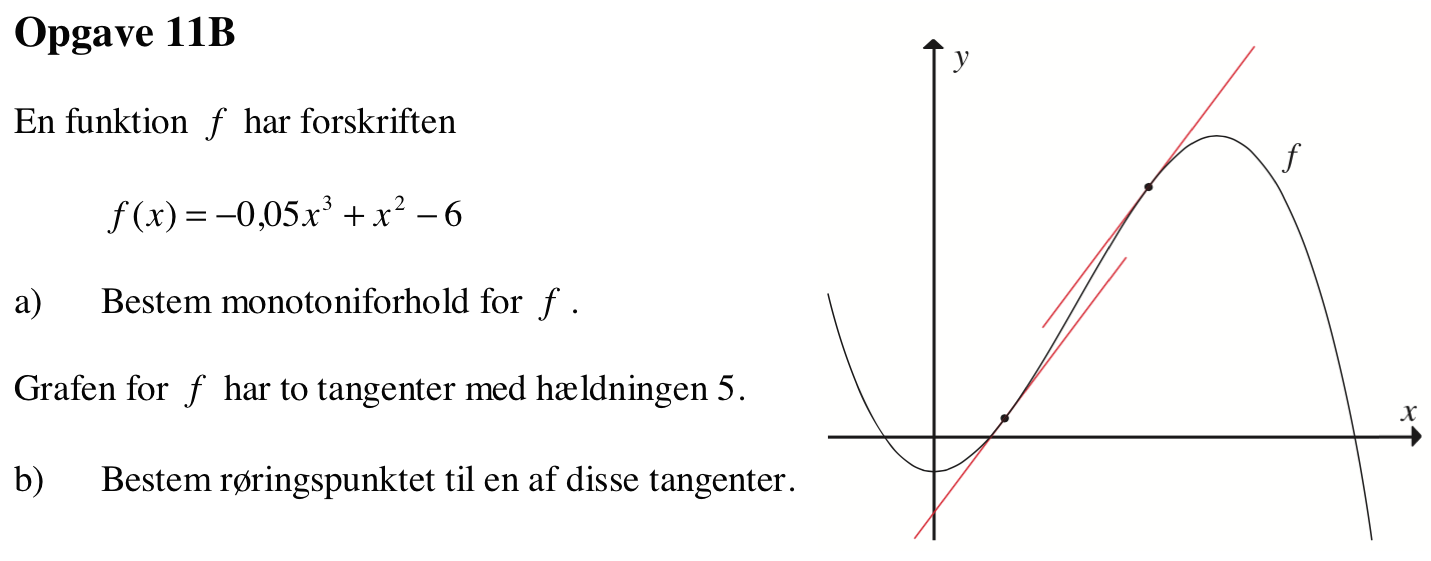
Man bruger kommandoerne:
f(x):=−0.05*x3 + x2 - 6 ▸ Udført
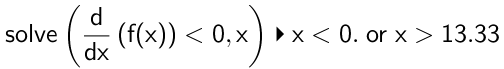
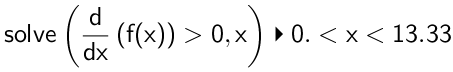
Dvs. monotoniintervallerne er :
f(x) er aftagende for x < 0
f(x) er voksende for 0 < x < 13.33
f(x) er aftagende for x > 13.33
-
Man bruger kommandoen
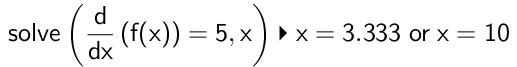
Her vælger man x=3,333 og får maksimumværdien: f(3.333) ▸ 3.259
Dvs. det ene punkt er (3,333;3,259)

Svar på opgave 12b:
-
Forskriften er f(x,y) = 800x + 140y, hvor x er antallet af campinghytter og y er antallet af campingvogne.
-
Ud fra begrænsningerne tegner man polygonområdet som vist på nedenstående tegning lavet i Geogebra.
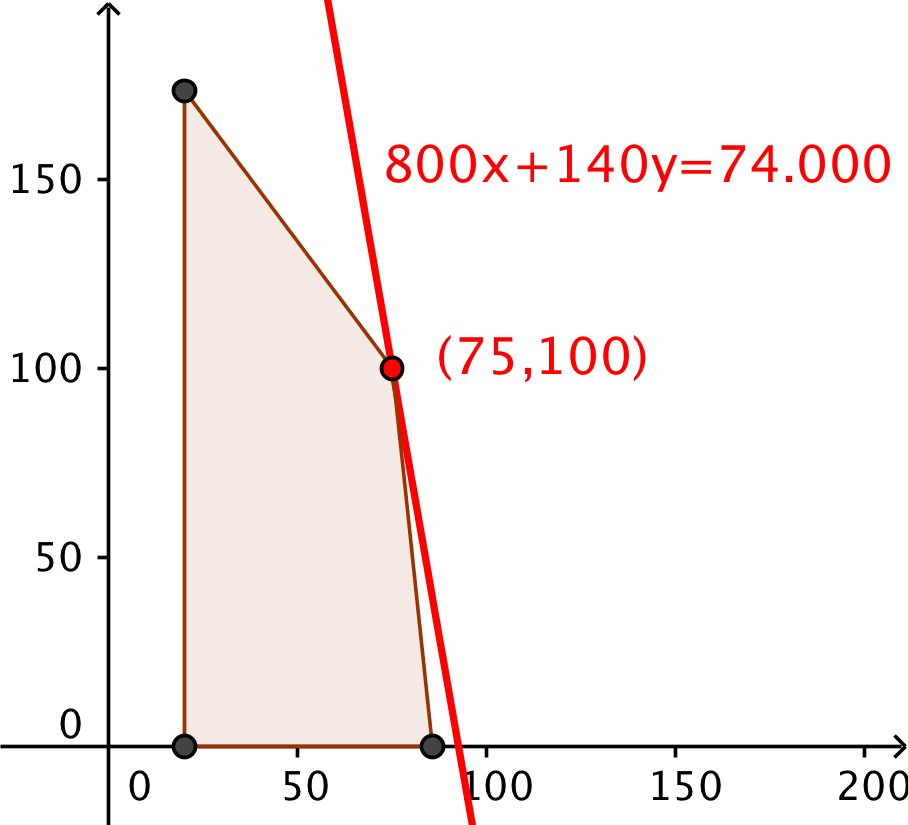
Den niveaukurve, der giver den højeste værdi, er tegnet med rødt.
Maksimum punktet er (75,100), dvs. 75 campinghytter og 100 campingvogne
Maksimumværdien for dækningsbidraget er f(x.y) = 74.000 kr.
Løsning med Excel Problemløser:
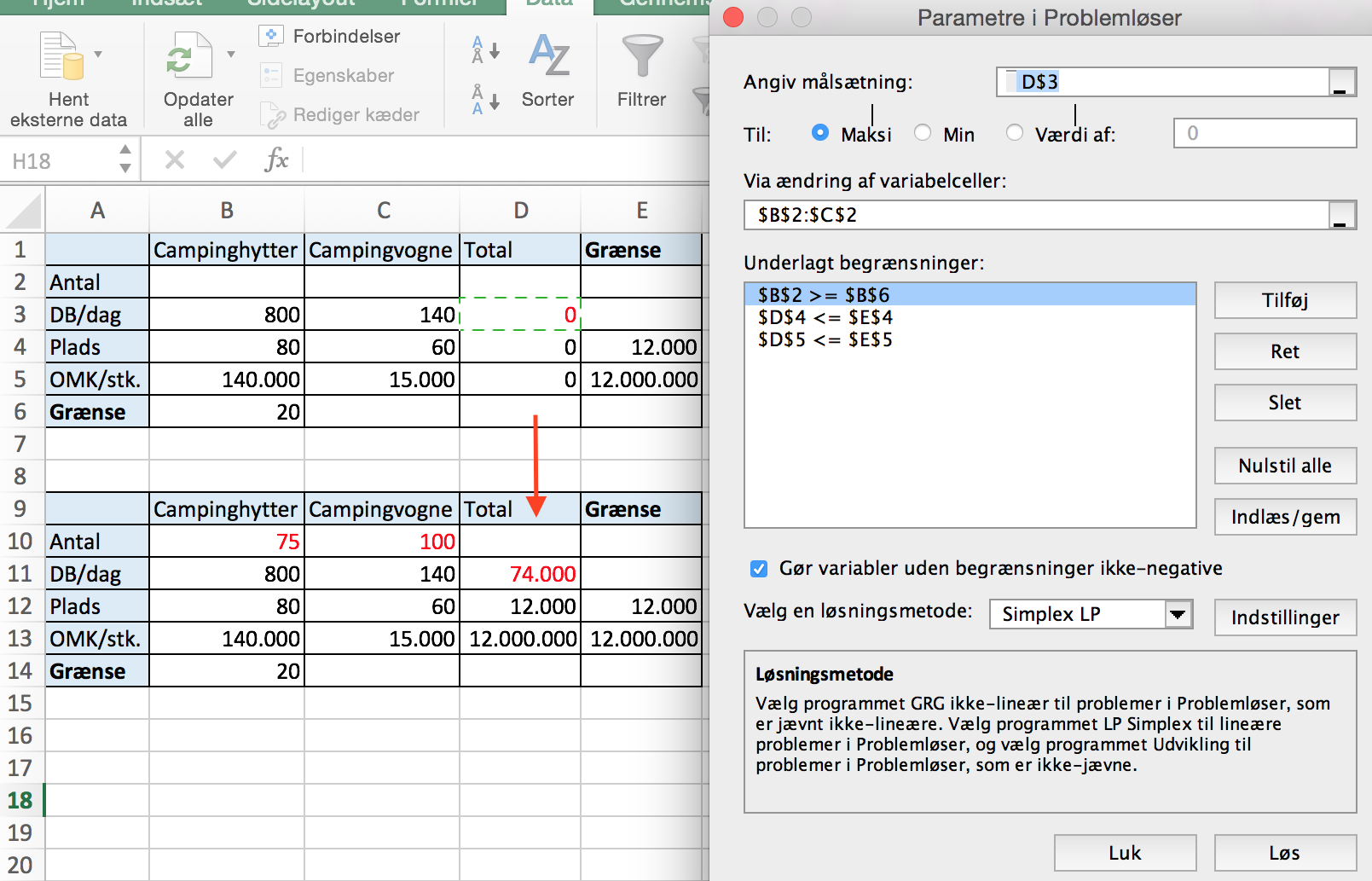
Problemløser installeres med: Funktioner > Excel-tilføjelsesprogrammer > Solver Add In. (Se også Lineær programmering)