Svar på opgave 1:

1. Nedenstående graf er lavet i Excel ved hjælp af fire punkter og diagramfunktionen: XY-plot med udjævnet kurve. Endepunkterne er tilføjet i Mac's tegneprogram.

   

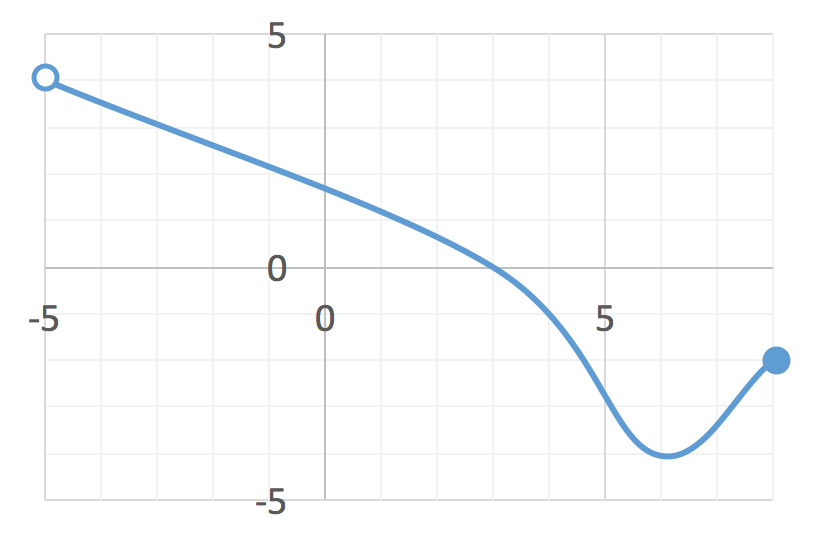
   (Se også: Excel graf.)

Svar på opgave 2:

1. Man ser, at x = -2 er en løsning ved indsættelse.

   Venstre side: (6 + 3x)·(-6x + 24) | Højre side: 0

   Venstre side: (6 + 3·(-2))·(-6·(-2) + 24) | Højre side: 0

   Venstre side: (6 - 6)·(12 + 24) | Højre side: 0

   Venstre side: 0·36 | Højre side: 0

   Venstre side: 0 = Højre side: 0

   Da venstre side er lig med højre side i prøven for ligningen er x = -2 en løsning.

   Den anden løsning findes ved hjælp af nul-reglen:

   (6 + 3x)·(-6x + 24) = 0 ⇔

   6 + 3x = 0 ∨ -6x + 24 = 0 ⇔

   x = -2 ∨ x = 4

   Dvs. den anden løsning er x = 4

Svar på opgave 3:

1. R(x) = 15,7·1,2^x, a = 1 + vækstrate og b = startværdi.

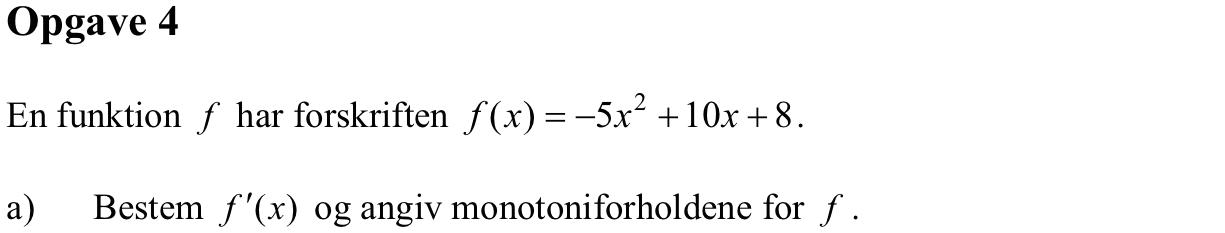
Svar på opgave 4:

1. f´(x) = -10x + 10

   For at finde monotoniforholdene for f(x) laver man en fortegnsundersægelse af f´(x) omkring x = 1:

   f´(0) = 10

   f´(2) = -10

   Dvs. f´(x) > 0 for x < 1 og f´(x) < 0 for x > 1

   Dermed bliver monotoniforholdene:

   f(x) vokser for x mindre end 1 og aftager for x større end 1

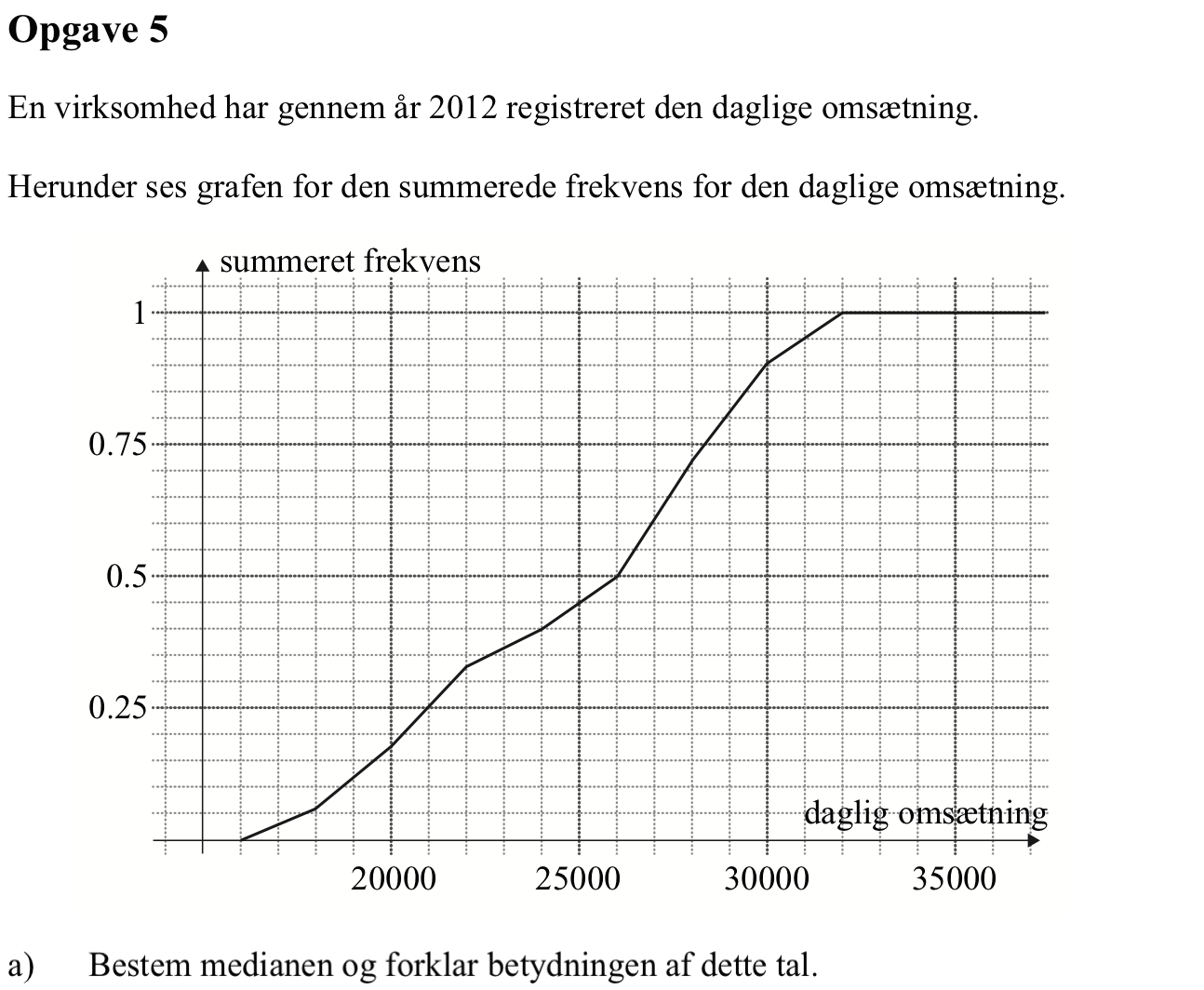
Svar på opgave 5:

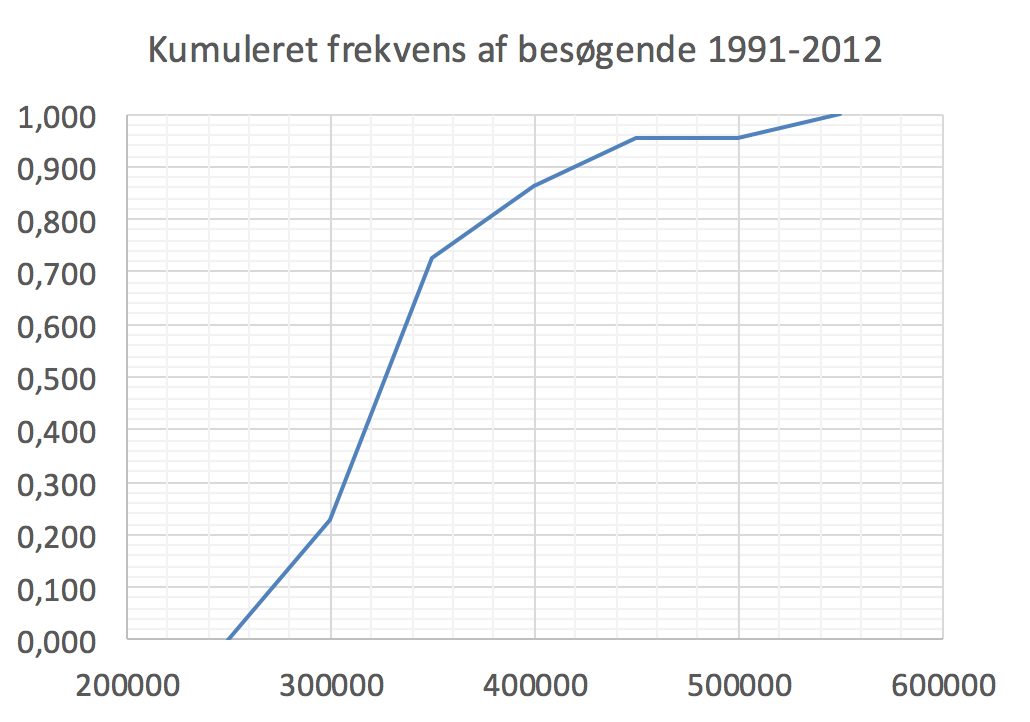
1. Medianen aflæses til 26.000 ved at gå ud fra 0,5 på andenaksen, hen til kurven og ned til første aksen:

   

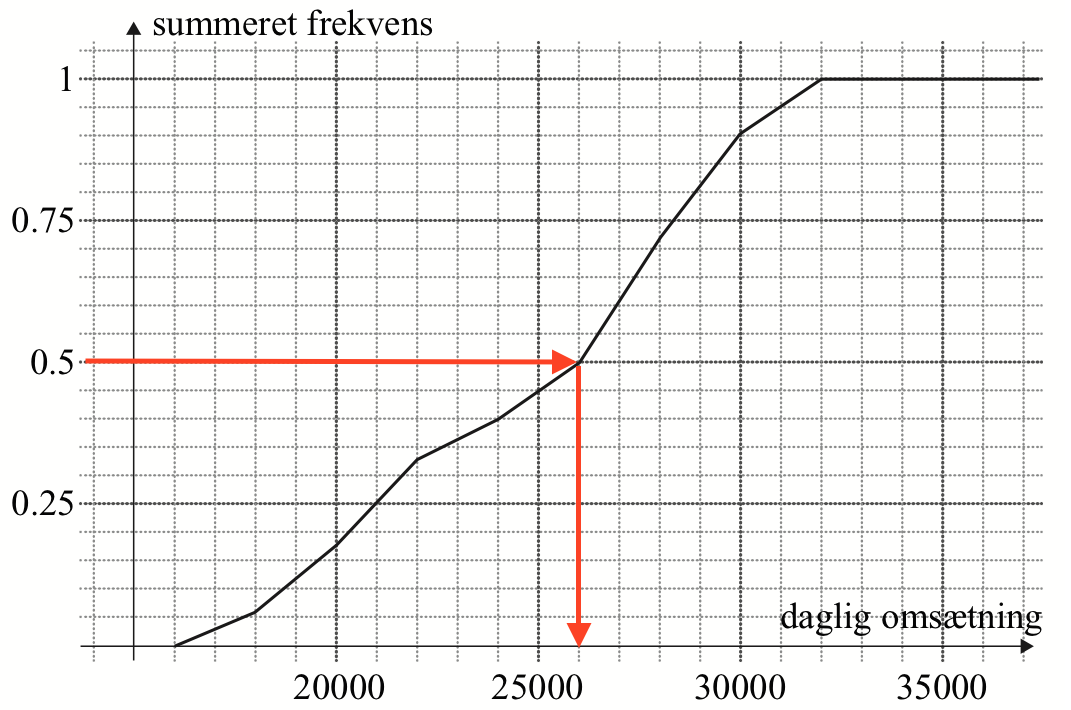
   At medianen er 26.000 betyder, at virksomheden har haft en daglig omsætning på 26.000 eller mindre halvdelen af tiden i 2012.

Svar på opgave 6:

1. solve(100*x^0.6*y^0.4=1000,x) ▸ x=(46.4159)/(y^0.666667)

   Dvs. man får: x = 46.416·y^-0.6667

2. 2. Kvadratleddet på højre side ganges ud

   3. Leddene flyttes over på venstre side, så man har en andengradsligning på standardform

   4. Andengradsligningen løses og man får løsningerne x = 1 og x = 4

Svar på opgave 7:

1. Tabel for observationer

   

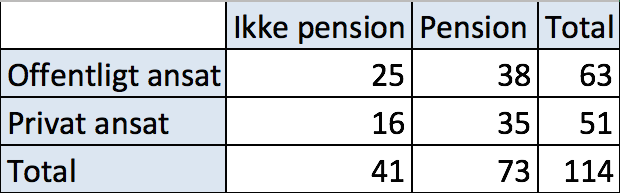
2. Tabeller for observationer og forventede værdier

   

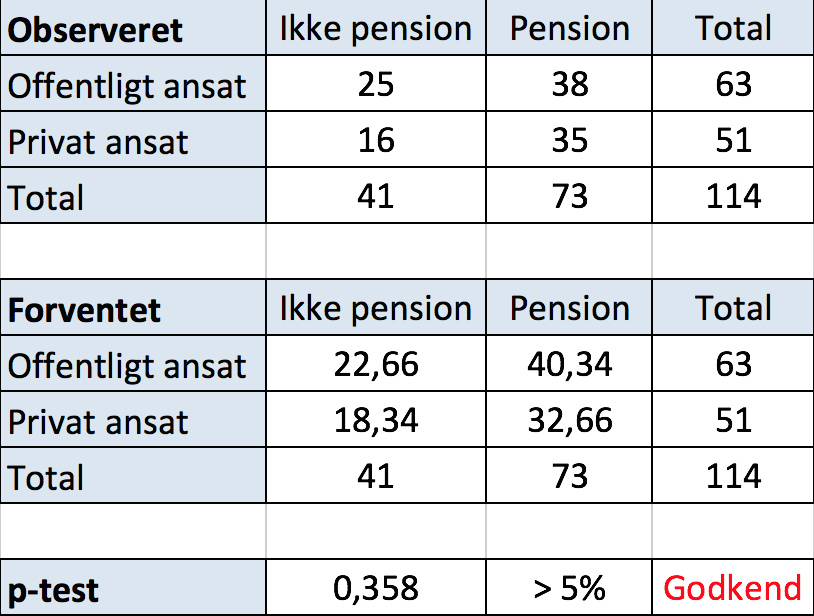
   Ved hjælp af Excel finder man at sandsynligheden for, at afvigelser mellem observerede og forventede værdier kan skyldes tilfældigheder, er 36 % og dermed større end 5 %.

   Dermed godkendes nulhypotesen.

(Se også Excelfilen Pension.)

Svar på opgave 8:

1. Man bruger følgende Ti-Nspire kommandoer:

   r(x):=−x²+502*x ▸ Udført (definer omsætningen)

   fMax(r(x),x) ▸ x=251 (find x, der svarer til maks-værdi)

   r(251) ▸ 63001 (indsæt x og find maks-værdi af omsætning)

   Da x = 251 ligger i definitionsmængden for R(x), får man at maksimalværdien af omsætningen er 63.001 kr.

2. Man bruger følgende Ti-Nspire kommandoer:

   c(x):=50*x ▸ Udført (definer variable omkostninger)

   db(x):=r(x)-c(x) ▸ Udført (definer dækningsbidrag)

   db(x) ▸ 452*x-x² (vis funktionsudtryk for DB(x))

   solve(db(x)>0 and 25≤x≤475,x) ▸ 25≤x<452 (find interval, hvor DB(x) er større end nul)

   Dvs. DB(x) = -x² + 452x og intervallet hvor DB(x) er positivt er 25 ≤ x < 452

Svar på opgave 9:

1. Man bruger formlen for gældsannuitet for at finde rentesatsen pr. termin:

   

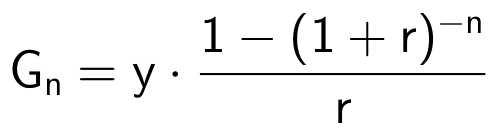
   Dette gøres i Ti-Nspire, hvor rentesatsen kaldes x:

   

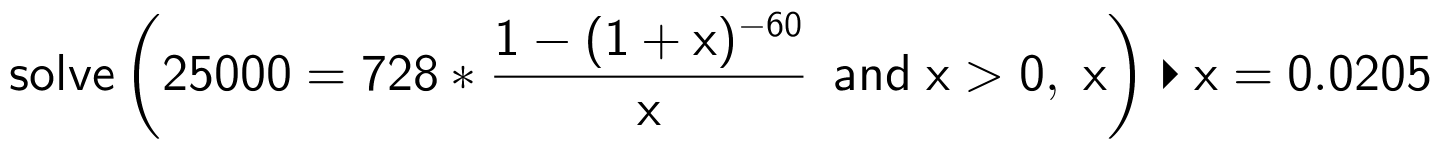
   Det ses at x = 0,0205, og at rentesatsen dermed er 2,05%

   Den årlige effektive rente findes ved hjælp af formlen: r_eff = (1 + r)ⁿ − 1, hvor r = 0,0205 og n = 12. Man får:

   Effektiv årlig rente: (1,0205)¹² − 1 = 0.276 = 28 %

2. L'easy lånets ydelse er mindst, men lånet løber længere.

   L'easy lånet har en samlet rente på 60·728 kr. - 25.000 kr. = 18.680 kr., mens

   Lån & Spar Bank lånet har en samlet rente på 36·967,29 kr. - 25.000 kr. = 9.822,44 kr.

   Det vil sige, at L'easy lånet er billigst i starten (de første 36 måneder), men dyrest i længden.

Svar på opgave 10:

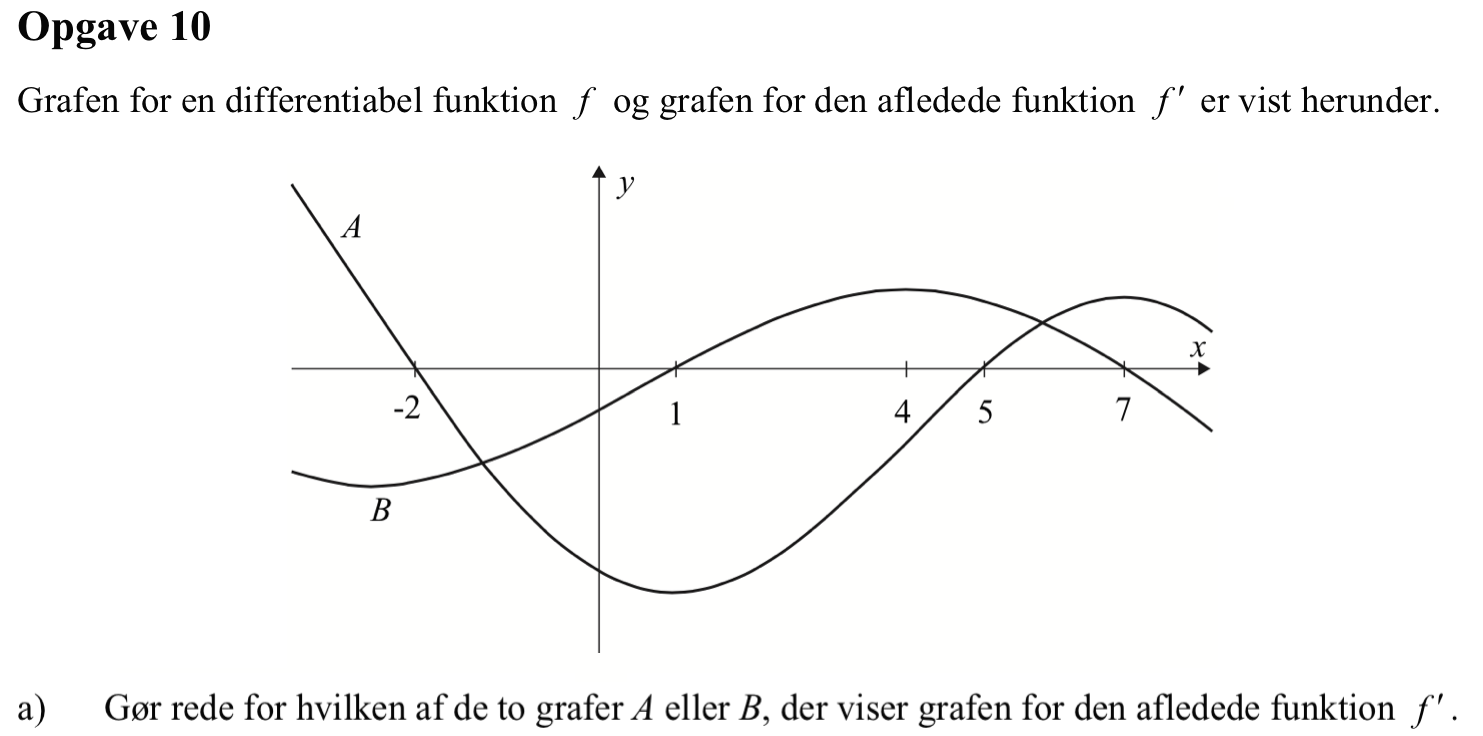
1. A svarer til grafen for f og B svarer til grafen for f´.

   Det ses af, at B skærer x-aksen for de x-værdier, hvor A har lokalt ekstrema (det modsatte er ikke tilfældet).

Svar på opgave 11:

1. Man laver en tendenslinje til plottet i Excel:

   

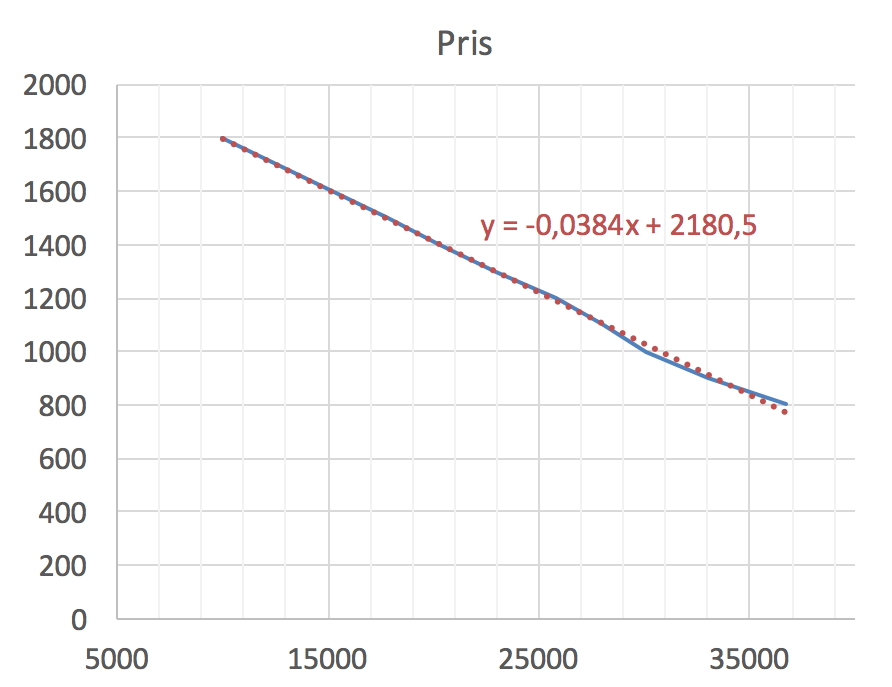
   Det ses at p(x) = -0,0384·x + 2.181

2. Man skal finde det x for hvilket p(x) = 925 kr. Man bruger Ti-Nspire kommandoen:

   solve(−0.0384*x+2180.5=925,x) ▸ x=32695.3

   Dvs. den mængde af varen, der efterspørges ved en pris på 925 kr., er 32.695

(Se også Excelfilen Kunder)

Svar på opgave 12A:

1. Man skal bruge en binomialfordeling, hvor p = 0,05 (5%) og N = 1500. Forventningsværdien er p·N = 0,05·1500 = 75

2. Man bruger følgende kommando i Ti-Nspire:

   binomCdf(1500,0.05,0,65) → 0.1290

   Dvs. sandsynlignheden for, at der højst er 65 defekte, er 0,129

Svar på opgave 12B:

1. Man laver en sumkurve i Excel:

   

2. Beregnet i Excel:

   Middel = 341,4

   Median 330,3

   90%-fraktil 420,4

(Se også Excel-filen Eksperimentarium.)

Svar på opgave 12C:

1. Forskriften er f(x,y) = 15x + 20y, hvor x er antal kg oksekød og y er antal kg lammekød.

2. Ud fra begrænsningerne tegner man polygonområdet som vist med mørkblå på nedenstående tegning lavet i Geogebra.

   

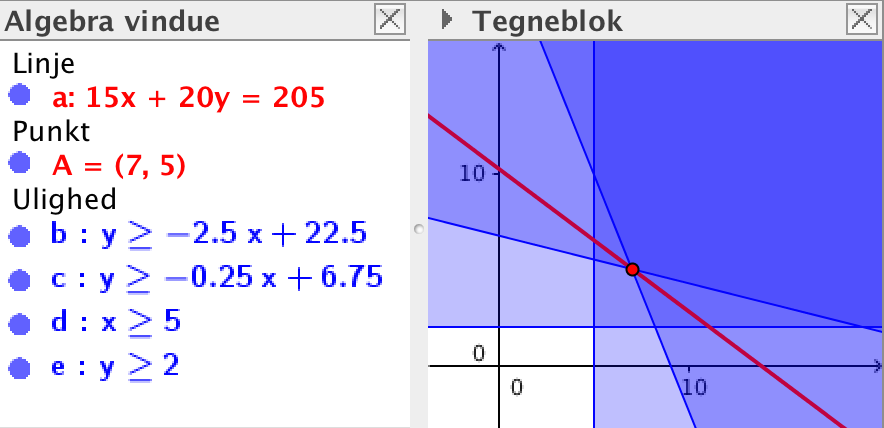
   Den niveaukurve, der giver den laveste værdi, er tegnet med rødt.

   Minimumpunktet er (7,5), dvs. 7 kg. oksekød og 5 kg. lammekød

   Minimumværdien for de daglige omkostninger er f(x.y) = 205 kr.

Løsning med Excel Problemløser:

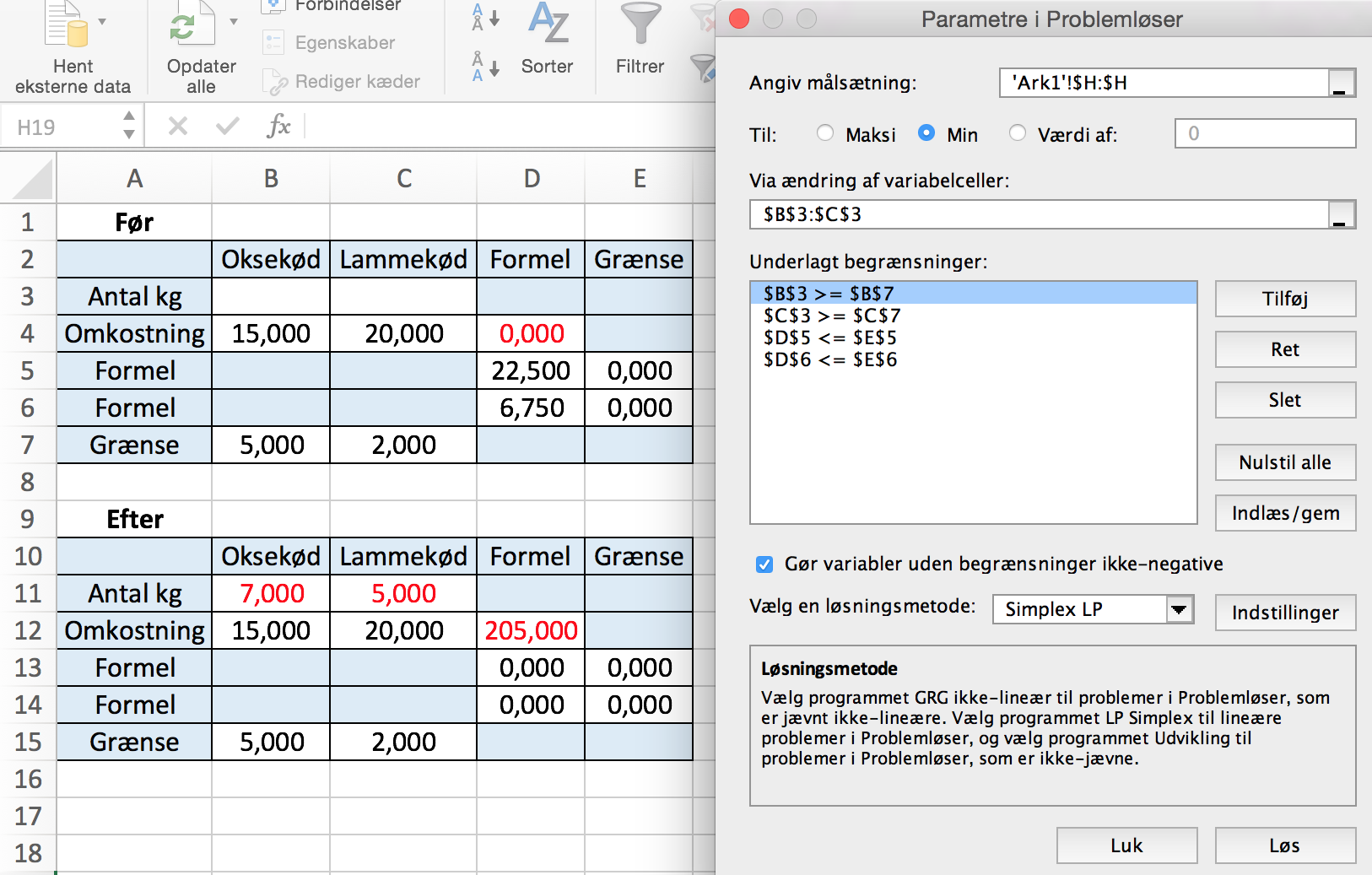
Problemløser installeres med: Funktioner > Excel-tilføjelsesprogrammer > Solver Add In. (Se også Excelfilen Lineær programmering)