Svar på opgave 1:

1. Man vælger værdien 100.000 kr. på y-aksen og den halve værdi 50.000 kr. De svarer til henholdsvis 3,2 år og 5,2 år på x-aksen som vist med de røde pile.

   

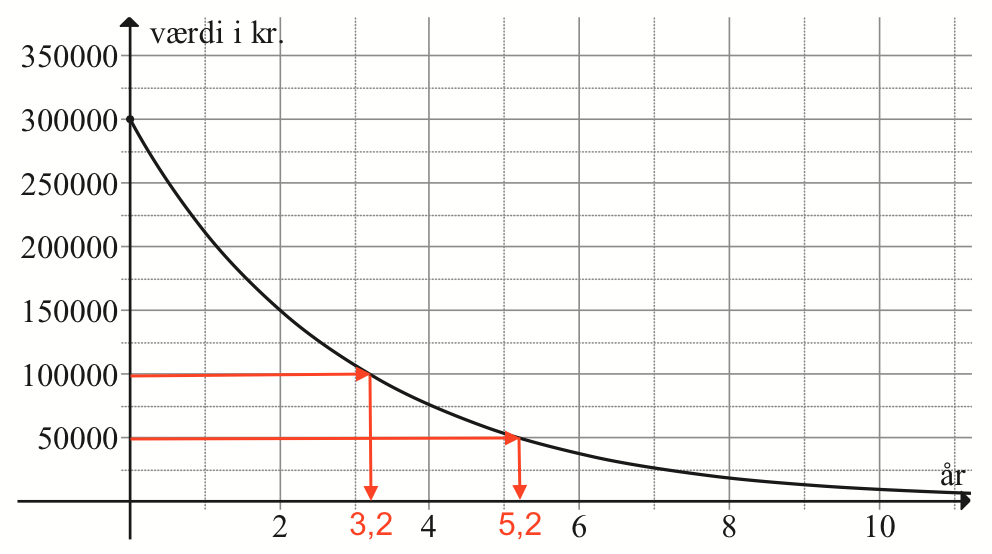
   Forskellen mellem disse er 2 år, dvs. halveringstiden er 2 år

Svar på opgave 2:

1. f´(x) = x - 8.

   Man skal undersøge om f´(4) = 0 og om f´(x) skifter fortegn, når x passerer 4.

   f´(4) = 4 - 8 = -4, som er forskelligt fra 0. Dermed har f(x) ikke ekstremum i x = 4.

Svar på opgave 3:

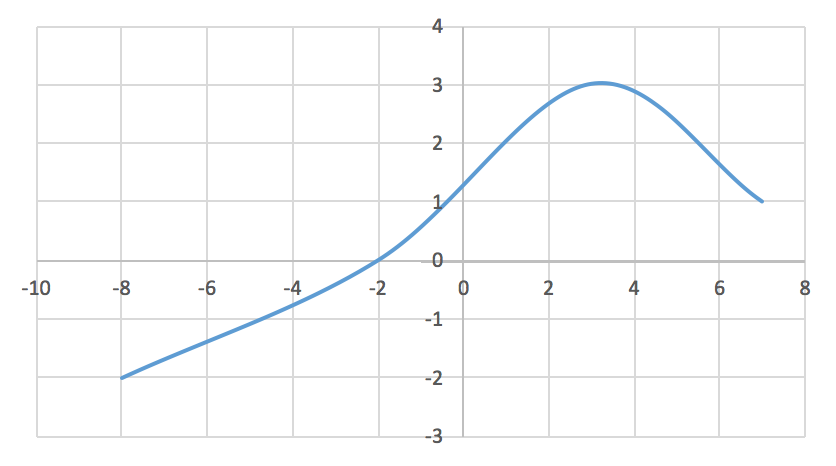
1. Nedenstående graf er tegnet i Excel:

   

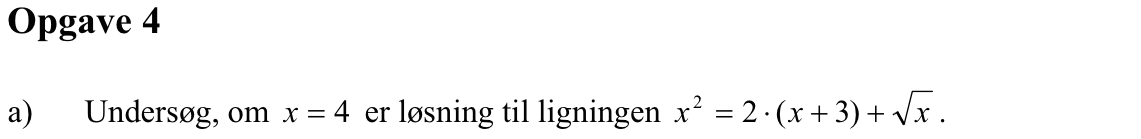
Svar på opgave 4:

1. Man skal gøre prøve og se om venstre og højre side af ligningen giver det samme, når man indsætter x = 4.

   Venstre: 4² = 16

   Højre side: 2·(4 + 3) + √4 = 2·7 + 2 = 16

   Da venstre og højre side giver det samme, vil det sige, at x = 4 er en løsning til ligningen.

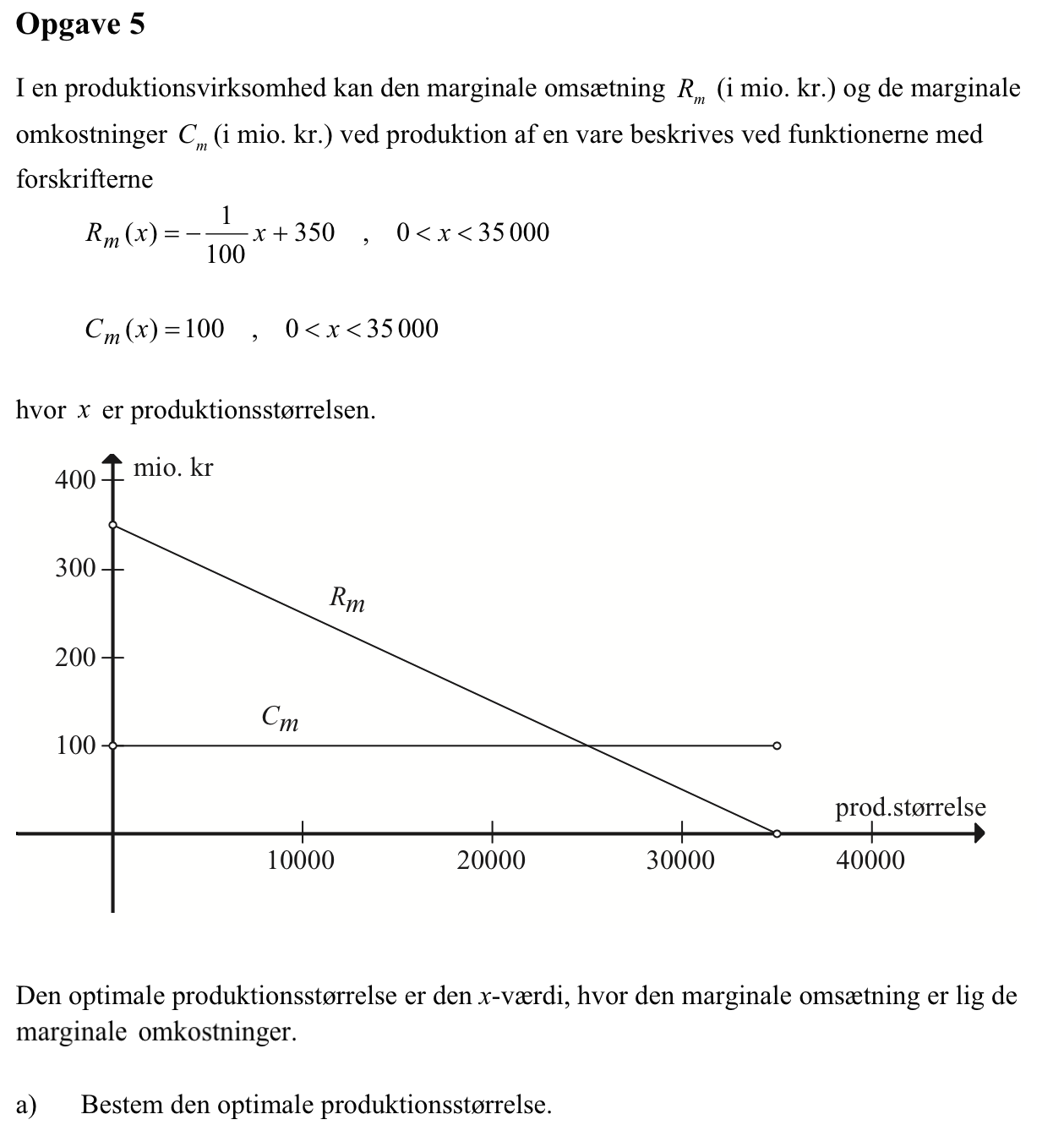
Svar på opgave 5:

1. Man skal løse ligningen R_m(x) = C_m(x) med hensyn til x. Man får:

   (-1/100)·x + 350 = 100 ⇒

   (-1/100)·x = 100 - 350 ⇒

   x = -250·(-100) ⇒

   x = 25000

   Dvs. den optimale produktionsstørrelse er 25.000 stk.

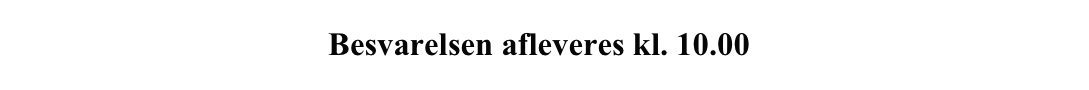
Svar på opgave 6:

1. Man løser ligningen med solve()-kommandoen i Ti-Nspire:

   solve(m^−0.75*(800-(2/5)*m)^0.25=0,m) ▸ m=2000.

   Dvs. løsningen er m = 2000

2. Man får:

   

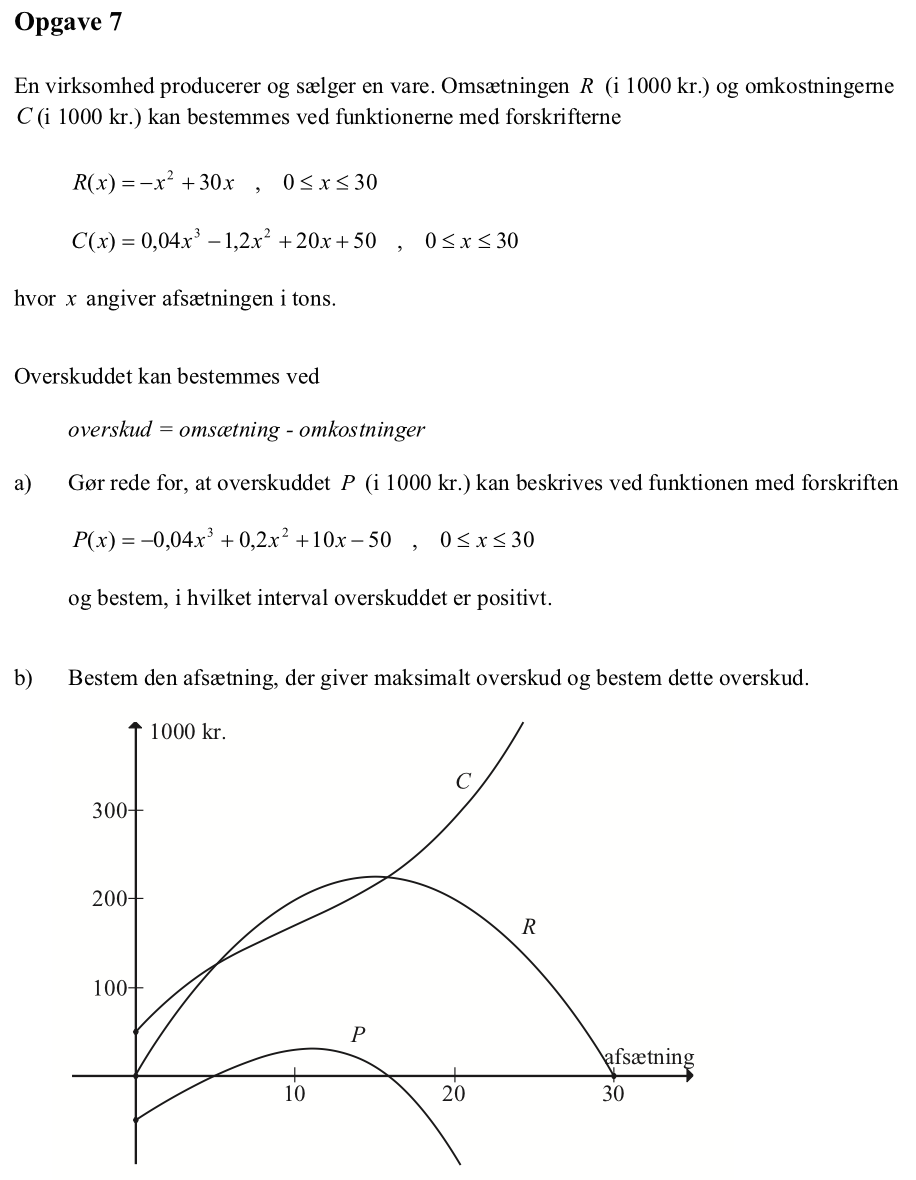
Svar på opgave 7:

Man opretter funktionerne R(x), C(x) og P(x) i Ti-Nspire:

1. r(x):=−x^(2)+30*x ▸ Udført

   c(x):=0.04*x^(3)-1.2*x^(2)+20*x+50 ▸ Udført

   p(x):=r(x)-c(x) ▸ Udført

   Man udskriver funktionsudtrykket for P(x):

   p(x) ▸ −0.04*x³+0.2*x²+10*x-50

   hvilket viser, at funktionsudtrykket er som angivet.

   Man finder intervallet af x-værdier, hvor P(x) er positiv med solve-kommandoen i Ti-Nspire:

   solve(p(x)>0,x)|0≤x≤30 ▸ 5.<x<15.811

   Dvs. overskuddet er positivt for 5 tons < x < 15,81 tons

2. Man bruger fMax-kommandoen i Ti-Nspire for at finde den x-værdi, som giver højeste overskud:

   fMax(p(x),x)|0≤x≤30 ▸ x=10.946

   Dvs. den afsætning, der giver størst overskud, er 10,9 tons

   Denne værdi indsættes i P(x) for at finde det største overskud:

   p(10.946) ▸ 30.963

   Dvs. det største overskud er 30963 kr.

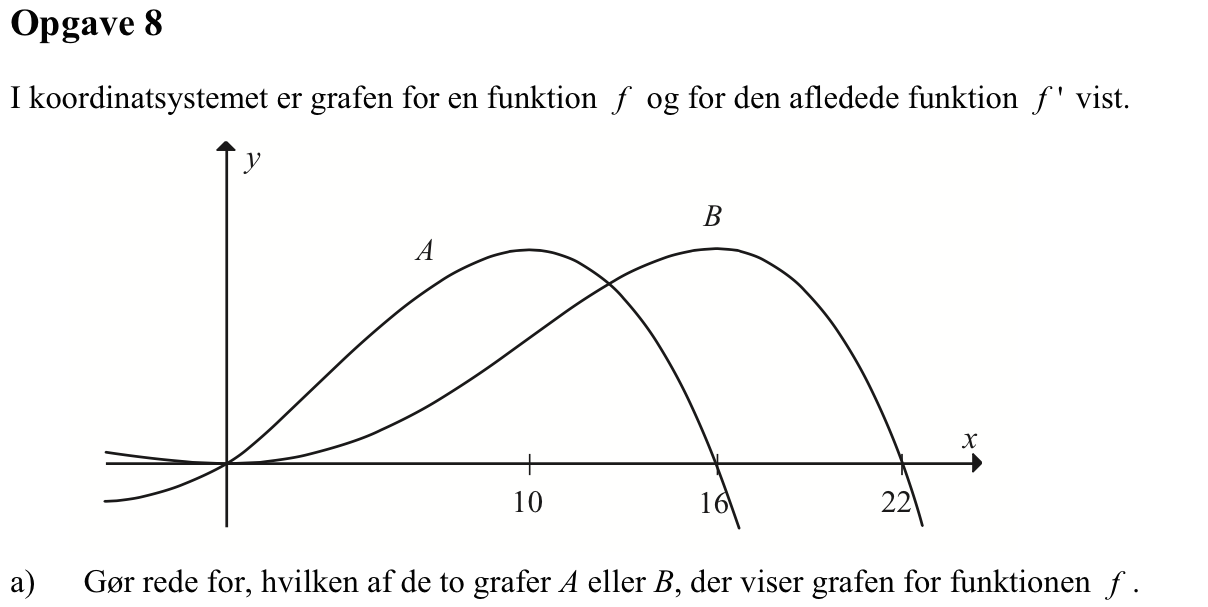
Svar på opgave 8:

1. A er grafen for f´ da den har nulpunkter for de x-værdier, hvor B har ekstrema. B er dermed graf for f.

Svar på opgave 9:

1. Nedenunder er tegnet en sumkurve for frekvenserne af ostenes vægt, når man inddeler vægtene i de intervaller, der står på førsteaksen.

   Intervallerne er fundet ved at sortere tallene for at finde det største og det mindste. Det mindste tal 765 rundes ned til nærmeste antal 10. Det højeste er 830 og afrundes ikke. Forskellen på 760 og 830 er 70, som deles i 7 intervaller med en længde på 10.

   

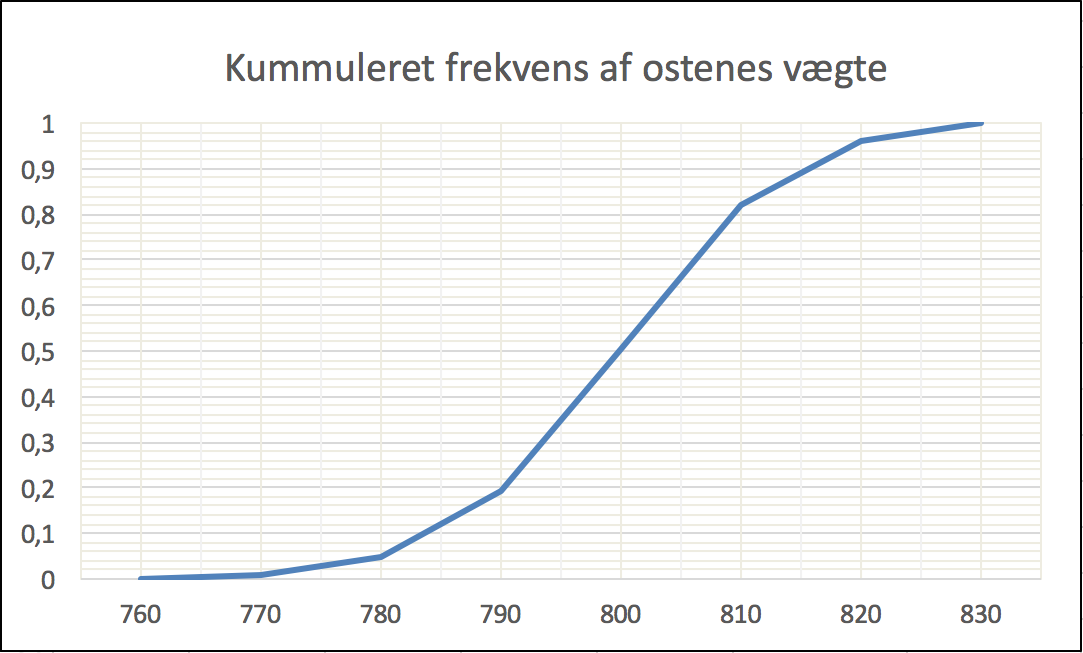
   Man bruger kommandoen =TÆL.HVIS(A:A;">" & C2)-TÆL.HVIS(A:A;">" & D2) for at finde hyppigheden af oste i hvert vægt-interval. Den tæller antallet af celler i A-søjlen, der indeholder et tal, der er større end det som står i celle C2 (nedre grænse for interval). Fra dette tal trækkes antallet celler, der indeholder et tal, der er større end D2 (øvre grænse for interval).

2. 25 %-fraktilen beregnes med Excel-kommandoen =KVARTIL(A2:A151;1) til 792

   Middelværdien beregnes med Excel-kommandoen =MIDDEL(A2:A152) til 800,2

   Medianen beregnes med Excel-kommandoen =KVARTIL(A2:A151;2) til 800

3. Sansynligheden findes ved hjælp af Excel-kommandoen =NORMAL.FORDELING(780;800;12;SAND) der giver P(X<780) = 0,048

4. Ostenes vægt er i gennemsnit 800 g, ingen vejer under 765 g eller over 830 g. 25 % af ostene vejer under 792 g.

(Se også Excelfilen Ost.)

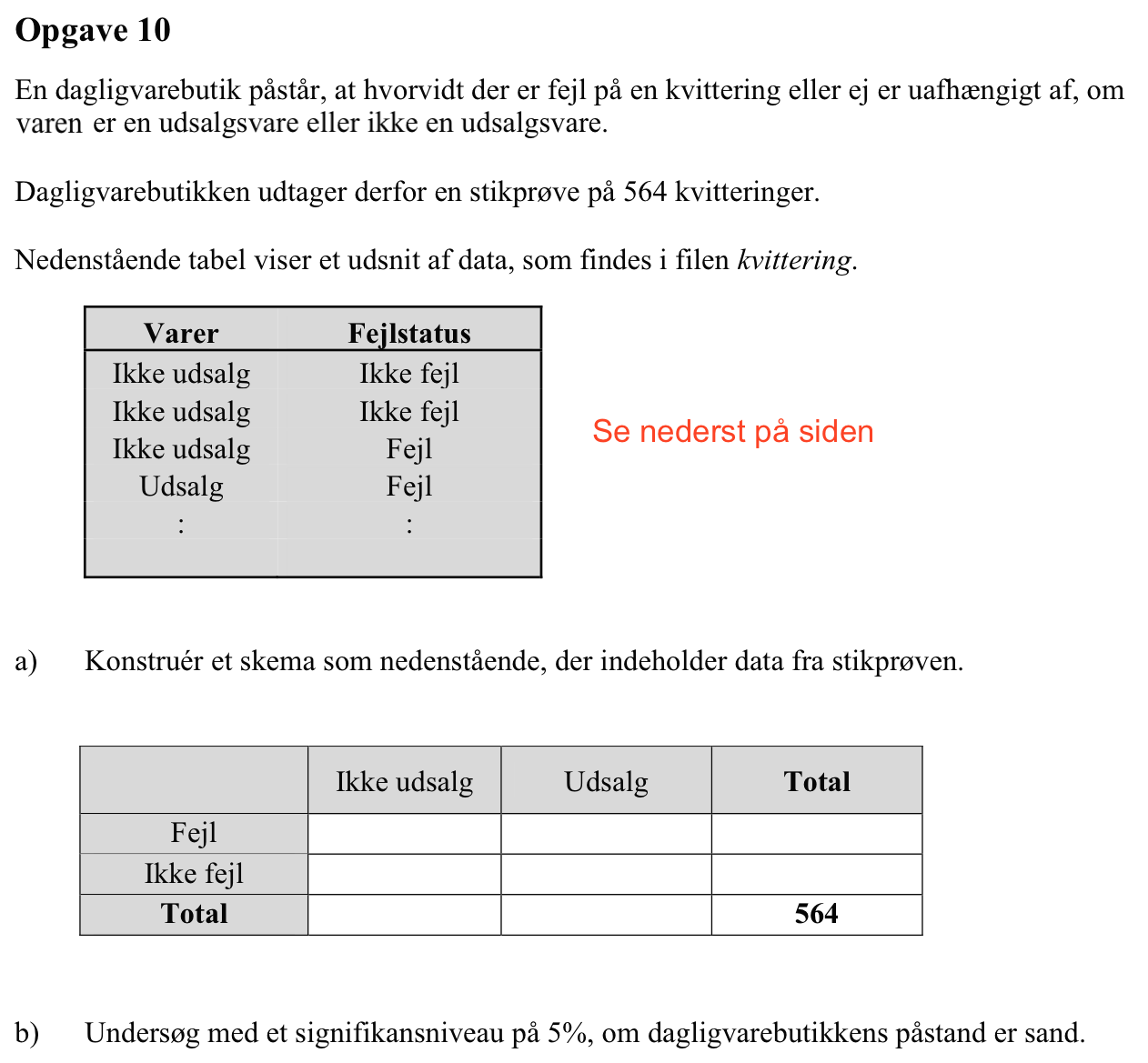
Svar på opgave 10:

1. Svaret på a) er er fundet i Excel og vist i den øverste tabel ("Observeret") på billedet nedenunder:

   

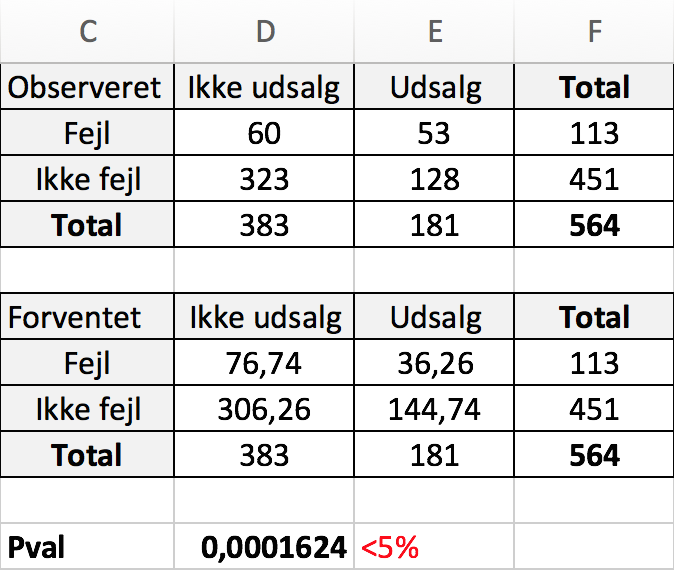
   I tabellen er brugt kommandoen =TÆL.HVISER($A:$A;D$1;$B:$B;$C2), der finder antallet af kombinerede forekomster af overskriften for oven og overskriften til venstre for cellen i de to kolonner med data A og B.

2. Man skal lave en chi-i-anden uafhængighedstest. For at gøre det i Excel, laves først tallet mærket "Forventet" som vist ovenfor.

   Her er brugt Excel-kommandoen =$F2*D$4/$F$4, der for hver celle i tabellen med forventede værdier tager den tilsvarende celle i tabellen med observerede værdier og ganger side- med bund-total for derefter at dividere med det samlede antal oberservationer.

   Nulhypotesen er, at fejl på kvitteringen er uafhængig af om varen er på udsalg eller ej.

   En chi-i-anden uafhængighedstest i Excel laves med formlen =CHI2.TEST(D2:E3;D7:E8), hvor D2:E3 er tabellen med observerede værdier og D7:E8 er tabellen med forventede værdier.

   Chi-i-anden testens resultat er en sandsynlighed, der på billedet ovenfor kaldes "PVal" og er lig 0,000162. Da denne værdi er mindre end 5% (0,05) forkastes nulhypotesen, dvs. dagligvarebutikkens påstand er forkert

(Se også Excelfilen Kvittering.)

Svar på opgave 11a:

1. xy-plottet af pris (y) som funktion af afsætnng (x) er vist nedenunder (lavet i Excel):

   

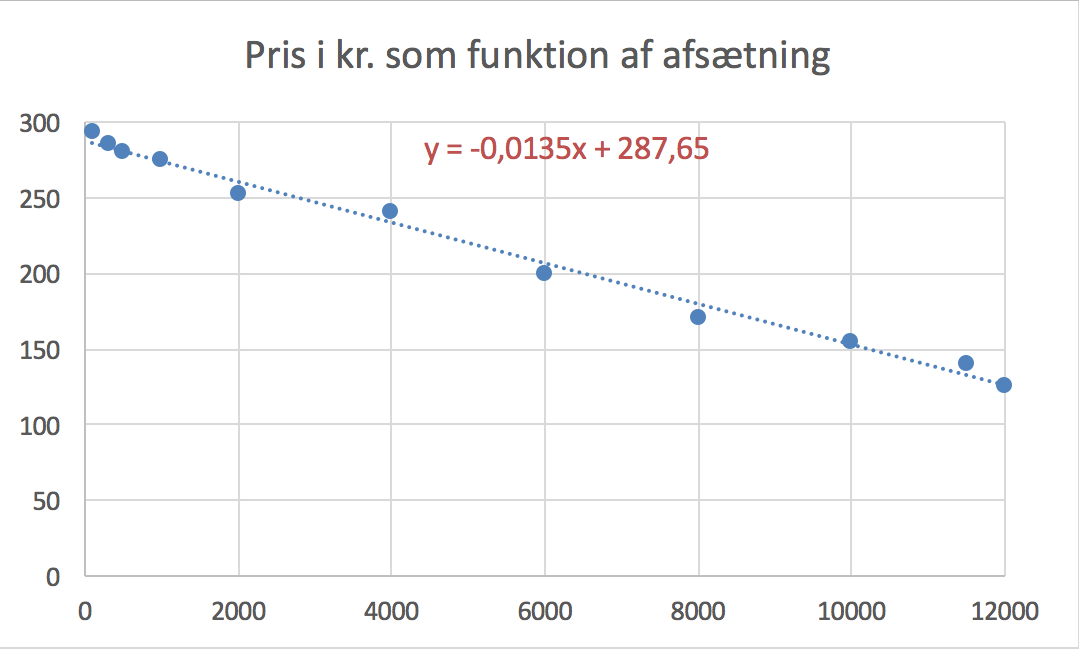
   Regressions-kurven er fundet som en lineær tendenskurve i Excel. Den er y = -0,0135x + 287,65

2. Ved hjælp af regressionsformlen får man følgende ligning, som skal løses med hensyn til x: 150 = -0,0135·x + 287,65 ⇒ x = 10200

   Dvs. en pris på 150 kr. giver en afsætning på 10200 stk.

(Se også Excelfilen Pris-afsætning.)

Svar på opgave 11b:

1. Man laver en amortisationstabel i Excel:

   

   ...

   

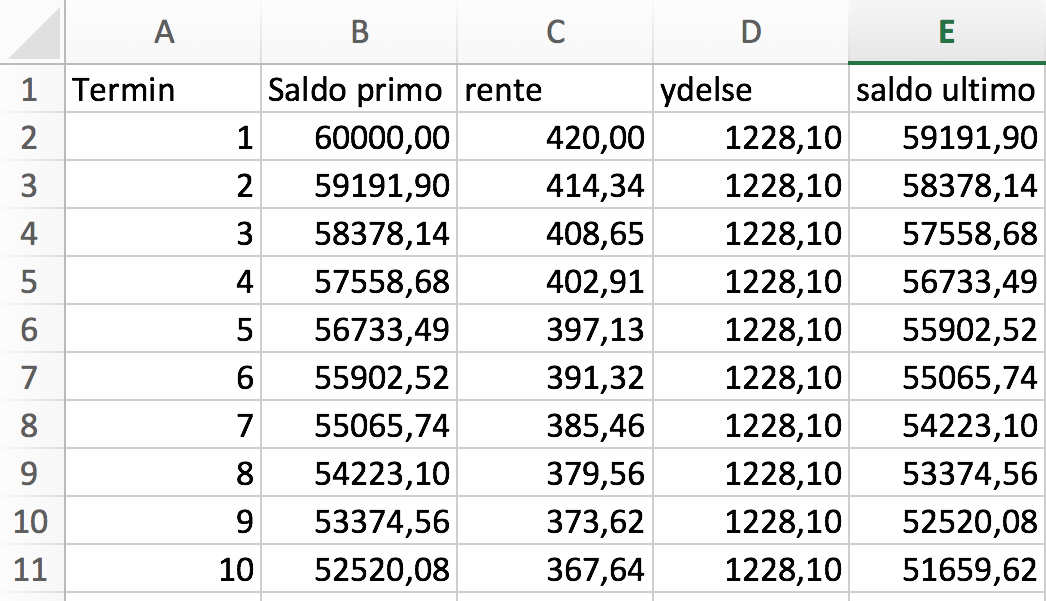
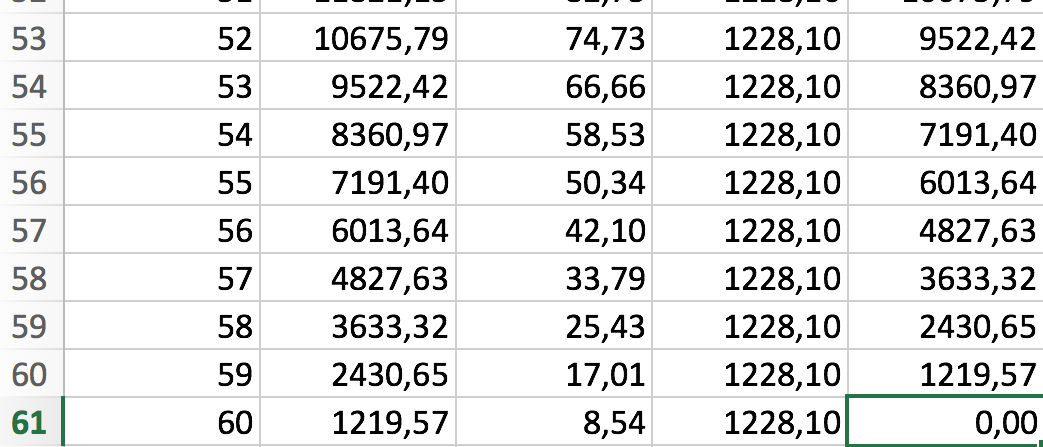
   Ydelsen findes ved hjælp af målsøgning i Excel (Funktioner - målsøgning). Man vælger cellen E61 som målet, der skal give o, når indholdet af D2 (ydelsen) ændres. Resultatet er ydelsen 1228,10 kr.

2. Man laver en amortisationstabel med de nye oplysninger i Excel:

   

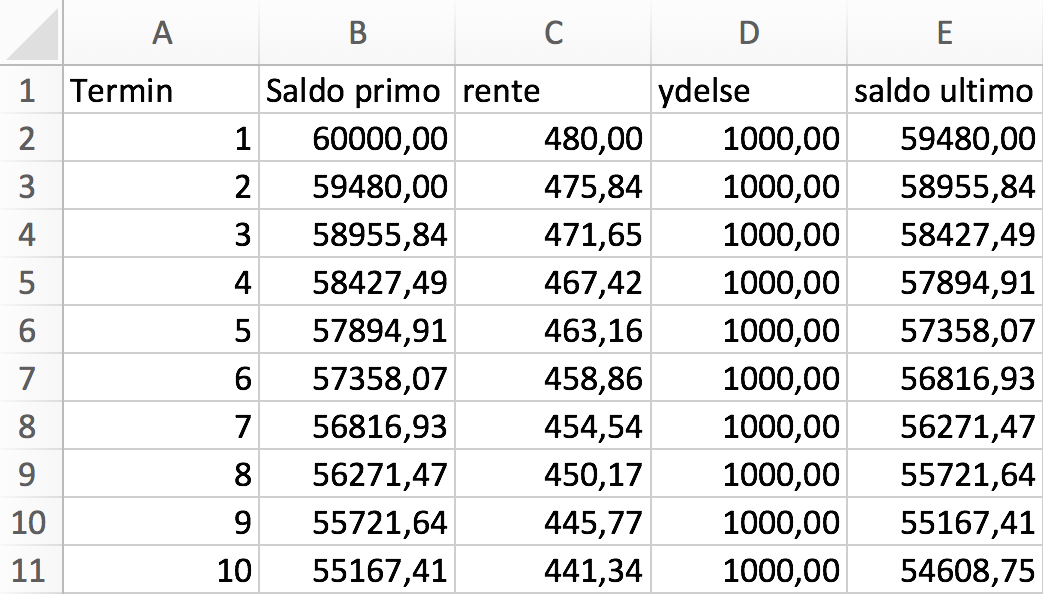
   ... formlerne i anden række (B:2 til E:2) trækkes nedad indtil saldo ultimo bliver negativ...

   

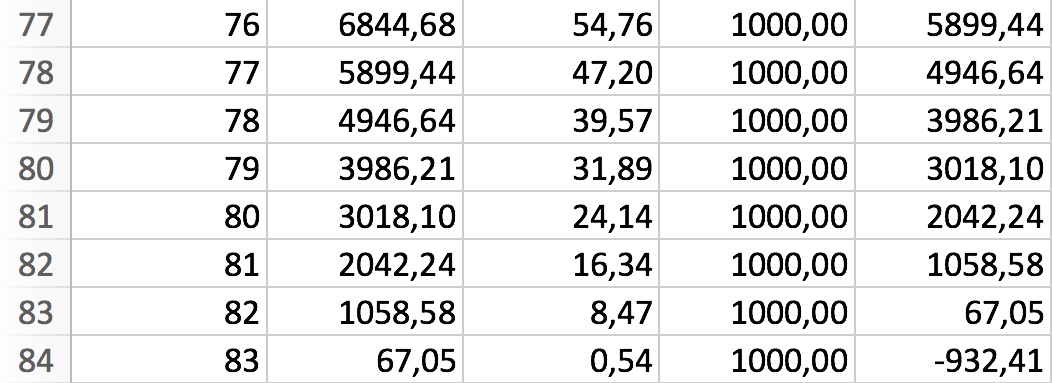
   Det ses at ske efter 83 terminer, dvs. der er 83 ydelser

(Se også Excelfilen Ydelse 11b.)

Svar på opgave 11c:

1. f(x,y) = 10x + 15y

   Nedenunder er polygon-området tegnet i Geogebra.

   

2. Optimummet findes i Excel ved hjælp af problemløser.

   

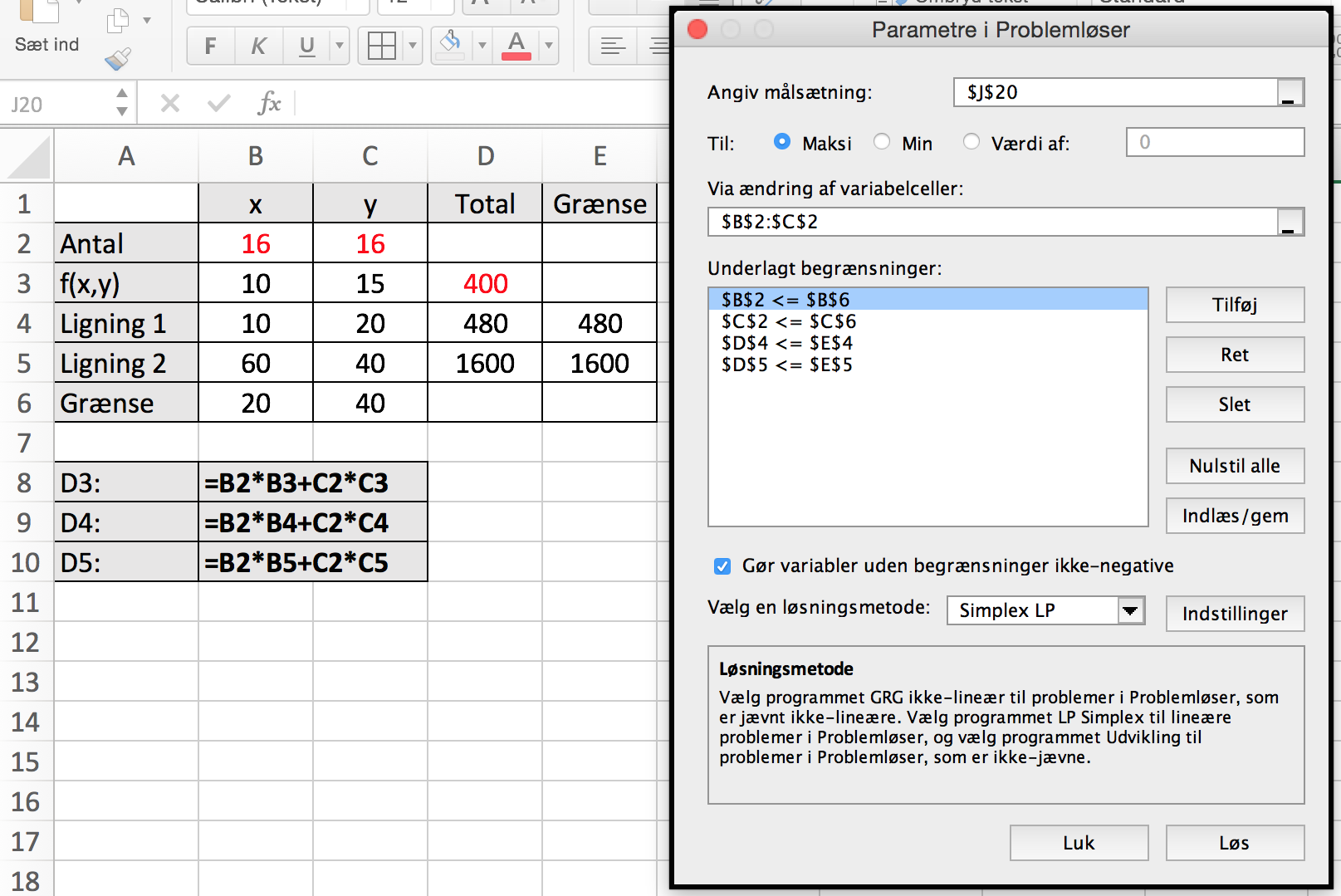
   De grå felter under tabellen viser hvilke formler, der er brugt i cellerne D3, D4 og D5. D3 er beregningen af dækningsbidraget.

   Problemløser installeres med: Funktioner < Excel-tilføjelsesprogrammer > Solver Add In. Formlerne, der er benyttet, kan ses i Excel-filen "Lineær programmering" i bunden

   Største dækningsbidrag fås for 16 af hvert produkt

   Største dækningsbidrag er 400 kr. pr. dag

   (Se også Excelfilen Lineær programmering.)

   Grafisk løsning i Geogebra:

   

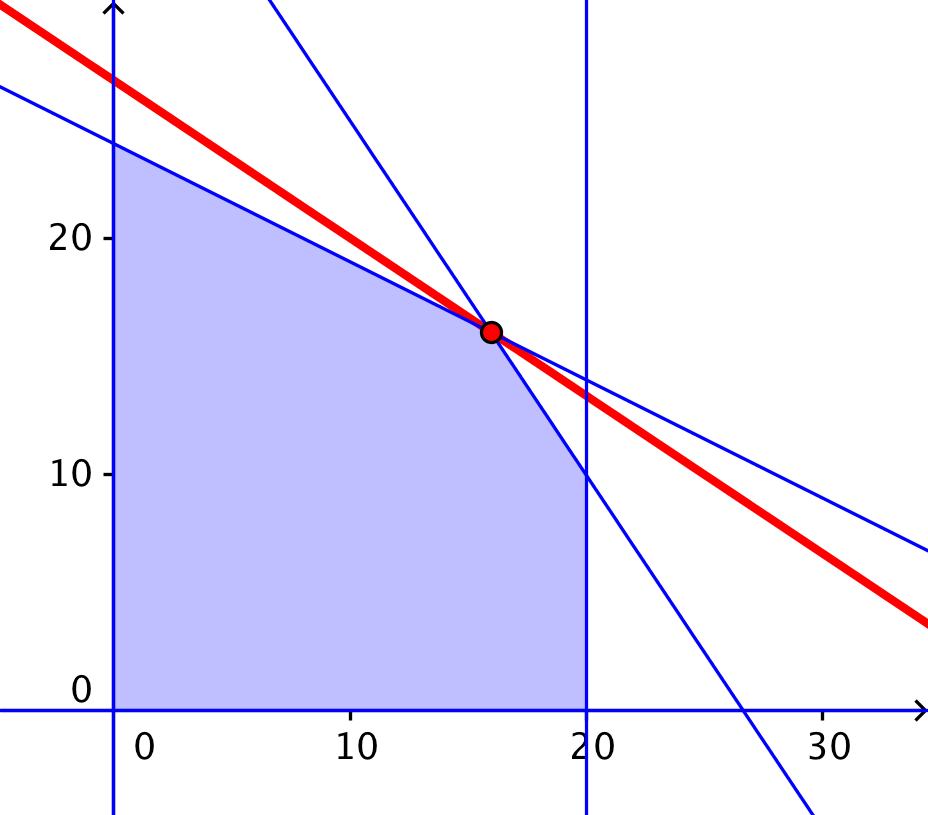
   Man parallelforskyder linjen 10x + 15y = 0 så langt væk fra (0,0) som muligt til den er lige ved at miste kontakten med polygonområdet. Det sker når linjen går gennem (x,y) = (16,16) som vist.

   Dvs. optimummet fås for 16 af hvert produk som ovenfor og det største dækningsbidrag beregnes ligeledes til 16·10 + 16·15 kr. pr. dag = 400 kr. pr. dag.